
2. Простейшие способы интегрирования.
а) Непосредственное интегрирование.
Нахождение интегралов функций, основанное на прямом применении свойств неопределенных интегралов и таблицы основных формул интегрирования. Рассмотрим пример нахождения интеграла функции путем непосредственного интегрирования.
Пример:
∫(х–3)2dх= ∫(х2–6х+9)dх= ∫х2dх- 6∫хdх+9∫dх= х3∕3 -3 х2+9х+С.
В подавляющем большинстве случаев мы имеем дело с интегралами функций, которые нельзя найти непосредственным интегрированием. В этом случае необходимо сделать подстановку (заменить переменную).
б) Интегрирование подстановкой (замена переменной).
Интегрирование подстановкой, или как его часто называют, методом замены переменой, является одним из более эффективных и распространенных методов интегрирования. Способ подстановки состоит в том, чтобы перейти от данной переменной интегрирования к другой переменной с целью упростить подинтегральное выражение и привести его к одному из табличных видов интегралов. При этом выбор подстановки решается исполнителем индивидуально, т.к. не существует общих правил, указывающих какую подстановку в данном случае взять.
Пример:Найти интеграл ∫е2х+3dх.
Введем новую переменную t, связанную сх следующей зависимостью 2х+ 3 =t.
Возьмем дифференциалы от левой и правой частей этого равенства: 2dх=dt;dх=dt/2.
Теперь вместо
2х+ 3 иdх в
подинтегральное выражение подставим
их значения. Тогда получим: ∫е2х+3dх=![]() ∫еtdt=
∫еtdt=![]() еt + С.
Возвращаясь к прежней переменной,
получим окончательно выражение:
еt + С.
Возвращаясь к прежней переменной,
получим окончательно выражение:
∫е2х+3dх=![]() е2х+3 + С.
е2х+3 + С.
Чтобы убедиться
в правильности взятия интеграла
необходимо первообразную функцию
![]() е2х+3 продифференцировать
и проверить, будет ли ее производная
равна подинтегральной функции:
е2х+3 продифференцировать
и проверить, будет ли ее производная
равна подинтегральной функции:
(![]() е2х+3)' =
е2х+3)' =![]() е2х+3 · (2х+3)' =е2х+3.
е2х+3 · (2х+3)' =е2х+3.
3. Определенный интеграл и его свойства.
Понятие определенного интеграла широко используется во многих областях науки и техники. С его помощью вычисляются площади, ограниченные кривыми, объемы произвольной формы, мощность и работа переменной силы, путь движущегося тела, моменты инерции и многие другие величины.
В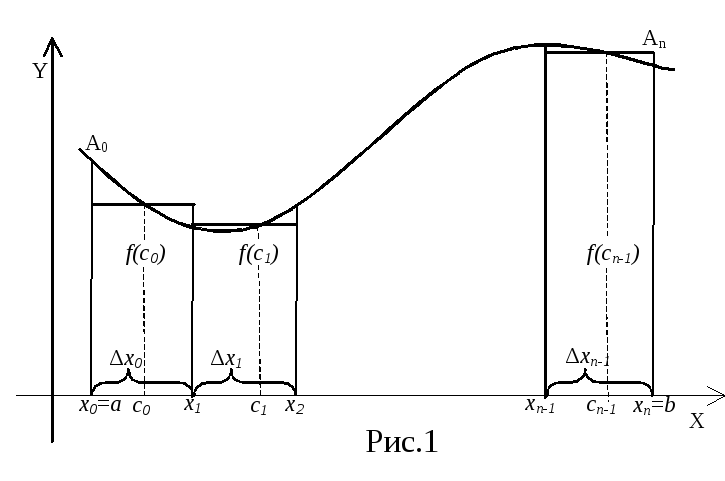 подавляющем большинстве случаев понятие
определенного интеграла вводится при
решении задач определения площади
криволинейной трапеции. Пусть имеется
непрерывная функция у =f(х)
на отрезке [а,в]. Фигуру, ограниченную
кривой у=f(х) ординатамиаАо , вАпи
отрезком [а,в] оси абсцисс называют
криволинейной трапецией (рис.1).
подавляющем большинстве случаев понятие
определенного интеграла вводится при
решении задач определения площади
криволинейной трапеции. Пусть имеется
непрерывная функция у =f(х)
на отрезке [а,в]. Фигуру, ограниченную
кривой у=f(х) ординатамиаАо , вАпи
отрезком [а,в] оси абсцисс называют
криволинейной трапецией (рис.1).
Поставим перед собой задачу: определить площадь Sкриволинейной трапецииаАоАпв. Для этого разобьем отрезок [а,в] напне обязательно равных частей и обозначим точки деления таким образом:а =хо‹х1‹х2 ‹ … ‹хп = в .
Из точек деления восстановим перпендикуляры до пересечения с кривой у = f(х). Таким образом, мы всю площадь, ограниченную кривой, разбили напэлементарных криволинейных трапеций. Восстановим из произвольных точек каждого отрезка ∆хiординатыf(Сi) до пересечения с кривой у =f(х). Далее построим ступенчатую фигуру, состоящую из прямоугольников с основанием ∆хi и высотой f(Сi). Элементарная площадьi-го прямоугольника будетSi =f(Сi)(хi -хi-1), а вся площадьSпполученной ступенчатой фигуры будет равна сумме площадей прямоугольников:
Sп= f(Со)(х1
–хо) +f(С1)(х2
–х1 ) + … +f(Сп-1)(хп
–хп-1).
f(Со)(х1
–хо) +f(С1)(х2
–х1 ) + … +f(Сп-1)(хп
–хп-1).
Для
сокращения записи этой суммы вводят
символ
![]() (сигма)
– знак, означающий суммирование величин.
Тогда
(сигма)
– знак, означающий суммирование величин.
Тогда
Sп
=![]() .
.
Эта
сумма Sп , которая
называется интегральной суммой, может
быть или больше или меньше истинного
значения данной площади. Наиболее
близким значением к истинной величине
площади будет предел суммы при условии,
что элементарные отрезки будут дробиться
(п→![]() ), а длина самого большого отрезка ∆хmaxбудет стремиться к нулю, т.е.:
), а длина самого большого отрезка ∆хmaxбудет стремиться к нулю, т.е.:
S=
![]() (4)
(4)
Этот
предел интегральной суммы (если он
существует) называется определенным
интеграломот функцииf(х)
на отрезке [а,в] и обозначают:![]() =
=
![]() (5)
(5)
(читается – “определенный интеграл от адовэф от икс дэ икс”).
Числа аив называются соответственно нижним и верхним пределами интегрирования,f(х) – подинтегральной функцией;х– переменной интегрирования. Применив формулы (4) и (5) можно записать. Что площадь криволинейной трапеции численно равна интегралу от функции, ограничивающей трапецию, взятому на интервале интегрирования [а,в]:
![]() .
.
Этот факт выражает геометрический смысл определенного интеграла.
Рассмотрим свойства определенного интеграла.
1. Определенный интеграл
не зависит от обозначения переменной,
т.е.:
![]() =
=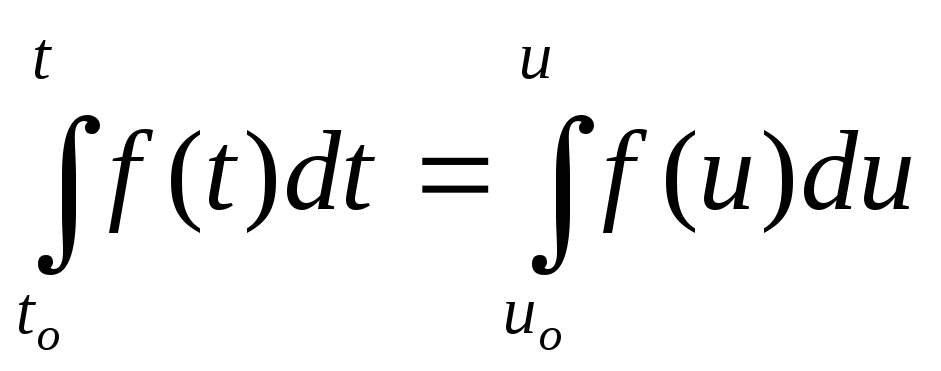 .
.
2. Определенный интеграл алгебраической суммы равен алгебраической сумме определенных интегралов от каждого слагаемого:
![]() [f1(х)
+f2(х) + …dх]
=
[f1(х)
+f2(х) + …dх]
=
![]() f1(х)dх +
f1(х)dх +
![]() f2(х)dх + ….
f2(х)dх + ….
3. Постоянный множитель кв подинтегральном выражении выносится за знак интеграла:
![]() кf(х)dх = к
кf(х)dх = к![]() f(х)dх.
f(х)dх.
4. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл изменит свой знак на противоположный, сохранив абсолютную величину неизменной:
![]() f(х)dх = -
f(х)dх = -![]() f(х)dх.
f(х)dх.
5. Если отрезок [а,в] разбить на две части [а,с] и [с,в] , то интеграл:
![]() f(х)dх =
f(х)dх =![]() f(х)dх +
f(х)dх +![]() f(х)dх.
f(х)dх.
6.
![]() dх=в –а, приа ≠в . Это
свойство вытекает из того, что
неопределенный интеграл ∫ dх
= х, т.е. равен некоторой длине
отрезка, началом и концом которой будут
точкиаивэтого отрезка.
dх=в –а, приа ≠в . Это
свойство вытекает из того, что
неопределенный интеграл ∫ dх
= х, т.е. равен некоторой длине
отрезка, началом и концом которой будут
точкиаивэтого отрезка.
7. Если подинтегральная
функция на отрезке [а,в]
сохраняет постоянный знак, то и
определенный интеграл будет представлен
числом того же знака, т.е.:f(х)>0 и
![]() f(х)dх>0.
f(х)dх>0.
Существуют и другие свойства определенного интеграла, которые мы рассматривать не будем.
