Адекватность модели эксперименту

Функция отклика, аппроксимируемая полиномом, коэффициенты которой найдены по методу наименьших квадратов, может и не соответствовать (быть неадекватной) наблюдаемым значениям величины у.

Поэтому всегда, прежде чем использовать модель для исследования технической системы необходимо проверить ее адекватность (при нахождении мы опередили порядок исследования модели).

Для оценки используется критерий Фишера.

Наиболее надежные результаты проверки адекватности получают в планах, обеспечивающих одинаковую точность предсказания значений функции отклика в точках, находящихся на одинаковом расстоянии от центра эксперимента. Отметим, что ПФЭ удовлетворяет этому условию.

Проверку адекватности математической модели выполняем в несколько этапов:

1. Находим дисперсию адекватности:

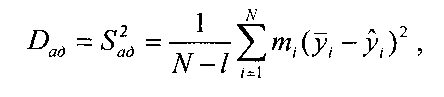
- число параллельных

опытов в і-ой строке матрицы планирования,-число коэффициентов аппроксимирующего многочлена.

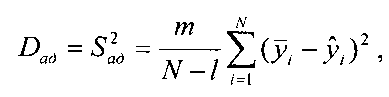Так как у нас, тоздесь

Jf_i-среднее наблюдаемое, у₍ - значение функции отклика, предсказанное по аппроксимирующему многочлену в i - ом опыте;

2. Находим F- критерия Фишера: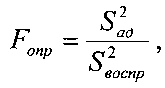где

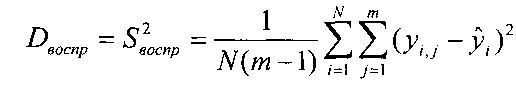, N- число опытов,

m -число повторяемости эксперимента в каждой вершине ПФЭ;

3. Определяем число степеней свободы:

1. Выбираем уровень значимости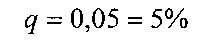- вероятность

ошибки первого рода (вероятность того, что правильная гипотеза будет отвергнута);

2. Используя таблицу критических значений критерия Фишера по

заданнымнаходим

Еслито считаем, что полученный аппроксимирующий

многочлен адекватен экспериментальным данным. B противном случае - нет.

Для проверки адекватности нашего аппроксимирующего многочлена произведем расчеты по предлагаемой программе на VBA :

Private Sub Workbook_Open()

Const n = 8, m = 3, L = 7, f1 = 1, f2 = 16

Const a = 17.875, b1 = 2.293, b2 = 1.762, b3 = -1.091, c1 = 1.656, c2 = -2.183, c3 = -1.212

Dim x1(1 To n), x2(1 To n), x3(1 To n) As Single

Dim y1(1 To n), y2(1 To n), y3(1 To n) As Single

Dim Ysr(1 To n), Yshap(1 To n) As Single

Dim Dad, Dvospr, Fop As Single

Dim i As Integer

x1(1) = 1: x1(2) = -1: x1(3) = 1: x1(4) = -1: x1(5) = 1: x1(6) = -1: x1(7) = 1: x1(8) = -1

x2(1) = 1: x2(2) = 1: x2(3) = -1: x2(4) = -1: x2(5) = 1: x2(6) = 1: x2(7) = -1: x1(8) = -1

x3(1) = 1: x3(2) = 1: x3(3) = 1: x3(4) = 1: x3(5) = -1: x3(6) = -1: x3(7) = -1: x3(8) = -1

y1(1) = 18.87: y1(2) = 13.92: y1(3) = 15.41: y1(4) = 16.88: y1(5) = 27.46: y1(6) = 17.68:

y1(7) = 14.76: y1(8) = 14.08

y2(1) = 18.47: y2(2) = 14.47: y2(3) = 17.67: y2(4) = 19.2: y2(5) = 28.89: y2(6) = 18.18:

y2(7) = 17.55: y2(8) = 12.39

y3(1) = 19.58: y3(2) = 12.87: y3(3) = 17.18: y3(4) = 16.89: y3(5) = 28.25: y3(6) = 17.01:

y3(7) = 17.93: y3(8) = 13.42

For i = 1 To n

Ysr(i) = (y1(i) + y2(i) + y3(i)) / 3

Yshap(i) = a + b1 * x1(i) + b2 * x2(i) + b3 * x3(i) + c1 * x1(i) * x2(i) + _

c2 * x1(i) * x3(i) + c3 * x2(i) * x3(i)

Next i

Dad = 0

For i = 1 To n

Dad = Dad + (Ysr(i) - Yshap(i)) ^ 2

Next i

Dad = Dad * m / (n - L)

Dvospr = 0

For i = 1 To n

Dvospr = Dvospr + (y1(i) - Yshap(i)) ^ 2 + (y2(i) - Yshap(i)) ^ 2 + (y3(i) - Yshap(i)) ^ 2

Next i

Dvospr = Dvospr / n / (m - 1)

Fop = Dad / Dvospr

Range("A1").Value = "Fop="

Range("B1").Value = Fop

Range("A2").Value = "Dvospr="

Range("B2").Value = Dvospr

Range("A3").Value = "Svospr="

Range("B3").Value = Dvospr ^ 0.5

End Sub

Значения вычисляемых параметров даны в следующей Excel - таблице

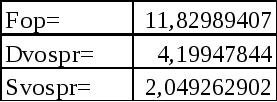
(Таблица 7)

Число степеней свободы: f_l = N -l =8-7 = 1, f₂ = N(m-1) =8 (3-1)= 16,

q = 0,05 =5%.

Значения критерия Фишера F для q = 0,05 Таблица 8

находим критическое значение параметра Фишера F = 4,5 . по таблице 8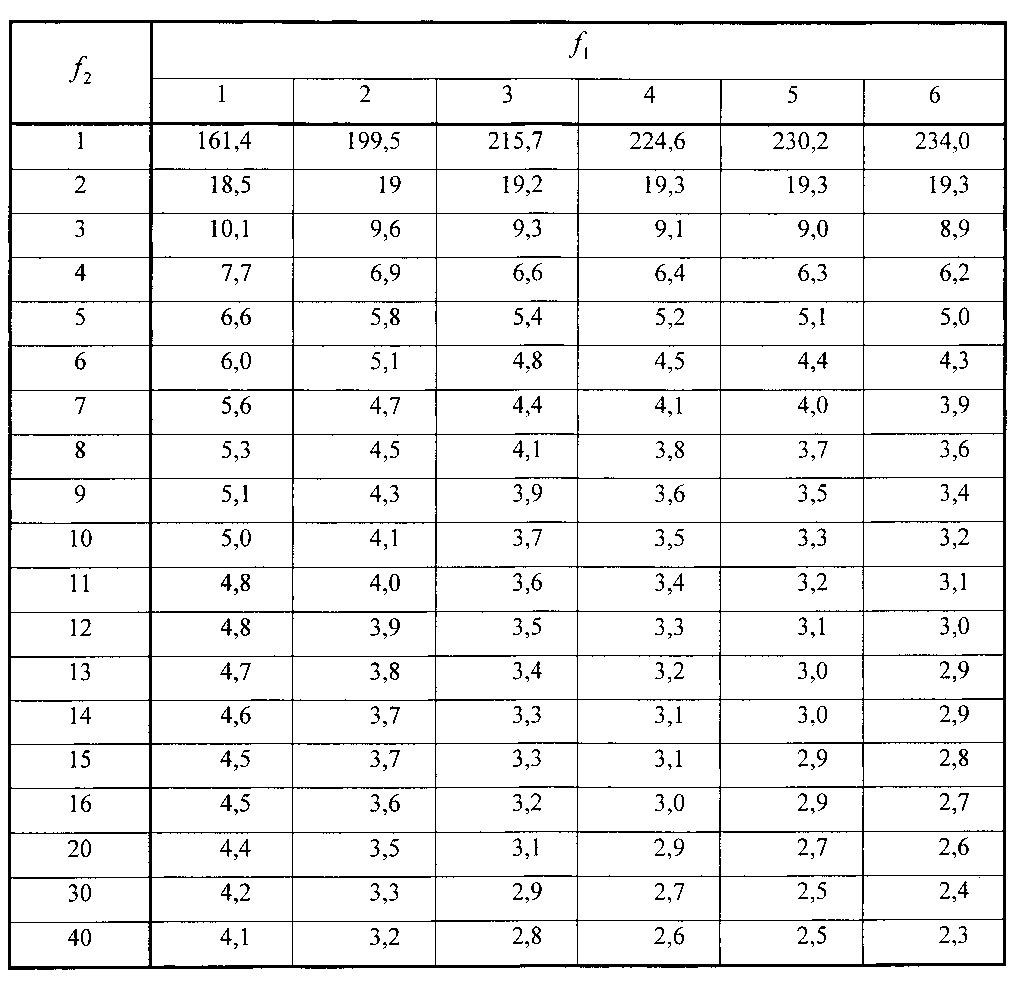

Таким образом, критерий Фишера F_кр=4,5. Т.к. F_ор=11.83 > F_кр. .

Полученный аппроксимирующий многочлен неадекватен экспериментальным данным.