
Курсовая работа
.pdfФедеральное агентство связи
ГОУ ВПО «Поволжский государственный университет телекоммуникаций и информатики»
Кафедра основ конструирования и технологии радиотехнических систем
ИССЛЕДОВАНИЕ РАСПРОСТРАНЕНИЯ СОБСТВЕННЫХ ВОЛН ЧАСТИЧНОЗАПОЛНЕННЫХ ПРЯМОУГОЛЬНЫХ ВОЛНОВОДОВ
Методические указания для выполнения курсовой работы по дисциплине «Электродинамика и распространение радиоволн»
(для студентов специальности 210302 — Радиотехника)
Составил: профессор Осипов О.В. Рецензент: профессор Неганов В.А.,
Самара 2010

2 |
Электродинамика и распространение радиоволн |
Цели и задачи дисциплины «Электродинамика и распространение радиоволн»
Основные задачи дисциплины «Электродинамика и распространение радиоволн» состоят в следующем:
—изучении законов электродинамики и исследование на их основе процессов излучения, при¸ ма и распространения волн
вразличных средах и направляющих системах, а также вопросов распространения радиоволн вблизи поверхности Земли, в е¸ атмосфере и в космическом пространстве;
—изучении основных закономерностей электромагнитного поля, а также рассмотрение технических устройств и систем, в которых используются различные способы управления электромагнитным полем;
—изучении электродинамических методов анализа волноведущих и резонансных систем СВЧ и КВЧ диапазонов, а также математических моделей, служащих для описания тех или иных электродинамических систем.
Врезультате изучения дисциплины «Электродинамика и распространение радиоволн» специалист должен:
—знать основные уравнения электродинамики и методы анализа полей в линиях передачи, объ¸ мных резонаторах и других элементах фидерного тракта;
—иметь представление об основных положениях электродинамики и особенностях их применения к исследованию электромагнитных явлений, играющих важнейшую роль в радиотехнике;
—знать механизмы распространения радиоволн различных диапазонов в свободном пространстве, с уч¸ том влияния поверхности Земли, тропосферы и ионосферы;
—иметь понятия о методах расч¸ та параметров электромагнитных волн в различных средах, а также представлять проблемы электромагнитной совместимости радиоэлектронных средств и пути их решения;
—получить практические навыки проведения простейших измерений характеристик электромагнитных волн в свободном пространстве, в линиях передачи и элементах фидерного тракта.

Методические указания к курсовому проектированию |
3 |
Специалист должен уметь:
–рассчитывать поля излучения простейших антенн;
–производить электродинамический анализ простейших волноведущих и резонансных систем.
Врамках курсового проектирования студент должен овладеть методами электродинамического анализа регулярных линий передачи СВЧ. Предлагается произвести расч¸ т дисперсионных характеристик и распределений электромагнитного поля собственных волн экранированного двухслойного прямоугольного волновода.
I.Теоретические основы
1.Общие сведения о регулярных линиях передачи
Устройство, ограничивающее область распространения электромагнитных колебаний и направляющее поток электромагнитной энергии в заданном направлении, называется линией передачи. Линии передачи служат для передачи (транспортировки) электромагнитной энергии от источника к потребителю, например, от передатчика к антенне и от антенны к при¸ мному устройству, а также для соединения отдельных частей и узлов радиоаппаратуры. Простейшим элементом, служащим для направления электромагнитной энергии, является плоская граница раздела двух сред, обеспечивающая полное внутреннее отражение падающей волны.
Линия передачи называется регулярной, если в продольном направлении неизменны е¸ поперечное сечение, положение в пространстве (например, нет поворота поперечного сечения вокруг какой-либо точки и т.п.) и электромагнитные свойства заполняющих е¸ сред. Линия передачи называется однородной, если в произвольном поперечном сечении параметры среды неизменны. Различают открытые линии и волноводы. В открытых линиях передачи отсутствует проводящий экран, ограничивающий область распространения электромагнитной энергии в поперечном сечении. В волноводах (экранированных линиях передачи) обязательно имеется одна или несколько поверхностей, ограничивающих область распространения электромагнитной волны в поперечном направлении. Особое место среди экранированных линий передачи занимают полые волноводы — металлические трубы того или иного поперечного сечения.
4 |
Электродинамика и распространение радиоволн |
а) |
б) |
в) |
г) |
|
|
|
|
|
|
|
|
д) |
|
|
е) |
|
ж) |
з) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и) |
к) |
л) |
м) |
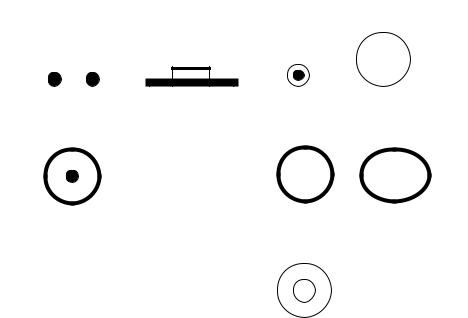
Рис. 1. Виды регулярных линий передачи
В технике связи применяются (рис. 1): двухпроводная (а), открытая полосковая (б), однопроводная (в), открытая диэлектрическая (г) линии передачи; коаксиальный кабель (д); прямоугольный (е), круглый (ж), эллиптический (з), прямоугольный двухслойный (и) волноводы; экранированная полосковая линия передачи (к), волоконный световод (л), плоский оптический волновод (м) и др.
Одной из основных характеристик линии передачи является понятие собственной волны. При этом под собственной волной линии передачи будем понимать электромагнитную волну, которая может распространяться в линии при создании необходимых условий. Таким образом, под собственными волнами волноведущей структуры будем понимать направляемые ею волны.
Линия передачи СВЧ или КВЧ-диапазонов на любой фиксированной частоте в общем случае может иметь бесконечное число собственных волн: распространяющихся и затухающих. Каж-

Методические указания к курсовому проектированию |
5 |
дая из этих собственных волн описывается своими собственными характеристиками. Распространяющиеся собственные волны линии передачи имеют характер бегущих волн. Затухающие собственные волны для данной фиксированной частоты являются нераспространющимися. Они возникают вблизи любой неоднородности в линии передачи при падении на не¸ какой-либо распространяющейся собственной волны. Такие волны быстро затухают при удалении от неоднородности и в процессе переноса энергии по линии передачи не участвуют.
Классификация направляемых волн. При выборе линии передачи решающее значение имеет тип волны, определяемый структурой электромагнитного поля и критической частотой
— частотой, на которой прекращается перенос энергии. Эти характеристики определяются из решения соответствующей граничной задачи о собственных волнах линии передачи. Как правило, линии передачи используются в режиме основной волны, имеющей наименьшую критическую частоту fкр . Однако в некоторых случаях предпочтение отда¸ тся волнам высших типов с критическими частотами, превышающими критическую частоту основной волны.
Различают следующие типы (классы) волн:
а) Т-волны (поперечные электромагнитные волны; от англ. «transverse» — поперечный), не содержащие продольных (по отношению к направлению переноса энергии) составляющих электромагнитного поля. Они существуют только в линиях передачи, имеющих не менее двух изолированных проводников, прич¸ м для них критическая частота fкр = 0 ;
б) Е (ТМ)-волны (электрические волны), не имеющие продольной составляющей магнитного поля. У них имеется продольное электрическое поле. Эти волны называют поперечномагнитными;
в) Н (ТЕ)-волны (магнитные волны), не имеющие продольной составляющей электрического поля. Эти волны называют
поперечно-электрическими;
г) LE-волны (продольно-электрические волны), у которых в поперечном сечении линии передачи (при соответствующем выборе системы координат) присутствует только одна составляющая электрического поля;

6 |
Электродинамика и распространение радиоволн |
д) LM-волны (продольно-магнитные волны), у которых в поперечном сечении линии передачи (при соответствующем выборе системы координат) присутствует только одна составляющая магнитного поля;
е) гибридные волны типа НЕ или ЕН, для которых характерно наличие всех шести составляющих электромагнитного поля.
Н- и Е-волны существуют в волноводах с однородным диэлектрическим заполнением. Критические частоты этих волн отличны от нуля и зависят от формы и размеров поперечного сечения, а также от параметров заполняющего диэлектрика.
LE- и LM-волны характерны для частично заполненных про- дольно-однородных прямоугольных волноводов.
2. Общий метод исследования собственных волн регулярных линий передачи
Задача исследования поля в линии передачи состоит в определении структуры поля, установлении условий распространения различных типов направляемых волн и нахождении их параметров.
Пусть имеется регулярная линия передачи с произвольным поперечным сечением и декартовая система координат {XYZ}, прич¸ м ось OZ совпадает с направлением распространения волны. Ввиду поперечной неоднородности структуры поле не может быть неизменным в плоскости z = const и поэтому в уравнениях Максвелла уже нельзя заранее положить ∂ / ∂x = 0 или ∂ / ∂y = 0 . Понятно также, что постоянная распространения волны в линии передачи (обозначим е¸ через γ ) в общем случае будет отличаться от волнового числа k = ω
 εaμa . Для комплексных амплитуд векторов напряж¸ нности электрического и магнитного полей волны, распространяющейся вдоль оси OZ, можно записать следующие выражения:
εaμa . Для комплексных амплитуд векторов напряж¸ нности электрического и магнитного полей волны, распространяющейся вдоль оси OZ, можно записать следующие выражения:
E(x, y, z) = er(x, y)e−i γz , |
(2.1) |
|
r |
r |
|
H(x, y, z) = h(x, y)e−i γz |
, |
|
где функции er(x,y), h (x,y) описывают распределение электромагнитного поля в поперечном сечении линии. Параметр γ называется продольным волновым числом или постоянной распространения волны.

Методические указания к курсовому проектированию |
7 |
Векторы E и H поля волны, распространяющейся в линии передачи, подчиняются однородным уравнениям Гельмгольца:
Ñ2E + k2E = 0, Ñ2H + k2H = 0 . |
(2.2) |
Применяя оператор Лапласа, например, к вектору E , получаем:
r |
æ |
¶2 |
|
Ñ2E = ç |
|
+ |
|
|
|||
|
ç |
¶ x2 |
|
|
è |
|
|
¶2 |
|
¶2 |
ö r |
2 |
r |
2 |
r |
|
||
|
|
|
|
|
÷ |
|
|
|
||
|
2 + |
|
2 |
|
|
|
E , |
(2.3) |
||
¶ y |
¶ z |
÷ E = Ñ E - g |
|
|||||||
|
|
|
ø |
|
|
|
|
|
||
где
Ñ2 = |
¶2 |
+ |
¶2 |
. |
|
¶ x2 |
¶ y2 |
||||
|
|
|
Учитывая (2.3), уравнения Гельмгольца (2.2) переходят в следующие двумерные уравнения относительно векторных функций e и h :
Ñ2 er |
(x, y) + g2 er |
(x, y) = 0, |
r |
r |
(2.4) |
Ñ2 h (x, y) + g2 h (x, y) = 0,
где g2 = k2 - g2 — поперечное волновое число; k = k0 
 em .
em .
Векторные уравнения (2.4) можно представить в виде системы шести скалярных уравнений. Обычно решают уравнения относительно продольных составляющих векторов поля:
Ñ2 ez + g2 ez = 0, (2.5)
Ñ2 hz + g2 hz = 0,
а поперечные составляющие определяют через продольные с помощью соотношений связи, вытекающих из уравнений Максвелла. В декартовой системе координат они имеют вид:
ex = - |
iγ |
∂ez |
- |
iωμa |
∂hz |
, |
|||||
g2 |
|
|
|||||||||
|
|
¶ x |
|
|
g2 |
|
¶ y |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
hx = |
iwea |
¶ez |
- |
ig |
¶hz , |
|
|||||
|
|
|
|||||||||
|
g2 |
|
¶ y |
|
|
g2 |
¶ x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ey
hy
= - |
|
iγ |
∂ez + |
iωμa |
∂hz |
, |
||||||
|
|
g2 |
||||||||||
|
g2 |
|
|
¶ y |
¶ x |
|
||||||
|
|
|
|
|
|
|
|
|
|
(2.6) |
||
|
|
iwea |
|
|
ig |
|
|
|||||
= - |
¶ez |
- |
¶hz . |
|||||||||
|
|
|||||||||||
|
|
g |
2 |
|
¶ x |
|
g2 |
¶ y |
|
|||
|
|
|
|
|
|
|
|
|
||||
Уравнения (2.5) решаются методом разделения переменных, согласно которому искомое решение представляется в виде произведения функций, зависящих только от одной координаты. Например, решение первого уравнения из (2.5) в декартовой

8 |
Электродинамика и распространение радиоволн |
системе координат ищется в виде:
ez (x, y) = e1(x) e2(y) . |
(2.9) |
Выражение (2.9) описывает общее решение первого уравнения системы (2.5). Из него необходимо выделить только те частные решения, которые удовлетворяют граничным условиям на проводящих стенках (экране) и границах раздела сло¸ в конкретной линии передачи.
3.Метод разделения переменных в декартовой системе координат
Вдекартовых координатах двумерное уравнение Гельмгольца имеет вид
∂2Ψ |
∂2Ψ |
|
Ψ = 0, |
(3.1) |
i + |
i + γ2 |
|||
∂x2 |
∂y2 |
|
i |
|
|
|
|
||
где через Ψi обозначена одна из продольных составляющих ez или hz . Применение метода разделения переменных подразумевает, что неизвестное решение Ψi можно представить в виде произведения функций разных координат
Ψi (x, y) = X(x)Y(y) . |
(3.2) |
Подстановка представления (3.2) в уравнение (3.1) приводит к соотношению:
− |
1 ∂2X |
= |
1 ∂2Y |
+ γ2 . |
(3.3) |
|||
|
|
|
|
|||||
X ∂ x2 |
Y ∂ y2 |
|||||||
|
|
|
|
|||||
Так как слева и справа стоят функции независимых аргументов, то они должны быть независимы, а, следовательно, левая и правая часть равны одной постоянной, которую мы обозначим через постоянную rx2 . Тогда вместо (3.3) получаем два дифференциальных уравнения:
|
d2X |
+ r2X = 0, |
|
d2Y |
+ r2Y = 0, |
(3.4) |
||
|
|
|
||||||
|
dx2 |
x |
|
|
dy2 |
y |
|
|
|
|
|
|
|
|
|||
в которых |
|
|
|
|
|
|
|
|
|
|
r2 |
= γ2 |
− r2 . |
|
(3.5) |
||
|
|
y |
|
|
x |
|
|
|

Методические указания к курсовому проектированию |
9 |
Общие решения уравнений (3.4) можно выразить, например, в тригонометрической форме:
X(x) = A cos (rxx) + B sin (rxx), |
(3.6) |
|
Y(y) = C cos (ryy) + D sin (ryy), |
||
|
||
где A, B, C, D — неизвестные постоянные. |
|
В результате для функции Ψi (x, y) получаем следующее выражение:
Yi (x, y) = [A cos (rxx) + B sin (rxx)][Ccos (ryy) + D sin (ryy)]. (3.7) Поставим первую краевую задачу (задачу Дирихле) для волновода с поперечным сечением в виде прямоугольника: 0 ≤ x ≤ a; 0 ≤ y ≤ b . Будем считать, что функция Ψi = 0 на контуре поперечного сечения (то есть при x = 0, a; y = 0, b ). Подстановка (3.7) в указанное граничное условие приводит к решению
|
Yi = Y0i sin (rxx) sin (ryy), |
|
|
|
(3.8) |
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
r = |
mp |
; m = |
|
, |
r = |
np |
; n = |
|
, |
|
|
1, ¥ |
1, ¥ |
(3.9) |
|||||||||
|
|
||||||||||
x |
a |
|
|
|
y |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ψ0i — новая неизвестная постоянная.
Таким образом, мы получили систему решений краевой задачи Дирихле для двумерного уравнения Гельмгольца в случае прямоугольной области. Это собственные функции Ψimn(1) , с собственными значениями g2 mn :
|
(1) |
(1) |
|
æ mpx ö |
æ npyö |
|
||||||||||||
Yimn |
= Nmn sinç |
|
|
|
|
÷ |
sinç |
|
|
÷ , |
|
|
|
|
||||
|
|
a |
|
|
|
|
||||||||||||
|
|
|
|
|
è |
|
|
ø |
è |
b ø |
(3.10) |
|||||||
|
|
æ mpö2 |
æ npö2 |
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
g |
mn |
= ç |
|
÷ |
+ |
ç |
|
÷ , ( m = 1, ¥, n = 1, ¥ ), |
|
|||||||||
|
è a |
ø |
|
è b |
ø |
|
|
|
|
|
|
|
|
|||||
где Nmn(1) — неопределенные постоянные. |
|
|
В случае второй краевой задачи (задачи Неймана) на реше- |
||
ние (3.7) следует наложить другие граничные условия: |
|
|
¶ Yi = 0 при x = 0, a ; |
¶ Yi = 0 при y = 0, b . |
(3.11) |
¶x |
¶ y |
|
В результате получим систему решений краевой задачи Неймана для прямоугольной области в следующем виде:
10 |
Электродинамика и распространение радиоволн |
|||
|
Y |
|
|
|
|
b1 |
|
|
σэкр = ∞ |
|
1 |
ε1, μ1 |
a |
X |
|
0 |
|||
|
ε2, μ2 |
|
|
|
|
2 |
|
|
|
|
− b2 |
|
|
|
|
Z |
|
|
|
|
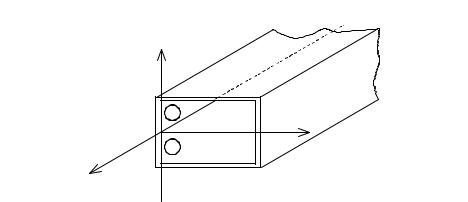
Рис. 2. Прямоугольный двухслойный волновод |
|||
|
(2) |
|
(2) |
|
æ mpx ö |
æ npyö |
|
||||||||||
Yimn |
= Nmn cosç |
|
|
|
÷ |
cosç |
|
|
÷ , |
|
|
|
|
||||
|
a |
|
|
|
|
||||||||||||
|
|
|
|
|
è |
|
ø |
è |
b ø |
(3.10) |
|||||||
|
|
æ mpö2 |
æ npö2 |
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
g |
mn |
= ç |
|
÷ |
+ ç |
b |
÷ , |
( m = (0), ¥, n = (0), ¥ ), |
|
||||||||
|
è |
a ø |
è |
ø |
|
|
|
|
|
|
|
|
|
||||
где Nmn(2) — неопределенные постоянные. Символ (0) обозначает, что индексы m и n одновременно не могут обращаться в нуль.
4. Электродинамический анализ прямоугольного двухслойного волновода
На рис. 2 представлена геометрия экранированного прямоугольного волновода с двумя диэлектрическими плоскопараллельными слоями. Параметры диэлектрических сло¸ в равны соответственно ε1, μ1 и ε2, μ2 . Обозначим через a ширину волновода, а через b1 и b2 — толщины первого и второго слоя соответственно. Будем считать экран волновода идеально-проводящим и не учитывать потери в диэлектриках.
При решении задач о собственных волнах многослойных волноведущих структур обычно используется метод частичных областей. Его суть заключается в следующем. На первом этапе решения задачи из системы уравнений Максвелла с уч¸ том граничных условий на идеально-проводящих стенках определяются поля отдельно в каждом из диэлектрических сло¸ в. Полученные решения будут содержать неизвестные постоянные, которые на втором этапе решения определяются из постановки граничных условий на
