
Курсовая работа
.pdf
Методические указания к курсовому проектированию |
11 |
границах раздела сло¸ в. Второй этап решения задачи обычно называется сшиванием полей. Отметим, что на границе раздела диэлектрических сло¸ в непрерывными функциями являются касательные составляющие векторов E и H .
Применим описанный выше алгоритм для нахождения дисперсионных характеристик двухслойного прямоугольного волновода.
В силу регулярности линии передачи вдоль оси OZ будем искать решения для комплексных амплитуд в каждой из отдельных областей в виде (l = 1, 2 ):
E(l)(x, y, z) = e(l)(x, y)e−i γz , H(l)(x, y, z) = h(l)(x, y)e−i γz , (4.1)
где γ — неизвестная пока постоянная распространения вдоль оси OZ; верхний индекс «l» показывает на принадлежность к соответствующей области.
Постановка краевой задачи для ez для первой области имеет
следующий вид: |
|
|
|
|
|
|
Ñ2 e(1) |
+ g2 |
e(1) |
= 0 |
при 0 < x < a , 0 < y < b ; |
|
|
z |
1 |
z |
|
|
1 |
(4.2) |
|
e(1) |
= 0 |
при x = |
0, x = a, y = b , |
||
|
|
|||||
|
|
z |
|
|
1 |
|
где γ2 1 = ω2εa1μa1 − γ2 ; |
индекс «(1)» указывает на принадлежность |
|||||
к первому слою. |
|
|
|
|
|
|
При анализе частично-заполненных волноводов, в отличие от однороднозаполненных, не уда¸ тся провести анализ отдельно для E- и H-волн. Поэтому краевая задача (4.8.2) должна быть дополнена аналогичной задачей для hz :
Ñ2 hz(1) + g2 1hz(1)
¶h(1)
z = 0 при
¶ x
= 0 |
при 0 < x < a , 0 < y < b1 ; |
||
|
|
¶h(1) |
(4.3) |
x = 0, |
x = a; |
z = 0 |
при y = b . |
|
|
¶ y |
1 |
|
|
|
|
X-составляющие электромагнитного поля определяются из формул:
hx(l) = |
|
i |
¶e(l) |
|
|
||
|
|
|
|
z |
(LE - волны); |
|
|
k0ml |
|
||||||
|
|
¶ y |
|
(4.4) |
|||
|
|
i |
|
¶h(l) |
|||
ex(l) = - |
|
|
|||||
|
|
|
z |
(LM - волны). |
|
||
k0el |
|
¶ y |
|
||||
|
|
|
|
|
|||

12 |
Электродинамика и распространение радиоволн |
В системе уравнений (4.4) верхние индексы «(l)» указывают на то, что данные соотношения справедливы для областей 1 и 2..
Несложно записать решения краевых задач (4.2) и (4.3) в виде:
ez(1)(x, y) = A1 sin(kx1x){cos(ky1y) - ctg(ky1b1) sin(ky1y)} |
, |
hz(1)(x, y) = B1 cos(kx1x){cos(ky1y) + tg(ky1b1)sin(ky1y)} , |
(4.5) |
|
где kx1 = πm / a , ky1 = 
 γ2 1 − kx21 , m = 0, 1, 2, 3, . . . ; A и B — неопредел¸ нные постоянные.
γ2 1 − kx21 , m = 0, 1, 2, 3, . . . ; A и B — неопредел¸ нные постоянные.
Постановки краевых задач для составляющих ez , hz для вто-
рой области записываются аналогичным образом: |
|
|||||||||||||||
|
Ñ2 e(2) |
|
+ g2 |
|
e(2) |
= 0 |
|
при 0 < x < a , - b |
< y < 0; |
|
||||||
|
|
z |
|
|
2 |
|
z |
|
|
|
2 |
|
|
(4.6) |
||
|
|
|
|
|
|
e(2) |
= 0 |
при x = 0, x = a, y = - b , |
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
2 |
|
|
Ñ2 h(2) |
+ g2 |
|
|
h(2) = 0 |
|
при 0 < x < a , - b |
|
< y < 0; |
|
||||||
|
|
z |
|
|
2 |
z |
|
|
|
2 |
|
(4.7) |
||||
|
¶h(2) |
= 0 |
при x = |
0, x = a, |
|
¶h(2) |
|
|
||||||||
|
z |
|
|
z = 0 |
при y = - b , |
|||||||||||
|
¶ x |
|
|
|
|
|
|
|
|
|
|
¶ y |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
g2 2 = w2ea2ma2 |
- g2 ; верхний индекс «(2)» подч¸ ркивает при- |
||||||||||||||
надлежность ко второму слою. |
|
|
|
|
|
|||||||||||
Решения краевых задач (4.6) и (4.7) имеют вид: |
|
|||||||||||||||
|
ez(2)(x, y) = A2 |
sin(kx2x){cos(ky2y) + ctg(ky2b2)sin(ky2y)} |
, |
|||||||||||||
|
hz(2)(x, y) = B2 cos(kx2x){cos(ky2y) - tg(ky2b2)sin(ky2y)} , |
(4.8) |
||||||||||||||
|
|
|||||||||||||||
где |
kx2 = kx1 = πm / a , |
ky2 = |
|
γ2 2 − kx2 |
2 , m = 0, 1, 2, 3, . . . ; С и D |
|||||||||||
— неопредел¸ нные постоянные. |
|
|
|
|
|
|||||||||||
Выражения (4.5) и (4.8) для продольных составляющих полей содержат четыре неизвестные постоянные A1,2; B1,2 . Для их определения воспользуемся граничными условиями на границе раздела сло¸ в при y = 0 :
ez(1) |
= ez(2) |
, |
hz(1) |
= hz(2) |
, |
hx(1) = hx(2) (LE - волны); |
(4.9) |
|||
ez(1) |
= ez(2) |
, |
hz(1) |
= hz(2) |
, |
ex(1) |
= ex(2) |
(LM - волны). |
||
|
||||||||||
Явные выражения для x-составляющих полей получаются из (4.4) с уч¸ том (4.5) и (4.8). Для LE-волн достаточно использовать три верхних условия (4.9); для LM-волн — три нижних.

Методические указания к курсовому проектированию |
13 |
Из граничных условий (4.9) для LE-волн следует:
A = A , B = B , |
|
- |
ky1 |
ctg(k |
|
b ) = |
ky2 |
|
ctg(k |
y2 |
b ); |
|||||||
|
|
|
|
|
|
|||||||||||||
1 |
2 |
1 |
2 |
|
|
m1 |
|
y1 1 |
m2 |
|
|
2 |
||||||
для LM-волн: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A |
= A , |
B |
= B , - |
ky1 |
tg(k |
b ) = |
ky2 |
tg(k |
b ); |
|||||||||
|
|
|||||||||||||||||
1 |
2 |
1 |
|
2 |
|
|
e1 |
|
|
y1 1 |
|
e2 |
|
|
y2 |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из (4.10а,б) следуют два дисперсионных уравнения:
ky1 m2 ctg(ky1b1) + ctg(ky2b2) = 0,
ky2 m1
ky1 e2 tg(ky1b1) + tg(ky2b2) = 0,
ky2 e1
(4.10а)
(4.10б)
(4.11)
(4.12)
Дисперсионное уравнение (4.11) описывает распространение LEволн, а уравнение (4.12) — LM-волн. Поля, соответствующие этим собственным волнам, характеризуются отсутствием одной из поперечных компонент электрического или магнитного полей соответственно.
В частности, у LE (продольно-электрической) волны отсутствует поперечная составляющая электрического поля, перпендикулярная к границе раздела диэлектрических сло¸ в ( Ey º 0, Hy ¹ 0). У LM (продольно-магнитной) волны отсутствует поперечная составляющая магнитного поля, перпендикулярная к границе раздела
диэлектрических сло¸ в ( Hy º 0, Ey ¹ 0).
Рассмотрим классификацию собственных волн двухслойного прямоугольного волновода. Будем характеризовать LE и LM-волны двумя целочисленными индексами m и n (m = (0), 1, 2, . . . ; n = (0), 1, 2, . . . ). С индексом m будем связывать число вариаций поля вдоль широкой стенки волновода, а с индексом n — порядковый номер корня одного из уравнений (4.11) или (4.12). Поэтому будем обозна-
чать собственные волны как LEmn и |
LMmn - волны. |
||||||
Каждое из уравнений (4.11), (4.12) |
совместно с условиями |
||||||
2 |
æ mpö 2 |
|
2 |
|
2 |
||
k1,2 |
= ç |
|
÷ |
+ ky1,2 |
+ g |
|
|
|
|
||||||
|
è |
a ø |
|
|
|
|
|
образуют две системы из тр¸ х уравнений каждая относительно неизвестных: ky1,2 , g . Решение этих систем да¸ т дисперсионные зависимости γ = γ(ω) .

14 |
Электродинамика и распространение радиоволн |
5. Методика расч¸ та дисперсионных характеристик
Рассмотрим методику расч¸ та дисперсионных характеристик двухслойного прямоугольного волновода на примере дисперсионного уравнения для LE-волн (4.11), которое имеет вид:
ky2 |
μ |
b ) + tg (k |
|
) = 0 , |
|
|
1 tg (k |
b |
(5.1) |
||
|
|||||
ky1 |
μ2 |
y1 1 |
y2 2 |
|
|
|
|
|
|
где ky1,2 = 
 k02ε1,2μ1,2 − γ2 − (πm / a)2 ; k0 — волновое число для вакуума; εj,μj (j = 1, 2) — относительные диэлектрические и магнит-
k02ε1,2μ1,2 − γ2 − (πm / a)2 ; k0 — волновое число для вакуума; εj,μj (j = 1, 2) — относительные диэлектрические и магнит-
ные проницаемости первого и второго сло¸ в. Целое число m указывает на первый индекс собственной волны и при расч¸ те дисперсионной характеристики зада¸ тся.
Дисперсионная характеристика представляет собой график зависимости γ = γ(k0 ) . Однако, как видно из уравнения (5.1 ) данную зависимость в явном виде получить не представляется возможным. Поэтому дисперсионное уравнение для собственных волн регулярной линии передачи запишем следующим образом:
F(γ,k0 ) = 0 . |
(5.2) |
Уравнение (5.2) является трансцендентным и может быть решено только численными методами.
На первом этапе производится переход от величин γ и k0 , имеющих размерность 1/м к безразмерным параметрам. Будем использовать четыре нормированных параметра:
V = k0b1 — нормированная толщина первого слоя; B2 = k0b2 — нормированная толщина второго слоя;
W= k0a — нормированная ширина волновода;
Γ= (γ /k0)2 — квадрат нормированной постоянной распространения.
Используя новые нормированные параметры, несложно переписать уравнение (5.1) в следующем виде:
|
|
tg (V |
|
)+ |
|
|||||
μ |
ε μ − Γ − (πm/ W)2 |
ε μ − Γ − (πm/ W)2 |
||||||||
1 |
2 |
2 |
|
|
1 |
1 |
|
|
|
|
|
tg (B |
|
)= 0. |
|||||||
+ μ |
ε μ − Γ − (πm/ W)2 |
ε μ − Γ − (πm/ W)2 |
||||||||
2 |
|
1 |
1 |
|
2 |
2 |
2 |
|
|
|
Заметим, что в уравнении (5.3.) параметры B1, B2 и V няются в пределах 0 .. ~10.
(5.3)
изме-

Методические указания к курсовому проектированию |
15 |
В нормированных переменных дисперсионное уравнение имеет вид:
F(Γ, V) = 0 . |
(5.4) |
Алгоритм определения дисперсионной характеристики имеет следующий вид:
1. На первом этапе находятся частоты отсечек V собственных волн пут¸ м численного решения уравнения:
F(Γ = 0, V) = 0 , |
(5.5) |
которое получается из (5.3) при Γ = 0 . Уравнение (5.5) имеет дискретный набор корней V = Vn (n = 1,2, . . .). Каждый из корней Vn определяет нормированную частоту отсечки волны LEmn ( m = 0, 1, ... — зада¸ тся явным образом). Например, первый корень уравнения (5.5) определяет частоту отсечки волны LEm1 и т.д.
2. На втором этапе производится численный расч¸ т характеристики Γ = Γ(V) . Для этого в уравнении (5.4) нормированная частота полагается равной V = V1 + DV × i ( V — шаг по нормированной частоте, i — целое число) и на каждом шаге численно решается уравнение (5.3) при фиксированном значении V .
Очевидно, что при V1 < V < V2 уравнение (5.3) имеет один корень, соответствующий волне LEm1 , при V2 < V < V3 уравнение (5.3) имеет уже два корня, больший из которых соответствует постоянной распространения волны LEm1 , а меньший — LEm2 и т.д.
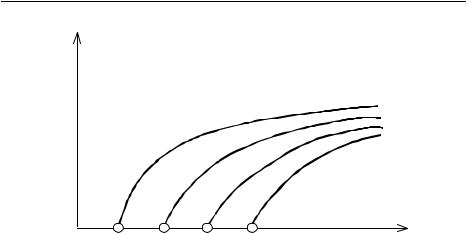
Таким образом, для каждой частоты V пут¸ м численно решения уравнения (5.4) определяется набор корней Γp (p = 1, 2, . . .) , каждый из которых соответствует собственной волне LEm,N−p+1 (N — общее чило корней на частоте V). В результате строится график функции Γ = Γ(V), которая имеет несколько ветвей, соответствующих различным собственным волнам.
Примерный вид дисперсионной характеристики представлен на рис.3. По оси абсцисс отложены значения нормированной частоты V, а по оси ординат — соответствующие им значения нормированной постоянной распространения Г. Кружками отмечены частоты отсечек собственных волн.
Затем необходимо решить дисперсионное уравнение (5.4) для других значений индекса m и определить характеристики волн LE1n .
Для построения дисперсионных характеристик LM-волн необходимо численно решать уравнение (4.12), предварительно перейдя в н¸ м к нормированным переменным.
16 |
Электродинамика и распространение радиоволн |
Γ
LEm1
LEm2
LEm3
LEm4
V1 |
V2 |
V |
V |
V |
|
|
3 |
4 |
|
Рис. 3. Типичный вид дисперсионных характеристик линий передачи
6. Расч¸ т распределений составляющих электромагнитного поля
После того, как построены дисперсионные характеристики для собственных волн осуществляется расч¸ т распределений составляющих векторов электромагнитного поля вдоль осей OX и OY.
Рассмотрим его на примере расч¸ та составляющей ez LE- волн прямоугольного двухслойного волновода. Составляющая ez в первом и втором слоях волновода определяется из выражений (4.5) и (4.8), соответственно. Распределение составляющей ez вдоль оси OX описывается следующей формулой:
e(1) |
(x) = e(2) |
(x) = e |
sin (πmx / a), |
(6.1) |
z |
z |
0z |
|
|
где e0z — начальная амплитуда при x=0.
Соотношение (6.1) записано с уч¸ том того, что распределение составляющей ez вдоль координаты X будет одинаковым для обоих сло¸ в волновода. Удобно в (6.1) провести нормировку:
ez (x) |
= sin (πmx / a) при x [ 0, a] . |
(6.2) |
||
e0z |
|
|||
|
|
|||
Подставляя в выражения (6.2) различные значения индекса m получаем распределения составляющей ez вдоль координаты x для волн LEmn .

Методические указания к курсовому проектированию |
17 |
Распределение поля составляющей ez вдоль оси OY будет различным в обоих слоях и определяться следующими формулами:
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|||
(1) |
|
|
2 |
- g |
2 |
|
- |
|
|
2 |
|
- |
|
|
|
|
|
|
|
|
|||||||||||
ez |
(y) = e0z {sin ç |
|
k0e1m1 |
|
|
|
|
(pm / a) |
|
|
y÷ |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
||
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
ö |
æ |
|
|
|
|
|
|
|
|
|
ö |
|
|||||
|
2 |
- g |
2 |
|
|
|
2 |
|
|
b1 |
2 |
|
|
|
2 |
- (pm / a) |
2 |
|
|
||||||||||||
- tg ç |
k0e1m1 |
|
|
- (pm / a) |
|
|
|
÷ cos ç |
k0e1m1 - g |
|
|
y÷} , |
|||||||||||||||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
(6.3) |
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|||
(2) |
|
|
2 |
- g |
2 |
- (pm / a) |
2 |
- |
|
|
|
|
|
|
|
|
|||||||||||||||
ez |
(y) = e0z {sin ç |
|
|
k0e2m2 |
|
|
|
|
|
y÷ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
||
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
æ |
|
|
|
|
|
|
|
|
|
|
ö |
|
|||
|
2 |
- g |
2 |
- (pm / a) |
2 |
|
|
b2 |
|
|
2 |
|
|
|
2 |
|
2 |
|
} , |
||||||||||||
- tg ç |
k0e2m2 |
|
|
|
|
|
÷ cos ç |
|
k0e2m2 - g |
|
- (pm / a) |
y÷ |
|||||||||||||||||||
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
где e0z — амплитуда при y=0.
Произвед¸ м в выражениях (6.3) нормировку, аналогично п.5. Тогда соотношения (6.3) принимают следующий вид:
ez(1)(y) |
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
= sin |
çy¢ |
e m |
1 |
- G - (pm / W) |
|
÷ |
- |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
e0z |
|
|
|
|
|
è |
|
|
1 |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
ö |
æ |
|
|
|
|
|
|
|
|
|
|
ö |
|
|
e m |
|
|
|
|
|
|
2 |
|
|
|
|
e m |
|
- G - (pm / W) |
2 |
||||||||||
- tg ç V |
1 |
- G - (pm / W) |
÷ cos çy¢ |
|
|
1 |
|
÷ , |
||||||||||||||||||
è |
|
1 |
|
|
|
|
|
|
|
ø |
è |
|
|
|
|
1 |
|
|
|
ø |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ez(2)(y) |
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
(6.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
= sin |
çy¢ |
e m |
2 |
- G - (pm / W) |
|
÷ |
- |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
e0z |
|
|
|
|
|
è |
|
|
2 |
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
æ |
|
|
|
|
|
|
|
|
|
|
ö |
|
|
e |
|
m |
|
- G - |
(pm / W) |
2 |
|
|
|
|
e m |
|
- G - (pm / W) |
2 |
||||||||||
- tg çB |
|
2 |
2 |
|
÷ cos |
çy¢ |
|
2 |
÷ , |
|||||||||||||||||
è |
2 |
|
|
|
|
|
|
|
|
|
|
ø |
è |
|
|
|
2 |
|
|
|
ø |
|||||
где y′ = k0y — безразмерная координата.
Из соотношений (6.4) видно, что распределения полей вдоль координаты y зависят от точки дисперсионной кривой (V,Γ) . Если нам необходимо рассчитать эпюру составляющей ez , например, для волны LE11 , то сначала рассчитывается дисперсионная характеристика для этой волны и определятся точка (V,Γ) , принадлежащая этой кривой (это делается автоматически при нахождении корней дисперсинного уравнения). После этого рассчитываются распределения составляющей ez по формулам (6.4) при изменении параметра y′ = k0y от − B2 до нуля (расч¸ т по второй формуле из (6.4)) и от нуля до V (рас- ч¸ т по первой формуле из (6.4)).
Расч¸ т распределения составляющей hz(1,2) производится по вторым формулам систем (4.5) и (4.8). X-составляющие электромагнитного поля вычисляются по формулам (4.4) с использованием выражений для продольных компонент (4.5) и (4.8).

18 |
Электродинамика и распространение радиоволн |
II. Задания для курсового проектирования
Целью курсовой работы является электродинамический анализ прямоугольного двухслойного волновода, стенки которого являются либо электрическими, либо «магнитными». На электрической стенке (в задании она обозначается сплошной линией) выполняются следующие граничные условия:
ez = 0, |
∂ hrz |
= 0. |
|
∂ n |
|
На «магнитной стенке» (в задании она обозначается штриховой линией) выполняются граничные условия:
hz = 0, |
∂ erz |
= 0. |
|
∂ n |
|
В последних соотношениях n = (x,y) |
— нормальная координата. |
|
Курсовая работа проводится в несколько этапов.
1.Теоретический вывод дисперсионных уравнения для LE и LM-волн прямоугольного двухслойного волновода из Вашего варианта задания.
2.Переход к нормированным параметрам в полученных в п.1 дисперсионных уравнениях.
3.Численный расч¸ т дисперсионных характеристик для соб-
ственных волн LEmn или LMmn при m = 0,1; n = 1,2,3,4 (всего 8 низших типов собственных волн).
4.Определение частотного диапазона одноволновости частич- но-заполненного прямоугольного волновода по значениям частот отсечек двух низших LE или LM-волн.
5.Расч¸ т распределений поля составляющей ez вдоль осей
OX и OY для |
собственных волн LEmn или LMmn при |
m = 0,1; n = 1,2,3,4 |
(всего 8 распределений ez вдоль оси OX и 8 |
распределений ez |
вдоль оси OY). |
В пояснительной записке к курсовой работе должны присутствовать:
1.Задание на курсовую работу (рисунок поперечного сечения рассчитываемой структуры, физические и геометрические параметры сло¸ в).
2.Подробный теоретический вывод дисперсионных уравнений для LE или LM-волн рассматриваемой структуры с комментариями.
Методические указания к курсовому проектированию |
19 |
3.Дисперсионные уравнения для LE или LM-волн рассматриваемой структуры в нормированном виде.
4.Графики дисперсионных характеристик Γ = Γ(V) для 8 низших типов собственных волн рассматриваемой структуры.
5.Определение основного типа волны и вычисление частотного диапазона одноволновости.
6.Графики распределений составляющей ez для 8 низших типов собственных волн (16 графиков). Вывод о том, какой физический смысл имеет второй индекс n в обозначении LE или LM-волн.
7.Список используемой литературы.
Параметры, используемые при расч¸ те волноведущей структуры:
ε1 = 15, μ1 = 1, k0a = 4, ε2 = 9, μ2 = 1, k0b2 = 2.
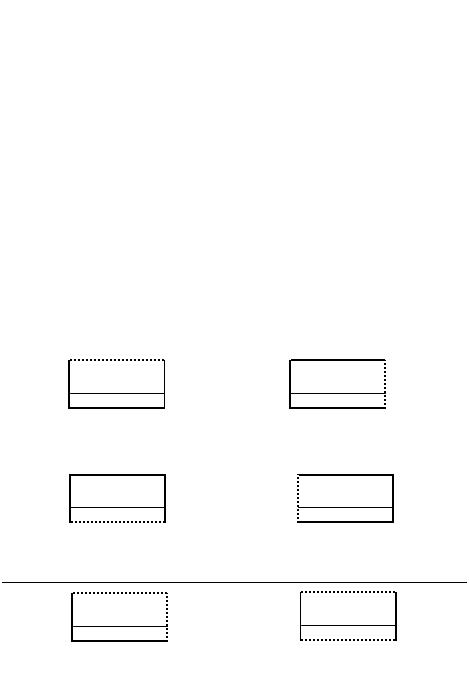
Варианты заданий (поперечные сечения волноводов)
LE-волны Вариант ¹1
LE-волны Вариант ¹2
LE-волны Вариант ¹3
LE-волны Вариант ¹4
LE-волны |
LE-волны |
Вариант ¹5 |
Вариант ¹6 |
20 |
Электродинамика и распространение радиоволн |
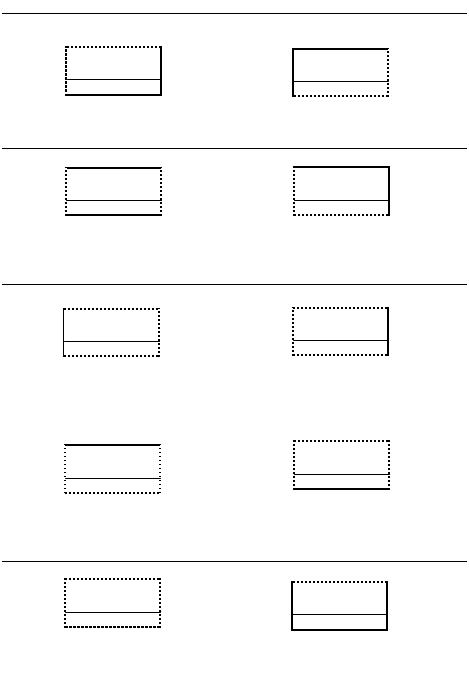
LE-волны Вариант ¹7
LE-волны Вариант ¹8
LE-волны Вариант ¹9
LE-волны Вариант ¹10
LE-волны |
LE-волны |
Вариант ¹11 |
Вариант ¹12 |
LE-волны |
LE-волны |
Вариант ¹13 |
Вариант ¹14 |
LE-волны |
LM-волны |
Вариант ¹15 |
Вариант ¹16 |
