примеры групп

Абстрактная алгебра – одна из наиболее важных и быстро развивающихся областей современной математики. Она занимается изучением свойств так называемых алгебраических операций, заданных на множествах произвольной природы, и строения множеств, наделенных алгебраическими операциями (алгебраических структур). Методы абстрактной алгебры находят применение в таких приложениях, как, например, теоретическая физика. Знание основ абстрактной алгебры необходимо для овладения идеями и методами современной математики.

Определение 4.1. Полугруппой называется множество, в котором определено действие, сопоставляющее каждой упорядоченной паре элементов третий – результат действия. Действие предполагается ассоциативным.

Примерами полугрупп могут служить: множество целых неотрицательных чисел относительно действия сложения, то же множество относительно действия умножения (другая полугруппа). В этих примерах действие коммутативно.

Например, любые два отображения одного и того же множества на себя можно выполнять последовательно, поэтому они образуют полугруппу.

Следовательно, все отображения множества на себя образуют полугруппу, которая называется полугруппой отображений данного множества.

Определение 4.2. Полугруппа называется группой, если в ней существует нейтральный элемент e такой, что при всех a из группы a*e=e*a=a (* - знак действия), и для каждого элемента a существует обратный a^-1, такой, что a*a^-1=a^-1*a=e.

Иными словами, упрощая, можно сказать, что на множествах можно задавать операции, обладающими тремя свойствами: 1) операция ассоциативна, то есть для любых трех элементов a, b и c выполняется соотношение (ab)c=a(bc); 2) существует единичный элемент e, что при любом a выполняется соотношение ea=ae=a; 3) существует обратный элемент, то есть для любого a можно найти такой однозначно определенный элемент a^-1, что aa^-1=a^-1a=e. Такая операция называется групповым умножением.

Примеры групп: группа всех целых чисел относительно сложения, группа положительных рациональных чисел относительно умножения. Эти группы коммутативны.

Далее будут приведены примеры числовых групп.

Коммутативные группы называются абелевыми.

Действие в группе обозначается обычно как умножение (мультипликативная запись), иногда как сложение (аддитивная запись). Аддитивная запись применяется только для абелевых групп. Нейтральный элемент при мультипликативной записи обозначается 1, при аддитивной 0. Соответственно, обратный к a элемент в мультипликативной записи обозначается a^-1, в аддитивной – через –a (называется противоположным элементом).

Введем понятие подгруппы. Если некоторое подмножество H множества элементов группы G само является группой относительно того же самого закона умножения, что и G, то группа H называется подгруппой группы G.

Для того, чтобы подмножество H было подгруппой группы G, необходимо и достаточно выполнение следующих двух условий: 1) подмножество H должно содержать вместе с любыми двумя своими элементами a и b их произведение ab; 2) подмножество H должно содержать вместе с любым своим элементом a, его обратный элемент a^-1. Смысл 1-го условия заключается в том, что закон умножения, определенный для группы G, является таковым и для подмножества H, так как, перемножая элементы этого подмножества, не выходим за его пределы. Ассоциативность умножения обеспечена тем, что умножение является таковым для группы G. В силу 2-го условия в подмножестве H для каждого элемента a существует обратный элемент a^-1; следовательно, в силу 1-го условия подмножество H содержит также aa^-1=e – единицу группы G. Указанные условия достаточны для того, чтобы подмножество H было подгруппой. Необходимость этих условий очевидна.

Приведем примеры подгрупп.

1. Найти подгруппу {4,6} аддитивной группы целых чисел. Элементами этой подгруппы в силу ее аддитивности являются числа вида 4k+6n,

где k и n – целые числа. Все числа – четные, так как их можно представить в виде 2(2k+3n). Выясним, все ли четные числа принадлежат данной подгруппе. Действительно, все, так как среди чисел вида 4k+6n содержится и число 2×2+6(-1)=2, следовательно, все элементы подгруппы, порожденной числом 2, то есть все четные числа. Значит, рассматриваемая подгруппа состоит из четных чисел.

2. Найти подгруппы {0} и {1} аддитивной группы целых чисел. Первая подгруппа состоит из кратных нуля. Так как любое число, кратное нулю, равно нулю, то эта подгруппа содержит только один элемент – нуль. Вторая подгруппа состоит из всех чисел, кратных 1, поэтому совпадает со всей аддитивной группой целых чисел. Следовательно, единица – единственный образующий элемент аддитивной группы целых чисел.

3. Описать подгруппу {(01),(02),(03),(04),(05),(06)} группы всех подстановок элементов 0,1,2,3,4,5,6. Любую подстановку можно представить в виде произведений транспозиций, перечисленных в фигурных скобках. Следовательно, подгруппа {(01),(02),(03),(04),(05),(06)} содержит все подстановки элементов 0,1,2,3,4,5,6.

Один-единственный элемент, выбранный из любой группы, порождает некоторую подгруппу. Такая подгруппа, порожденная одним элементом, называется циклической подгруппой.

Далее рассмотрим различные примеры групп. Здесь рассматриваются примеры множеств с различными операциями и выясняется, являются ли они группами или нет. На одних множествах чисел обычное умножение наделено всеми свойствами группового умножения, а на других – лишено их.

Пример 4.3. Целые числа. В множестве целых чисел умножение всегда выполнимо, то есть произведение любых двух целых чисел также является целым числом. Проверим, обладает ли оно тремя свойствами группового умножения.

1) Умножение ассоциативно. Действительно, умножение чисел обладает ассоциативностью. 2) Существует такое целое число e, что при любом целом числе a выполняется соотношение ea=ae=a. Это целое число e=1.

Замечание. Если e – такое число, что при любом отличном от нуля числе a выполняется соотношение ea=a, то это возможно лишь в одном случае: при e=1. С другой стороны, если рассматриваемое множество чисел содержит единицу, то все входящие в него числа удовлетворяют соотношениям 1a=a1=a. Следовательно, для множества чисел с обычным умножением в качестве предполагаемого группового умножения проверка свойства 2) сводится к ответу на вопрос, принадлежит ли единица к интересующему множеству. Единственное исключение составляет множество, содержащее только один элемент – нуль. 3) Обратный элемент не существует. Например, для числа 2 невозможно указать такое целое число x, которое удовлетворяло бы соотношению 2x=1, так как в левой части стояло бы четное, а в правой – нечетное число. Следовательно, целые числа не образуют группу по умножению: во множестве целых чисел деление выполнимо не во всех случаях. Значит, разумно рассматривать лишь такие множества чисел, в которых деление всегда выполнимо.

Пример 4.4. Рациональные числа. Так как произведение двух рациональных чисел – число рациональное, то обычное умножение не выводит за пределы множества рациональных чисел. 1) ассоциативность выполняется, единица – рациональное число. Убедимся, что на множестве рациональных чисел умножение обладает свойством 3). Если рациональное число (дробь) умножить на обратное число, то получится единица. Но для всякого ли рационального числа имеется обратное? Обратные числа существуют почти для всех рациональных чисел. Единственное исключение составляет нуль (при умножении на него всегда получается нуль). Следовательно, произведение двух сомножителей, один из которых равен нулю, не может быть равно единице. Поэтому в множестве рациональных чисел с заданным на нем умножением обратный элемент существует не для всех элементов. Таким образом, можно сформулировать правило: для выполнения условий 1)-3) необходимо (если определено умножение чисел), чтобы нуль не принадлежал рассматриваемому множеству. В частности, оно не должно состоять из одного лишь нуля. Следовательно, рациональные числа не образуют группу по умножению.

Пример 4.5. Рациональные числа, отличные от нуля. Произведение двух рациональных чисел, отличных от нуля, не равно нулю (как в примере 2) - рационально), умножение не выводит за пределы рассматриваемого множества чисел. Единица – рациональное число, отличное от нуля. Проверим свойство 3): для чисел, отличных от нуля, всегда существуют обратные числа, которые при умножении на данные числа дают единицу. Эти обратные числа также рациональны и отличны от нуля. Следовательно, отличные от нуля рациональные числа образуют группу по умножению.

Пример 4.6. Положительные рациональные числа. Проверим условие 3). Так как число, обратное положительному рациональному числу, также положительно и рационально, то условие выполнено. Следовательно, положительные рациональные числа образуют группу по умножению.

Пример 4.7. Числа +1 и –1. При умножении на +1 результат совпадает со вторым множителем, а (-1)´(-1)=+1. Следовательно, умножение не выводит за пределы рассматриваемого множества чисел. Проверим выполнение третьего условия. Умножение на множестве чисел +1 и –1 обладает свойством 3) группового умножения, так как каждое из этих двух чисел совпадает с обратным. Следовательно, числа +1 и –1 образуют группу по умножению.

Пример 4.8. Отрицательные рациональные числа. Так как произведение двух отрицательных рациональных чисел является положительным рациональным числом, то на множестве отрицательных рациональных чисел обычное умножение не может служить групповым умножением (умножение выводит за пределы множества отрицательных рациональных чисел). Следовательно, отрицательные рациональные числа не образуют группу по умножению.

Пример 4.9. Один лишь нуль. Так как 0´0=0, умножение не выводит из этого множества. Замечание об ассоциативности умножения остается в силе. Соотношение 0´0=0 показывает, что на множестве чисел, содержащем только нуль, умножение обладает свойствами 2) и 3). Следовательно, число 0 образует группу по умножению. Замечание. В примере 7 в роли единичного элемента выступает нуль. Элемент, соответствующий единичному, при умножении чисел называют единицей.

Теперь рассмотрим сложение чисел некоторых типов и установим в общем виде некоторые свойства сложения.

1. На множестве чисел сложение всегда ассоциативно.

2. Единица относительно сложения – это такой элемент e, который при любом элементе a, принадлежащем рассматриваемому множеству чисел, удовлетворяет соотношению e+a=a. Это условие выполняется лишь для нуля: при любом a нуль удовлетворяет условию 0+a=a+0=a. Следовательно, необходимо проверять, принадлежит ли нуль рассматриваемому множеству чисел.

3. Число, «обратное» числу a при сложении – число b, удовлетворяющее соотношению a+b=0. Такое число – это лишь b=-a. Для него условие

(-a)+a=a+(-a)=0 выполнено. Следовательно, достаточно проверять, содержит ли рассматриваемое множество чисел вместе с каждым принадлежащим числом то же число, взятое со знаком минус.

Рассмотрим множества чисел, на которых в качестве операции задано сложение.

Пример 4.10. Целые числа (сложение). Так как сумма двух целых чисел – целое число, то сложение не выводит за пределы рассматриваемого множества. Так как нуль – целое число и любое целое число, взятое со знаком минус, - также целое число, то сложение на множестве целых чисел обладает всеми свойствами группового умножения. Следовательно, целые числа образуют группу по сложению.

Пример 4.11. Рациональные числа. Сумма двух рациональных чисел – число рациональное; сложение не выводит за пределы множества рациональных чисел. Нуль – рациональное число. Любое рациональное число со знаком минус – также рациональное. Следовательно, сложение на множестве рациональных чисел обладает всеми свойствами группового умножения и рациональные числа образуют группу по сложению.

Пример 4.12. Рациональные числа, отличные от нуля. Множество по определению не содержит нуль, значит, сложение не обладает свойством 2). Следовательно, это множество не образует группу по сложению.

Пример 4.13. Положительные рациональные числа. Аналогично, не образуют группу по сложению.

Пример 4.14. Неотрицательные рациональные числа. К множеству из примера 4а присоединим нуль, тогда будет выполняться свойство 2):

сложение не выводит за пределы множества неотрицательных рациональных чисел, так как сумма их не может быть отрицательной, и она рациональна. Свойство 3) не выполняется, так как любое положительное рациональное число, взятое со знаком минус, становится отрицательным, а значит, не принадлежит множеству неотрицательных рациональных чисел. Следовательно, неотрицательные рациональные числа не образуют группу по сложению.

Пример 4.15. Числа +1 и –1, Пример 6а. Отрицательные рациональные числа. Указанные множества не содержат нуля, следовательно, не образуют группу по сложению.

Пример 4.16. Один лишь нуль. Так как 0+0=0, то сложение не выводит за пределы рассматриваемого множества. Остальные условия также выполняются. Следовательно, число 0 образует группу по сложению.

1* Непустое множество Â преобразований некоторого множества M является группой, если: а) вместе с двумя любыми преобразованиями оно содержит их произведение и б) вместе с каждым преобразованием содержит обратное к нему. (доказать самостоятельно)

2* Повороты плоскости вокруг фиксированной точки P образуют абелеву группу. Но если к этому добавить еще и отображения относительно всех прямых, проходящих через точку P, то получится уже неабелева группа.

3* Доказать, что элементы e, a с законом композиции ee=e, ea=a, ae=a, aa=e образуют (абелеву) группу.

*Задача повышенной трудности. Подмножество элементов группы.

Пусть G – абелева группа и A – подмножество, содержащее n ее элементов и такое, что из aÎA следует a^-1ÏA. Рассмотрим n² (не обязательно различных) элементов группы G вида a_ia_j, где a_i,a_j принадлежит подмножеству A.

Доказать, что не более этих элементов принадлежат подмножеству A.

(Leo Moser)

Решение. Для каждого элемента a_ia_j=a_k из A существует элемент a_ka_j^-1=a_i, также принадлежащий подмножеству A. Следовательно, в подмножестве A число элементов вида a_ia_j совпадает с числом элементов вида a_ia_j^-1. Рассмотрим n² элементов вида a_ia_j^-1. Из свойств подмножества A следует, что единичный элемент I=a_ia_i^-1 не принадлежит A и элемент

a_ja_i^-1=(a_ia_j^-1)^-1 не принадлежит A, если A, содержит элемент a_ia_j^-1. Таким образом, подмножество A содержит не более 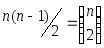элементов вида

a_ia_j^-1. Это означает, что число элементов вида a_ia_j в A также не превышает .ž

Определение 4.3. Если данная группа порождена одним элементом, то она называется циклической группой.

Если a – элемент группы, то подгруппа {a} состоит из всех различных степеней элемента a. Следовательно, число элементов в подгруппе {a} совпадает с порядковым номером.

Определение 4.4. Кольцом называется множество математических объектов, в котором определены два действия – «сложение» и «умножение», сопоставляющее упорядоченным парам элементов их «сумму» и «произведение», являющиеся элементами того же множества.

Действия удовлетворяют следующим аксиомам:

1.(a+b)+c=a+(b+c) (ассоциативность сложения)

2. a+b=b+a (коммутативность сложения)

3. Существует нулевой элемент 0 такой, что a+0=a при любом a.

4. Для каждого a существует противоположный –a такой, что a+(-a)=0.

5. (a+b)c=ac+bc

5’. с(a+b)=ca+cb (левая и правая дистрибутивность)

6. (ab)c=a(bc) (ассоциативность умножения). При выполнении этого требования элементы кольца образуют полугруппу относительно умножения.

7. ab=ba (коммутативность умножения)

8. Существование единичного элемента 1 (то есть такого, что a*1=1*a=a для любого элемента a).

9. Существование обратного элемента a^-1 для любого элемента a, отличного от 0.

Замечание.

1. Первые четыре требования означают, что элементы кольца образуют абелеву группу относительно сложения, которая называется аддитивной группой кольца.

2. Определение 4.5. Кольцо называется ассоциативным, если в нем выполнено условие 6, коммутативным, если выполнено условие 7, коммутативным и ассоциативным, если выполнены условия 6 и 7. Если выполнено условие 8, говорят о кольце с единицей.

Приведем примеры колец.

1. Кольцо четных чисел. На множестве четных чисел принято рассматривать сложение и умножение. Четные числа образуют группу по сложению. По умножению они образуют полугруппу, так как произведение двух четных чисел - число четное, а умножение ассоциативно. Так как сложение и умножение четных чисел связаны законом дистрибутивности (закон выполняется для любых трех чисел), то получаем кольцо (коммутативное кольцо).

2. Кольцо рациональных чисел. Рациональные числа образуют группу по сложению и полугруппу по умножению. Так как на множестве рациональных чисел сложение и умножение связаны законом дистрибутивности, получим коммутативное кольцо.

3. Кольцо действительных (вещественных) чисел.

4. Кольцо многочленов с целочисленными коэффициентами. Сначала дадим некоторые определения.

Определение 4.6. Выражения вида

, где - целые числа, называются многочленами с целочисленными коэффициентами.

Члены многочлена можно записать в обратном порядке: .

Определение 4.7. Говорят, что многочлен f(x) совпадает с многочленом , если равенства b₀=a₀, b₁-a₁,…, выполняются до тех пор, пока существуют как коэффициенты b_i, так и коэффициенты a_i; если какой-либо из коэффициентов a_i или b_i не существует, то коэффициент другого многочлена с тнм же номером либо также не существует, либо равен нулю. Например, многочлены 2+3x и 2+3x+0x² совпадают.

Определение 4.8. Суммой h(x)=f(x)+g(x) многочленов f(x) и g(x) называется многочлен .

Замечание. n³k, и в многочлене g(x) «отсутствующие» коэффициенты заменены нулями.

Относительно определенной таком образом операции сложения, многочлены образуют коммутативную группу, так как при любом xⁱ может стоять произвольное целое число, а целые числа образуют кольцо.

Определение 4.9. Произведением k(x)=f(x)g(x) многочленов f(x) и g(x) называется многочлен

.

Введенная операция умножения ассоциативна. Следовательно, многочлены образуют полугруппу (коммутативную). Не доказывая, отметим, что заданные на множестве многочленов с целочисленными коэффициентами операции сложения и умножения связаны законом дистрибутивности. Следовательно, многочлены с целочисленными коэффициентами образуют коммутативное кольцо.

5. Кольцо многочленов с рациональными коэффициентами.

6. Кольцо многочленов с действительными (вещественными) коэффициентами.

7. Рассмотрим пары вещественных чисел (a,b). Причем, пары (a,b) и (c,d) считаем равными только в том случае, когда a=c и b=d. Определим сложение пар с помощью тождества (a,b)+(c,d)=(a+c, b+d), а умножение –

при помощи тождества (a,b)(c,d)=(ac, bd) Пары вещественных чисел образуют коммутативную группу относительно заданной на них операции сложения. Это следует из того, что операция сложения совпадает с операцией сложения, определенной на прямом произведении двух вещественных прямых. (Аналогично проводятся рассуждения для умножения). Умножение пар ассоциативно, так как операция, производимая над каждой компонентой пар, ассоциативна; умножение пар вещественных чисел коммутативно. Проверим дистрибутивность:

[(a,b)+(c,d)](e,f)=(a+c, b+d)(e,f)=([a+c]e, [b+d]f), с другой стороны, (a,b)(e,f)+(c,d)(e,f)=(ae, bf)+(ce, df)=(ae+ce, bf+df). Элементы, стоящие в правых частях последних равенств, совпадают в силу дистрибутивности сложения чисел по умножению. Итак, пары вещественных чисел образуют коммутативное кольцо.

Теперь можно уточнить определение кольца.

Определение 4.10. Кольцом называется тройка <R;f,g>, где R – некоторое множество; <R;f> - коммутативная группа, <R;g> - полугруппа, и для любых трех элементов a,b,c множества R операции f и g связаны соотношениями g(f(a,b),c)=f(g(a,c),g(b,c)) и g(c, f(a,b))=f(g(c,a),g(c,b)). Операция f задает в кольце «сложение» (+), а g – «умножение» (·).

Определение 4.11. Два элемента кольца, произведения которых равно нулю, хотя каждый из сомножителей отличен от нуля, называются делителями нуля. Если кольцо не содержит делителей нуля, то оно называется кольцом без делителей нуля.

Кольцо целых чисел, кольцо многочленов не содержат делителей нуля и коммутативны. Чтобы подчеркнуть сходство коммутативных колец

без делителей нуля с кольцом целых чисел, их называют областями целостности. Итак,

Определение 4.12. Кольцо называется областью целостности, если из равенства ab=0 следует, что хотя бы один из сомножителей a или b равен 0.

Определение 4.13. Кольцо, в котором для всех элементов существуют обратные, состоит только из нуля и называется нулевым кольцом.

Определение 4.14. Кольца, в которых для всех отличных от нуля элементов существуют обратные, называются телами.

Тела не содержат делителей нуля. Если тело коммутативно, то оно является областью целостности. Тело не является группой относительно умножения, так как обратные элементы существуют только для элементов, отличных от нуля.

Приведем примеры тел.

1. Тело рациональных чисел. Рациональные числа образуют кольцо. Удостоверимся, что это кольцо является телом, для чего покажем, что для всех, отличных от нуля рациональных чисел существуют обратные числа. Это очевидно, так как всякое рациональное число можно представить в

виде a/b (a,b - целые) и если оно отлично от нуля, то a¹0 и поэтому существует такое рациональное число b/a, для которого (a/b)(b/a)=1.

Замечание. Важно, чтобы обратный элемент принадлежал тому же кольцу, которому принадлежит исходный элемент. Например, целые числа не образуют тела, хотя для любого отличного от нуля целого числа существует обратное, но, как правило, оно не целое.

2. Тело действительных (вещественных) чисел. Действительные числа образуют кольцо, так как для любого отличного от нуля действительного числа в множестве действительных чисел существует обратное. (Здесь точно не определили действительное число, поэтому доказательство опустим).

*Задача повышенной трудности. Кольцо с делением. Элемент кольца x называется правым квазирегулярным, если существует элемент y того же кольца, такой, что x+y+xy=0. Доказать обратное утверждение: если в кольце A каждый элемент, кроме одного, правый квазирегулярный, то A – кольцо с делением.

(Irving Kaplansky)

Решение. Пусть e – единственный исключительный элемент. Ясно, что e¹0. а) Так как при всех y: e+(-e+y-ey)+e(-e+y-ey)=-e²+y-e²y¹0, то –e²=e, или

e²+e=0. б) Соотношение x+xe=0 выполняется при всех x. Действительно, если бы выполнялось соотношение e+x+ex¹0, то существовал бы элемент кольца y, такой, что e+x+ex+y+(e+x+ex)y=0. Умножая последнее соотношение слева на e, получаем (по доказанному в п.»а») e²=0, или e=0. Полученное противоречие доказывает, что соотношение x+ex=0 выполняется при всех x. Аналогично полученный результат позволяет доказать, что x+xe=0 также при всех x. Таким образом, -e совпадает с единичным элементом кольца A. в) соотношение x+y+xy=0 можно представить в виде (x-e)(y-e)=-e при x¹e, или XY=-e при X¹0, где X=x-e, Y=y-e. Таким образом, для любого отличного от 0 элемента X кольца A существует обратный элемент. Следовательно, A – кольцо с делением.

4.* Определение 4.15. Полем называется коммутативное ассоциативное кольцо с единицей, в котором каждый отличный от нуля элемент a имеет обратный a^-1. То есть, поле – это кольцо, в котором отличные от нуля элементы образуют коммутативную группу. Эта группа называется мультипликативной группой поля.