Konspekt_SM_3

Угол наклона нейтральной линии найдем по формуле (16.5):

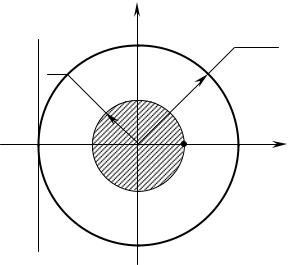
Зная напряжение в точках А и С и равенство нулю σ на нейтральной линии, строим эпюру σ (см. рис. 16.7).

4 Определяем положение нейтральной линии. Она проходит через центр тяжести сечения и через II и IV квадранты (рис.16.8).

Рисунок 16.8

PDF created with pdfFactory Pro trial version www.pdffactory.com

17 СЛОЖНОЕ СОПРОТИВЛЕНИЕ (продолжение)

17.1 Внецентренное растяжение и сжатие

Рассмотрим частный случай сложного сопротивления, когда брус растягивается (или сжимается) силами, параллельными оси бруса, так, что линия действия равнодействующей не совпадает с осью бруса (рис.17.1, а).

Рисунок 17.1

Вид нагружения, при котором равнодействующая внешних сил не совпадает с осью стержня, а смещена относительно его оси и остается ей параллельна, называется внецентренным растяжением или сжатием.

Точка приложения равнодействующей Р называется полюсом силы. Пусть точка приложения внешних сил имеет координаты хp, уp. При

такой нагрузке в любом поперечном сечении бруса действуют продольная сила N = P и изгибающие моменты (см. рис.17.1, б):

M x = Pхp ; M y = Pуp .

Таким образом, внецентренное растяжение-сжатие оказывается идентичным косому изгибу. В отличие от последнего, однако, в поперечном сечении бруса возникают не только изгибающие моменты, но и продольная сила N = P .

В произвольной точке с координатами x, y нормальное напряжение σ будет складываться из напряжений осевого растяжения (сжатия) силой N и напряжений от чистого изгиба моментами M x , M y :

PDF created with pdfFactory Pro trial version www.pdffactory.com

Очевидно, пространственная эпюра образует плоскость (поскольку входят в уравнение в первой степени), не проходящую через центр тяжести

Переменными в формулах (17.1) и (17.2) являются два последних слагаемых, отражающих влияние изгиба. Так как при изгибе наибольшие напряжения будут в точках, наиболее удаленных от нейтральной линии, то, как и при косом изгибе, надо отыскивать положение нейтральной линии.

Обозначим координаты точки, принадлежащей нейтральной линии, через

x0 , y0 - координаты точек на нейтральной линии.

Уравнение (17.3) представляет собой уравнение нейтральной линии, из которого видно, что нейтральная линия не проходит через центр тяжести сечения.

Чтобы построить эту прямую, проще всего вычислить отрезки, отсекаемые ею на осях координат. Обозначим эти отрезки xн и yн (рис.17.2).

Чтобы найти отрезок xн , отсекаемый на оси Ох, надо в уравнении (17.3) положить xo = xн , yo = 0 .

PDF created with pdfFactory Pro trial version www.pdffactory.com

Тогда получим

1 + xpi2× xн = 0 .

y

i 2

Откуда xн = − xy . (17.4) p

Аналогично, полагая x0 = 0 , y0 = yн , получим

расположена в квадранте, противоположном тому, в котором находится точка приложения внешней силы.

Теперь, проводя параллельно нейтральной линии касательные к контуру сечения, найдем наиболее напряженные точки А и В в растянутой и сжатой зонах сечения и построим эпюру нормальных напряжений σ (см. рис 17.2).

PDF created with pdfFactory Pro trial version www.pdffactory.com

Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр и др.), координаты x, y угловых точек одновременно достигают максимальных значений. Поэтому формулы (17.6) и (17.7) можно записать в виде:

17.2 Ядро сечения

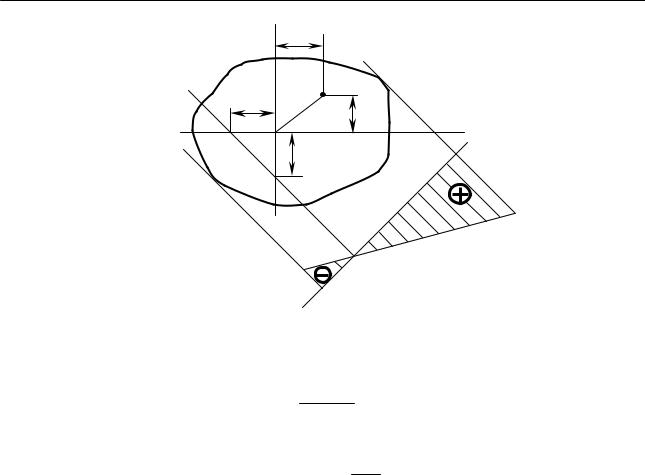
Нейтральная линия в общем случае может проходить как через поперечное сечение, так и вне его. Действительно, если сила Р приложена в центре тяжести (хр = ур = 0), то, согласно формулам (17.4) и (17.5), нейтральная линия проходит в бесконечности, и напряжения в этом случае распределены по сечению равномерно. По мере увеличения эксцентриситета е нейтральная ось будет приближаться к центру тяжести сечения. Конструктору желательно знать заранее, какой эксцентриситет при выбранном типе сечения можно допустить, не рискуя вызвать в сечении стержня напряжений разных знаков. Это важно знать при конструировании стержней из материалов, по- разному работающих на растяжение и сжатие. Представляет интерес установить область таких удалений силы Р от оси, при которых эпюра нормальных напряжений по сечению остается однознаковой.

Ядром сечения называется область вокруг центра тяжести сечения, приложение силы Р внутри которой вызывает во всем поперечном сечении напряжения одного знака.

Для построения ядра сечения необходимо задаваться различными положениями нейтральной оси и вычислить соответствующие точки приложения силы Р по формулам, вытекающим из уравнений (17.4) и (17.5):

Вычисленные координаты xp, yp определяют точки, лежащие на границе ядра сечения (рис.17.3).

PDF created with pdfFactory Pro trial version www.pdffactory.com

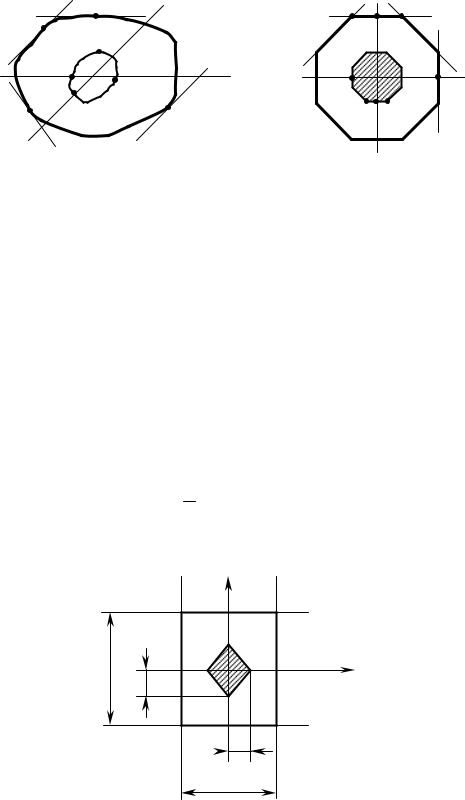
При повороте нейтральной линии вокруг некоторой неподвижной точки контура сечения точка приложения силы перемещается вдоль некоторой кривой, так как xp, yp и x, y связаны линейно (см. рис.17.3, а). Для построения ядра сечения какого-либо многоугольника необходимо проводить касательные, совпадающие с его сторонами. Ядро сечения будет повторять форму поперечного сечения (см. рис.17.3, б).

Построим ядро сечения для прямоугольника (рис.17.4) со сторонами b и h.Совместим вначале нейтральную линию с одной из сторон прямоугольника (положение I–I). При этом координаты нейтральной линии равны

PDF created with pdfFactory Pro trial version www.pdffactory.com

Аналогично определяем координаты точек 3’ и 4’.

Так как при переходе нейтральной линии с одной стороны на другую она поворачивается вокруг угловой точки сечения, то точка приложения силы перемещается по прямой, образуя контур ядра. Таким образом, ядро сечения прямоугольника будет ромбом с диагоналями, равными одной трети соответствующей стороны сечения.

PDF created with pdfFactory Pro trial version www.pdffactory.com

В круге все центральные оси – главные. Поэтому при касании нейтральной линии I–I в любой точке окружности точка 1’ ядра сечения будет

лежать на том же диаметре с противоположной стороны относительно центра тяжести.

Положение нейтральной линии определяется координатами:

xн = −R; yн = ∞ .

Тогда координаты точки 1’ ядра:

y p = 0 .

Таким образом, очертание ядра – круг радиуса d8 или R4.

Рассмотрим пример нагружения стержня внецентренно приложенной силой. Определим напряжения в точках А, В, С и D стержня нагруженной силой Р=400 кН (рис.17.6). Размеры сечения (в сантиметрах) даны на рисунке. Определить также положение нейтральной линии.

PDF created with pdfFactory Pro trial version www.pdffactory.com

2 Рассмотрим действие силы Р на каждую угловую точку сечения и

расставим знаки отдельных слагаемых выражения σ (см рис.17.6, б).

3 Определим напряжения в точках A, B, C и D, учитывая знаки соответствующих напряжений (N, Mx, My):

Покажем положение нейтральной линии на сечении (см. рис.17.6, б).

PDF created with pdfFactory Pro trial version www.pdffactory.com

18 СЛОЖНОЕ СОПРОТИВЛЕНИЕ (продолжение)

18.1 Изгиб с кручением круглых валов

При рассмотрении кручения предполагалось, что в поперечных сечениях круглого стержня возникает только крутящий момент. Однако такие детали машин, как валы, редко работают на чистое кручение. Даже прямой вал при работе изгибается собственным весом, весом шкивов, натяжением ремней и т.д. Таким образом, большинство скручиваемых элементов машин работают на совместное действие изгиба и кручения.

При действии изгиба и кручения в поперечных сечениях вала возникает пять внутренних силовых факторов: крутящий момент Мкр, изгибающие моменты Мх и Му, поперечные силы Qx и Qy.

Таким образом, в любом поперечном сечении одновременно возникают нормальные напряжения от изгиба в двух плоскостях, а также касательные напряжения от изгиба и кручения. Для расчета вала в первую очередь должны быть построены эпюры изгибающих моментов Мх, Му и крутящего Мкр=Мz. Для этого нагрузки, действующие на вал, раскладываем на составляющие вдоль координатных осей, а затем строим эпюры:

–изгибающих моментов относительно вертикальной оси (Му) от горизонтальных проекций Р1х, Р2х,…, Pnx;

–изгибающих моментов относительно горизонтальной оси (Мх) от вертикальных проекций P1y, P2y,…, Pny;

–крутящих моментов (МКР).

Рассмотрим расчет вала на примере (рис.18.1).

Разложим нагрузки на горизонтальные и вертикальные плоскости и строим эпюры изгибающих моментов Mx и My (см. рис.18.1, г и е). Имея эти эпюры, можем для каждого сечения вала найти полный изгибающий момент Мизг (см.рис.18.1, ж), как геометрическую сумму обеих составляющих

Mизг = 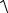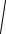M x2 + M y2 .

Для каждого сечения мы будем иметь свою плоскость изгибающего момента, но так как вал имеет круглое поперечное сечение, у которого моменты сопротивления относительно всех центральных осей одинаковы, то без влияния

на результаты расчета мы можем совместить плоскости изгибающих моментов для осей сечений и построить суммарную эпюру Мизг, располагая ее в плоскости чертежа. Так как суммарный момент в разных сечениях может иметь разные направления, то даже при отсутствии распределенных нагрузок эпюра Mизг может быть криволинейной.

PDF created with pdfFactory Pro trial version www.pdffactory.com