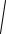Konspekt_SM_3
.pdf
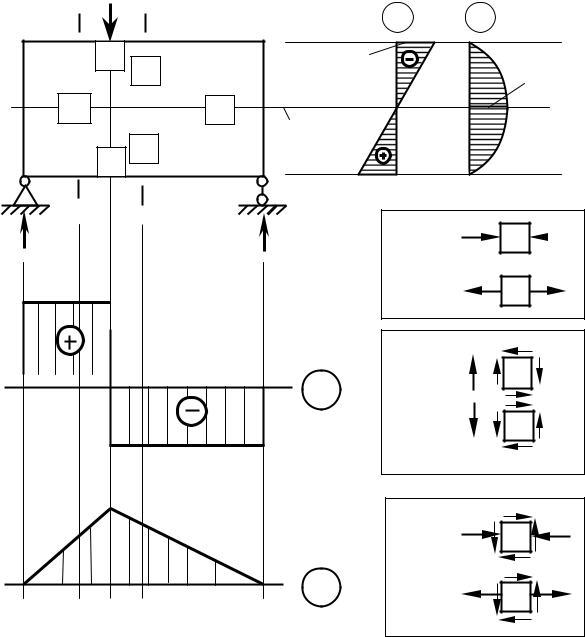
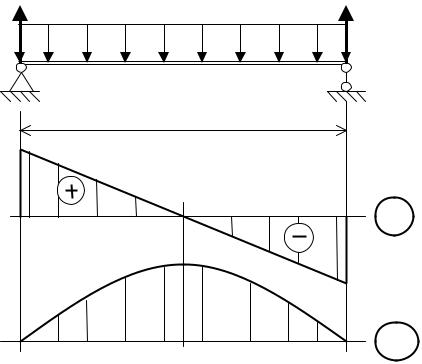

15.2 Примеры расчета балки по основному условию прочности |
137 |
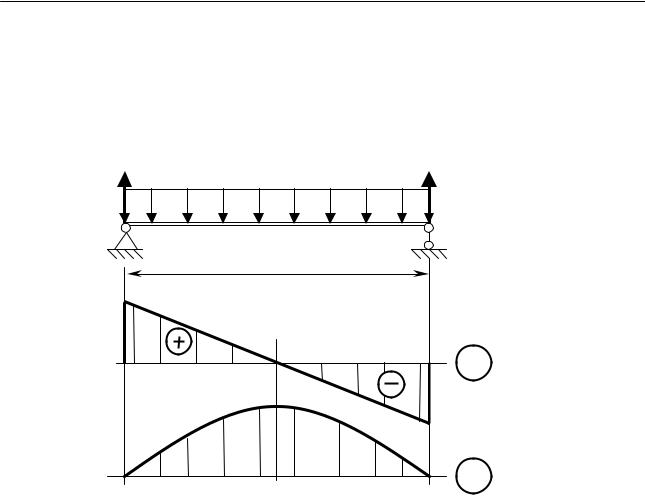
Опасным будет сечение посередине пролета, где |
Мmax=20 кН·м. |
Опасными будут точки этого сечения, наиболее удаленные от нейтральной линии. Условие прочности для них следующее:
σ max = |
|
M max |
= |
20 ×10−3 |
|
£ 160 Þ Wxр ас ³ |
20 ×10−3 |
|
×106 = 125 см3 . |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
Wx |
|
160 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
Wx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
круга |
|
|
W = |
π × D3 |
|
= 0,1D3 ³ 125 Þ D ³ 3 |
|
= 10,83 см, |
||||||||||||||||||||||||||||
|
Для |
|
|
|
|
|
1250 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
принимаем D=11 см =110 мм. Тогда Wкр=0,1·113=130,5 см3. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
σ рас - [ σ ] |
|
|
|
|
|
|
|
|
M max |
|
- |
M max |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
δ σ |
= |
|
× 100 % = |
|
|
|
W |
|
|
W р ас |
|
|
= |
|
|
Wmax |
- W р ас |
. |
|||||||||||||||||||||||
|
|
|
[ σ ] |
|
|
|
|
|
|
|
|
M max |
|
|
|
|
|
|
|
W р ас |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M р ас |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для прямоугольника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
bh2 |
|
|
h |
|
|
|
|
|
b ×( 4b2 ) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Wx = |
|
= |
= 2 |
= |
= |
b |
3 |
³ 125 Þ b ³ 3 |
125×3 |
=5,72см. |
|
||||||||||||||||||||||||||||||
6 |
|
b |
|
|
|
6 |
|
|
3 |
|
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
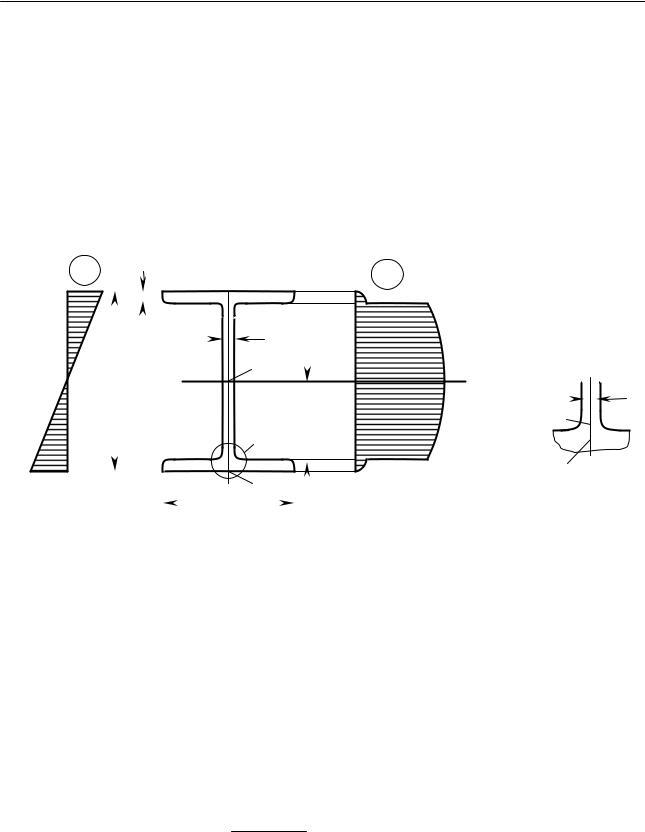
Для двутавра принимаем №18, Wx=148 см2 (ГОСТ 8239 - 89).
Рассмотренный выше пример расчета на прочность при изгибе относится к тому случаю, когда опасной точкой является одна из точек крайних волокон балки и напряженное состояние в ней линейное. В подавляющем большинстве случаев этого расчета достаточно. Однако встречаются случаи, когда опасная точка будет принадлежать нейтральному сечению. В этой точке материал испытывает чистый сдвиг, и для расчета следует пользоваться условием
прочности по касательным напряжениям
τ max = |
Qmax Sxmax |
£ [τ ]. |
|
bI x |
|||
|
|
Такое положение может иметь место тогда, когда при больших поперечных силах в сечениях балки действуют незначительные изгибающие моменты.
PDF created with pdfFactory Pro trial version www.pdffactory.com