Валишвили В.З. ЭТК-112

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Московский государственный университет путей сообщения (МИИТ)

Институт Экономики и Финансов

Кафедра «Математика»

Реферат

По дисциплине «Математика»

Тема: «Задача Дирихле»

Выполнил: студент группы ЭТК-112 Валишвили В.З.

Проверила: старший преподаватель Сирош М.М.

МОСКВА 2014

Оглавление

Введение 3

Постановка задачи 3

Описание метода решения поставленной задачи 4

Графики решений 5

Связанные теоремы 7

Аналитическое решение 7

Численное решение 7

Физическая интерпретация 8

Вывод 8

Введение

Задача Дирихле — вид задач, появляющийся при решении дифференциальных уравнений в частных производных второго порядка. Названа в честь Иоганна Дирихле.

Постановка задачи

Задача Дирихле ставится следующий образом: пусть в области  задано уравнение

где  — оператор Лапласа. С краевыми условиями:

Такая задача называется внутренней задачей Дирихле или первой краевой задачей. Сами условия называются условиями Дирихле или первыми краевыми условиями. Второе называние может трактоваться шире, обозначая любую задачу решение дифференциального уравнения, когда известно значение искомой функции на всей границе области. В случае, когда надо найти значения функции вне области  задача называется внешней задачей Дирихле.

Решить численно задачу Дирихле для уравнения Лапласа:

(x,y) D; u|_Г=xy²=f(x,y);

область D ограничена линиями: x=2 , x=4 , y=x , y=x+4 ;

(x₀, y₀ ) = (3, 5) .

Следует решить задачу сначала с шагом по x и по y : h=0.2, потом с шагом h=0.1 . Точность решения СЛАУ =0.01.

Описание метода решения поставленной задачи

Поставленная задача решается численно с помощью программы, реализующей метод сеток , разработанный для численного решения задачи Дирихле для уравнений эллептического типа.

Программа написана на языке C++ , в среде Borland C++ версии 3.1. Ниже описан алгоритм работы этой программы.

1. На первом шаге область D дискретизируется. Она заменяется на область D_h путем разбиения области D параллельными прямыми по следующему правилу: y_i=y₀  ih, x_j=x₀  ih , i,j=0,1,2…. PР. Разбиение производится до тех пор, пока текущая прямая не будет лежать целиком вне области D. Получается множество точек (x_i,y_j).

2. За область D_h принимают те точки множества (x_i,y_j) , которые попали внутрь области D, а также дополняют это множество граничными точками.

3. Во всех точках области D_h вычисляются значения функции f(x_i,y_j) .

4. За область D_h* принимаются все внутренние точки области D_h, т.е. удовлетворяющие требованию:

(x_i,y_j) D_h* , если (x_i+1,y_j)  D_h , (x_i-1,y_j) D_h , (x_i,y_j+1) D_h , (x_i,y_j-1) D_h .

5. Во всех точках области D_h* вычисляется функция F_(N)*[i,j] ( индекс N обозначает номер итерации, на которой производится вычисление):

F_(N)*[i,j]=(f(x_i+1,y_j) + f(x_i-1,y_j) + f(x_i,y_j+1)f(x_i,y_j-1))/4

6. Теперь если max | F_(N+1)*[i,j] - F_(N)*[i,j]|< ,взятый по всем точкам области D_h* ,то задача решена;

если нет , то выполнять шаг 5 ( пересчитывать функцию F_(N)*[i,j] через значения F_(N-1)*[i,j]) до тех пор, пока не выполнится указанное условие.

Графики решений

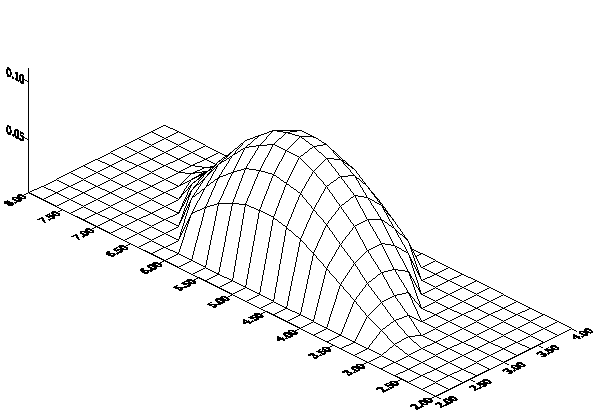
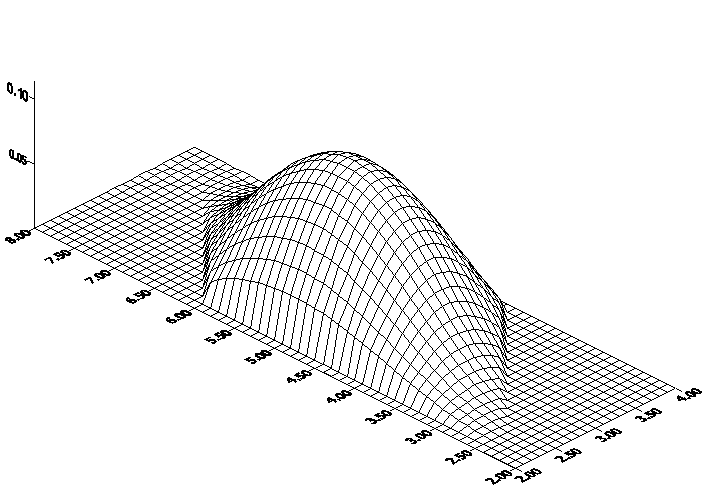
Связанные теоремы

Теорема. Решение задачи Дирихле, внутренней или внешней, единственно.

Аналитическое решение

Аналитически задача Дирихле может быть решена с помощью теории потенциала. Решение однородного уравнения можно представить в виде:

,

где  — функция Грина для оператора Лапласа в области .

Численное решение

Построение аналитического выражения для функции Грина в сложных областях может вызвать затруднения, поэтому для решения таких задач приходится пользоваться численными методами. Для каждого метода свои особенности учёта первых краевых:

• В методе конечных разностей для узлов на границе области записывается уравнение , где 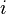 — номер соответствующего узла.

• В методе конечных элементов такие краевые условия называют главными краевыми условиями и они учитываются на этапе сборки матрицы, для всех весов связанных с границей уравнения заменяются на уравнения вида 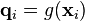, далее выполняется несколько шагов методом Гаусса, чтобы полученная матрица была симметричной.

Физическая интерпретация

Физическая интерпретация условий Дирихле — поведение искомой величины на границе:

• Температура, если рассматривается уравнение теплопроводности

• После скорости, если рассматривается уравнение Стокса

• Магнитное поле или электрическое поле, если рассматривается некоторое уравнение, получаемое из уравнений Максвелла (тогда краевые условия называют магнитными или электрическими краевыми условиями, соответственно).

Вывод

Функция f(x,y) является неотрицательной в области D. Полученное решение лежит целиком над плоскостью XOY . Для данного решения выполняется принцип максимума.

	Страница 8