3283

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Электроснабжение железнодорожного транспорта»

ОСНОВЫ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ

Методические указания к выполнению практических работ для студентов специальности 190901.65 – Системы обеспечения движения поездов (ЭС)

очной и заочной форм обучения

Составитель: В.А. Загорский

Самара

2013

1

УДК 621.311

Основы технической диагностики : методические указания к выполнению практических работ для студентов специальности 190901.65 – Системы обеспечения движения поездов (ЭС) очной и заочной форм обучения / составитель В.А. Загорский. – Самара : СамГУПС, 2013. – 39 с.

В настоящих методических указаниях по дисциплине «Основы технической диагностики» приведены теоретические материалы, методика, иллюстрации и табличные данные, необходимые для выполнения диагностики технического состояния объектов системы электроснабжения железнодорожного транспорта. Методические указания предназначены для студентов специальности 190901.65 «Системы обеспечения движения поездов» специализация «Электроснабжение железных дорог».

Утверждены на заседании кафедры от 31.05.2013 г., протокол № 10. Печатаются по решению редакционно-издательского совета университета.

Составитель: д.т.н., профессор Загорский Владимир Алексеевич

Рецензенты: к.т.н., доцент СамГУПС В.Б. Тепляков; к.т.н., профессор СамГУПС Л.С. Лабунский

Под редакцией составителя Компьютерная верстка: Е.А. Самсонова

Подписано в печать 05.09.2013. Формат 60×90 1/16. Усл. печ. л. 2,4. Тираж 100 экз. Заказ 161.

© Самарский государственный университет путей сообщения, 2013

2

СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА

ПРАКТИЧЕСКАЯ РАБОТА № 1

Вероятность и частота. Совместимые и несовместимые события. Правила теории вероятности. Условная вероятность. Решение задачи о выборе исправного элемента (2 часа)

Цель работы: изучить отдельные понятия и правила теории вероятности.

ВЕРОЯТНОСТЬ И ЧАСТОТА. СОВМЕСТИМЫЕ И НЕСОВМЕСТИМЫЕ СОБЫТИЯ

При испытании 20 изоляторов в 10 случаях произошел их пробой. Необходимо оценить частоту событий пробоя изоляторов и вероятность их пробоя. Число испытаний обозначим как N, а число пробоев как n. Очевидно, что пробой изоляторов является случайным событием. Дадим определение частоты случайных событий.

Частотой случайных событий Рч называется отношение числа произошедших случайных событий n к числу опытов N:

Рч = n / N.

В рассматриваемом нами случае Рч = 10 / 20 = 0,5.

Если серию опытов проводит многократно, то будут получаться некоторые значения, которые колеблются около некоторого значения Р, приближаясь к нему по мере увеличения числа опытов. Тогда можно записать:

lim Рч = Р при N → ∞.

Величина Р называется вероятностью случайного события.

Поскольку для определения вероятности события необходимо произвести бесконечное число испытаний, то экспериментально величина Р получена быть не может, а может быть получено только близкое к ней значение величины частоты случайного события Рч. При проведении экспериментов, для простоты считают, что Рч = Р и говорят не о частоте случайного события, а о его вероятности.

При проведении испытаний получаются различные результаты, которые называются несовместимыми или совместимыми событиями.

3

События называются несовместимыми, если они не могут появиться одновременно.

События называются совместимыми, если они могут появиться одновременно.

Два и более несовместимых события образуют полную группу событий, если в результате опыта обязательно должно произойти хотя бы одно из них.

Примеры

Опыт с монетой. Обязательно должно произойти хотя бы одно из двух событий – монета упадет орлом или решкой. Полную группу событий составляет два несовместимых события.

Опыт с кубиком. Обязательно должно произойти хотя бы одно из 6 событий – выпадет цифра от 1 до 6. Полную группу событий составляет 6 несовместимых события.

Опыт с двумя кубиками. Одинаковая цифра может появиться на обоих кубиках. Появление одинаковых цифр на обоих кубиках является совместимыми событиями.

ПРАВИЛА ТЕОРИИ ВЕРЯТНОСТИ

Правило № 1. Вероятность полной группы событий равна 1.

Следствие. Если Р(А) – вероятность появления события А, а Р(В) – вероятность его непоявления, то:

Р(А) = 1 – Р (В).

Пример. Вероятность события Р(А) = 0,8. Тогда вероятность того, что событие А не произойдет: Р(В) = 1– 0,8 = 0,2.

Правило № 2. Если А и В – два независимых события, то вероятность того, что произойдут оба этих события, называется вероятностью их совместного появления.

Вероятность появления двух независимых событий равна произведению вероятностей этих событий:

Р(А и В) = Р(АВ) = Р(А) ·Р(В).

Пример. Определить вероятность выпадения одинаковых цифр на двух кубиках с шестью гранями.

Решение. Вероятность выпадения какой-либо цифры на первом кубике (появление события А) составляет Р(А) = 1/6. Вероятность выпадения какой-либо цифры на втором кубике (появление события В) составляет Р(В) = 1/6. Вероятность совместного появления двух независимых событий составляет: Р(А и В) = Р(АВ) = Р(А) ·Р(В) = 1/6 · 1/6 = 1/36.

4

Правило № 3. Вероятность совместного появления каждого из N независимых событий А1, А2, А3, … Аn равна произведению вероятностей появления каждого из этих событий в отдельности:

Р (А1 и А2 и А3 и… Аn) = .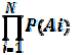

Пример. Бросали3 монеты. Определитьвероятностьтого, чтовсетриупалиорлом. Решение. Вероятность выпадения орла на каждой из монет одинакова и составляет

Р(А1) = Р(А2) = Р(А3) = 0,5. Вероятность совместного появления трех этих событий Р (А1 и А2 и А3) = 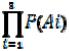= 0,5 · 0,5 · 0,5 = 0,125.

Проверка. Полная группа событий выпадения трех монет орлами или решками составит 8 возможных сочетаний:

О О О; О О Р; О Р О; О Р Р; Р О О; Р О Р; Р Р О; Р Р Р.

Тогда вероятность выпадения одного из этих сочетаний составит 1/8 = 0,125.

Правило № 4. Если А и В – два несовместных события, то вероятность того, что произойдет одно из них, равна сумме вероятностей появления каждого из этих событий:

Р(А или В) = Р(А) + Р(В).

Пример. Опыт с монетой. Появление орла (событие А) и решки (событие В) являются двумя несовместными событиями. Найти вероятность того, что произойдет одно из этих событий.

Решение. Вероятность события А составляет Р(А) = 0,5. Вероятность события В составляет Р(В) = 1 – Р(А) = 0,5. Тогда Р(А или В) = 0,5 + 0,5 = 1.

Пример. Бросили шестигранный кубик. Определить вероятность выпадения цифры 1 или цифры 2.

Решение. Выпадение цифры 1 (событие А) и выпадение цифры 2 (событие В) представляют собой равновероятные несовместные события: Р(А) = Р(В) = 1/6. Тогда вероятность Р(А или В) = Р(А) + Р(В) = 1/6 + 1/6 = 1/3.

Правило № 5. Вероятность появления любого одного события А1 или А2 или А3 или … Аn из N несовместных событий равна сумма вероятностей этих событий:

Р(А1 или А2 или А3 или … Аn) =

5

Пример. Опыт с кубиком. Бросили кубик. Определить вероятность появления любой цифры от 1 до 5.

Решение. Выпадение любой цифры от 1 до 5 (событие Аi) представляет собой равновероятное несовместное событие, т. е. Р(Аi) = 1/6. Тогда вероятность появления любой цифры от 1 до 5 определится как

Р(А1 или А2 или А3 или А4 или А5) = 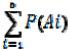= 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6.

Правило № 6. Если А и В – два независимых события, то вероятность того, что одно из этих событий произойдет, определяется как

Р(А или В) = Р(А) + Р(В) – Р(АВ) = Р(А) + Р(В) – Р(А) · Р(В).

Пример. Бросаем 2 монеты. Определить вероятность того, что на одной из двух монет выпадет орел.

Решение. Событие А выпадение орла на первой монете имеет вероятность Р(А) = 0,5. Событие В выпадения орла на второй монете имеет вероятность Р(В) = 0,5. Тогда вероятность того, что орел выпадет на одной из двух монет, составит:

Р(А или В) = Р(А) + Р(В) – Р(АВ) = Р(А) + Р(В) – Р(А) · Р(В) = 0,5 + 0,5 – 0,5 · 0,5 = 0,75.

Правило № 7. Если А и В два независимых события, то условная вероятность Р(В/А) появления события В при появлении события А определяется как

Р(В/А) = Р(АВ) / Р(А).

Пример. При изготовлении транзисторных усилителей используются транзисторы, поступающие от поставщика № 1 и поставщика № 2. 75 % транзисторов поступает от поставщика № 1 и 25 % транзисторов поступает от поставщика № 2. 99 % транзисторов поставщика № 1 исправны. 90 % транзисторов от поставщика № 2 исправны.

Определить:

1.Какова вероятность того, что любой случайно взятый транзистор окажется исправным транзистором от поставщика № 1?

2.Какова вероятность того, что любой случайно взятый транзистор окажется неисправным транзистором от поставщика № 1?

3.Какова вероятность того, что любой случайно взятый транзистор окажется исправным транзистором от поставщика № 2?

4.Какова вероятность того, что любой случайно взятый транзистор окажется неисправным транзистором от поставщика № 2?

5.Какова вероятность того, что любой случайно взятый транзистор окажется исправным независимо от его поставщика?

6

6. Какова вероятность того, что любой случайно взятый транзистор окажется неисправным независимо от его поставщика?

Решение. Событие «транзистор от поставщика № 1» обозначим как А1 , а событие «транзистор от поставщика № 2» обозначим как А2. Событие «исправный транзистор» обозначим как В1, а событие «неисправный транзистор» обозначим как В2.

Тогда:

-событие «исправный транзистор от поставщика №1» запишется как В1А1;

-событие «неисправный транзистор от поставщика №1» запишется как В2А1;

-событие «исправный транзистор от поставщика №2» запишется как В1А2;

-событие «неисправный транзистор от поставщика №2» запишется как В2А2;

-событие «исправный транзистор независимо от поставщика» запишется как В1;

-событие «неисправный транзистор независимо от поставщика» запишется как В2. Определим вероятности первых четырех событий.

Р(В1А1) = Р(В1) · (А1) = 0,99 · 0,75 = 0,7425.

Любой взятый транзистор окажется исправным транзистором от поставщика № 1 с вероятностью 0,7425.

Р(В2А1) = Р(В2) · (А1) = 0,01 · 0,75 = 0,0075.

Любой взятый транзистор окажется неисправным транзистором от поставщика № 1 с вероятностью 0,0075.

Р(В1А2) = Р(В1) · (А2) = 0,9 · 0,25 = 0,225.

Любой взятый транзистор окажется исправным транзистором от поставщика № 2 с вероятностью 0,225.

Р(В2А2) = Р(В2) · (А2) = 0,1· 0,25 = 0,025.

Любой взятый транзистор окажется неисправным транзистором от поставщика № 2 с вероятностью 0,025.

Проверка. Все перечисленные выше события составляют полную группу событий, т. к. других событий быть не может. Вероятность полной группы событий равна единице, следовательно, должно выполняться условие:

Р(В1А1) + Р(В2А1) + Р(В1А2) + Р(В2А2) = 1.

Проверим выполнение этого условия в нашем случае:

Р(В1А1) + Р(В2А1) + Р(В1А2) + Р(В2А2) = 0,7425 + 0,0075 + 0,225 + 0,025 = 1.

Условие соблюдается, поэтому вероятность всех событий была определена правильно.

Определим вероятности последних двух событий.

Р(В1) = Р(В1А1) + Р(В1А2) = 0,7425 + 0,225 = 0,9675.

Любой взятый транзистор окажется исправным независимо от поставщика с вероятностью 0,9675.

Р(В2) = Р(В2А1) + Р(В2А2) = 0,0075 + 0,025 = 0,0325.

Любой взятый транзистор окажется неисправным независимо от поставщика с вероятностью 0,0325.

7

Проверка. Все перечисленные выше события составляют полную группу событий, т. к. других событий быть не может. Вероятность полной группы событий равна единице, следовательно, должно выполняться условие:

Р(В1) + Р(В2) = 1.

Проверим выполнение этого условия в нашем случае:

Р(В1) + Р(В2) = 0,9675 + 0,0325 = 1.

Условие соблюдается, поэтому вероятность всех событий была определена правильно.

Правила теории вероятности широко используются в технической диагностике при оценке состояния объекта по косвенным признакам.

ЛИТЕРАТУРА

1. Надежность и диагностика систем электроснабжения железных дорог : учебник для вузов ж.-д. транспорта / А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000. –

С. 398–401.

ПРАКТИЧЕСКАЯ РАБОТА № 2

Применение метода Байеса для косвенной диагностики состояния объектов (2 часа)

Цель работы: изучить статистический метод распознавания технического состояния объекта, основанный на обобщенной теореме Байеса.

ПРИМЕНЕНИЕ МЕТОДА БАЙЕСА ДЛЯ КОСВЕННОЙ ДИАГНОСТИКИ СОСТОЯНИЯ ОБЪЕКТОВ

Метод Байеса является одним из наиболее простых и точных методов косвенной диагностики состояния объекта по априорным статистическим данным. Априорными называются данные о состоянии объектов, полученные опытным (экспериментальным путем). Такие данные накапливаются со временем и являются достаточно точными, если получены в результате наблюдений за большим количеством однотипных объектов в течение длительного времени.

Допустим, что объект имеет какое-то состояние, называемое диагнозом Di. В этом состоянии объект может иметь, а может и не иметь некоторый признак Кj. В свою очередь, признак Кj может проявляться у объекта с диагнозом Di, а может проявляться и у объектов с другими диагнозами. События наличия у объекта диагноза Di и признака Кj являются совместными событиями и могут появляться одновременно. Появление диагноза Di является случайным событием, но имеются статистические данные о том, что при его наличии у определенного числа объектов имеется признак Кj. Эти

8

статистические данные позволяют определить вероятность Р(DiКj) совместного появления у объекта диагноза Di и признака Кj.

Вероятность появления двух совместных событий связана с условной вероятностью появления одного из событий при наличии другого следующим образом:

Р(DiКj) = Р(Di)· Р(Кj/Di) = Р(Кj)· Р(Di/Кj).

Теорема Байеса вытекает из этого равенства и записывается в виде:

Р(Di/Кj) = Р(Di)· Р(Кj/Di) / Р(Кj),

где Р(Di/Кj) – условная вероятность появления диагноза Di у объекта с признаком Кj; Р(Di) – априорная вероятность диагноза Di у любого объекта, определенная по статистическим данным; Р(Кj/Di) – априорная условная вероятность появления признака Кj у объекта с диагнозом Di; Р(Кj) – априорная вероятность появления признака Кj у любого объекта.

Пример. Проведены измерения переходных сопротивлений 1000 питающих зажимов. 990 зажимов имеют сопротивление в пределах ТУ. 10 зажимов имеют сопротивление выше норм ТУ и признаны неисправными. Неисправность будем считать диагнозом Di. Все зажимы были проверены также термографическим методом на предмет нагрева. 28 зажимов имели повышенную температуру. Повышенную температуру зажима будем считать признаком Кj. Из 10 неисправных зажимов 8 имели повышенную температуру, т. е. 8 объектов с признаком Кj имели диагноз Di. Определить условную априорную вероятность наличия признака Кj у объектов с диагнозом Di.

Определить априорную вероятность неисправности питающих зажимов, т. е. наличия диагноза Di.

Решение. Число обследованных зажимов N* = 1000. Число исправных зажимов N = 990. Число неисправных зажимов Ni = 10. Диагноз Di «неисправен» имеет 10 зажимов. Тогда априорная вероятность неисправности зажимов и, следовательно, наличия диагноза Di составит:

Р(Di) = Ni/N* = 10/1000 = 0,01.

Определить априорную вероятность наличия у зажимов повышенной температуры, т.е. наличия признака Кj.

Решение. Число обследованных зажимов N* = 1000. Число зажимов с повышенной температурой Nj = 28. Тогда априорная вероятность повышенной температуры зажимов и, следовательно, наличия признака Кj составит:

Р(Кj) = Nj /N* = 28/1000 = 0,028.

9

Определить условную априорную вероятность наличия повышенной температуры у неисправных зажимов

Решение. Число неисправных зажимов с диагнозом Di составит: Ni = 10. Число неисправных зажимов с повышенной температурой, т. е. с признаком Кj, Nij = 8. Тогда условная априорная вероятность наличия повышенной температуры у неисправных зажимов составит:

Р(Кj/Di) = Nij / Ni = 8 / 10 = 0,8.

Определить условную вероятность неисправности зажима при его повышенной температуре.

Решение. Условная вероятность неисправности зажима (диагноз Di) при повышенной температуре (признак Кj) определится как

Р(Di/Кj) = Р(Di)· Р(Кj/Di) / Р(Кj) = 0,01· 0,8/ 0,028 = 0,286.

Таким образом, состояние объекта может быть определено по косвенным признакам. Однако полученный в данном случае результат свидетельствует о невысокой достоверности такой диагностики. Достоверность косвенного диагностирования может быть значительно повышена путем увеличения числа обследованных типовых объектов и путем увеличения числа косвенных признаков, свидетельствующих об их неисправности.

Если каждое из n состояний объекта характеризуется комплексом признаков К1 , К2, … КL ϵ К*, то применяется обобщенная формула Байеса:

Р( Di/К*) = [Р( Di) · Р(К*/Di)]/ Р(К*),

где Р( Di/К*) – условная вероятность нахождения объекта в диагнозе Di при условии, что в ходе обследования была получена реализация К* комплекса признаков Кj; Р(К*) – вероятность появления конкретной реализации К* комплекса признаков Кj у всех диагностируемых объектов, независимо от их технического состояния; Р(К*/Di) – условная вероятность появления конкретной реализации К* комплекса диагностических признаков Кj для объекта, находящегося в диагнозе Di.

Поскольку объект может находиться только в одном из n возможных технических

Кроме того, считается, что отдельные диагностические признаки К1 , К2, … КL из множества К* являются независимыми. Тогда из правила вероятности совместного появления независимых событий следует, что:

10