4.9. Звенья с модулированным сигналом

До сих пор рассматривались звенья, в которых сигнал был немодули­рованным. В автоматических системах часто используются звенья (чувстви­тельные элементы, усилители, серводвигатели и т. п.), у которых сигнал представляет собой переменное напряжение (или ток) некоторой частоты ω₀, называемой несущей. В этом случае закон изменения сигнала во времени характеризуется измене­нием амплитуды или действующего значе­ния этого напряжения, т. е. огибающей. На рис. 2.27 для иллюстрации приведены формы немодулированного и модулирован­ного сигналов. Изменению знака сигнала соответствует изменение фазы несущей часто­ты ω₀ на 180º.

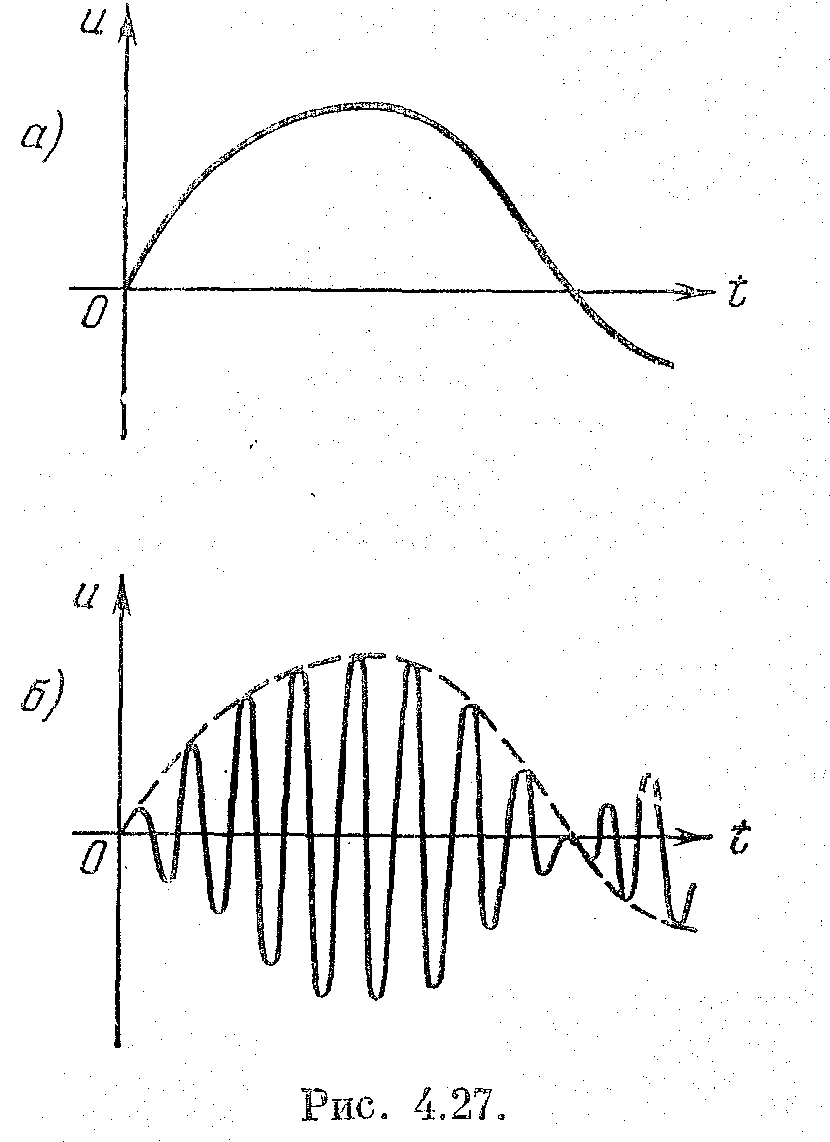
Рис. 2.27

При расчете автоматических систем с модулированным сигналом могут возникать две задачи:

1) нахождение такого звена, которое по своему воздействию на огибающую модули­рованного сигнала было бы эквивалентным какому-либо обычном звену, используемому в системах с немодулированным сигналом, например апериодическому первого поряд­ка, дифференцирующему, интегрирующему и т. п.;

2) определение воздействия звена с заданной передаточной функцией на огибающую модулированного сигнала, т. е, нахождение передаточной функции по огибающей.

Рассмотрим первую задачу. Ниже без строгих доказательств показы­вается путь, позволяющий сформулировать требования к частотной переда­точной функции звена, чтобы его воздействие на огибающую сигнала было определенным и заранее заданным.

Для уяснения этого пути обратимся к какому-либо простейшему звену с немодулированным сигналом, например к апериодическому звену первого порядка. Для определенности в качестве такого звена возьмем RC-цепь (рис. 2.13, д). Передаточная функция этого звена

где

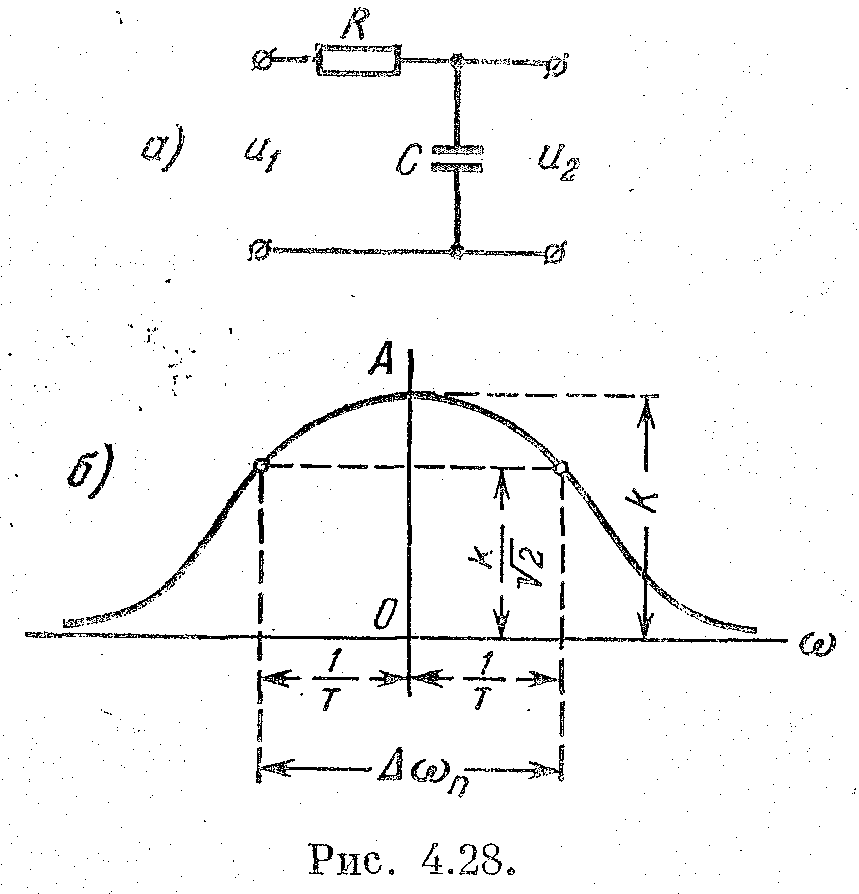
Рис. 2.28

Представим себе, что динамические свойства рассматриваемого звена изучаются при помощи экспериментального снятия его амплитудной частот­ной характеристики. Для этой цели на вход RC-цепи нужно подавать напря­жение от источника с переменной частотой, например от звукового генера­тора, и измерять отношение амплитуд выходного и входного напряжений. Характеристика снимается только для положительных частот, а затем дополняется симметричной ветвью в области отрицательных частот (рис. 2.28).

По отношению к амплитудной частотной характеристике можно при­менить следующий формальный прием. Входное напряжение при снятии частотной характеристики представляет собой гармоническую функцию с угловой частотой ω и амплитудой

(2.65)

Используя понятие отрицательной частоты, можно представить эту функцию в виде алгебраической суммы сигнала положительной частоты и сигнала отрица­тельной частоты:

(2.66)

Эти сигналы называются боковыми частотами. Название произошло по сле­дующей причине. Если на вход звена поступает постоянны по величине сигнал, то его можно представить как сигнал нулевой частоты. В этом случае коэффициент передачи звена равен орди­нате пересечения амплитудной характеристикой оси ординат. В рассматри­ваемой RC-цепи этот коэффициент равен единице, т.е. k = 1.

Если теперь на вход звена подать сигнал, представляющий собой гармо­ническую функцию, то реакцию звена на такой сигнал можно получить, рассматривая реакцию звена на две частоты, расположенные симметрично относительно исходной нулевой частоты. Эти две частоты и являются боко­выми по отношению к исходной частоте.

При наличии амплитудной частотной характеристики (рис. 2.28) посто­янная времени звена может быть определена по эффекту подавления, боко­вых частот по сравнению с исходной нулевой частотой. Из выражения для амплитудной частотной характеристики апериодического звена первого порядка (см. табл. 2.3) в общем случае, когда k ≠ 1,

следует, что на нулевой частоте коэффициент передачи звена по амплитуде равен k, а при этот коэффициент равен

На основании этого соотношения по амплитудной характеристике можно легко найти постоянную времени. Для этой цели на высоте 0,707k проводится горизонтальная линия до пересечения с амплитудной характеристикой. Абсциссы точек пересечения будут равны в области положительных частот ив области отрицательных частот.

Расстояние между точками пересечения часто называют полосой про­пускания звена (2.25):

Постоянная времени может быть вычислена по полосе пропускания:

(2.67)

Обратимся теперь к звену с модулированным сигналом. Предположим, что динамические свойства некоторого звена изучаются при помощи частот­ных характеристик (рис. 2.29). Постоянному сигналу на входе такого звена соответствует напряжение

(2.68)

где ω₀ – несущая угловая частота.

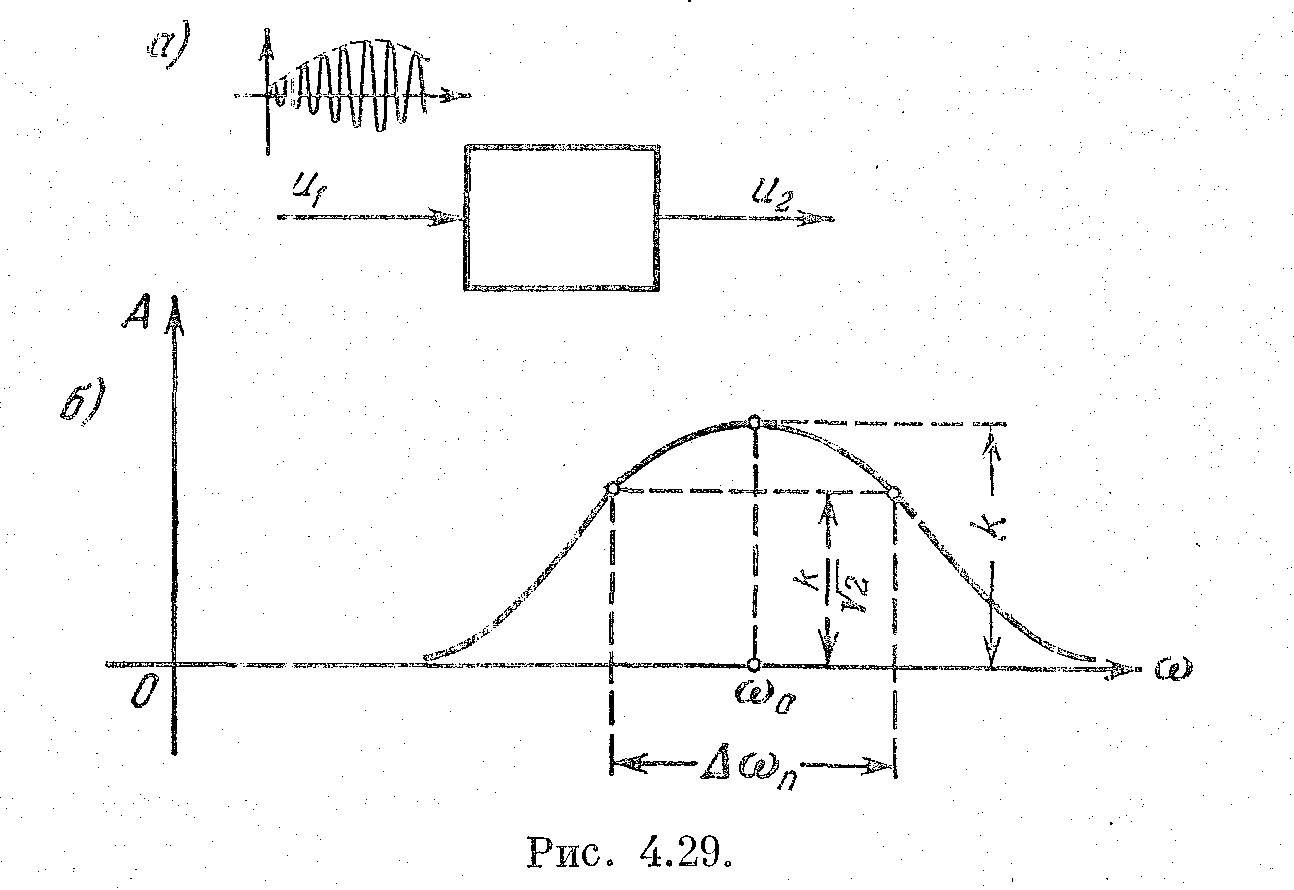
Рис. 2.29

Допустим теперь, что сигнал (огибающая) изменяется по гармониче­скому закону с угловой частотой О. Это значит, что по гармоническому закону должна изменяться амплитуда в выражении (2.68), и модулированный сигнал может быть представлен в виде

(2.69)

где гармонический закон изменения огибающей (сигнала).

Это выражение может быть преобразовано к виду

(2.70)

Таким образом, модулированный сигнал (2.69) может быть заменен двумя гармоническими сигналами с частотами, равными сумме и разности несущей частоты и частоты огибающей: и. Эти гармонические сигналы являются боковыми частотами.

Выясним теперь, какой должна быть амплитудная частотная характе­ристика звена, чтобы по отношению к модулированному сигналу звено представляло собой, например, апериодическое звено первого порядка. Очевидно, что характеристика должна быть такой же самой, как характери­стика апериодического звена с немодулированным сигналом, но она должна быть симметричной относительно несущей частоты ω₀ (рис. 2.29). Тогда боковые частоты будут подавляться рассматриваемым звеном так же, как они подавляются звеном с немодулированным сигналом (рис. 2.28).

Постоянную времени звена с модулированным сигналом, если оно пред­ставляет собой для огибающей апериодическое звено первого порядка, можно определить по той частоте огибающей, при которой боковые частоты подавляются в раз.

Для этого, аналогично предыдущему, на амплитудной частотной харак­теристике звена (рис. 2.29) должно быть сделано следующее построение. Необходимо определить коэффициент передачи звена k на несущей частоте, что соответствует постоянному входному сигналу (2.68) или частоте огибаю­щей Ω=0. Затем на высоте 0,707k проводится горизонтальная прямая до пересечения с частотной характеристикой и определяется полоса про­пускания Δω_П. Постоянная времени определяется на основании (2.67) и равна

Рассмотренная выше методика позволяет сформулировать правило, уста­навливающее требования к амплитудной частотной характеристике звена с модулированным сигналом для того, чтобы его воздействие на огибающую было таким же, каким является воздействие обычного звена заданного типа на немодулированный сигнал. Это правило сводится к следующему. Ампли­тудная частотная характеристика звена с модулированным сигналом должна быть такой же, как амплитудная частотная характеристика звена с немоду­лированным сигналом, но эта характеристика должна быть симметричной не относительно оси ординат, а относительно несущей частоты. Звено с немодулированным сигналом может рассматриваться: при этом как частный слу­чай звена с модулированным сигналом при несущей частоте ω₀ = 0.

Для того чтобы избежать ошибок в связи с наличием неминимально-фазовых звеньев, сформулированное выше правило для амплитудных харак­теристик должно быть дополнено аналогичным правилом для фазовых частотных характеристик. Если известно, что все рассматриваемые звенья относятся к категории минимально-фазовых звеньев, то привлечение фазовых характеристик не является необходимым и можно ограничиться использо­ванием только амплитудных характеристик.

Таким образом, в общем случае, если обозначить эквивалентную частот­ную передаточную функцию по огибающей, то для частотной пере­даточной функции звена с модулированным сигналом W (jΩ) должно выпол­няться условие

(2.71)

Так, например, если необходимо, чтобы по своему действию на огибаю­щую модулированного сигнала звено соответствовало апериодическому звену первого порядка с эквивалентной частотной передаточной функцией

то оно должно иметь частотную передаточную функцию

Приблизительно такую передаточную функцию имеют, в частности, резонансные усилители, настроенные на несущую частоту ω₀, причем постоян­ная времени: Т определяется полосой пропускания усилителя в соответствии с (2.67).

Проиллюстрируем применение изложенного правила на другом примере, Возьмем рассмотренную ранее дифференцирующую RС -цепь (рис. 2.24, а). Эта цепь годится для дифференцирования немодулированного сигнала. Если на ее вход подать модулированный сигнал, то дифференцирования не полу­чится. Действительно, рассмотрим входной сигнал и₁, где представляет собой закон изменения амплитуды во времени, т. е. оги­бающую или сам передаваемый сигнал. Продифференцируем это выражение, считая для простоты, что дифференцирующая цепь идеальна:

(2.72)

В результате получилось два слагаемых. Первое слагаемое является полезным, так как содержит требуемую производную от огибающей, а вто­рое – вредным, так как оно представляет собой ложный сигнал, который может в сотни и тысячи раз превышать по уровню полезный сигнал.

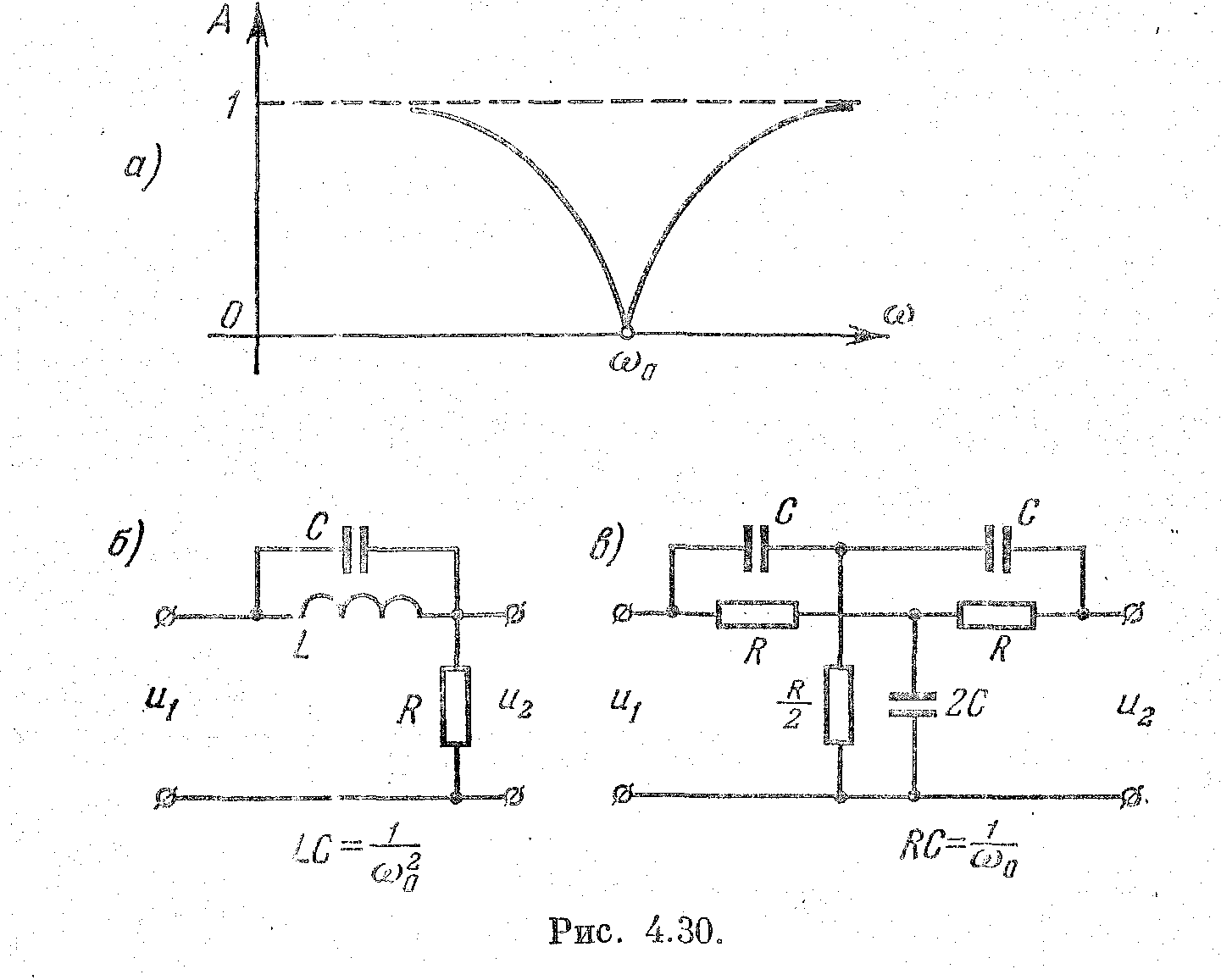
Рис. 2.30

Амплитудная частотная характеристика дифференцирующей RС-цепи (дифференцирующего звена с замедлением) изображена в табл. 2.7. Для получения дифференцирования огибающей модулированного сигнала необходимо осуществить такую цепь, у которой амплитудная характеристика была бы подобна изображенной в табл. 2.7 и была бы при этом расположена сим­метрично относительно несущей частоты. Такая характеристика изображена на рис. 2.30, а.

Из рассмотрения характеристики следует, что звено не должно про­пускать несущую частоту. Это должно быть понятным и физически, так как несущая частота в чистом виде, т. е. отсутствие боковых частот, будет при постоянном сигнале на входе (см. (2.68)). В этом случае производная сигнала (по огибающей) будет равна нулю и на выходе звена не должно быть никакого сигнала.

При изменении сигнала по какому-либо закону, например в соответствии с выражением (2.69), появятся боковые частоты, которые будут пропу­скаться звеном тем сильнее, чем дальше они отстоят от несущей частоты, т. е. чем больше частота огибающей. Таким образом, звено будет обладать дифференцирующими свойствами по отношению к огибающей модулирован­ного сигнала.

Амплитудная частотная характеристика, изображенная на рис. 2.30, а, может реализоваться различным образом. Такая характеристика может быть получена, например, от резонансной параллельной LС-цепи, Т-образной цепи и т. п., настроенных на несущую частоту (рис. 4.30, б и в).

Обратимся теперь ко второй указанной выше задаче. При известной частотной передаточной функции звена W (jω) определим эквивалентную частотную передаточную функцию W_Э (jΩ) для огибающей модулированного сигнала. Для этого вспомним, что частотная передаточная функция звена (2.17)

представляет собой комплексное число, модуль которого А (ω) равен отно­шению амплитуд выходной и входной величии, а аргумент ψ – сдвигу фаз при гармоническом входном сигнале в установившемся режиме. Если на входе звена действует величина , то на выходе будет

(2.73)

Для получения частотной передаточной функции по огибающей W_Э (jΩ) звена с модулированным сигналом обратимся к гармоническому сигналу по огибающей (2.69). Разложим его на боковые частоты ω₀ +Ω и и ω₀–Ω , в соответствии с выражением (2.70). Тогда, используя зависимость (2.73), получим

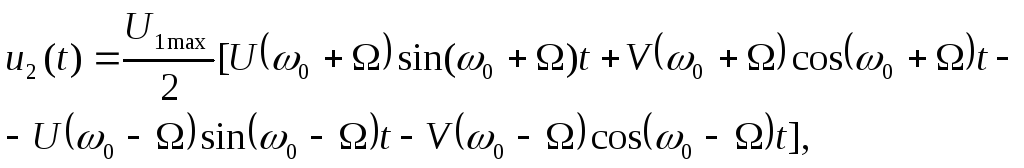(2.74)

где U(ω) и V(ω) – вещественная и мнимая части частотной передаточной функции W(jω).

Путем разложения синусов и косинусов сумм и разностей углов это выражение преобразуется к виду

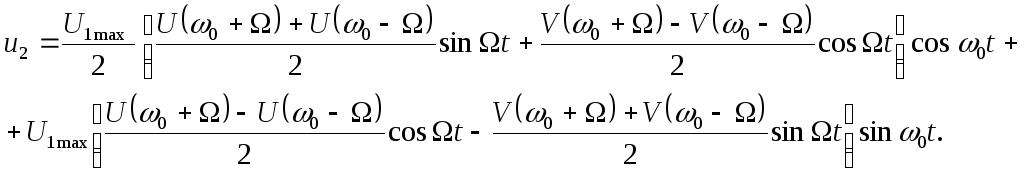(2.75)

Остановимся теперь на двух важных частных случаях.

1. Рассмотрим случай «симметричной» относительно несущей частоты частотной передаточной функции, что определяется равенством , где звездочкой отмечена сопряженная комплекс­ная величина. Из этого равенства вытекают два других:и.

Тогда формула (2.75) существенно упрощается и может быть записана в виде

(2.76)

Рассматривая огибающую, т. е. отбрасывая множитель cos ω₀t, и сравни­вая выражения (2.76) и (2.73), убеждаемся, что эквивалентная частотная передаточная функция для огибающей W_Э (jω) может быть получена из частотной передаточной функции звена W (jω) подстановкой ω = ω₀ + Ω:

(2.77)

что согласуется с полученной ранее формулой (2.71).

Так, например, если звено типа резонансного усилителя имеет частотную передаточную функцию

то передаточная функция для огибающей будет

Переход к обычной передаточной функции может быть сделан заменой jΩ=р. В результате из (2.77) получаем

(2.78)

2. Рассмотрим теперь другой важный случай, когда передаточная функ­ция W (jω) не является «симметричной», но слагаемое в формуле (2.75), определяемое множителем sin ω₀t, отсеивается в последующих звеньях каким-либо фазочувствительным устройством, например фазовым дискрими­натором. Тогда это слагаемое может быть отброшено и формула (2.74) упро­щается:

(2.79)

Так как U (ω) – функция четная, а V (ω) – нечетная, то последнее выражение может быть представлено в следующем виде:

(2.80)

В этом случае эквивалентная частотная передаточная функция для огибающей может быть определена из выражения

(2.81)

Аналогичный результат может быть получен, если фазочувствительное устройство пропускает сигнал фиксированной фазы, например , где φ =const. Тогда вместо выражения (2.81) полу­чается

(2.82)

Переход к обычной передаточной функции W_э(p) делается, как и выше, заменой jΩ = р.

Формулы (2.81) и (2.82) позволяют просто находить передаточную функцию по огибающей. Однако к ним следует относиться с осторожностью. Сформулированное выше условие применимости этих формул заключалось в том, что можно было отбросить слагаемое в (2.75), пропорциональное sin ω₀t, и оставить слагаемое, пропорциональное cos ω₀t или в общем случае cos (ω₀t +φ). Однако для этого еще недостаточно, чтобы последующее фазочувствительное устройство в принципе могло отсеивать слагаемое с множителем sin ω₀t. Необходимо, чтобы это можно было реализовать, технически, для чего нужна относительная малость слагаемого с sin ω₀t по сравнению со слагаемым с cos ω₀t. Только в этих условиях при имеющейся, всегда нестабильности фазочувствительного устройства может быть уверенно выделено слагаемое с множителем cos ω₀t.

Таблица 4.8

Эквивалентные передаточные функции для огибающей некоторых звеньев

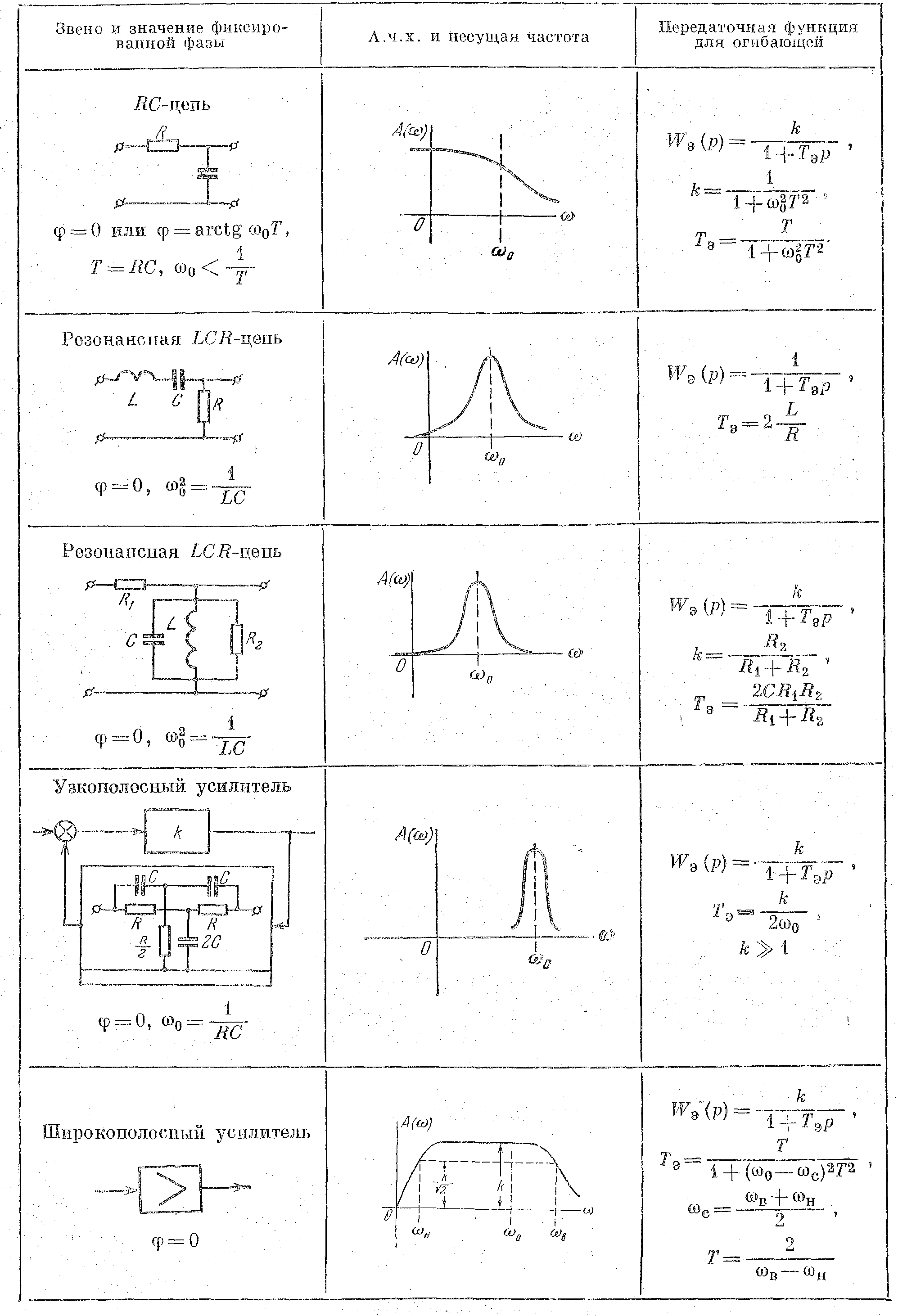
В качестве примера, иллюстрирующего случай, когда формула (2.81) практически неприменима, рассмотрим опять дифференцирующую RC-цепь (рже. 2.24, а). Примем для простоты, что ее частотная передаточная функция соответствует идеальному дифференцирующему звену W (jω) = kjω. Тоща, в соответствии с формулой (2.81), частотная передаточная функция для огибающей будет

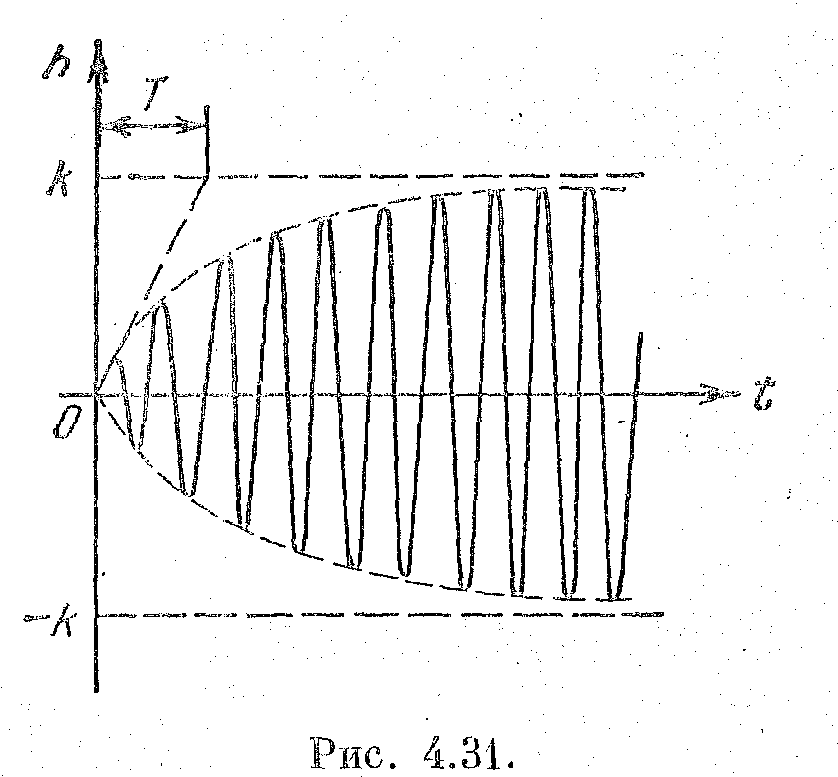
Рис. 2.31

Это выражение показывает, что звено обладает дифференцирующими свойствами и для огибающей. Действительно, если обратиться к формуле (2.72), то видно, что при устранении слагаемого с множителем sin ω₀t звено будет обладать дифференцирующими свой­ствами. Однако, как уже указывалось выше при анализе выражения (2.72), его второе (вредное) слагаемое может в сотни и тысячи, раз превышать первое (полезное) слагаемое. Выделить первое слагаемое и отсеять второе практически не удается. Поэтому обычная дифференцирующая RC-цепь не может применяться, для диф­ференцирования огибающей.

Пользоваться формулами (2.81) и (2.82) можно тем уверенней, чем большую симметрию относительно несущей частоты будет иметь частотная передаточная функ­ция звена W (jω). При полной симметрии слагаемое с множителем sin ω₀t в выражении (2.75) будет отсутствовать и формула (2.81) вырождается в формулу (2.77). В рассмотренном примере дифференцирующей RC-цепь частотная передаточная функция обладает сильной несимметрией относительно несу­щей частоты, что и привело к отрицательному результату.

В табл. 2.8 приведены приближенные значения передаточных функции для некоторых звеньев с модулированным сигналом, используемых в прак­тике и сводящихся для огибающей к апериодическому звену первого порядка. Параметры передаточных функций определены для фиксированной фазы последующего фазочувствителъного устройства φ = const. Эта фаза может устанавливаться равной нулю (φ = 0), т. е. устройство фазируется с вход­ным сигналом звена (2.69). Фазочувствителыное устройство может фазиро­ваться также с выходным сигналом звена при постоянном, входном сигнале вида (2.68). В этом случае φ = φ₀ = const, где φ₀ – фазовый сдвиг несущей частоты при входном сигнале . При симметричной отно­сительно несущей частоты частотной передаточной функции соблюдается условие φ = φ₀ = const.

На рис. 2.31 изображена для иллюстрации переходная характеристика звена с модулированным сигналом, эквивалентная для огибающей аперио­дическому звену первого порядка.