
- •2 Характеристики типовых звеньев систем автоматического регулирования и управления
- •2.1 Общие понятия
- •2.2 Временные характеристики
- •4.3 Частотная передаточная функция и частотные характеристики
- •4.4. Логарифмические частотные характеристики
- •4.5 Позиционные звенья
- •4.6 Интегрирующие звенья
- •4.7 Дифференцирующие звенья
- •4.8. Неустойчивые и неминимально-фазовые звенья
- •4.9. Звенья с модулированным сигналом
4.3 Частотная передаточная функция и частотные характеристики
Важнейшей
характеристикой динамического звена
является его частотная
передаточная функция. Для
получения ее рассмотрим динамическое
звено (рис. 2.1) в случае, когда возмущение
![]() ,
а на входе имеется гармоническое
воздействие
,
а на входе имеется гармоническое
воздействие![]() ,
где
,
где
![]() амплитуда,
а
амплитуда,
а![]() угловая
частота этого воздействия.
угловая
частота этого воздействия.
На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая: по фазе относительно входной величины на угол ψ. Таким образом, для выходной величины можно записать
![]()
Воспользуемся формулой Эйлера и представим входную и выходную величины в виде суммы экспоненциальных функций:
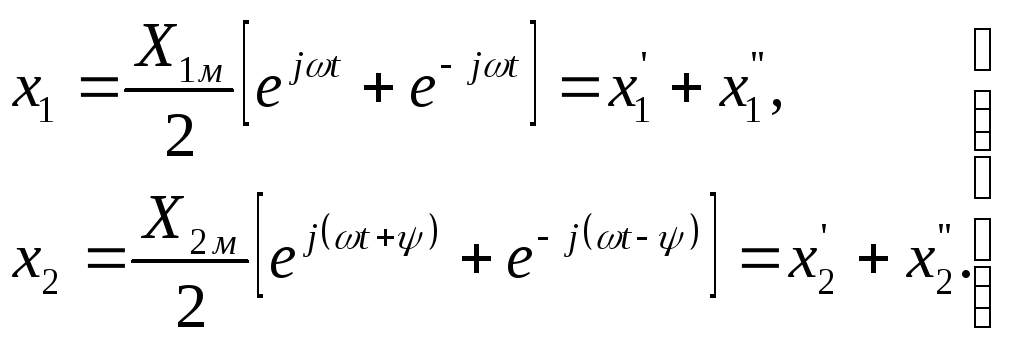 (2.10)
(2.10)
В
линейной системе на основании принципа
суперпозиции можно рассмотреть
отдельно прохождение составляющих
![]() и
и
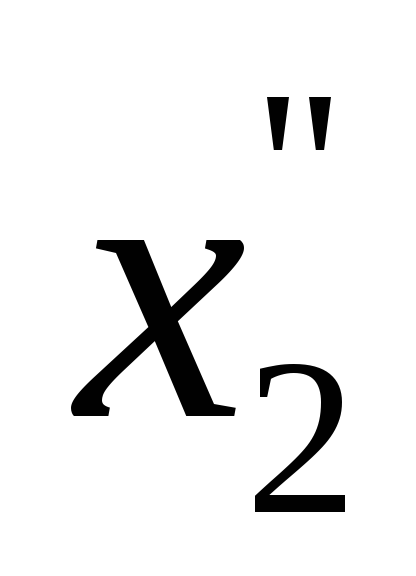 .
Кроме
того, можно легко показать, что достаточно
рассмотреть прохождение только
составляющей
.
Кроме
того, можно легко показать, что достаточно
рассмотреть прохождение только
составляющей![]() ,
которая
в выходной величине дает составляющую
,
которая
в выходной величине дает составляющую![]() .
Соотношение
между составляющими
.
Соотношение
между составляющими
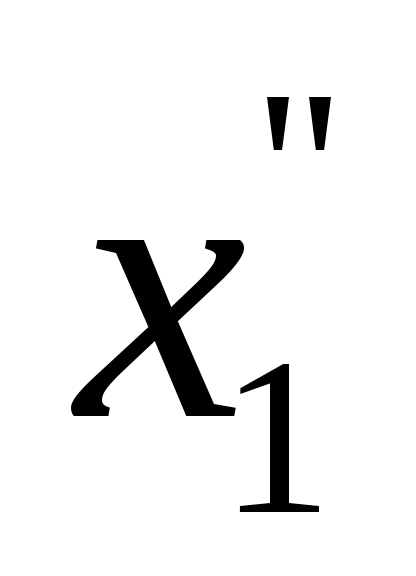 и
и
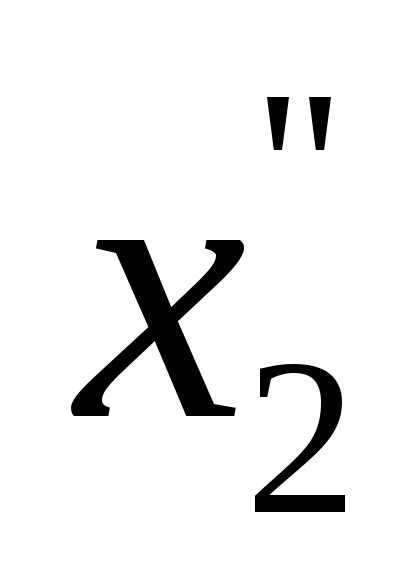 получается
таким же, как между
получается
таким же, как между
![]() и
и
![]() .
Поэтому
в дальнейшем рассмотрении воспользуемся
символической записью
.
Поэтому
в дальнейшем рассмотрении воспользуемся
символической записью
![]() .
Тогда
.
Тогда
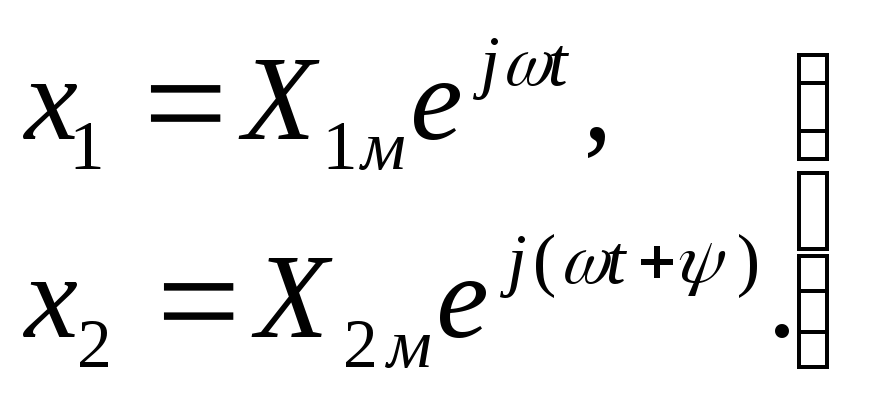 (2.11)
(2.11)
Символичность
этой сокращенной записи заключается в
отбрасывании составляющих с множителем
![]() .
.
Для нахождения соотношения между входной и выходной гармоническими величинами звена воспользуемся его дифференциальным уравнением в виде
![]()
Из выражений (2.11) определим производные:

Подставив значения входной и выходной величин и их производных
в исходное дифференциальное уравнение, получим:
![]()
откуда
после сокращения на общий множитель
![]() найдем:
найдем:
![]() (2.12)
(2.12)
Это
выражение называется частотной
передаточной функцией звена.
Таким образом, частотная передаточная
функция
![]() представляет собой комплексное число,
модуль которого равен отношении амплитуды
выходной
величины
к амплитуде входной, а аргумент – сдвигу
фаз выходной величины по отношению к
входной:
представляет собой комплексное число,
модуль которого равен отношении амплитуды
выходной
величины
к амплитуде входной, а аргумент – сдвигу
фаз выходной величины по отношению к
входной:
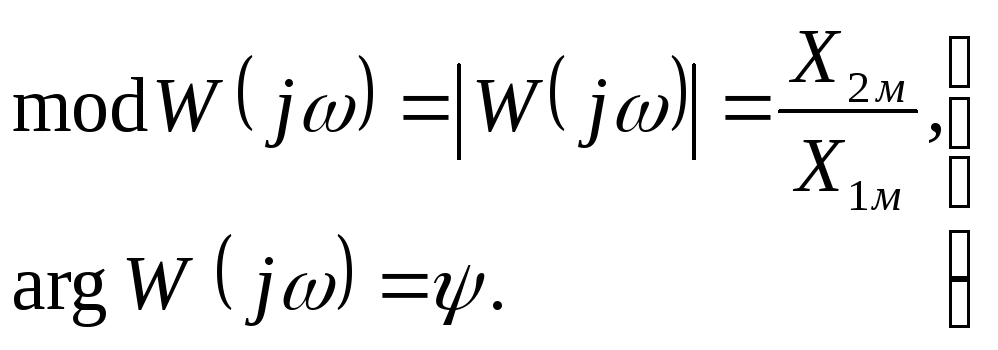 (2.13)
(2.13)
В более общей формулировке для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений Фурье (частотных изображений) выходной и входной величин:
![]() (2.14)
(2.14)
что
непосредственно вытекает из формулы
(4.1) при переходе от изображения-Лапласа
к изображению Фурье; следовательно,
частотная передаточная функция легко
получается из обычной передаточной
функции подстановкой
![]() .
.
Частотная передаточная функция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование
![]() (2.15)
(2.15)
Частотная передаточная функция может быть представлена в следующем виде:
![]() (2.16)
(2.16)
где А (ω) – модуль частотной передаточной функции, ψ (ω) – аргумент или фаза, U (ω) и V (ω) – вещественная и мнимая составляющие частотной передаточной функции.
Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Для рассмотренного выше примера (2.12)
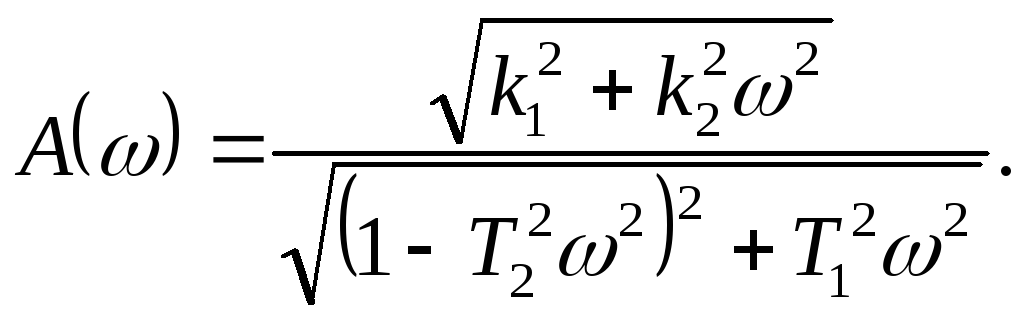
Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя. Для (2.12) имеем:
![]()
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную ж мнимую части. Для (2.12)
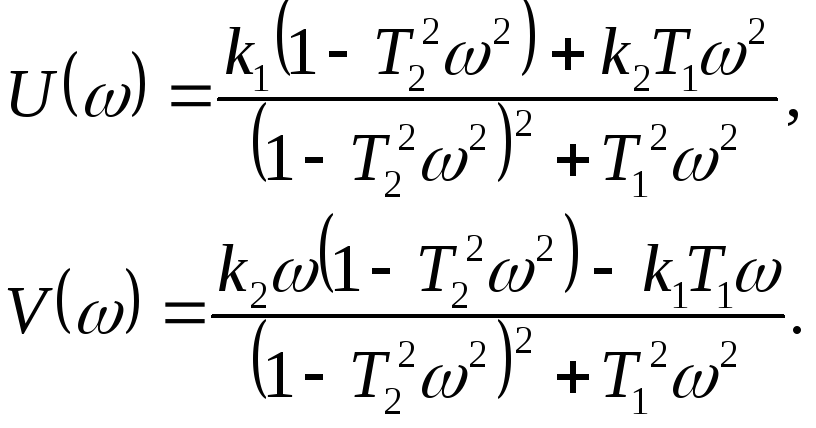
Для наглядного представления частотных свойств звена используют так называемые частотные характеристики.
и
Рис.
2.7
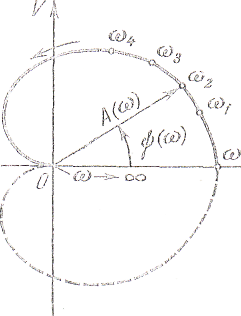
![]() при изменении частота от нудя до
бесконечности (рис. 2.7). По оси абсцисс
откладывается вещественная часть
при изменении частота от нудя до
бесконечности (рис. 2.7). По оси абсцисс
откладывается вещественная часть![]() и по оси ординат – мнимая часть
и по оси ординат – мнимая часть![]() .
Для каждой частоты на комплексной
плоскости наносится точка. Полученные
точки соединяются затем величина
плавной кривой. Около нанесенных точек
можно написать соответствующие им
частоты
.
Для каждой частоты на комплексной
плоскости наносится точка. Полученные
точки соединяются затем величина
плавной кривой. Около нанесенных точек
можно написать соответствующие им
частоты![]() и т. д.
и т. д.
А. ф. х. может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции + и получится сопряженная комплексная величина. Поэтому а.ф.х. для отрицательных частот может быть построена как зеркальное изображение относительно вещественной оси а. ф. х. для положительных частот. На рис. 2.7 а. ф. х. для отрицательных частот показана пунктирной линией.
Отметим, в чем заключается смысл положительных и отрицательных частот. При помощи преобразования Фурье
![]()
функция
времени х
(t)
преобразуется
в функцию частоты
![]() .
Это означает, что функция времени
представляется в виде бесконечной суммы
бесконечно малых по величине векторов,
вращающихся на комплексной плоскости
с различными угловыми скоростями
(частотами).
Эта сумма определяется формулой обратного
преобразования Фурье
.
Это означает, что функция времени
представляется в виде бесконечной суммы
бесконечно малых по величине векторов,
вращающихся на комплексной плоскости
с различными угловыми скоростями
(частотами).
Эта сумма определяется формулой обратного
преобразования Фурье
![]()
где с – абсцисса абсолютной сходимости.
Так
как функция времени является вещественной,
то каждому элементарному вектору
![]() ,
вращающемуся против часовой стрелки
(
>0), должен соответствовать элементарный
сопряженный вектор
,
вращающемуся против часовой стрелки
(
>0), должен соответствовать элементарный
сопряженный вектор
![]() вращающийся
по часовой стрелке (
< 0). В этом случае сумма таких векторов
в любой момент времени будет всегда
вещественной. Поэтому интегрирование
в формуле обратного преобразования
Фурье должно вестись по всем, частотам
от
до .
вращающийся
по часовой стрелке (
< 0). В этом случае сумма таких векторов
в любой момент времени будет всегда
вещественной. Поэтому интегрирование
в формуле обратного преобразования
Фурье должно вестись по всем, частотам
от
до .
Примером представления функции времени в виде суммы сопряженных векторов, вращающихся в разные стороны, может служить изображение гармонических функций по формулам Эйлера, например (2.10).
Таким образом, положительные и отрицательные частоты имеют определенный смысл, так как они соответствуют положительным и отрицательным угловым скоростям вращения, векторов на комплексной плоскости.
В принципе можно ограничиться рассмотрением только положительных частот. Однако при использовании всего диапазона частот от до многие формулы получают более удобный и симметричный вид.
Длина вектора, проведенного из начала координат в точку а. ф. х. соответствующую какой-то выбранной частоте, равна модулю частотной передаточной функции. Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции. Таким образом, а. ф. х. возможность наглядно представить для. каждой частоты входного воздействия звена отношение амплитуд выходной и входной величин и сдвиг фаз между ними.
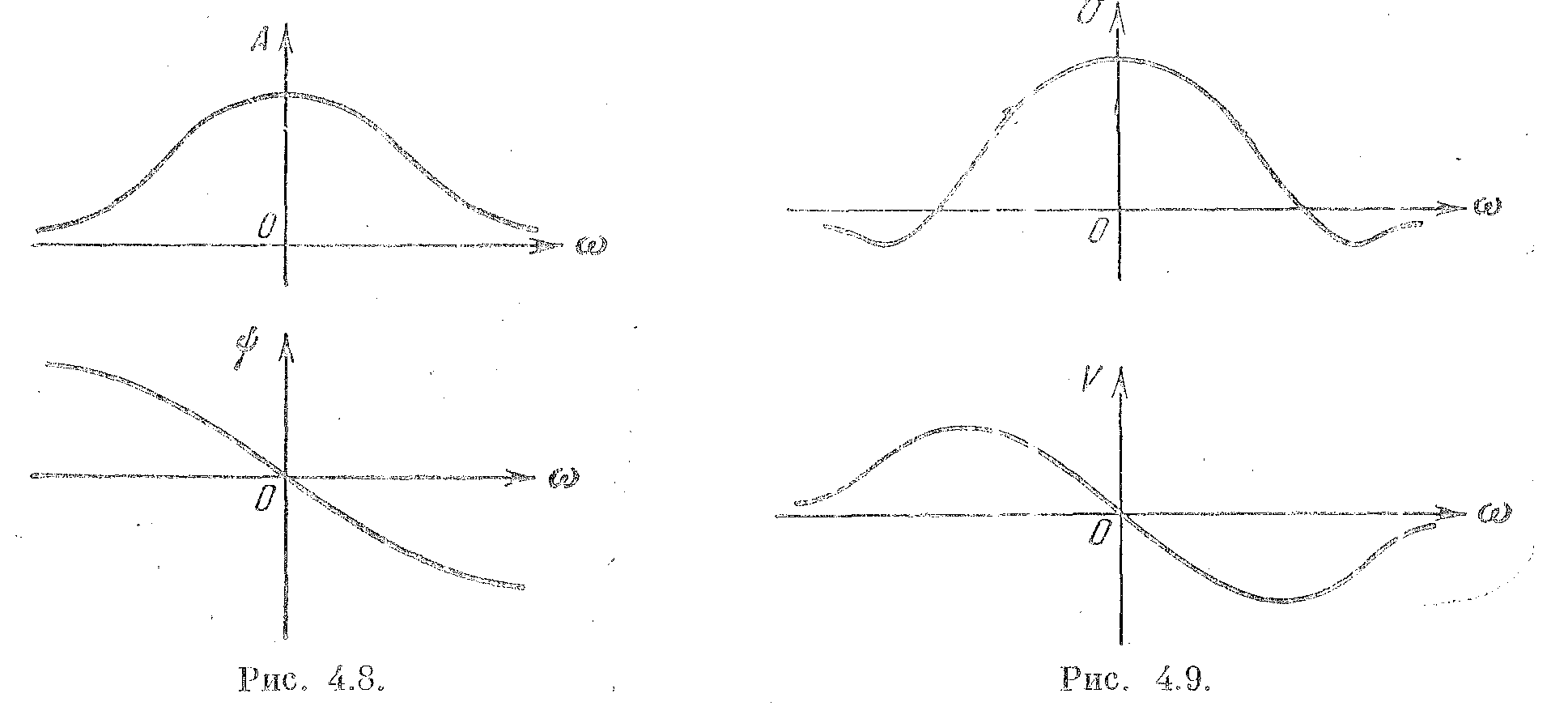
Рис. 2.8 Рис. 2.9
Построение а. ф. х. по вещественной и мнимой частям частотной передаточной функции, как правило, является трудоемкой работой, так как умножение частотной передаточной функции на комплексную величину, сопряженную ее знаменателю, повышает в два, раза степень частоты в знаменателе. Обычно гораздо проще строить а. ф. х., используя полярные координаты, т. е. вычисляя непосредственно модуль и фазу. Зная модуль и фазу, можно легко достроить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.
Вместо а. ф. х. можно построить отдельно амплитудную частотную характеристику (а. ч. х.) и фазовую частотную характеристику (ф. ч. х.). Это построение показано на рис. 2.8.
Амплитудная частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.
Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном на различных частотах.
Как следует из сказанного выше, модуль частотной передаточной функции представляет собой четную функцию частоты, а фаза – нечетную функцию частоты. Поэтому по результатам вычисления модуля и фазы для положительных частот можно сразу построить а. ч. х. и ф. ч. х. для всего диапазона частот – от до .
Можно построить также отдельно вещественную и мнимую частотные характеристики по функциям U (ω) и V (ω). Это построение показано на рис. 2.9. Как следует из сказанного выше, вещественная характеристика представляет собой четную функцию частоты, а мнимая характеристика – нечетную функцию частоты.
Минимально
– фазовые звенья и системы. В случае,
если корни числителя и знаменателя
передаточной функции W
(р)
звена
лежат в левой полуплоскости (при этом
корни числителя и знаменателя частотной
передаточной функции
![]() лежат в верхней полуплоскости), такое
звено называетсяминимально-фазовым.
Как
будет показано ниже (см.
§ 4.8),
этим звеньям присущи меньшие по абсолютной
величине фазовые сдвиги по сравнению
со звеньями, у которых это условие не
выполняется.
лежат в верхней полуплоскости), такое
звено называетсяминимально-фазовым.
Как
будет показано ниже (см.
§ 4.8),
этим звеньям присущи меньшие по абсолютной
величине фазовые сдвиги по сравнению
со звеньями, у которых это условие не
выполняется.
Можно показать [121], что для минимально-фазовых звеньев существуют следующие зависимости:
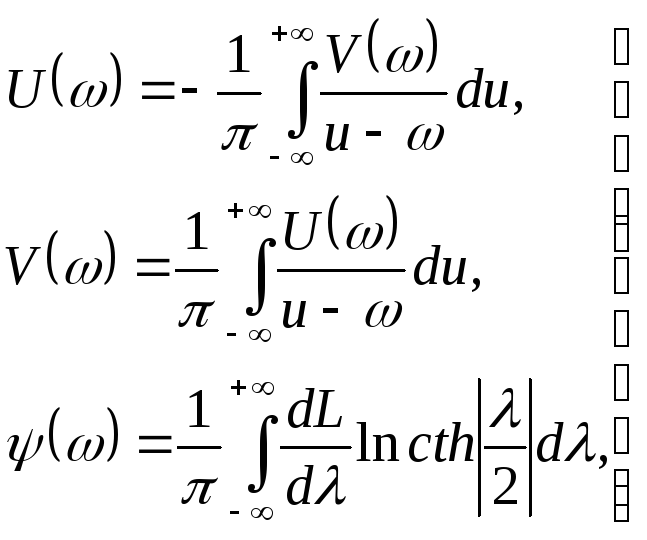 (2.17)
(2.17)
где
![]() иu
– переменная
интегрирования.
иu
– переменная
интегрирования.
Приведенные зависимости являются чрезвычайно важными, так как показывают, что частотная передаточная функция минимально-фазового звена или системы полностью определяется заданием ее вещественной части U (ω), или мнимой части V (ω), или модуля А (ω). Это позволяет упростить задачи анализа и синтеза минимально-фазовых систем, ограничиваясь, например, рассмотрением их вещественных или амплитудных частотных характеристик.
