- •3 Уравнения динамики и динамические характеристики сау
- •3.1 Общий метод составления исходных уравнений
- •3.2 Передаточные функции систем автоматического регулирования
- •3.3 Законы регулирования
- •3.4 Структурные схемы и графы
- •3.5 Многомерные системы регулирования
- •3.6 Управляемость и наблюдаемость
- •3.7 Уравнения следящей системы
- •3.8 Линеаризация уравнений
- •3.9 О записи линеаризованных уравнений звеньев
3.6 Управляемость и наблюдаемость
Рассмотрим
n-мерное пространство состояния X,
в
котором каждому состоянию системы
соответствует некоторое положение
изображающей точки, определяемое
значениями фазовых координат![]() .
.
Пусть
в пространстве состояния X
заданы
два множества
![]() и
и
![]() .
Рассматриваемая
система будет управляемой,
если
существует такое управление
.
Рассматриваемая
система будет управляемой,
если
существует такое управление
![]() ,
определенное на конечном интервале
времени
,
определенное на конечном интервале
времени
![]() ,
которое
переводит изображающую точку в
пространстве X
из
подобласти
,
которое
переводит изображающую точку в
пространстве X
из
подобласти
![]() в подобласть Г2.
в подобласть Г2.
Можно сузить определение управляемости и понимать под ней возможность перевода изображающей точки из любой области пространства состояния X в начало координат. Система будет полностью управляемой, если каждое состояние управляемо в этом смысле.
От
пространства состояния X
перейдем
к другому пространству
![]() X
посредством неособого преобразования
X
посредством неособого преобразования
![]() ,
причем
,
причем
![]() ,
где R
–
матрица коэффициентов п×п.
,
где R
–
матрица коэффициентов п×п.
Тогда вместо (3.87) будем иметь
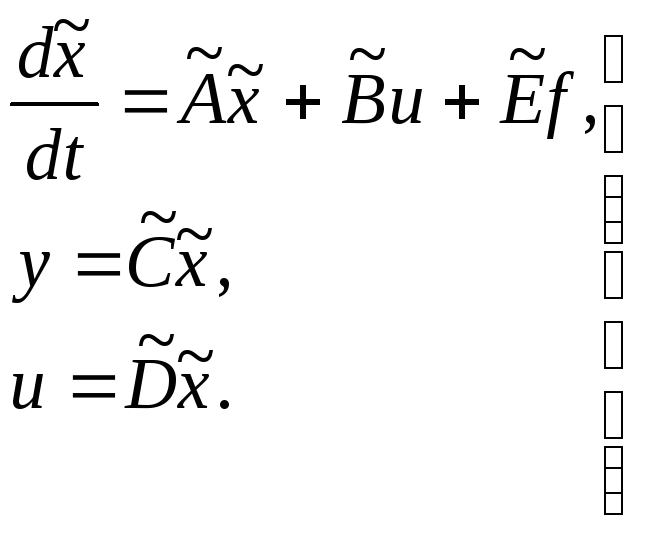 (3.91)
(3.91)
Здесь
использованы преобразованные матрицы
коэффициентов:![]() ,
,![]() ,
,![]() ,
,![]() и
и![]() .
.
Введение
новых фазовых координат посредством
неособого преобразования
![]() приводит
к эквивалентным системам различной
структуры.
приводит
к эквивалентным системам различной
структуры.
При некотором преобразовании может оказаться, что часть управляющих величин не входит в некоторые дифференциальные уравнения (3.91) или часть фазовых координат не участвует в формировании выхода у. В первом случае в система будет не полностью управляемой, а во втором – не полностью наблюдаемой.
В случае не полностью управляемой системы ее исходные уравнения могут быть представлены в виде
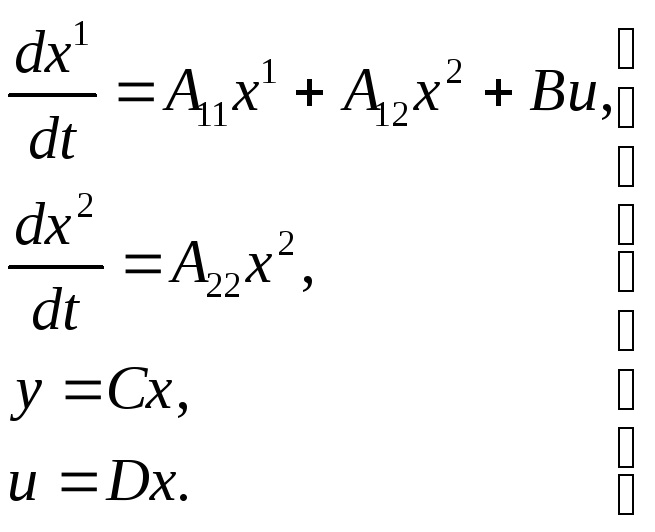 (3.92)
(3.92)
Это иллюстрирует рис. 3.15. Набор фазовых координат х1 соответствует управляемой части фазовых координат, а набор х2 неуправляемой части.
|
|
|
|
Рис. 3.15 |
Рис. 3.16 |
Р. Калманом [50] был доказан критерий управляемости, который гласит, что размерность v управляемой части системы, то есть порядок первой группы уравнений (3.91), совпадает с рангом матрицы
![]() (3.93)
(3.93)
При
![]() =
п
система
полностью управляема, при 0 <
=
п
система
полностью управляема, при 0 <
![]() <п
не
полностью управляема и при
<п
не
полностью управляема и при
![]() =
0 полностью неуправляема.
=
0 полностью неуправляема.
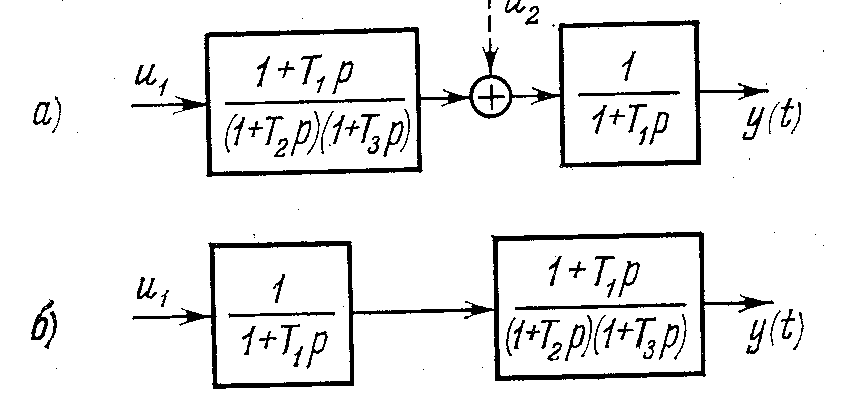
На рис. 3.16, а изображен простейший пример. Если рассматривать выходную величину у (t) при ненулевых начальных условиях, то можно записать
![]() (3.94)
(3.94)
где![]() ,
,![]() и
и
![]() ,
С1,
С2
и С3
определяются
начальными условиями до приложения
входного сигнала
,
С1,
С2
и С3
определяются
начальными условиями до приложения
входного сигнала
![]() ,а
,а
![]() – вынужденная составляющая. Система
устойчива при а>0, b>0 и с>0.
– вынужденная составляющая. Система
устойчива при а>0, b>0 и с>0.
Если
начальные условия до приложения
![]() были
нулевыми, то поведение
системы
может быть рассчитано по передаточной
функции
были
нулевыми, то поведение
системы
может быть рассчитано по передаточной
функции
![]() (3.95)
(3.95)
В этом случае по интегралу Дюамеля – Карсона
![]() (3.96)
(3.96)
Как следует из выражений (3.95) и (3.96), система во втором случае описывается дифференциальным уравнением не третьего, а второго порядка. Система будет устойчивой даже при а < 0.
Рассмотренная
система будет не полностью управляемой.
В ней оказывается, что п
=
3, а
![]() =
2.
=
2.
При
введении второй составляющей управления
![]() система оказывается полностью
управляемой, и ей будет соответствовать
матрица-строка передаточных функций
по управлению
система оказывается полностью
управляемой, и ей будет соответствовать
матрица-строка передаточных функций
по управлению
![]()
В случае не полностью наблюдаемой системы ее уравнения могут быть представлены в виде
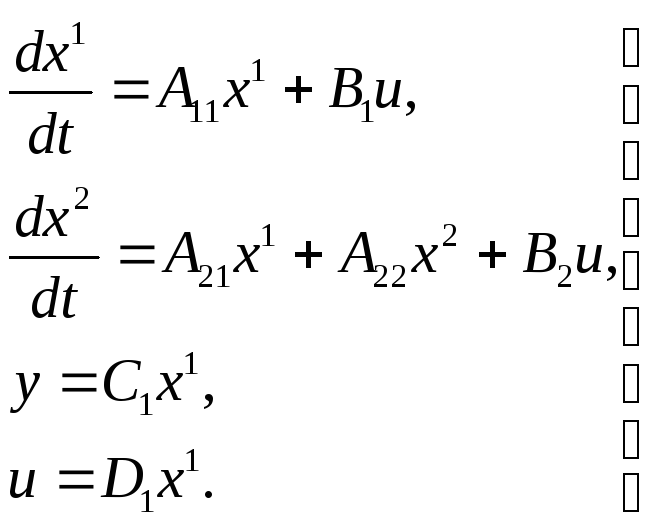 (3.97)
(3.97)
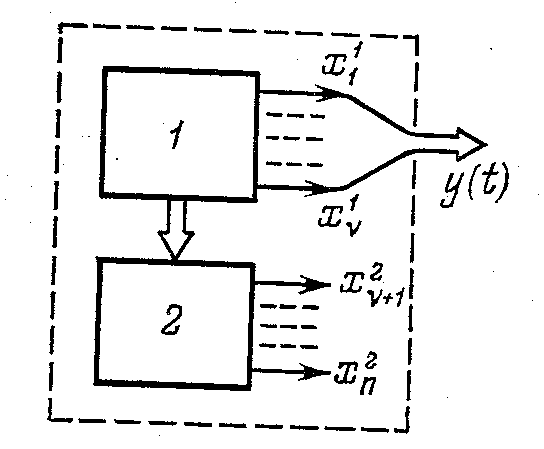
Рис. 3.17
Эти уравнения отличаются от (3.87) тем, что фазовые координаты группы х2 не входят ни в выражения для у и и, ни в первое уравнение, куда входят только фазовые координаты группы х1. Группа фазовых координат х2 относится к ненаблюдаемым. Это иллюстрирует рис. 3.17.
Р.
Калманом [50]
показано, что порядок первой группы
![]() уравнений
совпадает
с рангом матрицы
уравнений
совпадает
с рангом матрицы
![]() (3.98)
(3.98)
При
![]() =п
система
полностью наблюдаема, при 0 <
=п
система
полностью наблюдаема, при 0 <
![]() <
п
–
не полностью наблюдаема в при
<
п
–
не полностью наблюдаема в при
![]() =
0 полностью ненаблюдаема.
=
0 полностью ненаблюдаема.
На рис. 3.16, б изображен простейший пример. Для него легко показать, что в формировании выхода участвуют только две фазовые координаты из трех.
В общем случае система может содержать четыре группы фазовых координат: управляемую, но ненаблюдаемую часть х1, управляемую и наблюдаемую часть х2, неуправляемую и ненаблюдаемую часть х3 и неуправляемую, но наблюдаемую часть х4.
Исходные уравнения системы (3.87) в этом случае можно для самого общего случая записать следующим образом:
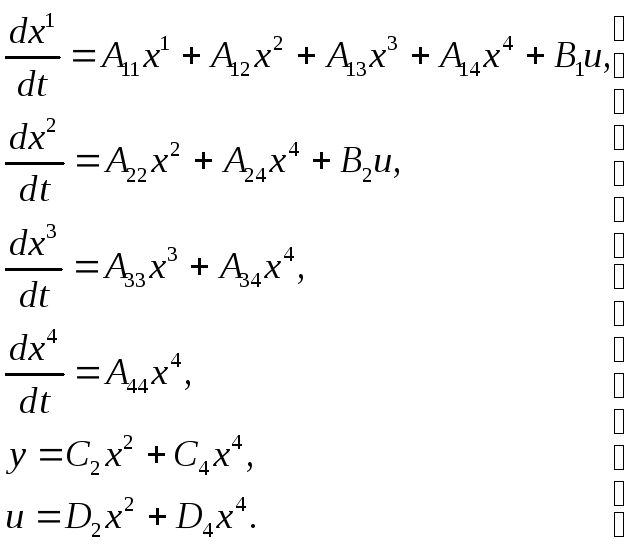 (3.99)
(3.99)
Левая часть характеристического уравнения (3.88) системы в этом случае содержит четыре сомножителя:
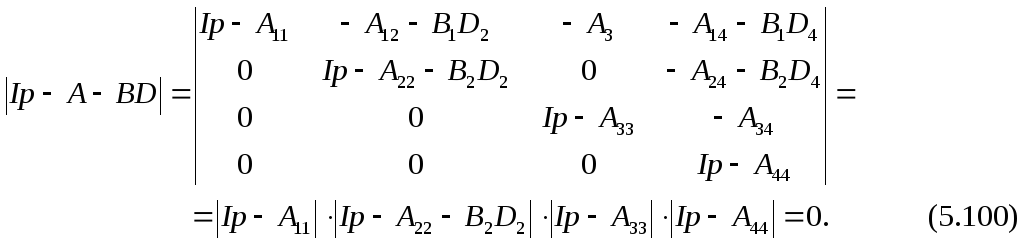 (3.100)
(3.100)
Управляемость и наблюдаемость системы в изложенном смысле не всегда совпадает с практическими представлениями. Даже если какая-либо фазовая координата и может быть вычислена по доступным для измерения выходным величинам, обработка измеренных величин может быть, во-первых, сложной и, во-вторых, она может быть затруднена наличием помех. Поэтому практически наблюдаемыми координатами обычно считаются те из них, которые могут быть непосредственно измерены датчиками различных типов.