4.2 Методы определения критериев подобия

В соответствии с приведенными теоремами подобия критерии подобия определяются в основном двумя способами. Первый заключается в приведении уравнений физического процесса к безразмерному виду. Следовательно, чтобы его применять, нужно иметь уравнение исследуемого процесса. Второй способ базируется на применении π – теоремы. Им можно пользоваться в случаях, когда известны только параметры, участвующие в исследуемом процессе, а уравнения процесса неизвестны.

На практике пользуются также третьим способом относительных единиц, являющихся модификацией первых двух способов [3,6,8]. Наиболее существенные параметры, выраженные в долях от базисных, можно рассматривать как своего рода критерии подобия, действующие в данных конкретных условиях.

4.2.1 Определение критериев подобия путем приведения уравнения к

безразмерному виду (способ интегральных аналогов)

Данный способ является более простым и точным, так как используются уравнения, описывающие физический процесс, а также условия однозначности. С указанным методом мы уже познакомились ранее, когда выводили критерий Ньютона, используя второй закон динамики. Продемонстрируем его при рассмотрении физического подобия механических систем.

Подобие механических систем.Рассмотрим случай вынужденных механических колебаний с демпфированием. Пусть груз массой М (рис.4.2) колеблется на пружине жесткостью ε (Н/м), дающей упругое сопротивлениеF_y= -c·S, причем при его перемещении на расстояниеS(м) появляется вязкое сопротивление, пропорциональное скоростиV(м/с):

F_c = - k·V,

где k– коэффициент пропорциональности, Н· с/м.

На груз действует возмущающая сила (Н) F_b=F·sinωt, гдеω– угловая частота колебаний,I/с;t– время, с. Дифференциальное уравнение имеет вид

. (4.5)

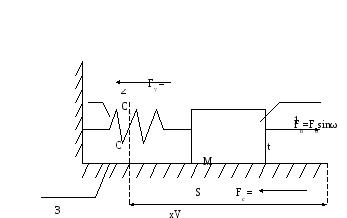
Рис. 4.2 Схема движения механической системы :

1 – масса; 2 – пружина; 3 – опора; F_b– возмущающая сила;F_y– упругая

сила; F_с– сила вязкого сопротивления.

Разделим все члены уравнения (4.5) на первый член и примем, имеем:;

;;

π₄= ω·t= Н₀ =1. Критерий Н₀(гомохронности) характеризует изменение процесса и в данном случае имеет смысл при условии, что воспроизводится изменение силыF_bименно по синусоидальному закону с частотой ωt. При преобразованиях мы не учитывалиsinωt, так как тригонометрические функции в геометрическом подобии имеют одинаковые значения углов, поэтому тождественно равны.

Согласно второй теореме подобия уравнение движения груза под действием приложенных сил представляем функциональной зависимостью, составленной из критериев подобия:

Ф(π₁,π₂,π₃,π₄)=0

или

. (4.6)

4.2.2 Разработка математической модели механической системы

(на примере ФМС «МРТ – ВСП»)

Решение задач по оптимизации и диагностики существующих механических систем машин и механизмов, а также задачи по прогнозированию параметров вновь создаваемых механических систем неразрывно связаны с решением вопросов идентификации их параметров. Это связано с существенным взаимным влиянием динамических процессов, протекающих в механических системах путевых машин на работу функциональных узлов (пара сцепления «колесо – рельс», фрикционные муфты, тормоза и т.д.), входящих в их состав. В ряде случаев изменение параметров механической системы может привести к изменению на целый порядок выходных триботехнических параметров узла трения (коэффициента трения и стабильности его значений, износостойкости) [4].

Математическая модель механической системы по сравнению с реальным объектом имеет ряд преимуществ. В ней отсутствуют (при корректной постановке задачи) дополнительные элементы и факторы, провоцирующие не предусмотренные в исследовании процессы, преодолеваются сложности связанные с получением информации о реальном объекте (например, размещение датчиков в труднодоступных местах и пр.). Математическая модель допускает многократное повторение математического эксперимента при различных значениях параметров исследуемой механической системы. Основной принцип при построении математической модели заключается в следующем: математическая модель должна наиболее полно отражать исследуемые свойства реального объекта, при этом сложность ее должна быть минимальной.

С учетом изложенного целью математического моделирования является установление закономерностей изменения основных динамических характеристик в зависимости от изменения параметров состояния механической системы, а также уточнение информативного признака при оптимизации тяговых характеристик путевой машины.

Поставленная цель достигается путем решения следующих задач :

1. Обоснование структуры и определение параметров математической модели.

2. Математическая формализация динамической системы.

Математическая модель механической системы состоит из расчетной схемы и математического аппарата, описывающего движение динамической системы.

При исследовании движения путевой машины, как механической системы, взаимодействующей с железнодорожным путём, экипаж, колесные пары, вне зависимости от их конструкции, чаще всего рассматривают как элементы, обладающие лишь определённой массой (m), сосредоточенной в центре тяжести элемента, при этом весьма редко эти элементы рассматриваются как конструкции, имеющие определённым образом распределённые в пространстве массы и жёсткости.

Конструкции и параметры связей между экипажем и колёсной парой чрезвычайно разнообразны; влияние же этих связей на динамические процессы взаимодействия подвижного состава и пути весьма велико. Поэтому при исследовании динамики путевой машины особое внимание уделяется основным принципиальным схемам и параметрам этих связей.

Источником всех динамических возмущений в пути и подвижном составе является колёсные пары, которые при своём движении по рельсам и стрелочным переводам совершают сложные пространственные перемещения и тем самым заставляют колебаться на рессорном экипаж и сам путь.

Дополнительные динамические вертикальные силы, передаваемые колесом путевой машины рельсу, вызванные колебаниями надрессорного строения (экипажа), не должны превышать статическую нагрузку кузова на колесо. Если эти силы достигнут величин, равных статической нагрузке на колесо (104...167 кН), то при колебаниях надрессорного строения будут возникать такие же силы разгрузки колеса, то есть произойдёт полное обезгруживание колеса. Это крайне опасно, поскольку обезгруженное колесо может сойти с рельса.

Силы же, возникающие от инерции необрессоренных масс могут достигать нескольких сотен кН. Причинами появления сил инерции необрессоренных масс являются неровности на пути и неровности на поверхности катания колёс. Эти неровности делят на изолированные и непрерывные, короткие и длинные. При движении путевой машины по звеньевому рельсовому пути, соединённому в стыках накладками, всегда возникают соударения колёс с рельсами.

Поэтому при проектировании путевых машин особое внимание должно уделяться их динамическим воздействиям на железнодорожный путь.

Для изучения динамических свойств примем в качестве подвижной единицы базовую путевую машину мотовоз МПТ с конструкционной скоростью движения до 100 км/ч, движущегося по участку однородного упругого пути произвольного очертания в плане. Упруго-инерционные свойства пути в вертикальном и поперечном направлениях учитываются присоединением к каждому колесу приведенной массы пути.

Расчетная схема для построения математической модели проектируемого экипажа путевой машины представлена на рис.4.3 в виде дискретной механической системы, состоящей их трех твердых тел: кузова и двух колесных пар. Кузов через упруго-диссипативные элементы опирается на буксы колесных пар.

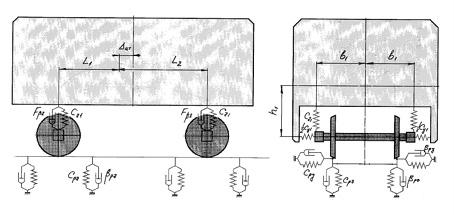
Рис. 4.3 Расчетная схема экипажа типа мотовоза МПТ

Для составления системы дифференциальных уравнений вынужденных колебаний воспользуемся общим уравнением динамики материальной системы в обобщённых координатах (работа внешних, внутренних и инерционных сил, действующих на движущееся тело при вариации координат его траектории, должна равняться нулю ) и примем, как и в расчетах математической системы путевой машины, за основу уравнение Лагранжа второго рода в виде:

, (4.7)

где - число степеней свободы;

Т, П – кинетическая и потенциальная энергии системы;

Ф – функция рассеивания энергии системы;

- обобщенные координаты и их производные;

- обобщенные внешние силы.

При составлении математической модели путевой машины принимаем следующие допущения:

1. Все тела механической системы модели абсолютно твердые. Принимаем, что в расчетной схеме имеется три твердых тела – кузов, который через упруго-диссипативные элементы опирается на буксы двух колесных пар.

2. Колеса в вертикальной плоскости совершают колебания совместно с рельсами.

При составлении математической модели путевой машины полагаем, что путевая машина движется по участку однородного упругого пути произвольного очертания в плане. Упруго-инерционные свойства пути в вертикальном и поперечном направлениях учитываются присоединением к каждому колесу приведенной массы пути.

Для рассматриваемой механической системы положение в пространстве модели кузова путевой машины полностью определяется следующими координатами – боковой относ у_к, подпрыгиваниеz_к, боковая качка_к, галопирование_к и виляние_к, то есть кузов имеет пять степеней свободы. Колесная пара имеет четыре степени свободы: боковой относ у_кпi, подпрыгиваниеz_кпi, боковая качка_кпiи виляние_кпi. Приведенная масса пути (рельс) под каждое колесо имеет одну степень свободы – поперечное перемещение у_оij(i=1, 2;j=1, 2). Вертикальные перемещения рельсовz_oij, учитывая принятое допущение 2, рассчитываются как совместные линейные перемещения рельсов под колесом. Таким образом, рассматриваемая система имеет 17 степеней свободы:

у_к, у_кп1 , у_кп2,z_к,z_кп1,z_кп2,_к,_кп1,_кп2,_к ,_к, ,_кп1,_кп2, у₀₁₁, у₀₁₂, у₀₂₁, у₀₂₂и рассматривается материальная система, подчинённая идеальным голономным связям.

В соответствии с принятой расчетной схемой кинетическая энергия Т системы ТПС (тяговый подвижной состав) – верхнее строение пути определяется из выражения

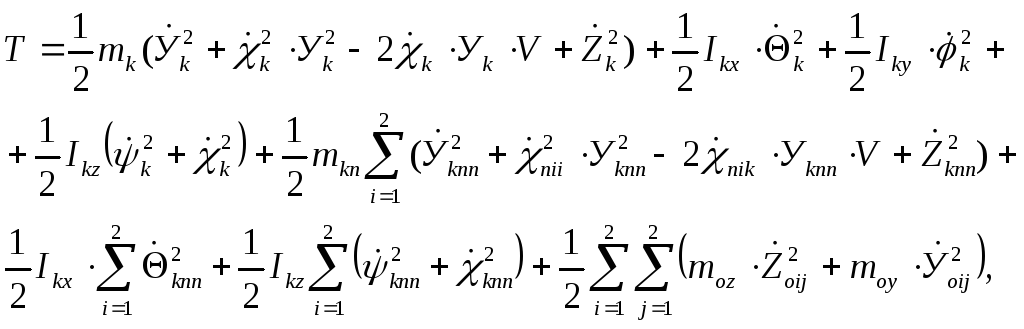(4.8)

где - скорость движения путевой машины;

- углы изменения траектории движения (в плане) соответствующих тел: кузова и колесных пар, в круговой кривой радиусаR_o;

- угловые скорости изменения траектории движения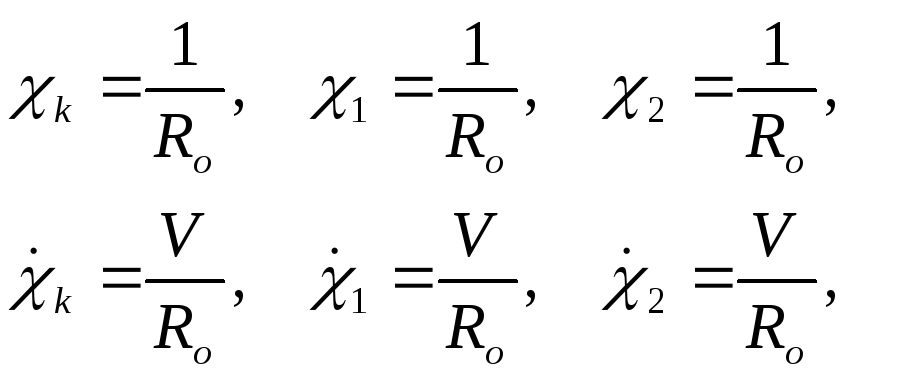

- радиус кривизны пути в плане (для кривых).

Для прямых .

Потенциальная энергия определяется как сумма энергий упругих деформаций и изменения энергии вследствие подъема или опускания центров тяжести тел входящих в систему.

Линейные перемещения упругих элементов буксового рессорного подвешивания путевой машины, которые записываются в следующем виде - в поперечном направлении

- в вертикальном направлении

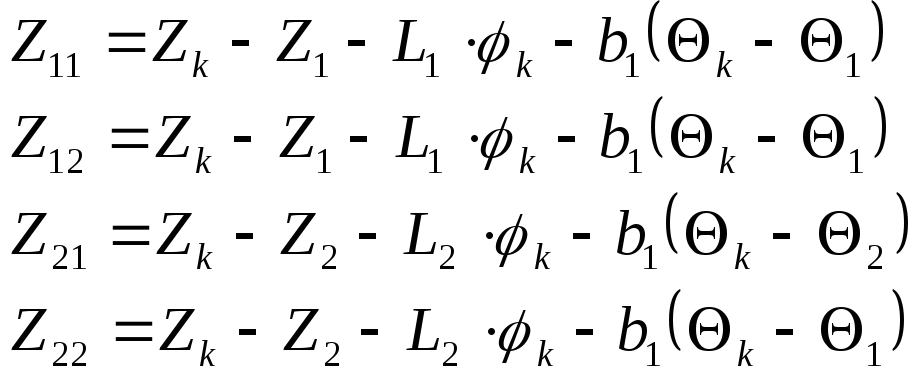
- в продольном направлении

Вертикальные линейные перемещения рельсов под- колесом записываются в следующем виде:

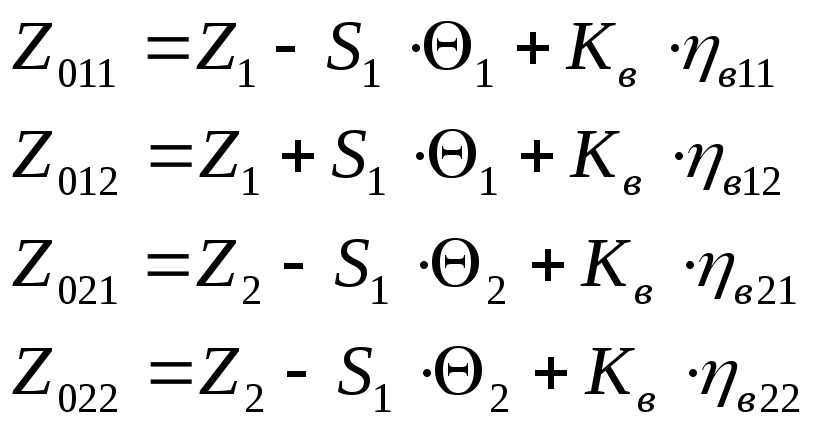
где - вертикальные неровности пути,

- коэффициент уровня вертикальной неровности пути

Потенциальная энергия системы П определяется из выражения

(4.9)

Функция рассеивания энергии системы Ф определяется из выражения

(4.10)

- функция определения знака

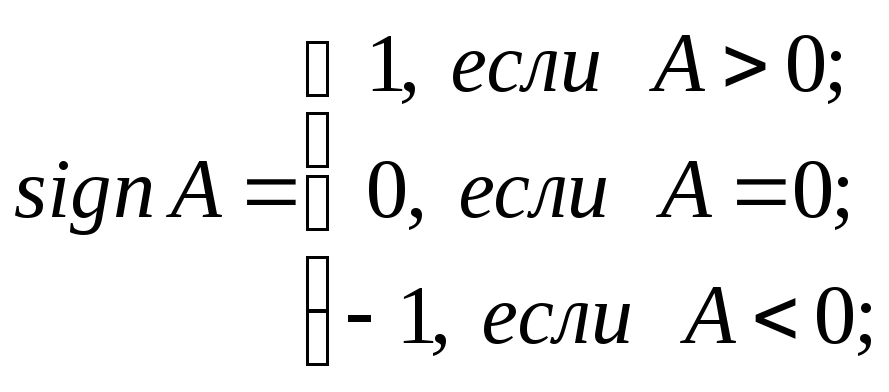
- коэффициент демпфирования пути в вертикальном направлении;

- коэффициент демпфирования пути в горизонтальной плоскости.

Выражения относительных скоростей проскальзывания колес в продольноми в поперечномнаправлениях, необходимых для определения сил взаимодействия колес с рельсами, записываются следующим образом:

где - приращение радиусов кругов катания колес при их поперечных перемещениях относительно рельсовых нитей, определяемых из следующего выражения:

где - константы, характеризующие профиль колеса,

- поперечные линейные перемещения колесных пар относительно рельса записываются в следующем виде:

,

- поперечные неровности пути,

- коэффициент уровня поперечной неровности пути.

Касательные силы взаимодействия колес с рельсами согласно гипотезе крипа нелинейно зависят от безразмерных характеристик проскальзываний

.

Эти силы с достаточной точностью определяются из выражения:

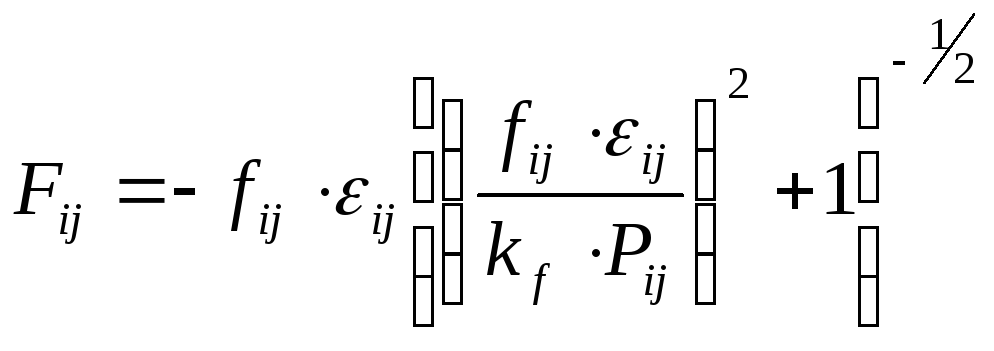
где - коэффициенты псевдоскольжения, значения которых определяются из выражения (формула эмпирическая, поэтому значения величины выражено в тоннах силы технической системы единиц)

- коэффициент трения скольжения стали по стали;

- вертикальные нагрузки, действующие на рельсы подij- колесами, определяемые следующим образом:

.

Продольные и поперечныесоставляющие силопределяются из равенств

.

Поперечные составляющие вертикальных сил, действующих на колеса вследствие криволинейного очертания их профиля, определяются из выражения:

,

где .

Рамные силы, то есть горизонтальные силы, действующие через буксы на колесные пары, определяются из выражения:

.

Коэффициенты вертикальной динамики определяются из выражения:

,

где - статический прогиб рессорного подвешиванияI-ой колесной пары.

Подставляя выражения (4.8, 4.9, 4.10), полученные для кинетической и потенциальной энергий, функции рассеивания в уравнения Лагранжа 11 рода (4.7), получена система (4.11), состоящая из 17 нелинейных дифференциальных уравнений 2-го порядка, описывающих движение экипажей проектируемых путевых машин с постоянной скоростью по пути произвольного очертания в плане:

1.

2.

3.

4.

5.

6.

7.

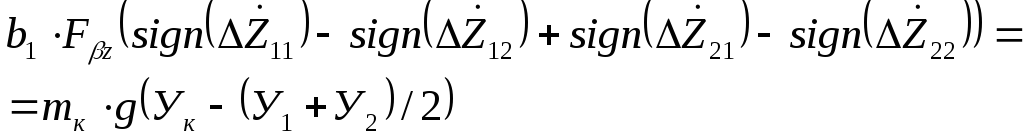
8.

9.

10.

11.

+

12.

13.

14.

15.

16.

17. (5.11)