Тема 4 Показатели вариации

§ 4.1. Размах вариации r

Средние величины не являются универсальными характеристиками варьирующих объектов. При одинаковых средних признаки могут отличаться по величине и характеру варьирования. Поэтому наряду со средними для характеристики варьирующих признаков используют так же показатели вариации. Одним из таких показателей являются лимиты (от лат. limes – предел). В биометрии под этим термином понимают значения минимальной x_min и максимальный x_max вариант совокупности.

Размах вариации R представляет собой разность между максимальной и минимальной вариантами совокупности, т.е. . Чем сильнее варьирует признак, тем больше размах вариации, и, наоборот, чем слабее вариация признака, тем меньше будет размах вариации.

Лимиты и размах вариации – простые и наглядные характеристики варьирования, однако им присущи существенные недостатки:

• при повторных измерениях однако и того же группового объекта они могут значительно изменятся;

• они не отражают существенные черты варьирования.

Например, возьмем два ряда распределения с одним и тем же весом входящих в их состав вариант, равным единице:

x1	10	15	20	25	30	35	40	45	50
x2	10	28	28	30	30	30	32	32	50

По числу вариант (n = 9), лимитам и размаху вариации эти ряды не отличаются друг от друга; их средние также равны между собой. Отличает их друг от друга характер варьирования, но эта особенность никак не отражается на лимитах и размахе вариации.

Более удобной характерной вариации мог бы служить показатель, который строится на основании отклонений вариант от их средней, т.е. 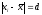. Сумма таких отклонений, взятая без учета знаков и отнесенная к числу наблюденийn, называется средним линейным отклонением .

Так, если взять суммы отклонений вариант от их средней от их средней () для первогоx₁ и второго x₂ приведенных здесь рядов, то получим следующие результаты:

d1 = 20	15	10	5	0	5	10	15	20	∑d1 = 100
d2 = 20	2	2	0	0	0	2	2	20	∑d2 = 48

Отсюда и. Таким образом в первом случае варьирование сильнее, чем во втором.

§ 4.2 Дисперсия s2 и ее свойства

Несмотря на явное преимущество среднего линейного отклонения перед лимитами и размахом вариации, этот показатель не получил широкого применения в биометрии. Наиболее подходящим оказался показатель, построенный не на отклонениях вариант от их средних, а на квадратах этих отклонений, его называют дисперсией (от лат. dispersio – рассеяние) и определяют по формулам:

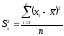или (12)

, (13)

где x_i – i-я варианта; – среднее значение; f_i – частоты или веса; k – класс; n – общее число наблюдений.

Преимущество дисперсии заключается:

Во-первых, в том, что, являясь мерой варьирования числовых значений признака вокруг их средней арифметической, она измеряет и внутреннюю изменчивость значений признака, зависящую от разности между наблюдениями.

Во-вторых, дисперсия разлагается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на величину учитываемого признака.

Но вместе с тем установлено, что рассчитываемая по формуле (13) дисперсия оказывается смещенной по отношению к своему генеральному параметру на величину, равную . Чтобы получить не смещенную дисперсию, нужно в формулу (13) ввести в качестве множителя поправки на смещенность, называемуюпоправкой Бесселя. В результате формула (13) преобразуется следующим образом:

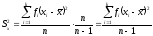(14)

Разность , в дальнейшем обозначаемаяk, называется числом степеней свободы, под которым понимают число варьирующих единиц в составе численно ограниченной статистической совокупности.

Так, если совокупность состоит из n-го числа членов и характеризуется средней величиной , то любой член этой совокупности может иметь какое угодно значение, не изменяя при этом среднюю, кроме одной варианты, значение которой определяется разностью между суммой значений всех остальных вариант и величиной. Следовательно, одна варианта численно ограниченной статистической совокупности не имеет свободы вариации. Отсюда число степеней свободы для такой совокупности будет равно. А при наличии не одного, а нескольких ограничений свободы вариации число степеней свободы вариации будет равно, гдеν – обозначается число ограничений свободы вариации.

Дисперсия обладает рядом важных свойств:

1. Если каждую варианту совокупности уменьшить или увеличить на одно и тоже постоянное число A, то дисперсия не изменится:

Отсюда следует, что дисперсию можно вычислять не только по значениям варьирующего признака, но и по их отклонениям от какой-либо постоянной величины A (например, предельно допустимой концентрации вредного вещества в какой-либо среде).

2. Если каждую варианту совокупности разделить или умножить на одно и тоже постоянной число A, то дисперсию уменьшается или увеличивается в A² раз.

Доказательство:

А также:

Из этого свойства следует, что при наличии в совокупности многозначных вариант их можно сократить на какое-то постоянное число A и по полученным результатам вычислить дисперсию. Затем полученную величину умножить на квадрат общего делителя A², что даст искомую величину дисперсии.

На основании математических свойств средней арифметической и дисперсии нетрудно составить сводку правил по преобразованию многозначных и дробных чисел, которую полезно использовать при обработке биометрических данных (табл.9).

Таблица 9

Способы преобразования чисел	Какие поправки нужно внести в конечный результат
	при вычислении дисперсии	при вычислении средней арифметической
x-A	поправка не нужна	прибавить число A
(x-A)K	разделить на K2	разделить на K и прибавить число A
(x-A)/K	умножить на K2	умножить на K и прибавить число A
x/К	умножить на A2	умножить на число A
xA	разделить на A2	разделить на число A

В этой таблице A – произвольно взятое число, обычно близкое к величине минимальной варианты x_min; K – произвольное число, позволяющее преобразовывать дробные числа; x – отдельные числовые значения признака, т.е. варианты.

Следует также иметь в виду, что вместо можно использовать; или

Отсюда можно вывести следующие рабочие формулы, удобные при вычислении дисперсии непосредственно по значениям варьирующего признака:

или при повторяемости отдельных вариант: