5.4. Основные теоремы о вычетах

5.5. Вычисление определенных интегралов с помощью вычетов

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

TERECSHENKO.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

611.32 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1411 12 13 14 > Следующая >>>

z2 sin

= z2

æ 1

1 1

= z -

1 1

-K.

-K÷

3! z3

5! z5

3! z

5! z3

è z

Следовательно, вычет [ f (z); z = 0] = c

= -

−1

Особая точка

z0 =1 полюс второго порядка (т.к.

z0 =1 нуль порядка две функции

g(z) =

). По формуле (10.1) получим при n=2,

f (z)

×(z -1)

выч.[ f (z); z =1] = limç

÷ = lim3z2 = 3 .

(z -1)

z→1

z→1è

Задачи для самостоятельного решения

5.2. Найти вычеты в конечных особых точках следующих функций.

tgz

а) f (z) =

;

б) f (z) = z4e z ;

в) f (z) =

;

z2 (z -1)

+ z3 ;

1- cos z

г)

f (z) = cos

д)

f (z) =

; е)

f (z) = e

z−1

;

z3(z - 2)

ж)

f (z) =

e z

;

к)

f (z) =

sin z

;

л)

f (z) =

ezi

1+ z

sin pz

Теорема 1. Пусть функция f(z) аналитическая в области G за исключением конечного числа изолированных особых точек z1, z2,K, zn , лежащих в этой области.

Тогда справедливо равенство

	n
!ò f (z)dz = 2πiåвыч[ f (z); z = zk ],		(5.7)
Γ+	k =1

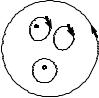
где Г – контур, лежащий внутри области D и содержащий внутри себя точки z1, z2,K, zn . Доказательство. Опишем вокруг каждой из точек zk окружности γk :| z - zk |= ρ столь

малого радиуса, чтобы круг | z - zk |£ ρ содержался в G и каждая окружность γk лежала во внешности всех остальных (рис.5.1). Функция f(z) аналитическая в области G1 , получае

z2 z1

Рис.5.1.

мой из G удалением всех кругов | z - zk |£ ρ . В силу теоремы Коши о составном контуре

	n
!ò f (z)dz = å!ò f (z)dz , но
Γ+	k =1 γk

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

!ò f (z)dz = 2πi выч[ f (z); z = zk ],

γk

следовательно

	n
!ò f (z)dz = 2πiåвыч[ f (z); z = zk ].		(5.8)
Γ+	k=1

Теорема 2. Если функция f(z) – аналитическая на всей комплексной плоскости, за ис-

ключением точек z1, z2,K, zn−1, zn = ¥ , то имеет место равенство åвыч[ f (z); z = zk ] = 0 .

k =1

Доказательство. Выберем контур γ , охватывающий точки z1, z2,K, zn−1 . Тогда по теореме 1, получим, что

	n−1
!ò f (z)dz = 2πiåвыч[ f (z); z = zk ] = -!ò f (z)dz =
Γ+	k=1	−Γ

= -2πi выч[ f (z); z = ¥],

т.е.

åвыч[ f (z); z = zk ] = 0 .

k =1

Пример. Вычислить интегралы с помощью вычетов

1. !ò

ez dz

; 2.

!ò

ez dz

; 3.

!ò

-1

-1)(z +

|z−1|=

|z−1|=3

-1

|z+1|=

Решение: 1) Точки

= -1, z

- простые полюсы f (z) =

, из них только точка

z2 -1

z=1, попадается в область ограниченную контуром, поэтому

!ò

ez dz

e z

æ ez

= eπi .

= 2πi вычê

; z =1ú

= 2πi ×ç

-1)

ê z

-1

ç 2z

øz=1

|z−1|=

2) Точки z1 = -1, z2 =1 попадают в область ограниченную контуром, поэтому

!ò

ez dz

e z

é e z

ùö

= 2πiçвыч

; z = -1ú +

вычê

; z =1ú÷ =

2 -

-1

ê z

ê z2 -1

ú÷

|z−1|=3

ûø

= 2πi ×

- e

−1

πi(e

-1)

÷ =

è 2

3) Функция

f (z) =

имеет внутри контура | z +1|=

четыре особые точки –

(z4 -1)(z + 2)

2, –1, i и –i, а во внешности контура – только одну, именно 1. Сумма вычетов в особых точках внутри контура, в силу доказанной теоремы, отличается только знаком от суммы вычетов во внешности окружности | z +1|=1,5 . Следовательно,

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

!ò	f (z)dz = -2πi(выч( f (z); z = ¥) + выч[ f (z); z =1]) .
\|z+1\|=	3
	2

Но вычет f(z) в точке z = ∞ равен нулю, т.к. в разложении f(z) в окрестности z = ∞ нет сте-

пени с z−1 .

Точка z=1 – простой полюс, поэтому:

выч[ f (z); z =1] = lim

z -1

+1)(z2

z→1 (z -1)(z

+1)(z + 2)

После преобразований, получим

!ò

πi

= -

(z4 -1)(z + 2)

|z+1|=

Задачи для самостоятельного решения

ez dz

5.3. С помощью вычетов вычислить интегралы

а)

;

б)

!ò

z2 sin

dz ;

в)

!ò

zdz

;

(z +1)

|z+1|=4 e

+ 3

г)

ezdz

;

д)

|z|=2

cos2 z -1

;

е)

z - sin z

dz ;

!ò z

+ 2z

!ò

|z−i|=1

|z|=2

|z|=1

e2z - z

ez - sin z

ж)

!ò

dz ;

к)

;

л)

!ò

dz ;

|z|=1

|z|=3

|z|=1/ 3

м)

dz ;

н)

!ò

eiz

+ 2

dz ;

о)

;

|z|=1 sin 3zi

|z−1|=3

|z|=4 e +

п) !ò

+ cos z

dz .

|z|=3

(x -1)cos5x

dx = -π ×e−10 ×cos5 .

По формуле (5.12) получим ò

Вычеты успешно применяются для вычисления определенных интегралов. Рассмот- рим некоторые наиболее характерные случаи применения вычетов.

2π

1. Вычисление интегралов ò R(cosj,sin j)dj, где R(u,v) – непрерывная рациональная

функция. Для вычисления интеграла с помощью вычетов, введем замену z = eiϕ , 0 £ j £ 2π . При изменении ϕ на промежутке [0;2π] , точка z один раз обойдет окружность радиуса 1 в

положительном

направлении.

Заменяя

по

формулам

Эйлера

1 ö

1 æ

1 ö

, и dj =

преобразуем заданный интеграл к контурному

cosj =

ç z +

, sinj =

ç z -

z ø

2i è

z ø

интегралу

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

2π

ò R(cosj,sin j)dj = !ò

R1(z)dz ,

(5.9)

где

|z|=1

R (z) =

æ 1

æ z -

1 ö

æ z +

öö .

÷÷

è 2i è

z ø

z øø

Для вычисления последнего интеграла применима основная формула теории вычетов:

!ò	n
!ò	R1(z)dz = 2πiåвыч[R1(z); z = zk ].	(5.10)
\|z\|=1	k =1

В формуле (5.10) учитываются только те особые точки zk , для которых выполнено нера- венство | zk |<1.

2π	dj
Пример. Вычислить ò	dj
		.
	cosj - 2	.
0
Решение. Так как подинтегральная функция			1	непрерывна на отрезке [0;2π] , то
Решение. Так как подинтегральная функция			cosj - 2	непрерывна на отрезке [0;2π] , то

интеграл существует. Полагая z = eiϕ ,dj = dziz , получим:

2π

!ò

cosj - 2

æ z + z

−1

- 4z +1

|z|=1

- 2

|z|=1

z ç

Функция

имеет два простых полюса z1 = 2 + 3, z2 = 2 - 3 (нули знамена-

R(z) =

4z +

теля). Так как | z1 |>1, а | z2 |<1, то внутрь контура попадает только z2 , поэтому:

2π

× 2πi ×вычê

; z

= z2 ú .

cosj - 2

ë z

- 4z +1

Вычет удобно вычислять, используя разложение квадратного трехчлена на множители,

именно

выч

; z = z

= lim

(z - z2 )

- 4z

(z - z )(z - z

)

- z

z→z2

ë z

2π

-2

Окончательно получим ò

cosj -

+∞

P (x)

2. Вычисление интегралов

dx , где Pm (x),Qn (x)

многочлены степени m и n,

Q (x)

−∞

причем n ³ m + 2,Qn (x) ¹ 0

на действительной оси. Для вычисления интеграла с помощью

вычетов введем функцию

F(z) =

Pm (z)

. Особые точки этой функции это полюса - нули

Q (z)

знаменателя, они расположены внутри некоторого круга

| z |< R0 ,

где R0 – достаточно

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

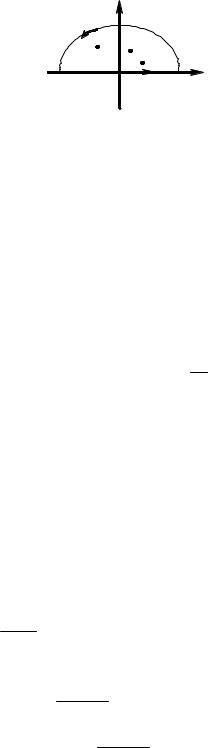
большое число. Для применения теоремы о вычетах						возьмем замкнутый контур CR
(рис.5.2),
				y
					G+
				z2	R
			z1	z2	zs
			–R	0	R	x
			Рис.5.2.
который состоит из полуокружности G+				:\| z \|= R,Im z ³ 0 ,			где R > R	и отрезка действи-
			R				0
тельной оси -R £ x £ R, CR = GR + G1 . Если обозначить через							z1, z2 ,K, zs	все различные по-
люсы F(z) в верхней полуплоскости, то получим
	R		s
!ò F(z)dz = ò F(x)dx + ò F(z)dz = 2πiå выч [F(z); z = zk ]. (5.11)
CR+	−R	Γ+R	k =1 Im zk >0
Покажем,	что при	R ® ¥ предел ò F(z)dz		равен нулю.			Так как степень знаменателя
			ΓR+
n ³ m + 2 , то функция z2 × F(z)			ограничена в окрестности точки z = ∞ , поэтому

| z2F(z) |£ M , | z |³ R1,| F(z) |£ M2 ,

где

		\| z \|= R > max(R0 , R1) .
Поэтому
		F(z)dz	£	M	× πR =	πM	® 0, R ® ¥ .
	ò
				2		R
	Γ+R			R

Переходя в равенстве (5.11) к пределу при R → ∞ , получим

+∞ P (x) −∞ò Qmn (x)

Пример. Вычислить интеграл

dx = 2πiå выч

k=1 Im zk >0

+∞

ò dx .

−∞ (x2 +1)2

é Pm (z)		ù
ê		; z = zk ú .
	Q (z)
ë n		û

Решение. Подинтегральная функция (x2 +1)2 удовлетворяет условиям применения

теории вычетов: Pm (x) =1,m

+∞

−∞

= 0, P (x) = (x2 +1)2 ,n = 4 n ³ 2 , поэтому
		n
		dx		s	é			1		ù
		dx		= 2πiå выч	é			1		ù
					ê					; z = zk ú .
(x	2	+1)	2		ê	(z	2	+1)	2	; z = zk ú .
(x		+1)		k =1 Im zk >0	ë	(z		+1)		û

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

В верхней полуплоскости находится особая точка z=i – полюс второго порядка, следова-

тельно

+∞

−∞

Так как

dx	é	1	ù
	= 2πi ×вычê		; z = iú .
(x2 +1)2	= 2πi ×вычê	(z2 +1)2	; z = iú .
(x2 +1)2	ë	(z2 +1)2	û

(z - i)

ö¢

вычê

; z = iú

= limç

÷ = lim-

ë(z

+1)

z→i

- i)

(z + i)

z→i

(z + i)

то

+∞

−∞

+∞ P (x)

P (x)

Замечание. При вычислении интегралов

dx , где F(x) =

четная функция,

Q (x)

необходимо использовать равенство

+∞

P (x)

+∞

P (x)

dx .

Q (x)

(x)

−∞

+∞	+∞
3. На практике часто встречаются интегралы вида ò f (x)cosαxdx ,	ò f (x)sin αxdx , где
−∞	−∞

α > 0 – параметр. Эти интегралы (при условии, что они существуют) можно рассматривать

+∞

как действительную и мнимую части комплекснозначной функции

ò eiαx f (x)dx . Для вы-

−∞

числения последнего

интеграла

можно

применить

теорию

вычетов к

функции

F(z) = eiαz f (z) при условии, что справедлива лемма Жордана.

Лемма.

Пусть

функция

f(z)

непрерывна

при

| z |³ R0 > 0,Im z ³ 0,α > 0

MR = max | f (z) |® 0 при R → ∞ , тогда ò

f (z)eiαz dz ® 0 при R → ∞ .

zΓR

ΓR

Доказательство.

Оценим интеграл

ò eiαz f (z)dz . Так

как

на полуокружности

ΓR

GR , z = Reiϕ ,0 £ j £ π , то

dz = i Reiϕ dj,| eiαz |=

eiαR(cosϕ+i sin ϕ)

= e−αR sin ϕ ,

поэтому

ò eiαz f (z)dz

£ M R × Ròe−αR sin ϕdj .

ΓR

График функции sin ϕ

на отрезке

0 ≤ ϕ ≤ π

симметричен относительно прямой

j =

sin j ³

j при 0 £ j £

. Следовательно, с учетом условия α > 0 получим

π / 2

2αR

(1- e−αR ).

òe−αR sin ϕdj = 2 ò e−αR sin ϕdj £ 2 ò e−

π ϕdj =

αR

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Из условий леммы следует, что

òeiαz f (z)dz £ MαRR π (1- e−αR )® 0 ,

ΓR

при R ® ¥ .

Рассмотрим интегралы

+∞

ò eiαx R(x)dx ,

−∞

где

R(x) = Pm (x) . Qn (x)

В курсах математического анализа доказано, что интеграл существует, если Qn (x) ¹ 0 и n ³ m +1, можно записать

+∞		Pm (x)		s
ò	eiαx		dx = 2πi	выч	éeiαz R(z); z = z	ù .

		Q (x)		åIm zk >0	ë	k û
−∞		n		k=1

Выделяя действительную и мнимую части, получим

+∞

Pm (x)

cosαxdx = -2π Imç

выч

éeiαz R(z); z = z

ù ÷

;

Q (x)

åIm zk >0

û ÷

−∞

è k=1

+∞

Pm (x)

sinαxdx = 2π Reç

выч

éeiαz R(z); z = z

Q (x)

k û

−∞

è k=1

Замечание. Если α < 0 , можно использовать формулу

+∞

iαx

iαz

ò e

F(x)dx = -2πiå

выч

F(z); z = zk

ëe

û .

−∞

k =1

Im zk <0

+∞

(x -1)cos5x

Пример. Вычислить интеграл ò

dx .

- x + 5

−∞

(5.12)

(5.13)

Решение. Функция F(z) =

(z -1)e5iz

удовлетворяет условиям леммы Жордана, имеет в

- 2z + 5

верхней полуплоскости один плюс первого порядка z1 =1+ 2i . Найдем вычет

z -1

×e5iz ; z =1

+ 2i

(z -1) ×e5iz ö

выч

= ç

- 2z + 5

2z - 2

ë z

øz=1+2i

= 1 e−10

(cos5 + i sin5).

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

В оптике часто применяются интегралы Френеля òcos x2dx, òsin x2dx . Для вычисления

0 0

этих интегралов можно применить теорию функций комплексной переменной, специально выбрав контур интегрирования.

Выберем контур интегрирования как показано на рис.5.3.

	γ2	G+
	GR	R
	GR
0	γ1	x
	Рис.5.3.
Для вычисления интеграла введем функцию		f (z) = eiαz2 . В области GR функция f(z)

является аналитической и непрерывной на границе области, по интегральной теореме Ко- ши ò f (z)dz = 0 , где G = γ1 + G+R + γ2 . По свойствам интегралов можно записать равенство

Γ
R
ò f (x)dx + ò f (z)dz + ò f (z)dz = 0 .			(5.14)
0	γ2	Γ+R

Оценим интеграл

по

GR ,

где

GR : z = Reiϕ , 0 £ j £

. При z ÎGR , получим

eiz2

= e−R2 sin 2ϕ £ e−

4R2

ϕ , т.к. sin 2j ³

j при 0 £ j £

. Следовательно,

4R2ϕ

π / 4

(1- e−R2 )® 0, R ® ¥ .

ò f (z)dz

£ R ò e−

dj =

Γ+R

πi

πi R

Интеграл по γ2 ; z = t ×e

,0 £ t £ R, ò f (z)dz = -e 4 òe−t2 dt .

γ 2

Переходя в равенстве (3.23) к пределу при R → ∞ , получим

∞

πi ∞

òeix2 dx = e

òe−t2 dt .

∞

Известно, что òe−t2 dt =

(интеграл Пуассона), поэтому

∞

2π

òcos x2dx = òsin x2dx =

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Задачи для самостоятельного решения

5.4. Вычислить интегралы

2π

dϕ

а)

;

2 + sin ϕ

2π

sin2 ϕdϕ

г)

;

5 + 4cosϕ

+∞

ж) ò

dx ;

−∞

+∞

eix (x − 3)

м)

− 6x +109

−∞

∞

cos 2xdx

п)

;

0 (x2 + 4)

dϕ

cos4

б)

;

в)

dϕ ;

+12sin ϕ

+ sin

−π

0 1

2π

dϕ

+∞

x2dx

д)

ò0

;

е)

−∞ò

;

(6 + 5cosϕ)2

(x2 +1)(x2 + 9)

+∞

x2dx

+∞

(x −1)sin x

к) ò

;

л)

dx ;

−

2x + 2

−∞

+∞

x3 sin x

+∞ xsin x

dx ; н) ò

dx ;

о) ò

dx ;

+ 5x

+ 4

−∞

+∞

(x −1)cos 2x

р)

dx .

− 4x +

−∞

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1411 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.11.20196.78 Mб5Stroenie_veschestva_Laboratornye_raboty.doc
#
11.11.201880.38 Кб30Sushestvitelnoe-_rod_chislo.doc
#
03.12.2018645.63 Кб4Tablitsy.doc
#
05.06.2015361.98 Кб6tatwords.doc
#
19.04.2019262.84 Кб10Teoria_veroyatnostey_2.docx
#
05.06.2015611.32 Кб61TERECSHENKO.pdf
#
23.09.2019107.52 Кб12test1.doc
#
05.06.20151.22 Mб103Testy_k_ekzamenu.doc
#
16.11.2019458.24 Кб3topograficheskie_znaki (1).doc
#
26.11.201981.41 Кб3Trite metaphors.doc
#
25.11.20195.02 Mб59Uchebno-metodicheskoe_posobie_po_kursu_laborato...doc