
shpargalka_po_Difuram
.pdf
1.Дифференциальные уравнения.
Обыкновенным дифференциальным уравнением 1 порядка называется уравнение вида
F(x, y, y') 0 ,связывающее независимую переменную x, искомую функцию y f (x) и её производную y'(x) . При изложении
теории дифференциальных уравнений чаще всего рассматриваются уравнения, разрешенные относительно производной y'(x) :
y' f (x, y) или уравнения в так называемой симметричной форме:
Р(x, y)dx Q(x, y)dy 0
Частным решением дифференциального уравнения называется любая функция y (x) , которая, будучи подставленной
вместе со своей производной в уравнение, обращает его в тождество F x, (x), '(x) 0. Любое
дифференциальное уравнение имеет бесчисленное множество решений. Множество всех частных решений дифференциального уравнения называется его общим решением. Общее решение дифференциального уравнения 1 порядка является функцией,
зависящей от одной произвольной постоянной y (x, c).
Если решение найдено в неявной форме (x, y) c, то его называют общим интегралом дифференциального уравнения.
2.Уравнения с разделяющимися переменными.
Дифференциальное уравнение 1 порядка y' f (x, y) называется уравнением с разделяющимися переменными, если его правая часть есть произведение функций, одна из которых зависит от
переменной x , другая – от y: y' f1(x) f 2 ( y).
Уравнение, записанное в симметричной форме
Р(x, y)dx Q(x, y)dy 0 является уравнением с разделяющимися переменными, если множители P(x, y) и
Q(x, y) представляют собой произведение функций, из которых
одна зависит только от переменной x , другая – от переменной y :
1(x) 2 ( y) dx 1(x) 2 ( y) dy 0
Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал.
Вид уравнения: 1 1 + 2 2 = 0. Решение уравнения: приводим к уравнению с разделенными переменными ( + = 0) путем деления общих
частей уравнения на 1 |
2 (предполагая что 1 |
≠ |
|||||||||||
0; 2 |
≠ 0 ): |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
+ |
2 |
|
= 0 |
|
|||
|
|
|
2 |
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
= − |
1 |
+ |
|
||||||
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
|||||
В частности, уравнение вида ′ = |
( ) приводим к |
||||||||||||
уравнению + = 0 делением обеих частей на N(y):
|
|
= |
|
= |
|
|
|
= + . |
|||||||
|
|
|
|
|
|
||||||||||
Пример. 1 + 2 |
− |
1 − 2 = 0. |
|
|
|
|
|
||||||||
Решение: разделим обе части ур-ния на (1 + 2). |
|||||||||||||||
|
|
|
1 − 2 |
|
|
|
|
1 + 2 − 2 2 |
|
|
|
||||
|
|
= |
|
|
|
|
= |
|
= |
|
|
||||
|
|
1 + 2 |
|
1 + 2 |
|
||||||||||
1 2
=− 1 + 2
|
|
= |
1 |
− |
2 |
ln |
|
|
|
||||
|
|
1 + 2 |
= | − ln 1 + 2 + ln | |
Потенцируя, найдем общее решение в виде = 1+ 2
3. Уравнения, приводящие к уравнениям с разделяющимися
переменными.
Многие дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. К числу таких уравнений относятся, например, уравнения вида
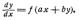 где а и Ь — постоянные величины, которые заменой переменных z — ах+by преобразуются в уравнения с разделяющими переменными. Действительно, переходя к новым переменным х и z, будем иметь
где а и Ь — постоянные величины, которые заменой переменных z — ах+by преобразуются в уравнения с разделяющими переменными. Действительно, переходя к новым переменным х и z, будем иметь
 или
или
И переменные разделились. Интегрируя, получим
Пример. |
Полагая z=2x+y будем иметь |
Разделяя переменные получим и интегрируя получим
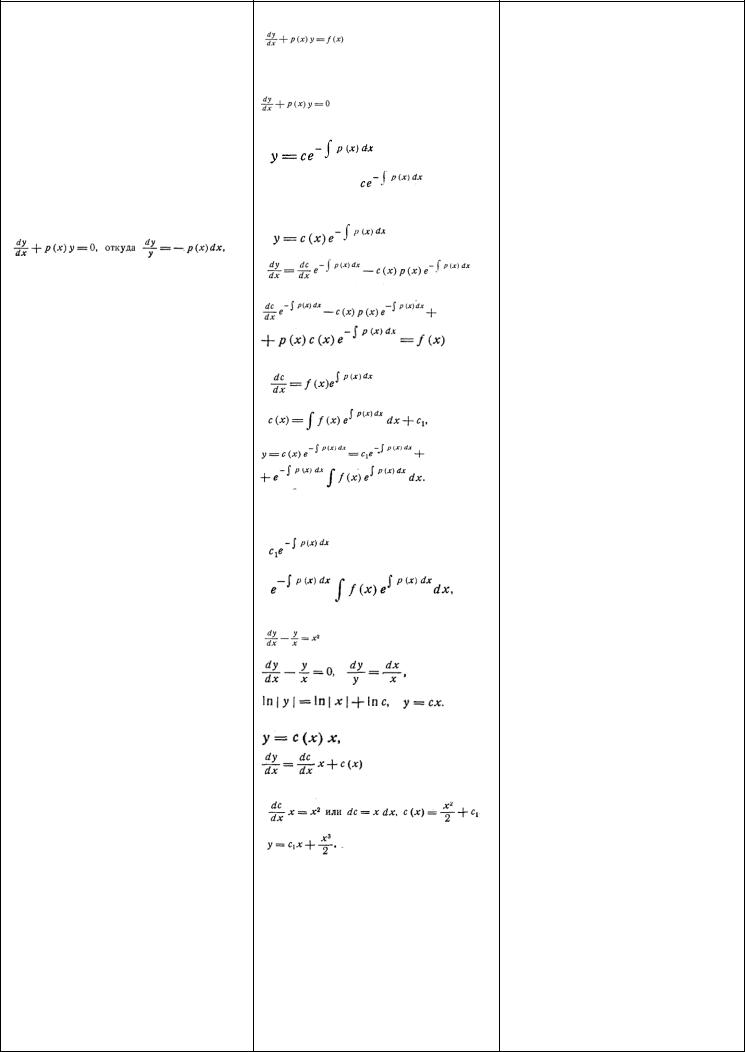
К уравнен. с разделяющимися переменными приводятся и так называемые однородные дифференциальные урав-ния 1 порядка
имеющие вид 
4. Линейные дифференциальные уравнения 1 порядка. Линейным дифференциальным уравнением порядка называется уравнение, линейное относительно функции и её производной:
y'P( x )y Q x - уравнение, линейное относительно y x ;
x' P( y )x Q y - уравнение, линейное относительно x y .
Здесь P x , Q y - заданные функции или константы. При
Q 0 уравнение называется однородным, при Q 0 -
неоднородным.
Однородные линейные уравнения (Q=0) могут быть решены разделением переменных. Неоднородные линейные уравнения можно свести к последовательности двух уравнений с разделяющимися переменными подстановкой
y u( x ) v( x ),
yu' x v x u x v' x .
Влинейном однородном уравнении переменные разделяются:
И интегрируя получаем
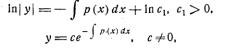 (2)
(2)
При делении на у мы потеряли решение у≡ 0, однако оно может быть включено в найденное семейство решений (2), если считать что с может принимать значение 0.
5. Уравнения 1 порядка. Метод вариации произвольной постоянной.
Для интегрирования неоднородного линейного уравнения
Может быть применен так называемый метод вариации постоянной При применении этого метода сначала интегрируется
соответствующее однородное уравнение
Общее решение которого имеет вид
При постоянном с, функция является решением однородного уравнения. Попробуем теперь удовлетворить неоднородному уравнению, считая с функцией х, т.е.по существу совершая замену переменных
Где с(х) – новая неизвестная функция х. Вычисляя производную
И подставляя в исходное неоднородное уравнение получим
Или
Откуда интегрируя находим
А следовательно
(*)
Итак общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения.
и частного решения неоднородного уравнения
получающегося из (*) при с1=0. Пример
Интегрируем соответствующее однородное уравнение
Считаем с функцией х, тогда
И подставляя в исходное уравнение после упрощения получаем
Следовательно общее решение
6. Уравнение 1 порядка.Метод Бернулли
Вид уравнения: ′ + = |
|
+ = ,( ) где |
|
|
|
|
|
( ), ( ) – непрерывные функции или постоянные. |
|||
Решение уравнения: метод Бернулли. Решение будем искать в |
|||
виде = ( ), тогда ′ |
= ′ + ′ . Подставляя в |
||
уравнение получаем ′ + ′ |
+ = ′ + |
||
′ + = . (1).Функцию ( ) будем искать, как частное
решение дифф. урав-ния ′ + = 0. Тогда |
= − |
( ) . |
||
Подставляя в уравнение (1), имеем = |
|
|
+ . |
|
|
||||
Таким образом, общее решение линейного уравнения ( ) имеет вид: = = ( + ) − ( ) .

7. Уравнение Бернулли
Решение осуществляется методом Бернулли или сведением к линейному, путем замены переменных. Например, уравнение Бернулли имеющее вид
Или
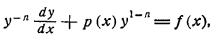 (*)
(*)
Заменой переменных  сводится к линейному
сводится к линейному
уравнению. Действительно, дифференцируя 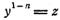 находим
находим
И, подставляя в (*) получим линейное уравнение
Пример.
и т.д.
8. Уравнения в полных дифференциалах
Вид уравнения: , + , = 0, где функции
P , |
и Q , удовлетворяют условию: |
|
||||||||||
|
|
= |
|
. Левая часть этого уравнения – полный |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||
дифференциал некоторой функции , , т.е. |
|
|||||||||||
= 0 |
, |
= . Причем ′ |
= ( , ) , ′ |
= |
||||||||
( , ). |
|
|
|
|
|
|
||||||
|
|
= , |
= |
, + . Для нахождения |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
+ ′ |
|
|||
, найдем ′ = |
, ′ |
|
||||||||||
′ = , − ( |
( , ) )′ + ′ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
= |
, − ( ( , ) )′ |
|
||||||||||
= |
|
, + |
, − ( |
( , ) )′ |
= |
|||||||
Пример: |
|
|
|
|
|
|
||||||
+ + + + + = 0 |
|
|||||||||||
|
= 1 + = |
|
= 1 + |
|
|
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|||||||||
= |
+ |
= |
( + + ) + ( ) = |
|||||||||
|
|
|
|
|
|
|
|
|
+ + + ( ) |
|
||
|
= + + |
′ = , = + + |
||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
′ =
=
, = + + + = .
9. Интегрирующий множитель
Рассмотрим уравнение , + , = 0 . (1) если ≠ , то иногда удается подобрать такую
функцию , , после умножения на которую всех членов уравнения левая часть уравнения становится полным дифференциалом, общее решение которого совпадает с общим решением первоначального
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Функция , |
называется интегрирующим |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
множителем ур.(1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Инт.мн-ль легко находится в след.случаях: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= Φ , тогда |
= Φ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Ψ , тогда |
= |
Ψ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + − = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
, = |
|
2 |
+ ; , = −; |
|
= 1; |
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
−1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
= |
−1 − 1 |
|
= Ψ , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 + 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= − |
|
|
= Φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Найдем = |
|
Ψ = (−2) = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
−2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
= |
|
|
2 |
|
= полагая С = 1 = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Домножим первоначальное уравнение на |
1 |
: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
2 + − |
1 |
|
= 0 1 + |
|
|
|
− |
|
1 |
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= 0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Получили уравнение в полных дифференциалах, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
где |
|
|
= 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Интегрируем |
|
|
|
= 1 + |
|
по : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
= |
1 + |
|
|
|
|
+ = − |
+ |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Дифференцируем это равенство по y: |
|
= − |
1 |
+ |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
′ |
|
. Но по условию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
= − |
1 |
. Приравняем правые части этих |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
выражений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
− |
1 |
|
+ ′ |
= − |
1 |
|
′ |
|
= 0 ′ |
|
|
= . Тогда |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
общий интеграл уравнения будет иметь вид: |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
− |
|
|
= , а общее решение = 2 − . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||

10. Дифференциальные уравнение высших порядков. Общие сведения
Диф.уравнения n порядка имеют вид
( ) = ( , , ′ , … , (−1)), или если они не разрешены относительно старшей производной, , , ′ , … , = 0.
Теорема.Существует единственное решение дифференц. уравнения n порядка ( ) = ( , , ′ , … , ( −1)), удовлетворяющее условиям
0 = 0; ′ 0 = 0′ ; … ; −1 0 = 0( −1), если в окрестности начальных значений ( 0, 0, ′ 0, … , 0 −1 ) функция f является непрерывной функцией всех своих аргументов и удовлетворяет условию Липшица(существует число q, 0<= q < 1 такое, что P(F(x), F(y))<= qP(x, y) для всех x, y принадл. X.) по всем аргументам, начиная со второго. Общим решением дифф.уравнения n порядка называется множество решений, состоящее из всех без исключения частных решений. Если правая часть уравнения в некоторой области изменения аргументов удовлетв.условиям теоремы, то общ.решение зависит от n параметров, в качестве которых могут быть выбраны, например начальные значения искомой функции и ее производных.
11. Уравнения, допускающие понижение порядка.
′′ = |
2 |
= |
Решение сводится к |
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
двукратному интегрированию. |
|
|
|
|
|
|
|||||||||||||
Пример. ′′ = 2 |
2 |
|
= 2 ′ = − |
2 |
+ |
|
|||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||
1 = − |
+ 1 + 2. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
′′ = , ′ |
2 |
= |
, |
|
(явно не содержит |
|
|
||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y).При решении применяется замена |
|
= |
|
|
= |
|
. |
||||||||||||
|
|
2 |
|
||||||||||||||||
Подставляя в исходное уравнение, получаем уравнение 1 порядка = ( , ). Решив его находим = ( , 1)
Так как = |
|
, получаем общий интеграл исходного |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
уравнения: |
|
|
|
|
|
|
|||
= |
, 1 + 2 |
|
|
|
|
||||
′′ |
= , ′ |
|
2 |
= |
, |
|
(явно не содержит |
||
2 |
|
||||||||
x).При решении применяется замена |
|
= (p – функция |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
от y) |
|
= |
|
|
|
|
= |
|
|
|
|
= |
|
. Подставляя в исходное |
||||||||||||||||||||||
2 |
|
|
|
|||||||||||||||||||||||||||||||||
получаем |
|
|
= ( , ) - уравнение 1 порядка. Решая, |
|||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
найдем = , 1 |
. Т.к. = |
|
,то |
|
= , 1 |
. Разделяя |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
переменные, находим общий интеграл исходного |
||||||||||||||||||||||||||||||||||||
уравнения Φ , , 1, 2 |
|
= 0. |
(′)2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Пример. ′′ |
|
= (′)2 . ′′ |
= |
|
= |
|
′′ = |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
ln = ln + = |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ln( 1 ) = 1 . Возвращаясь к замене имеем: |
||||||||||||||||||||||||||||||||||||
= |
|
|
= |
|
= |
ln = + |
||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
||||
= 1 + 2 = 2 1
14. Линейные дифференциальные уравнения высших порядков
Лин.Диф.Ур-нием n порядка называется уравнение линейное относительно неизвестной функции и ее производных и, следовательно, имеющее вид:
|
+ −1 |
+ + |
′ + = |
0 |
1 |
−1 |
|
. (1) |
|
|
|
Если правая часть |
≡ 0, то уравнение называется |
||
линейным однородным, т.к.оно однородно относительно неизвестной ф-ии и ее производных.,иначе называется не однородным. Если
|
= то данное уравнение является |
|
|
|
|||||||||||
нестационарным, а если |
= то уравнение |
||||||||||||||
стационарное. |
|
|
|
|
|
|
|
|
|
|
|
||||
Т1. Если 1 |
и 2 есть решение диф.ура 0 ′′ |
+ 1 ′ + |
|||||||||||||
2 = 0. То 1 + 2 также является решением этого |
|||||||||||||||
этого ур-ния. 0 ′′ 1 |
+ ′′ |
2 |
+ 1 |
′ 1 |
+ ′ 2 |
+ |
|
|
|||||||
+ |
|
= ′′ |
1 |
+ ′ |
+ |
+ ′′ |
2 |
+ |
|||||||
2 |
1 |
2 |
|
0 |
|
1 |
1 |
|
2 |
1 |
|
0 |
|
||
|
′ |
+ |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Т2. Если 1 |
есть решение уравнения (1), то 1 также |
||||||||||||||
явл.решением данного ур-ния. |
|
|
|
|
|
|
|
||||||||
Замечание: Если 2 решения 1 и 2 |
можно определить |
||||||||||||||
как 1 |
= 2 |
то такие решения называются линейно |
|||||||||||||
зависимыми. 1 ≠ 2 –линейно не зависимыми. |
|||||||||||||||
Т3.Если 1 и 2 |
есть лин.зависимые решения ур-ния (1), |
|||||
то определитель Вронского =0. |
|
|
|
|||
1 |
2 |
1 |
1 |
1 |
1 |
|
= ′ |
′ = |
′ |
′ |
= ′ |
′ |
= 0 |
1 |
2 |
1 |
1 |
1 |
1 |
|
Т4. Если на каком либо отрезке , при начальных условиях 0, 0 ≠ 0 и определитель Вронского в этой точке ≠ 0, то во всех остальных точках отрезка опред-ль Вронского ≠ 0.
Т5. Если 1 и 2 есть лин.независимые частные решения ур-ния (1), то общее решение этого уравнения можно представить в виде: = 1 1 + 2 2.
1.это выражение явл-ся решением 2.это решение явл-ся общим решением.( = )

15. Линейные неоднородные дифференциальные уравнения высших порядков. Метод
Подбора
′′ = ′ + = ( )
Т.Общее решение лин.неоднородного ур-ния может быть представлено как сумма двух решений.
= + ( ) где -общее решение, -к- либо частное решение неоднородн.ур-ния.
Пусть 1, 2 есть решения соответств. однородного ур-ния:
= 1 1 + 2 2
′′ + ′′ + ′ + ′ + |
+ = |
′′ + ′ + + ′′ + ′ + = ( ) (скобка =0).
0 = 0
′ ( 0) = ′ 0
1 0 ; 2 0 ; ′1 0 ; ′2 0 ; 0 ; |
|
|
|
|||||||||||||||||
= |
+ |
+ ( ) |
|
|
|
|||||||||||||||
|
0 |
|
|
1 |
1 |
|
0 |
|
|
2 |
2 |
0 |
0 |
|
|
|
||||
′ |
0 |
= ′ |
|
|
+ ′ |
2 |
|
+ ′ ( ) |
|
|
|
|||||||||
|
|
|
1 |
1 |
|
0 |
|
|
2 |
|
0 |
0 |
|
|
|
|||||
|
|
|
+ |
|
= |
− |
|
|
|
|
||||||||||
|
1 |
|
1.0 |
|
|
|
2 |
2.0 |
|
0 |
|
|
0 |
|
|
|
|
|||
′ |
|
+ ′ |
|
|
= ′ |
|
− ′ - общее решение для любых |
|||||||||||||
1 |
1.0 |
|
|
|
|
2 |
|
2.0 |
|
|
0 |
|
0 |
|
|
|
|
|||
началных условий |
|
|
|
|
|
|
|
|
||||||||||||
Метод подбора. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= ( ) |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ( ) , ≠ 1,2 |
если не есть корень |
|
|
|||||||||||||||||
характеристического ур-ния |
|
|
|
|||||||||||||||||
′ = ′ |
|
|
|
+ ( ) |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
′′ |
= ′′ |
|
+ 2 ′ |
+ 2 ( ) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
′′ |
|
+ 2 ′ |
|
+ 2 + ′ |
|
+ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
= ( ) (сокращаем на ) |
||||||||||||||||||
′′ |
|
+ 2 + ′ |
+ 2 + + = |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если = 1 тогда = ( ) |
|
|
|
|||||||||||||||||
= 1 = 2=> = 2 ( ) |
|
|
|
|||||||||||||||||
Пример. ′′ |
− 4 ′ + 3 = 2 3 |
|
|
|
||||||||||||||||
2 − 4 + 3 = 0 |
|
|
|
|
|
|
|
|
|
|||||||||||
= 2 ± |
|
|
4 − 3 |
|
|
|
|
|
|
|
|
|
|
|||||||
1 = 3; |
|
2 = 1 |
|
|
|
|
|
|
|
|
|
|||||||||
= 1 3 + 2 -общ.решение.
= 2 + + 3
′ = 3 2 + 2 + 3 + 3( 3 + 2 2 + ) 3
′′ = |
6 + 2 3 + 6 3 2 + 2 + 3 + 9( 3 |
|
+ 2 + ) 3 |
6 + 2 + 18 2 + 12 + 6 + 9 3 + 9 2 + 9
−12 2 − 8 − 4 − 12 3
−12 2 − 12 + 3 3 + 3 2
+ 3 = 2
6 = 1 |
|
= 1/6 |
|
|
|
|||
6 + 4 = 0 => = −1/4 |
|
|
||||||
2 + 2 = 0 |
= 1/4 |
|
|
|
||||
|
|
3 |
2 |
|
|
|||
= 3 + + ( |
|
− |
|
+ |
|
) 3 |
||
|
|
|
||||||
1 |
2 |
6 |
|
4 |
|
4 |
|
|
|
|
|
|
|
||||
16. Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной
′′ + ′ + = ( )
= 1 1 + 2( ) 2
′ = ′1 1 + ′2 2 + 1′1 + 2′2
′1 1 + ′2 2 = 0
′ = 1′1 + 2′2
′′ = ′1′1 + ′2′2 + 1′′1 + 2′′2
′1′1 + ′2′2 + 1′′1 + 2′′2 + 1′1 + 2′2 + 1 1
|
|
|
|
|
|
+ 2 |
2 |
= ( ) |
|
|
||
|
′′ |
1 |
+ ′ |
1 |
+ |
+ ′′ |
2 |
+ ′ |
+ |
+ ′ ′ |
||
1 |
|
|
1 |
2 |
|
2 |
2 |
1 |
1 |
|||
|
|
|
|
|
|
+ ′2′2 |
= ( ) |
|
|
|||
′1 ′1 + ′2 ′2 = ( ) |
|
|
|
|
|
|
||||||
|
′ |
|
+ ′ |
2 |
= 0 |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
||
Пример.
′′ + =2 + 1 = 0
1,2 = ±
= 1 + 2
′ = −1 + 2
′′ = −1 − 2
|
′1 + ′2 = 0 |
|
|
|
|
|
||||||||||
−′ |
1 + ′ 2 = |
|
|
|
|
|
||||||||||
= |
|
|
|
|
|
= 2 + 2 = 1 |
|
|
|
|||||||
|
|
|
− |
|
|
|
|
|
|
|
||||||
|
|
= |
|
0 |
|
= − |
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
= |
|
|
0 |
= |
|
|
|
|
|
|||||
|
|
|
|
|
− |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
′1 = |
|
1 |
= − |
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|||||||||
′2 = |
|
|
= |
|
|
|
|
|
|
|||||||
|
|
|
1 + |
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
= − |
|
|
= = − |
2 |
|
+ |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
1 − |
|
1 |
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
= − |
|
+ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
|
|
|
= − + |
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
…
= − ln 1 + sinx + 1 cosx + 2 sinx cosx
17. Уравнение Эйлера
0 ( ) + 1 −1 (−1) + + −1 ′ + = ( )
где все −постоянные, называются уравнениями Эйлера. Ур-ние Эйлера заменой независимого переменного x= (t=lnx; y(x)=y(x(t)))преобразуется в линейное однородное уравнение с постоянными коэффициентами.
Линейно входящие в ур-ние Эйл. |
|
|
|
|
|
|
|
= 0 с |
|||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
=0 |
|
− |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
постоянными коэфф.произведения |
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
+ |
2 |
+ + |
|
линейно |
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
1 |
2 2 |
|
|
|
|
|
|
|
|
|
||||
выражаются через производные функции у по новой независимой переменной t. Отсюда => что преобразованное ур-ние будет линейным однородным ур-нием с постоянными коэффициентами.
Пример. 2 ′′ |
− 3 ′ + 4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
= |
|
= |
|
|
|
|
= |
|
|
′ |
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
2 |
+ |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
2 |
+ |
|
− |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
2 |
+ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
− |
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
2 |
− |
|
|
−2 |
− 3 |
|
|
− − 4 = 0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
− |
|
|
|
− 3 |
|
+ 4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
− 4 |
|
+ 4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 − 4 + 4 = 0
1,2 = 2
= 1 2 + 2 2
= 1 2 + 2 2
Если уравнение не однородное то переменную x на заменяют как в левой так и в правой частях.
Если уравнение более высокого порядка, чем 2 то замена ( ) на ( ) происходит по аналогичной схеме.

13. Уравнение Клеро
= ′ + ( ) Дифференцируя по получим: = +
+ ′ ; или
( + ′ ) =0; откуда или =0 и, значит, = , или+ ′ = 0. В первом случае, исключая получим: =
+ ( ) - однопараметрическое семейство интегральных прямых (общее решение). Во втором случае решение определяется уравнениями = + ( ) и + ′ = 0.
Интегральная кривая определяемая данными уравнениями является огибающей семейства интегральных прямых.(т.е. огибающая некоторого семейства
Φ , , = 0 определяется уравнениями Φ , , = 0 и Φ = 0; которые для семейства = + ( )
имеют вид = + ( ) и + ′ = 0 и от тех уравнений отличается лишь обозначением параметра (с вместо p))
Особое решение. Необходимо исключить параметр . Соотношение Φ , = 0 определяет дискриминантную кривую, касательными к которой будет общие решения (по отношению к ним дискриминантная кривая - огибающая).
Пример. = ′ + |
( ′ )2 |
; = + |
2 |
, где = |
2 |
; |
|||||||
|
2 |
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
Общее: = + |
-семейство прямых, |
|
|
||||||||||
2 |
|
|
|||||||||||
|
= −′ |
|
= − |
|
|
||||||||
|
|
|
|
||||||||||
Особое решение: |
= − + |
2 |
= − |
2 |
|
|
|||||||
|
2 |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Исключая параметр : = − |
2 |
- огибающая для |
|
|
|||||||||
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
семейства прямых.
18. Общее понятие разностных уравнений
В качестве аналогов дифф.уров можно рассм. разностные ур-ния. При использовании обратных
разностей линейные неоднородные разностные уравнения имеют вид: 0 m y n + 1 m−1y n + +
y n = f n , где f[n] –заданная, а y[n] –искомая решетчатые ф-ции. При f n ≡ 0 уравнение становится однородным. Другой вид разн. ур-ния 0 +
1 − 1 + + − = .
Это разностное ур-ние можно рассматривать как рекуррентное отношение позволяющее вычислять значения y[n+ для любых n по известному значению функции в правой части уравнения и начальным условиям y[n-1+,…y[n-m+. Такие вычисления легко выполняются на счетных машинах, а также не представляют никаких принципиальных трудностей и при ручном счете, даже в тех случаях кошда коэффициенты в левой части уравнения меняются по времени. Это отличает разностные уравнения от непрерывных аналогов – дифф.уров.
Общее решение однородного разностного уравнения при некратных корнях характеристичесого уравнения может быть записано след.образом
|
|
|
|
= 1 1 |
+ 2 2 |
+ … + где -корни |
характеристического уравнения 0 + 1 −1 + += 0. а -произвольные постоянные.
19. Решетчатые функции
Введем понятие решетчатой функции времени f[nT+ или в сокр.записи f[n+. Значения которой определены в дискретные моменты времени t=nT, где n- целое число, а T-период повторения. Операция замены непрерывной функции решетчатой, представлена в след виде.(см рис.) Решетчатая ф-ция не обязательно должна формироваться из некоторой исходной непрерывной функции. Любая числовая посл-ть некоторой величины, определенной в дискретные равноотстоящие моменты времени, может трактоваться как решетчатая функция. Обратная задача – формирование непрерывной функции из решетчатой – не может быть решена однозначно, т.к. ф-ции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций. Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.
Прямая и обратная разности. Аналогом первой производной непрерывной функции для решетчатой функции является либо первая прямая разность ∆ = + 1 − , либо первая обратная разность
= − − 1 . Прямая разность определяется в момент времени t=nT по будущему значению решетчатой функции при t=(n+1)T. Это можно сделать в тех случаях, когда будущее значение известно, либо, если это будущее значение нужно вычислить. Обратная разность определяется для момента времени t=nT по прошлому значению решетчатой функции в момент времени (n-1)T. Важная особенность обратных разностей. Если решетчатая ф-ция определена только для положительных значений аргумента, т.е. f[n]≡ 0 при n<0 то в точке n=0
kf 0 = f[0] для положительного k.

20. Конечные разности элементарных функций
f(n)=bn+a
∆f(n)=b(n+1)+a-b(n)-a=b ∆2f(n)=∆f(n+1)-∆f(n)=0
f(n)=n2+bn+c ∆f(n)=(n+1)2+b(n+1)+c-n2-bn-c=2n+b+1 ∆2f(n)=2(n+1)+b+1-2n-b-1=2
∆3f(n)=0
f(n)=ean ∆f(n)=ea(n+1)-ean=ean(ea-1)
∆2f(n)=ea(n+1)(ea-1)-ean(ea-1)=ean(ea-1)2 ∆kf(n)=ean(ea-1)k
21. Разностные уравнения. Линейные разностные уравнения.
— уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, ..., xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени. Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность
y = y(t+1) – y(t),
которую часто называют первой разностью. При этом различают правую и левую разности, в частности
y = y(t) – y(t–1)
— левая, а приведенная выше — правая. Можно определить вторую разность:
Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) –
– 2y(t + 1) + y(t)
и разности высших порядков Δn.
Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке:
f [y(t), y(t), ..., ny(t)] = 0.
Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек y(t), y(t+1), ..., y(t+n).
При этом разность между последним и первым моментами времени называется порядком уравнения. При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю.
При исследовании функций многих переменных по аналогии с частными производными (см. Производная) вводятся также частные разности.
Линейные разностные уравнения первого порядка y(x + 1) − ay(x) = 0. Линейное однородное разностное уравнение первого порядка с постоянными коэффициентами.
y(x + 1) − ay(x) = f(x). Линейное неоднородное разностное уравнение первого порядка с постоянными коэффициентами.
y(x + 1) − xy(x) = 0.
y(x + 1) − a(x − b)(x − c)y(x) = 0.
y(x + 1) − R(x)y(x) = 0, где R(x) -- рациональная функция. y(x + 1) − f(x)y(x) = 0.
y(x + a) − by(x) = 0. y(x + a) − by(x) = f(x). y(x + a) − bxy(x) = 0. y(x + a) − f(x)y(x) = 0.
Линейные разностные уравнения второго порядка, yn
= y(n)
yn+2 + ayn+1 + byn = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.
yn+2 + ayn+1 + byn = fn. Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.
y(x + 2) + ay(x + 1) + by(x) = 0. Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами.
y(x + 2) + ay(x + 1) + by(x) = f(x). Линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами.
y(x + 2) + a(x + 1)y(x + 1) + bx(x + 1)y(x) = 0.
23. Линейные стационарные неоднородные разностные уравнения Метод подбора. Методом Лагранжа может быть решено любое неоднородное
уравнение с постоянными коэффициентами. Однако если свободный член в уравнении
имеет вид
(37)
где Pm1(x) и Qm2(x) - многочлены степеней, соответственно, m1 и m2, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и
тригонометрических функциях число 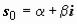 и пусть r - кратность числа s0 как корня характеристического уравнения, m = max(m1, m2). Тогда частное решение надо искать в виде
и пусть r - кратность числа s0 как корня характеристического уравнения, m = max(m1, m2). Тогда частное решение надо искать в виде
 где Rm(x) и Sm(x) - многочлены степени m с неопределёнными коэффициентами. Дифференцируя функцию yчн n раз, подставив эти производные в уравнение и приравнивая коэффициенты при одинаковых степенях x и одинаковых тригонометрических функциях (sin x или cos x), получим систему из 2(m + 1) уравнений относительно 2(m + 1) неопределённых коэффициентов многочленов Rm(x) и Sm(x). Решив эту систему, определим коэффициенты функции yчн(x).
где Rm(x) и Sm(x) - многочлены степени m с неопределёнными коэффициентами. Дифференцируя функцию yчн n раз, подставив эти производные в уравнение и приравнивая коэффициенты при одинаковых степенях x и одинаковых тригонометрических функциях (sin x или cos x), получим систему из 2(m + 1) уравнений относительно 2(m + 1) неопределённых коэффициентов многочленов Rm(x) и Sm(x). Решив эту систему, определим коэффициенты функции yчн(x).
Технику работы с этим правилом будем осваивать, начиная с простейших случаев, при этом будем формулировать частные правила, вытекающие из общего.
I. Если f(x) = Pm(x) (т.е. f(x) - многочлен степени m), то частное решение ищется в виде yчн(x)= Rm(x), если число 0 не является корнем характеристического уравнения, и в виде yчн(x)= xr Rm(x), если число 0 - корень характеристического уравнения кратности r. Rm(x) - многочлен степени m с неопределёнными коэффициентами.
Это правило следует из общего, если записать f(x) = Pm(x)
в виде f(x) = e0 x [Pm(x) cos 0x + 0 sin 0x+. В этом случае s0 = 0 + 0i, m1 = m, m2 = 0, max(m1, m2) = m, поэтому
yчн(x)= xr e0 x [Rm(x) cos 0x + Sm(x) sin 0x] = xr Rm(x) .
Примеры: 1. Найти общее решение уравнения
Решение: характеристическое уравнение k2 - 5 k + 6 = 0, его корни k1 = 2, k2 = 3, yoo = C1e 2x + C3e 3x. Степень многочлена m = 3, число 0 не является корнем
характеристического уравнения (r = 0), поэтому yчн(x) ищем в виде многочлена третьей степени с неопределёнными коэффициентами: yчн(x)= xr Rm(x) = Ax3
+ Bx2 + Dx + E. Тогда
подстановка этих выражений в уравнение даст *6Ax + 2B+
- 5[3Ax2 + 2Bx + D] + 6[Ax3 + Bx2 + Dx + E] = x3 - 2x.
Приводим подобные члены: 6Ax3 + [-15A + 6B] x2 + [6A - 10B + 6D] x + [2B -5D + 6E] = x3 - 2x. Сравниваем коэффициенты при одинаковых степенях x:
x3 |
6A = 1; |
|
A = 1/6; |
x2 |
- 15A + |
6B =0; |
B = 15A/6 = |
5/12; |
|
|
|
x |
6A – 10B + 6D = -2; |
D = 5B/3 – A – |
|
1/3 = (25 – 6 – 12)/36 = 7/36; |
|
||
1 |
2B |
– 5D + 6E = 0; |
E = 5D/6 – |
B/3 = 35/216 – 5/36 =(35 – 30)/216 = 5/216.
Итак,

24. Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных.
Общее решение линейного уравнения с правой частью получается из общего решения соответствующего уравнения без правой части с помощью квадратур. Для этого можно применить следующий прием.
В общем решении уравнения без правой части заменяем все произвольные постоянные неизвестными функциями. Полученное выражение дифференцируем и попутно подчиняем неизвестные функции добавочным условиям, упрощающим вид последовательных производных. Подставляя выражение производных y’, y’’, y’’’ и т.д. в данное уравнение, получаем еще одно условие, налагаемое на неизвестные функции. Тогда оказывается возможным найти первые производные всех неизвестных функций и остается выполнить квадратуры.
Этот метод применим к линейным уравнениям любого порядка как с постоянными, так и с переменными коэффициентами. Рассмотрим уравнение второго порядка: y’’+P(x)y’+Q(x)=R(x) (1)
Пусть общее решение соответствующего уравнения без правой части есть
y=C1f1(x)+C2f2(x). (2)
Ищем общее решения уравнения (1) в виде (2), считая теперь C1 и С2 неизвестными функциями от х. Дифференцируя (2), находим:
y’=C1f1’(x)+C2f2’(x)+ C1’f1(x)+C2’f2(x) |
(3) |
Вводим добавочное условие |
|
C1’f1(x)+C2’f2(x)=0. |
(4) |
Тогда вид первой производной упрощается, и мы имеем:
y’= C1f1’(x)+C2f2’(x). |
(5) |
|
Дифференцируя еще раз имеем: |
|
|
y’’= C1f1’’(x)+C2f2’’(x)+ C1’f1’(x)+C2’f2’(x) |
(6) |
|
После подстановки выражений (2), (5) и (6) в уравнение (1) все члены, содержащие С1, взаимно уничтожатся (ибо функция y=f1(x) есть решение уравнения y’’+Py’+Qy=0); точно так же взаимно уничтожатся все члены, содержащие С2, и мы получим еще одно условие
C1’f1’(x)+C2’f2’(x)=R(x) |
(7) |
Условия (4) и (7) позволяют найти выражения производных С1’, C2’ и остается выполнить квадратуры.
25. Общие сведения о линейных системах.
Системой дифференциальных уравнений называется совокупность уравнений, содержащих несколько неизвестных функций и их производные, причем в каждое из уравнений входит хотя бы одна производная. На практике имеют дело с такими системами, где число уравнений равно числу неизвестных.
Система называется линейной, если неизвестные функции и их производные входят в каждое из уравнений только в первой степени. Линейная система имеет нормальный вид, когда она решена относительно всех производных.
26. Метод сведения линейной системы к одному уравнению.
Пример 1. Система дифференциальных уравнений
|
|
|
= − + 23 2 |
1 |
|
|
|
||
|
= −4 − 2 + 4 + 1 |
(2) |
||
|
|
|||
-линейная; она имеет нормальный вид.
вэтом примере мы имеем линейную систему с постоянными коэффициентами (коэффициенты при неизвестных функциях и их производных постоянны).
Из линейной системы (присоединяя к ней уравнения, выведенные дифференцированием) можно исключить все неизвестные (и их производные), кроме одной. Полученное уравнение будет содержать одну неизвестную функцию и ее производную первого и более высоких порядков. Это уравнение тоже будет линейным, а если исходная система была системой с постоянными коэффициентами, то и найденное уравнение высшего порядка будет иметь постоянные коэффициенты.
Разыскав неизвестную функцию этого уравнения, подставляем ее выражение в данные уравнения и находим остальные неизвестные функции.
Пример 2. Решить линейную систему
примера 1.
Решение: Чтобы исключить y и , продифференцируем (1). Получим:
2 |
|
= |
|
- |
|
+ 3t. |
(3) |
|
|
2 |
|
|
|||||
|
|
|
|
Из уравнения (1) находим выражение y через t, x и ;
подставляя в (2), найдем выражение через те же
величины. Подставляя это выражение в (3), получим линейное уравнение второго порядка
2 |
|
|
|
2 |
|
|
2 |
+ |
|
- 6х=3t -t-1 |
(4) |
|
|
||||
Находим его общее решение |
|
||||
x=C1e2t+C2e-3t - 21t2 |
(5) |
||||
Это выражение подставляем в уравнение (1) и находим вторую неизвестную функцию
y = - |
|
+ x + 23t2 = - C1e2t + 4C2e-3t + t2 + t |
(6) |
|

27. Системы дифференциальных уравнений с постоянными коэффициентами
В векторной форме:
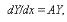 где
где
Характеристическое уравнение
Или Нахождение общего решения системы по методу Эйлера
Если - простой корень характеристического уравнения, то ему соответствует решение
2. Если - корень кратности m характеристического уравнения, то ему соответствует решение вида
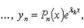 где P1(x), P2(x), ..., Pn(x) - многочлены степени не выше m-1, имеющие в совокупности m произвольных постоянных.
где P1(x), P2(x), ..., Pn(x) - многочлены степени не выше m-1, имеющие в совокупности m произвольных постоянных.
Коэффициенты многочленов можно определить, подставив выражения для y1, y2, ..., yn в исходную систему. Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений. Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням , будут:
то
общее решение этой системы имеет вид:
Линейная неоднородная система диф ур с постоянными
коэфф.  где Общее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы
где Общее решение неоднородной системы есть сумма общего решения однородной системы и некоторого частного решения неоднородной системы. Для нахождения общего решения неоднородной системы
можно применить метод Лагранжа вариации произвольных постоянных.
28. Решение дифференциальных уравнений с использованием преобразования Лапласса
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так линейные дифференциальные уравнения становятся алгебраическими.
Решение.Находим изображения правых и левых частей уравнения
Решив систему, получим
Разложим каждую дробь на простые дроби вида
Для |
получаем систему |
Откуда
Для |
получаем систему |
Откуда
Для |
получаем систему |
Откуда
Ответ:
1.Дифференциальные уравнения.
2.Уравнения с разделяющимися переменными.
3.Уравнения, приводящие к уравнениям с разделяющимися переменными.
4.Линейные дифференциальные уравнения 1 порядка.
5.Уравнения 1 порядка. Метод вариации произвольной постоянной.
6.Уравнение 1 порядка.Метод Бернулли
7.Уравнение Бернулли
8.Уравнения в полных дифференциалах
9.Интегрирующий множитель
10.Дифференциальные уравнение высших порядков. Общие сведения
11.Уравнения, допускающие понижение порядка.
13.Уравнение Клеро
14.Линейные дифференциальные уравнения высших порядков
15.Линейные неоднородные дифференциальные уравнения высших порядков. Метод Подбора
16.Линейные неоднородные дифференциальные уравнения высших порядков. Метод вариации произвольной постоянной
17.Уравнение Эйлера
18.Общее понятие разностных уравнений
19.Решетчатые функции
20.Конечные разности элементарных функций
21.Разностные уравнения. Линейные разностные уравнения.
23.Линейные стационарные неоднородные разностные уравнения Метод подбора.
24.Линейные стационарные неоднородные разностные уравнения. Метод вариации произвольных постоянных.
25.Общие сведения о линейных системах.
26.Метод сведения линейной системы к одному уравнению.
27.Системы дифференциальных уравнений с постоянными коэффициентами
28.Решение дифференциальных уравнений с использованием преобразования Лапласса
