Сверхпроводниковый квантовый интерферометр Джозефсона (сквид)

СКВИД (на английском –SQUID–SuperonductingQUantumInterferenceDevice) – сверхчувствительный магнетометр, один из наиболее распространенных сверхпроводниковых приборов. Рассмотрим, так называемый, двухплечевой СКВИД, представляющий собой сверхпроводящую петлю с входным и выходным токовыми контактами, в которую вставлены два джозефсоновских перехода (контакта)aиb.

Подобно тому, как мы это делали при выводе формулы для квантования магнитного потока в сверхпроводящей полости, рассмотрим разрывный контур C`, который находится в объеме материала сверхпроводящего кольца на расстоянии от поверхности большем, чем глубина проникновения магнитного поля, и имеет точки разрыва на берегах туннельных контактов толщиной δ. Ток на контуре, при этом равен нулю. На туннельных контактах фаза испытывает скачки и член с градиентом фазы в выражении для тока не определен:

Проинтегрируем на контуре C`выражение для тока. Поскольку вектор-потенциал – гладкая функция и длина δ разрыва контура мала, в интеграле для вектор-потенциала контурC`можно дополнить да замкнутого контураС

расписывая интеграл для градиента фазы по разрывному контуру получаем:

или

Запишем выражение для полного тока:

Полученное выражение можно переписать в виде аналогичном формуле для стационарного эффекта Джозефсона в одиночном туннельном контакте:

Таким образом мы получили, что максимальное значение сквозного тока через СКВИД существенно зависит от величины магнитного потока через площадь, охватываемую сверхпроводящей петлей. При максимальный ток равен нулю, сверхпроводящее состояние неустойчиво и СКВИД переходит в состояние с конечной проводимостью. Величина потока зависит от площади кольца, что, в силу малости кванта потока позволяет регистрировать очень маленькие магнитные поля. На практике обычно регистрируют изменения магнитного поля, при этом чувствительность СКВИДов достигает величины _{(напомним, что напряженность магнитного поля Земли}

Влияние магнитного поля на Джозефсоновский переход

Для возникновения эффекта Джозефсона необходимо наличие слабой связи двух сверхпроводников. Интересен вопрос, как на такую слабую связь влияет магнитное поле. Рассмотрим джозефсоновский контакт, плоскость с туннельной прослойкой толщиной t и ширинойL. Пусть магнитное поле направлено вдоль осиz, а контакт находится в плоскостиxz. Будем действовать стандартным образом: проведем разрывный контурC` в плоскостиxy, на котором ток равен нулю (для этого контур выбираем на расстоянии λ от берегов разреза), и проинтегрируем выражение для тока. Тем самым мы установим связь скачков фазы на берегах контура с потоком через контур (в интеграле для вектор-потенциала разрывный контур можно безболезненно дополнить до непрерывного). Особенностью вывода служит то, что точки разрыва контура мы выбираем в точкахxиx+Δx, расположенных на малом расстоянии друг от друга.

здесь

Переходя от разности к дифференциалу, находим соотношение, связывающее градиент фазы вдоль контакта и градиент потока

учитывая, что поток через контур равен

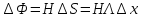
где , получим соотношение, выражающее связь производной фазы и значение магнитного поля в данной точке:

Подставив данное выражение для магнитного поля выражение для тока, описывающее эффект Джозефсона, в уравнение Максвелла получим следующее нелинейное дифференциальное уравнение для фазы

здесь мы ввели новый параметр размерности длины - джозефсоновскую длину. При.

Данное уравнение хорошо известно в математике и физике и называется уравнением «синус-Гордон» (sine-Gorgon). Уравнение «синус-Гордон» относится к числу точно интегрируемых методом обратной задачи рассеяния нелинейных уравнений, и у него существуют солитонные и многосолитонные решения (солитон – уединенная волна). В нашем случае солитонное решение описывает джозефсоновский вихрь.

Рассмотрим частные решения уравнения для фазы.

а) Слабое внешнее поле

для фазы и поля получаем затухающие на масштабе λ_J решения.

б) Солитонное решение.

Перейдем к безразмерной координате и запишем

откуда

с учетом граничного условия

находим

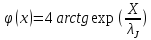
Это и есть солитон уравнения синус-Гордона.

Получили область локализации магнитного поля с циркулирующим вокруг бездиссипативным сверхпроводящим током, представляющую из себя джозефсоновский вихрь. Как и абрикосовский вихрь, джозефсоновский вихрь образован незатухающим циркулирующим током. Однако в отличие от абрикосовского вихря джозефсоновский вихрь не имеет нормальной середины – диэлектрическая туннельная прослойка, в которой расположен центр вихря, вся находится в несверхпроводящем состоянии.

Можно показать, что проникновение дожозефсоновских вихрей в туннельный контакт начинается при магнитном поле, большем критического:

в) Сильное магнитное поле.

При таком поле концентрация вихрей велика, расстояние между ними много меньше джозефсоновской длины, на масштабе которой существенные изменения фазы и магнитного поля в плоскости контакта и, следовательно, магнитное поле можно считать постоянным.

г) Узкий контакт

При влиянием поля джозефсоновских токов можно пренебречь и считать магнитное поле в контакте постоянным и равным внешнему магнитному полю:

Интегрируя уравнение для фазы,

получим выражение для джозефсоновского тока:

Найдем полный ток

где полный поток

и критический ток джозефсоновского котнакта:

В результате мы получили, что максимальное значение тока через котакт определяется выражением

Таким образом, аналогично СКВИДу, зависимость максимального значения бездиссипативного тока от магнитного потока имеет (квази)периодический характер. Отличие от СКВИДа связано с тем, что для одиночного перехода поток определяется площадью перехода, а для СКВИДа – площадью петли.

ВАХ Джозефсоновского перехода.

Рассмотрим простейшую эквивалентную схему джозефсоновского перехода в виде идеального контакта, ток через который определяется уравнением Джозефсона, и параллельного омического сопротивления, которое необходимо для описания ситуации с током через переход боьшим критического.

При

а при

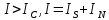
Подставив в выражение для полного тока значения джозефсоновского и омического токов, получим

откуда

Данное уравнение интегрируется тригонометрической подстановкой:

В результате находим выражение для напряжения на переходе, периодически меняющееся во времени:

где частота колебаний напряжения

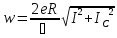
Для среднего значения напряжения на переходе можно получить знакомое выражение

При больших напряжениях и токах вольт-амперная характеристика принимает обычный омический вид

Энергия джозефсоновского контакта.

Запишем выражение для электрической энергии, которая запасается в Джозефсоновском переходе при изменении тока от 0 до .

,

где мы ввели обозначение:

.

При этом затрачивается энергия источника напряжения:

Таким образом для полной энергии имеем:

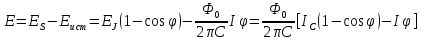
Зависимость энергии от фазы имеет характерный вид («стиральной доски»):

В механике возможны два типа поведения частицы, находящейся в потенциале с таким профилем. Во-первых, частица может находиться в локальном минимуме. Для джозефсоновского перехода этот режим отвечает нулевому напряжению на переходе и протеканию через переход только бездиссипативного джозефсоновского тока. Во-вторых, частица может скатываться вниз с немонотонной зависимостью скорости от времени, преодолевая локальные максимумы потенциала за счет инерции. Для джозефсоновского перехода этот режим отвечает наличию как джозефсоновского бездиссипативного, так и омического диссипативного токов и описывается полученным выше выражением для колебаний напряжения. Конкретный тип движения частицы зависит от начальных условий и массы частицы. При увеличении тока выше критического локальные максимумы и минимумы на зависимости E(φ)исчезают, и остается возможность существования только диссипативного режима. Из условия экстремума

получаем

Что возможно только при . Для описания «инерционных» свойств перехода необходимо усложнить его эквивалентную схему.

Механическая аналогия.

Рассмотрим эквивалентную схему джозефсоновского перехода с учетом его емкости C. В последующих выкладках будем считать скорость светас=1.

В уравнение для тока следует добавить связанный с емкостью ток смещения:

В результате уравнение для фазы принимает фид

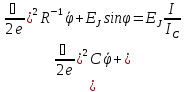
В таком виде уравнение для фазы полностью аналогично уравнению механического массивного маятника:

При этом имеет место следующее соответствие электрических и механических характеристик:

Момент силы тяжести

Если _{(приложенный вращательный момент больше момента силы тяжести), единственный возможнй тип движения – поступательное вращение маятника. При уменьшении параметра I до значения меньше Ic поступательное вращения маятника может сохраниться в силу инерции. Для джозефсоновского перехода такая ситуация отвечает наличию гистерезиса на ВАХ, когда при токе, меньшем критического, на переходе имеется отличное от нуля напряжение и через него течет диссипативный ток.}

Диссипативный ток при гистерезисе сохраняется вплоть до самых малых напряжений. Значение тока на обратной ветке ВАХ при нулевом напряжении называется током возврата. Глубину гистерезиса и величину тока возврата принято характеризовать с помощью так называемого параметра МакКамбера:

где:

Зависимость тока возврата от параметра МакКамбера имеет следующий вид:

Величины этого параметра определяет форму кривых гистерезиса ВАХ:

Макроскопические квантовые эффекты в Джозефсоновских переходах.

Динамика Джозефсоновского перехода описывается уравнением математически идентичным уравнению движения физического маятника в классической механике. При этом джозефсоновская фаза (разность фаза параметров порядка на берегах джозефсоновского перехода, т.е. величина квантовая) играет роль аналогичную углу вращения маятника – сугубо классической переменной. Известно, что переход от классического описания физического маятника к квантово-механическому формально достигается путем применения процедуры квантования. Возникает вопрос: имеют ли физический смысл дискретные уровни энергии и квантованные состояния, возникающие при формальном применении подобной процедуры к джозефсоновскому переходу? Ответ на этот вопрос оказался положительным, и эффекты, связанные с квантованием состояний джозефсоновского перехода экспериментально наблюдались. Поскольку джозефсоновский переход в отличие от элементарных частиц, атомов и молекул, поведение которых подчиняется законам квантовой механики, представляет собой макроскопический объект, такие эффекты получили название макроскопических квантовых эффектов. Их также иногда называют вторичными квантовыми эффектами, поскольку сам по себе эффект Джозефсона представляет собой квантовое явление.

При квантовании физического маятника роль, аналогичную соотношению неопределенности Гейзенберга для координаты и импульса

играет соотношение для фазы и момента вращения M

В состоянии с ограниченным по абсолютной величине моментом вращения фаза точно не определена, что приводит, в частности, к ненулевому значению минимальной энергии квантового маятника (нулевые колебания). Аналогично тому, как для частицы с массой mквантовые свойства усиливаются с уменьшением массы, роль квантовых свойств физического маятника возрастает с уменьшением момента инерцииJ. С учетом установленного выше соответствия между характеристиками джозефсоновского перехода и физического маятника, приходим к выводу, что квантовые свойства джозефсоновского перехода усиливаются с уменьшением его емкостиС.

.

С учетом квантования энергия джозефсоновского перехода уже не представляет собой непрерывную функцию фазы, а квантуется и принимает дискретные значения (см. рис.). Переход между квантованными состояниями, расположенными в различных локальных минимумах потенциальной энергии перехода может происходить как за счет термоактивации, так и за счет туннелирования. При туннелировании вырожденные по энергии уровни перехода должны расщепляться. Такое расщепление наблюдалось

экспериментально, что и послужило доказательством квантовой (вторичной квантовой) природы макроскопических состояний джозефсоновского перехода.

Семинар 10. Микроскопическая теория сверхпроводимости БКШ.Сверхпроводимость как сверхтекучесть электронного газа. Изотопический эффект и электрон-фононное взаимодействие. Задача Купера и природа электрон-электронного притяжения. Модель БКШ и уравнение самосогласования для параметра порядка. Спектр элементарных возбуждений и плотность состояний.

Кратко сформулируем основные положения и идеи микроскопической теории сверхпроводимости Бардина-Купера-Шриффера (БКШ). В основе теории БКШ лежит представление о формировании куперовских пар - связанных состояний двух электронов с противоположными спинами. Куперовские пары образуют сверхпроводящий конденсат, аналогично сверхтекучему конденсату бозонов, и сверхпроводимость можно трактовать как сверхтекучесть заряженных частиц. Природа сверхтекучести тесно связана с явлением бозе-конденсации. Бозе-конденсация возникает при достаточно низких температурах в газе частиц, подчиняющихся статистике Бозе-Эйнштейна, даже в отсутствие взаимодействия между ними. Бозе конденсат становится сверхтекучим при наличии слабого отталкивания между частицами. В сверхпроводнике куперовская пара двух электронов представляет собой бозон, однако этот бозон образован электронами проводимости, делокализованными частицами. Идея описать сверхпроводимость на языке бозонов и бозе-конденсата посещала многих ученых, но последовательная теория была построена только в 1957 г. (БКШ). Неожиданным в их теории оказалось то, что сами по себе куперовские пары образуются одновременно с образованием бозе-конденсата в точке сверхпроводникового перехода.

Для образования куперовской пары два электрона должны

притягиваться друг к другу. Природа межэлектронного притяжения связана с электрон-фононным взаимодействием (испускание и поглощение электронами фононов – обмен фононами). Физически это можно представить себе следующим образом: отрицательно заряженный электрон на пути своего движения притягивает положительно заряженные ионы и вызывает их смещение из положения равновесия. Поскольку масса электрона много меньше массы иона (m<<M) , электрон движется гораздо быстрее иона, и смещение иона сохраняется в течение некоторого времени после того, как электрон покидает окрестность иона. В результате вдоль траектории движения электрона образуется область положительного потенциала (потенциальная яма). Другой электрон, попадая в эту потенциальную яму, понижает свою энергию, что можно трактовать, как опосредованное через колебания решетки (фононы) эффективное межэлектронное притяжение. Поскольку потенциальная яма сохраняется некоторое время в отсутствие создавшего ее (первого) электрона, прямое кулоновское отталкивание электронов при таком процессе несущественно. Из сказанного ясно, что максимальный выигрыш в потенциальной энергии второго электрона будет иметь место, если его траектория повторяет траекторию первого электрона в противоположном направлении, т.е., импульсы двух электронов противоположны.

В приведенной выше картине речь, фактически, идет о связанных колебаниях электронной и ионной плотностей. Оценим более конкретно характерный масштаб энергии электронов, при котором возможно эффективное взаимодействие их с ионами. Волновую функцию пары электронов можно записать в следующем виде:

Откуда для электронной плотности получаем

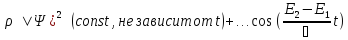
Таким образом для характерной частоты колебаний электронной плотности имеем . Обозначим черезXсмещение ионов из положения равновесия. Уравнение движения дляXимеет вид:

,

где - собственная частота колебаний ионов (порядка дебаевской частоты), параметрf в правой части описывает силу кулоновского взаимодействия электронов и ионов. В результате для амплитуды смещений ионов находим:

,

откуда следует, что при электронные и ионный плотности колеблются синфазно, а при- в противофазе. Взаимодействие двух электронов через обмен фононами, по сути, представляет собой процесс рассеяния. В силу принципа Паули в процессах рассеяния могут участвовать только электроны вблизи поверхности Ферми. Характерная частота колебаний электронной плотности при этом имеет порядок энергии электронных возбуждений вблизи поверхности Ферми. Таким образом синфазные колебания ионной и электронной плотностей возможны, если характерная энергия электронных возбуждений не превышает дебаевской энергии. Такие состояния располагаются в узком пояске вблизи поверхности Ферми шириной

Без учета взаимодействия полная энергия электронного газа равна его кинетической энергии. Основное состояние электронного газа при этом представляет собой сферу Ферми с резкой границей при энергии равной при энергии Ферми.

Заполненная сфера Ферми с резкой границей

Рассмотрим роль взаимодействия и покажем, что с учетом взаимодействия резкая граница заполненных и незаполненных состояний уже не отвечает основному состоянию системы. Запишем волновую функцию системы в виде разложения по базису одночастичных состояний:

– волновая функция одного электрона. Рассмотрим гамильтониан системы в виде суммы оператора кинетической энергии и члена, описывающего взаимодействие:

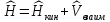
Соответственно, средняя энергия представляет собой сумму кинетической энергии и энергии взаимодействия

Если энергия взаимодействия отрицательна (), т.е. отвечает притяжению частиц, то энергия с учетом взаимодействияможетоказаться ниже, чем в отсутствие взаимодействия. Член с взаимодействием связывает различные квантовые состояния, т.е. описывает процесс рассеяния:

.

Для того, чтобы электроны имели возможность рассеиваться, часть состояний над поверхностью Ферми должна быть заполнена, а часть под поверхностью Ферми – пустыми. тем больше, чем больше количество возможных каналов рассеяния, т.е. чем больше объем той части фазового пространства, которая может участвовать в процессах рассеяния.

Обозначим через импульсы электронов до рассеяния. В результате рассеяния они приобретают импульсы:: :

Для сферической поверхности Ферми максимальный объем фазового пространства достигается при

Таким образом, действительно, в соответствие с нашими качественными рассуждениями энергетически наиболее выгодно парное взаимодействие электронов с равными по величине и противоположно направленными импульсами.

Задача Купера. Куперовские пары.

Покажем, что парное взаимодействие электронов, которое имеет характер притяжения, приводит к образованию их связанного состояния. Это не так очевидно, поскольку речь идет о трехмерной системе. Как известно из квантовой механики, связанное состояние частицы на притягивательном потенциале имеет место при любом, даже сколь угодно слабом потенциале, только в одномерных и двумерных системах. В трехмерной ситуации связанное состояние образуется только в случае достаточно сильного потенциала.

Рассмотрим уравнение Шредингера для двух взаимодействующих электронов, находящихся надповерхностью Ферми:

здесь в операторе ε_Fкинетической энергии мы отсчитываем энергию от уровня Ферми:

,

,

Волновая функция пары невзаимодействующих электронов с противоположными импульсами имеет вид произведения двух плоских волн:

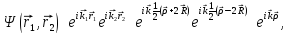
где

Электронам, находящимся в возбужденном состоянии над поверхностью Ферми, соответствует условие 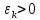. Ищем решение для волновой функции взаимодействующих электронов в виде произвольной суперпозиции таких состояний:

Перегруппируем члены в уравнении Шредингера

Найдем среднее значение энергии:

.

Подставив в это соотношение выражение для волновой функции в виде суперпозиции по состояниям плоских волн, получим:

,

где матричный элемент энергии взаимодействия описывает рассеяние из состояния в состояние :

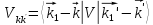
Полученное интегральное уравнение в общем случае требует численного решения. Однако, если сделать некоторые допущения о виде ядра (матричного элемента взаимодействия), то можно получить аналитическое решение. Рассмотрим сепарабельное взаимодействие (допускающее разделение на множители) вида

,

.

Умножим обе части на и просуммируем поk. Сокращая обе части на(при условии), получим следующее уравнение для определения разрешенных значений энергии:

.

Здесь дискретная сумма kпо выполняется по дискретным значениям квазиимпульса, определяемым граничными условиями Борна-Кармана (m_1,2,3–целые):

.

Соответственно, ε_k также принимает дискретный ряд значений. Решение этого уравнения удобно проанализировать графически. График правой части имеет вид, представленный на рисунке. Особенности графика соответствуют нулям знаменателя. Как следует из графика приλ>0все решения расположены в областиE>0и описывают незначительный сдвиг уровней энергии из-за рассеяния. Вместе с тем приλ<0, т.е. при наличии межэлектронного притяжения, появляется дополнительное решениеприE<0,

отвечающее связанному состоянию двух электронов. Это решение существует при любом сколь угодно слабом межэлектронном притяжении. Два электрона в связанном состоянии образуют куперовскую пару.

Более точно определить энергию связанного состояния можно, решив уравнение на собственные значения. Выше мы установили, что межэлектронное притяжение действует в узком энергетическом слое вблизи поверхности Ферми. Пренебрегая угловой зависимостью матричного элемента взаимодействия, выберем определяющие его сомножители в следующем виде:

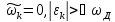
Перейдем в уравнении на собственные значения стандартным образом от суммирования к интегрированию в пределе бесконечного объема системы

где мы учли, что вблизи поверхности Ферми

и . Пусть межэлектронное взаимодействие отвечает притяжению:

.

Введем эффективную константу взаимодействия

где - эффективная плотность состояний на поверхности Ферми. Выполнив интегрирование, получим:

,

В результате находим для энергии связанного состояния

При стремлении эффективной константы взаимодействия к нулю энергия связанного состоянии экспоненциально по обратному параметру взаимодействия стремится к нулю. Именно таким поведением характеризуется энергия связанного состояния от глубины потенциальной ямы в двумерной системе. Данная аналогия имеет глубокий физический смысл и объясняет природу связанного состояния электронов. Электроны, движущиеся в узком слое вблизи поверхности Ферми можно считать эффективно двумерными. Поэтому в соответствии с общим результатом квантовой механики пара таких электронов образует связанное состояние при сколь угодно слабом взаимодействии.

Модель БКШ.

Суммарный спин куперовской пары равен нулю. Однако куперовскую пару нельзя считать обыкновенной бозе-частицой, поскольку радиус связанного состояния двух электрон в пределе слабого взаимодействия существенно больше среднего расстояния между электронами в металле, т. е. куперовские пары сильно перекрываются друг с другом и влияют друг на друга. Поэтому более точно говорить о парных корреляциях в вырожденном Ферми-газе. При этом спаривание происходит не в обычном координатном пространстве, а в импульсном k-пространстве. Теория БКШ описывает сверхпроводящее состояние вырожденного Ферми-газа, обусловленное такими парными корреляциями.

Выше мы установили, что электроны в состояниях могут образовывать связанные состояния. Обозначим черезвероятность того, что пара состоянийзанята. Соответственно через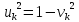- вероятность того, что парапуста. Рассмотрим рассеяние:

.

Обозначим через амплитуду вероятности того, что состояниязаняты, а состояния (– пусты:

.

Аналогичную вероятность при рассеянии

Обозначим через

.

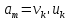Запишем выражение для средней энергии сверхпроводящего состояния с учетом рассеяния

Будем считать, что матричный элемент взаимодействия электронов отличен от нуля только в узком слое толщиной вблизи поверхности Ферми, и заменим его в этой области константой:

Для средней энергии имеем:

.

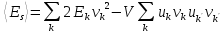С учетом тождества

получим следующее уравнение

.

Введем параметр, который далее будем называть параметром порядка:

.

В результате полученное уравнение принимает вид:

.

С помощью преобразований:

,

приведем его к виду:

,

где мы ввели еще один важный параметр

.

Выбирая физически содержательный () корень уравнения получим решение:

.

При этом если 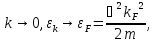то в силу.

График зависимости функции заполнения частиц от квазиимпульса приведен на рисунке:

Исходное уравнение определяет параметр порядка черези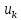, которые, в свою очередь, зависят от. Такое уравнение называется уравнением самосогласования для параметра порядка, или просто уравнением самосогласования.

Рассмотрим решение уравнения самосогласования для параметра порядка:

Введем эффективную константу взаимодействия:

и проинтегрируем уравнение самосогласования

В результате для параметра порядка находим:

Полученное выражение напоминает выражение для энергии связи куперовской пары, но отличается отсутствием двойки в показателе экспоненты. Таким образом параметр порядка существенно превышает по величине энергию связи одиночной куперовской пары, что обусловлено коллективной природой куперовского спаривания в вырожденном Ферми-газе.

Спектр элементарных возбуждений

Определим энергию, необходимую для создания элементарного возбуждения в сверхпроводящем состоянии. Рассмотрим пару электронов в состоянии (). Обозначим черезэнергию пары.

Для w_q можно записать

,

Где фигурирует введенный выше параметр E_q . Рассмотрим ситуацию, когда в сверхпроводник добавлен 1 неспаренный электрон в состоянииq. Энергия неспаренного электрона и есть энергия элементарного возбуждения:

Таким образом мы получили, что введенный выше параметр E_qесть ничто иное, как энергия элементарных возбуждений в сверхпроводнике. При этом минимальная энергия возбуждений соответствует минимальному значению. ДляE_q вблизи уровня Ферми электронов (которые уже не есть элементарные возбуждения) имеем следующий график

:

Здесь линейная функция отвечает линеаризованному закону дисперсии электронов (без учета взаимодействия)

Если неспаренная частица не привносится в сверхпроводник извне, то для создания элементарных возбуждений необходимо разорвать куперовскую пару. Минимальная энергия, необходимая для разрыва куперовской пары равна 2. Процессу создания элементарных возбуждений можно сопоставить следующую энергетическую диаграмму, которая формально подобна закону дисперсии полупроводника:

В отличие от полупроводника, где энергетическая щель, как правило, отвечает дискретному набору точек (или одной точке) в зоне Бриллюэна, в сверхпроводнике энергетическая щель возникает на всей поверхности Ферми. В полупроводнике плотность состояний на краю разрешенной зоны (или, что то же самое, на краю щели) обращается в нуль. В сверхпроводнике из-за того, что краю щели отвечает целая поверхность, плотность состояний g(E)имеет особенность (при ):

.

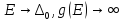Здесь мы учли соотношение:

График зависимости плотности состояний от энергии элементарных возбуждений приведен на рисунке вместе с графиком зависимости энергии элементарных возбуждений от волнового вектора.

Наличие особенности плотности состояний на краю щели послужило ключом к объяснению многих необычных физических свойств сверхпроводников.

Для энергии основного состояния сверхпроводника W₀ можно получить следующее выражение:

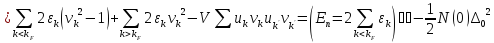
Конечные температуры

Температура перехода в сверхпроводящее состояние служит основной характеристикой сверхпроводника. Еще до создания теории БКШ было замечено, что отношение энергетической щели в сверхпроводящем состоянии вблизи нулевой температуры к температуре сверхпроводящего перехода есть величина, принимающая одно и то же значение для разных сверхпроводников, т.е. независящая от параметров материала.

Рассмотрим сверхпроводник при конечных температурах. Особенностью ситуации при конечных температурах служит то, что над энергетической щелью появляются термически возбужденные неспаренные электроны. С учетом данного обстоятельства для энергии сверхпроводника можем записать

.

Здесь f_k – функция распределения элементарных возбуждений (неспаренных электронов)

Исходя, как и выше, в случае нулевой температуры, из условия минимума энергии

,

получим следующее уравнение самосогласования:

Выражение для энергии элементарных возбуждений через параметр порядка остается таким же, как и при T=0. Переходя от суммирования по квазиимпульсу к интегрированию по энергии, уравнение самосогласования можно привести к виду:

.

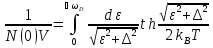Данное уравнение определяет зависимость параметра от температуры , и в общем случае требует численного решения. В пределепараметр порядка также стремится к нулюи из уравнения самосогласования мы получаем уравнение для температуры сверхпроводящего перехода.

Решение данного уравнения дает следующее значение температуры перехода:

Из сравнения выражений для параметра порядка при нулевой температуре и для температуры перехода, приходим к замечательному результату, что их отношение не зависит от параметров материала:

Множитель «двойку» в числителе удобно использовать в связи с тем, что на эксперименте (например, по поглощению инфракрасного излучения) определяется именно величина энергетической щели 2Δ. Данный результат находится в полном соответствии с экспериментом для низкотемпературных сверхпроводников, и он послужил одним из решающих аргументов в пользу справедливости теории БКШ.

Семинар 11. Приборы и элементы интегральных схем на основе джозефсоновских переходов. Стандарт напряжения. Запоминающий элемент с неразрушающим считыванием. Логический элемент на джозефсоновских переходах. Гистерезис ВАХ и проблема «защелки». Использование квантов потока для хранения и обработки информации и быстрая одноквантовая логика.

Явление сверхпроводимости используется в разнообразных аналоговых и цифровых приборах. Некоторые из них, например, криотрон и сквид, мы уже рассмотрели. Продолжим знакомство со сверхпроводящими приборами и устройствами.

Стандарт напряжения.

Одно из наиболее важных, наряду со сквидами, приложений сверхпроводников в аналоговой электронике представляют собой стандарты напряжения. Из выражения для тока в нестационарном эффекте Джозефсона при постоянном напряжении на переходе следует, что среднее значение тока по времени равно нулю. Рассмотрим ситуацию, когда на джозфсоновском переходе присутствует как постоянное напряжение V₀, так и переменное напряжениеV₁(t)=-V₁cos(ωt). Решив уравнение для фазы, получим выражение для джозефсоновского тока:

Можно показать, что среднее значение этого тока по времени уже не равно нулю. Выполним разложение функции «синус от синуса» в ряд по функциям Бесселя целого порядка J_n:

.

Как нетрудно видеть при

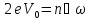
среднее значение тока отлично от нуля и равно

.

В эксперименте измеряется именно среднее значение тока. Поэтому при наличии на джозефсоновском переходе одновременно постоянного V₀и переменного смещенияV₁(t) данный эффект будет проявлять себя в возникновении на вольт-амперной характеристике перехода ступенек тока на фоне зависимости:

Такие ступеньки называют ступеньками Шапиро. Величина скачка тока зависит от амплитуды переменного напряжения и других параметров, но само положение скачка на оси V₀определяется только частотой и мировыми постоянными. Поскольку для определения частоты имеются высокоточные стандарты, данный эффект можно использовать для определения напряжения с высокой точностью и создания стандарта напряжения.

Ячейка памяти на основе криотрона.

Криотрон (описанный выше в разделе 5) представляет собой сверхпроводниковый элемент (джозефсоновский переход или просто тонкая проволочка), который под действием магнитного поля скачком переходит в резистивное состояние, что сопровождается скачкообразным изменением приложенного напряжения. На базе такого элемента могут быть построены различные логические устройства и ячейки памяти. Простейший вариант ячейки памяти представлен на рисунке и состоит из сверхпровдящего контура с криотроном на базе джозефсоновского перехода и управляющим проводником, через который пропускают управляющий ток I_c. Через контур пропускается вентильный токI_g. Двоичная информация хранится в виде незатухающего тока, циркулирующего в сверхпроводящем контуре «по» или «против» часовой стрелки. Запись информации осуществляется подачей импульсов тока управляющего и вентильного токов.

L₂<L₁

Временная диаграмма работы устройства приведена на рисунке. Импульс управляющего тока I_c длительностьюt_imсоздает магнитное поле, которое переводит джозефсоновский переход в резистивное состояние. После прекращения действия управляющего тока джозефсоновский переход возвращается в сверхпроводящее состояние с нулевым сопротивлением за времяt₀. Состояние замкнутого сверхпроводящего контура при этом зависит от длительности импульса вентильного тока. Запись информации возможна только, если длительности импульса вентильного тока превышает длительность импульса управляющего токаt_im на величину, превышающуюt₀. В противном случае, как следует из диаграммы, информация стирается и ток в контуре после восстановления сверхпроводящего состояния отсутствует.

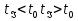
После перехода джозефсоновского перехода в резистивное состояние вентильный ток протекает в левом плече контура. При этом он создает магнитный поток через замкнутый, но в течение времени t₀не сверпроводящий контур. Если длительность импульса вентильного тока превышает время восстановления сверхпроводимостиt₀, то спустя времяt₀ мы имеем ситуацию с магнитным потоком, пронизывающим уже сверхпроводящий контур. После выключения вентильного тока этот поток сохранится за счет возбуждения в контуре незатухающего сверхпроводящего тока. Таким образом, если в исходном состоянии ток обращался по часовой стрелке (логическая «1»), то при подаче импульса вентильного тока, текущего сверху вниз, после его выключения в контуре возникнет замкнутый ток, текущий против часовой стрелки (логический «0»). При подаче следующего импульса вентильного тока аналогичной полярности состояние логического «0» не изменится. Для записи «1» следует подать импульс вентильного тока противоположной полярности (направление тока - снизу вверх).

Запоминающий элемент с неразрушающим считыванием

Информация, как и в предыдущем примере, кодируется незатухающим током, циркулирующим в контуре В₀В₁А₂А₁.Логическому «0» соответствует циркуляция тока против часовой стрелки, логической «1» - по часовой стрелке. Пусть исходное состояние ячейки – «0».

Для записи «1» подаются токи и. При этом через переход А₁течет ток. Токподбирается таким образом, чтобы при параллельном направлении токоввентиль В₀закрылся. В результате токвозрастает до тех пор, покане уменьшается до величины такой, что открывается переход В₀. Теперь ужеи при выключениив контуре возбуждается ток, текущий по часовой стрелке, т.е. происходит запись «1».

Считывание информации без разрушения происходит на переходеS: включаются токиI_wиI_i, если при этом оказывается, что ток через переход А₂равен(ток в контуре циркулирует по часовой стрелке – «1»), то переходSпереключается в резистивное состояние. Если же ток циркулирует против часовой стрелки («0»), тои магнитное поле этого тока недостаточно велико, чтобы произошло переключение переходаS. Для записи «0» следует подать токи изменить направление тока.

Логические элементы на джозефсоновских переходах.

Логический элемент состоит их трех управляющих шин А, В и С и криотрона на джозефсоновском переходе. Магнитные поля параллельных токов складываются, антипараллельных – вычитаются. Помимо магнитного поля управляющего тока на джозефсоновский переход также воздействует поле вентильного тока, протекающего непосредственно через переход.

Из-за того, что управляющий и вентильный токи в рассматриваемом примере также могут протекать параллельно или антипараллельно, график зависимости максимального значения вентильного тока от величины управляющего тока асимметричен относительно изменения направления управляющего тока. Область резистивного состояния на графике расположена сверху колоколообразной кривой. Считаем, что величина тока через управляющий проводник принимает значение либо 0, либо i. В отсутствие управляющего тока система находится в состоянии, характеризуемом точкой а. При параллельной ориентации вентильного и управляющего токов криотрон переходит в резистивное состояние, если ток течет хотя бы по одному управляющему проводнику (точкаb). Такое поведение системы соответствует логической функции «ИЛИ». При антипараллельном направлении управляющего и вентильного токов наличия тока в одном (точка с) или в двух (точкаd) проводниках недостаточно, чтобы перевести криотрон в резистивное состояние. Вентиль срабатывает, только если ток течет по всем трем управляющим проводника (точка е). Такое поведение системы описывается логической функцией «И».

Заметим, что сверхпроводниковым цифровым электронным устройствам, работа которых основана на переключении джозефсоновского перехода в резистивное состояние внутренне присущ серьезный недостаток, связанный с гистерезисным характером вольт-амперной характеристики такого перехода. При возвращении к исходным значениям тока переход остается врезистивном состоянии с ненулевым значением напряжения. Такой эффект называется «защелкой» («latching»). Для устранения «защелки» после завершения операции приходится обнулять все значения токов в системе. Другой способ связан с уменьшением области гистерезиса путем шунтирования перехода малым сопротивлением, что приводит к уменьшению параметра Маккамбера.