Программа – минимум по курсу «Теория вероятностей и математическая статистика»

ЭКТ – 2 (4-й семестр, 2011-2012 учебный год)

Студент должен:

1. Формулировать три основные аксиомы вероятности: неотрицательности, нормированности и -аддитивности.

2. Знать классическое определение вероятности.

3. Владеть понятием геометрической вероятности.

4. Знать определения условной вероятности, несовместности и независимости событий.

5. Формулировать теоремы сложения и умножения.

6. Знать формулу полной вероятности.

7. Знать формулы Байеса.

8. Владеть понятием случайной величины (СВ), объяснять, что такое множество возможных значений и ряд распределения СВ.

9. Знать определение и основные свойства одномерной функции распределения.

10. Знать определение и основные свойства одномерной плотности распределения.

11. Знать определения математического ожидания, дисперсии, среднего квадратического отклонения, моментов (начальных и центральных), моды для случая конечного вероятностного пространства. Уметь их вычислять.

12. Для СВ, имеющих плотность распределения, знать формулы для вычисления математического ожидания, дисперсии, моментов (начальных и центральных). Уметь их вычислять.

13. Для СВ, имеющих плотность распределения, уметь находить моду, медиану.

14. Знать следующие виды распределений СВДТ: биномиальное и пуассоновское.

15. Знать формулы для вычисления математического ожидания и дисперсии СВ, имеющих биномиальное и пуассоновское распределения.

16. Знать следующие виды распределений СВНТ: равномерное и нормальное.

17. Знать определение совместной функции распределения, её основные свойства.

18. Знать определение закона совместного распределения системы двух дискретных СВ.

19. Уметь получать законы распределения отдельных компонент по таблице распределения двумерной дискретной СВ.

20. Знать определение двумерной плотности распределения, её основные свойства.

21. Владеть понятием независимости СВ, знать необходимые и достаточные условия независимости СВ.

22. Уметь вычислять основные числовые характеристики двумерных дискретных СВ: математические ожидания и дисперсии компонент, ковариацию и коэффициент корреляции.

23. Знать определения: выборки, вариационного ряда, полигона, гистограммы, эмпирической функции распределения.

24. Знать определения основных числовых характеристик выборки и формулы для их вычисления (для негруппированных данных): выборочных среднего и дисперсии; моды и медианы.

25. Знать основные требования, предъявляемые к точечным оценкам параметров генеральной совокупности, а также формулу для несмещённой оценки дисперсии (для негруппированных данных).

26. Знать определения доверительного интервала и доверительной вероятности.

1. Три основные аксиомы вероятности.

Тройка (, A, P), где

 – это пространство элементарных событий(достоверное событие);

A – -алгебра подмножеств  , называемых событиями;

P – числовая функция, определенная на событиях и называемая вероятностью.

P называется вероятностным пространством, если выполнены следующие аксиомы:

A1. P(A)  0, A  A. (неотрицательнность).

A2. P() = 1 (нормированность P).

A3. (-аддитивность)

2. Классическое определение вероятности.

Пусть заданы неотрицательные числа , которые удовлетворяют следующему требованию , тогда вероятность события (*) (способ введения вероятности на конечном вероятностном пространстве).

Очевидно, что так определенная вероятность вместе будет удовлетворять всем аксиомам.

Обозначим через – количество элементов в множестве .

Частным случаем определения вероятности по формуле (*) будет так называемое классическое определение вероятностей, когда все будут равны друг другу, так как

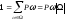
; – формула классической вероятности (**)

3. Геометрическая вероятность.

Геометрические вероятности – класс моделей вероятностных пространств, дающий геометрические вероятности.

Пусть Ω={ω} – ограниченное множество n-мерного евклидова пространства с конечным n-мерным объёмом.

Событиями назовём подмножества Ω, для которых можно определить n-мерный объём.

Для любого A  A положим

, где |V|-n-мерный объем множества V  A.

4. Условная вероятность, несовместность и независимость событий.

Пусть P(B)>0.

Условной вероятностью P(A|B) события A при условии, что событие B произошло, называется отношение .

События A и B называют несовместными, если событие A×B не может

произойти. (PABPAPBPAB

События A и B называют независимыми, если

P(A×B) = P(A)× P(B) .

5. Теоремы сложения и умножения.

Теорема о вероятности суммы двух событий:

P(A+ B) = P(A)+ P(B)- P(A×B), для любого A,B  A

Следствие 1. Для несовместных событий A и B выполнено соотношение

P(A+ B) = P(A)+ P(B)

Следствие 2. Для противоположного события A выполнено соотношение

P(A) =1- P(A)

Теорема о вероятности произведения двух событий:

P(A×B) = P(A)×P(B|A)

6.Формула полной вероятности.

Если – разбиение и все , то для всех событий B . (гипотезы)

7.Формулы Байеса

Теорема. Если – разбиение и все , тогда имеет место следующая формула:

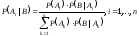
Доказательство:

По теореме умножения:

8. Случайная величина, мн-во возможных значений и ряд распределения СВ.

Пусть (Ω, A, P) – произвольное вероятностное пространство.

Определение. Числовая функция 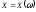от элементарного события называется случайной величиной (СВ), если

 A (*)

Множество возможных значений случайных величин X называется область значений числовой функции . Если это множество является конечным или счетным, то случайная величина называется случайной величиной дискретного типа (СВДТ). Если это множество является несчетным, то случайная величина называется случайной величиной непрерывного типа (СВНТ).

Рядом распределений СВДТ Х называется таблица

X	x1	x2	…	xn	…
P	p1	p2	…	pn	…

9.Определение и основные св-ва одномерной функций распределения.

Функция называется функцией распределения СВ Х .

Функция обладает следующими свойствами:

1. – не убывает;

2. – непрерывна слева;

3. ;

4. .

10.Определение и основные св-ва одномерной плотности распределения.

Функция есть плотность распределения СВ X, если

Свойства

1.

Замечание.

Для СВ X имеющей функции. Плотности из свойства 1 и теоремы из курса математического анализа (о непрерывности интеграла с переменным верхним пределом)  что непрерывна.

2. в точках непрерывности .

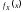3. .

4. , т.к. 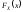неубывающая функция, то .

5. Условия нормировки:.

11. Определения мат. Ожидания, дисперсии, среднего квадратичного отклонения, моментов (начальных и центральных), моды для случая конечного вероятностного пространства. Уметь их вычислять.

Пусть вероятность P на конечном вероятностном пространстве (, A , P) определяется с помощью элементарных вероятностей .

Определение. МО случайной величины называется сумма .

Положим .

Определение. Начальным моментом S-го порядка СВ Х называется .

Обозначим .

Определение. Центральным моментом S-го порядка называется .

Определение. Центральный момент II-го порядка () называется дисперсией СВ Х и обозначается .

Определение. – называется средним квадратическим отклонением СВ Х (стандартным отклонением в литературе).

Определение. Модой СВДТ Х называется такое возможное значение , для которого .

Модой СВНТ Х называется действительное число , являющееся точкой максимума функции плотности вероятностей .

12.Для СВ имеющих плотность распределения, знать формулы для вычисления МО, дисперсии, моментов. Уметь их вычислять

МО.

1. Х – СВДТ.

Если Х принимает счетное множество значений с вероятностями и ряд сходится абсолютно, то .

2. Х – СВНТ.

Если СВ Х имеет плотность и (сходится), то .

Начальный момент.

Для СВДТ:

Для СВНТ: .

Центральный момент.

Для СВДТ:

.

Для СВНТ:

.

Дисперсия.

Для СВДТ:

.

Для СВНТ:

.

13.Для СВ имеющих плотность распределения, уметь находить моду, медиану.

Модой СВДТ Х называется такое возможное значение , для которого .

Модой СВНТ Х называется действительное число , являющееся точкой максимума функции плотности вероятностей .

Медианой СВ Х называется действительное число , удовлетворяющее условию: , то есть это корень уравнения .

Эта характеристика применяется, как правило, только для СВНТ и геометрически медиана, это абсцисса той точки на оси ОХ, для которой площади под графиком лежащие слева и справа от нее одинаковы и равны .

14.Биномиальное и пуассоновское распределение СВДТ.

Определение. СВДТ Х имеет биномиальное распределение, если ее возможные значения 0, 1, 2, …, m, …, n, а соответствующие вероятности

Это распределение зависит от двух параметров: n, p.

Определение. СВДТ Х имеет распределение Пуассона, если ее возможные значения 0, 1, 2, …, m, … (счетное множество значений), а соответствующие вероятности выражаются формулой .

15.Формулы для вычисления МО и дисперсии СВ, биномиального и пуассоновского распределения.

Биномиальное:

Пуассоновское:

16.Равномерное и нормальное распределение СВНТ.

Определение. СВНТ Х называется распределенной равномерно на , если , .

Определение. СВНТ Х называется распределенной по нормальному (Гауссовскому) закону с параметрами , если плотность распределения вероятности имеет вид.

Нормальное распределение задается двумя параметрами m и .

17.Совместная функция распределения и ее основные св-ва.

Рассмотрим в одном и том же вероятностном пространстве (,A,P) набор СВ . Так как множество A, таких пересечения A, поэтому существует вероятность этого события, которая называется многомерной функцией распределения.

.

Свойства.

1. 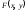по каждому аргументу не убывает и непрерывна слева.

2. .

3. .

4. а) При становится функцией распределения компоненты x.

.

б) При становится функцией распределения компоненты y.

.

18.Закон совместного распределения систем двух дискретных СВ.

Определение. Двумерная СВ (X, Y) называется дискретной, если каждая из СВ и Х и Y является дискретной.

Пусть СВ Х может принимать значения , а СВ Y принимает дискретные значения .

Y X	y1	y2	…	ym	P{X=xi}
x1	P11	P12	…	P1m	P1
x2	P21	P22	…	P2m	P2
…	…	…	…	…	…
xn	Pn1	Pn2	…	Pnm	Pn
P{Y=yj}	P1	P2	…	Pm	

Двумерный случайные вектор может принимать только пары значений

По этой таблице нетрудно определить функцию распределения.

.