
- •Компьютерный практикум 1 Однокритериальный выбор в условиях определенности. Нелинейные задачи
- •Порядок выполнения
- •Краткие теоретические сведения и практические упражнения
- •1. Постановка однокритериальной задачи принятия решений в условиях определенности
- •2. Функция fmincon
- •Список рекомендуемой литературы
2. Функция fmincon
Функция fmincon
вычисляет вектор
![]() ,
который является локальным минимумом
скалярной функции
,
который является локальным минимумом
скалярной функции![]() векторного аргумента
векторного аргумента![]() при следующих ограничениях:
при следующих ограничениях:
1) линейных неравенств
![]() (здесь
(здесь![]() - матрица,
- матрица,![]() - вектор);
- вектор);
2) линейных равенств
![]() (здесь
(здесь![]() - матрица,
- матрица,![]() - вектор);
- вектор);
3) ограничений на
величину вектора
![]() :
:![]() (здесь
(здесь![]() и
и![]() - векторы).
- векторы).
Также дополнительно
могут быть наложены нелинейные условия:
![]() и
и![]() (здесь
(здесь![]() и
и![]() - векторные нелинейные функции), однако
в данной лабораторной работе мы нелинейные
ограничения рассматривать не будем.
- векторные нелинейные функции), однако
в данной лабораторной работе мы нелинейные
ограничения рассматривать не будем.
Условия применения fmincon:
1) Минимизируемая
функция
![]() должна быть непрерывной функцией
аргументов;
должна быть непрерывной функцией
аргументов;
2) Значения функций
![]() должны быть действительными (не
комплексными!) .
должны быть действительными (не
комплексными!) .
Обратите внимание,
что задача, которую решает функция
fmincon
не совпадает со скалярной задачей
минимизации, поскольку в общем случае
функция fmincon
находит локальные
минимумы функции
![]() ,
а скалярная задача оптимизации заключается
в поиске наименьшего значения функции
(т.е.глобального
минимума). Отметим два случая, когда эти
задачи совпадают:
,
а скалярная задача оптимизации заключается
в поиске наименьшего значения функции
(т.е.глобального
минимума). Отметим два случая, когда эти
задачи совпадают:
1. Функция fmincon
ищет глобальный минимум, если единственными
ограничениями являются ограничения на
величину вектора
![]() :
:![]() .
.
2. Функция fmincon
ищет глобальный минимум, если единственными
ограничениями являются линейные
равенства
![]() .
.
Перечисленные случаи не единственные, и ниже мы вернемся к обсуждению этого вопроса.
Заметим, что когда
минимум не находится во внутренних
точках допустимой области, fmincon
минимизирует
![]() в граничных точках области.
в граничных точках области.
Виды функции fmincon:
![]() (здесь
(здесь
![]() - выражение минимизируемой функции в
апострофах, или имя в апострофах М-файла
этой функции, или указатель на функцию,
если она определена в виде М-файла;
- выражение минимизируемой функции в
апострофах, или имя в апострофах М-файла
этой функции, или указатель на функцию,
если она определена в виде М-файла;![]() - вектор, начиная с которого идет поиск
минимума функции
- вектор, начиная с которого идет поиск
минимума функции![]() );
);
![]() ;
;
![]() .
.
Если какой-то из
перечисленных выше входных параметров
не используется, вместо него задается
пустой аргумент ([]). Если отсутствуют
ограничения на отдельные компоненты
![]() сверху или снизу, то соответствующие
компоненты векторов
сверху или снизу, то соответствующие
компоненты векторов![]() и
и![]() задаются как
задаются как![]() (
(![]() )
или
)
или![]() (
(![]() ).
).
Чтобы получить
значение критерия оптимальности
![]() в найденной точке, нужно использовать
более полное обращение к каждому виду
функцииfmincon:
в найденной точке, нужно использовать
более полное обращение к каждому виду
функцииfmincon:
![]() (здесь
(здесь![]() - минимальное значение функции
- минимальное значение функции![]() ).
).
Пример 1.
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Решение. Поскольку
в задаче есть только ограничения на
величину вектора
![]() ,
то с помощью функцииfmincon
можно найти глобальный минимум, т.е.
задачу оптимизации.
,
то с помощью функцииfmincon
можно найти глобальный минимум, т.е.
задачу оптимизации.
>> x0=[1,1,3];
>> lb=[1,0,0];
>> ub=[3,5,Inf];
>> [x,feval]=fmincon('x(1)^2+x(2)^2+x(3)^2-4*x(1)-6*x(2)-8*x(3)',x0,[],[],[],[],lb,ub)
x =
2.0000 3.0000 4.0000
feval =
-29.0000
Выводы: решением
задачи минимизации является точка с
координатами (2,3,4). Наименьшее значение
функции
![]() равно
равно![]() .
.
Пример 2.
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Решение.
Чтобы прояснить ситуацию, построим график минимизируемой функции:
>> [X1,X2]=meshgrid(0:0.05:3,0:0.05:3);
>> f=X1.^2+X2.^2-X1.*X2-X1-X2;
>> surf(X1,X2,f)
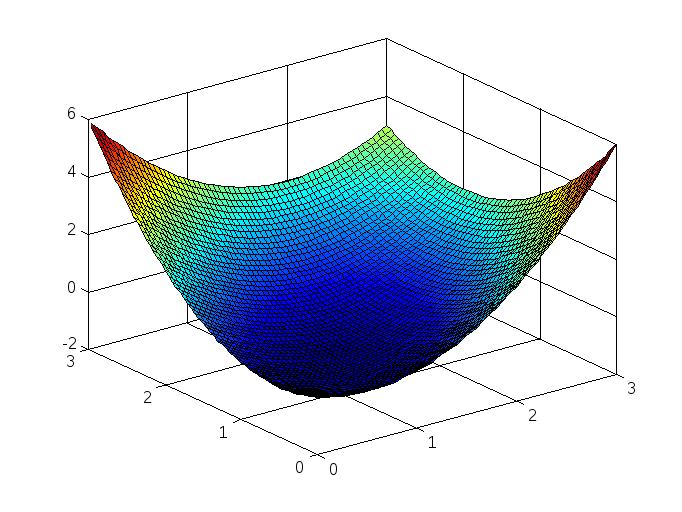
На рисунке видно, что на допустимом множестве есть только один локальный минимум и этот локальный минимум совпадает с наименьшим значением функции на допустимом множестве. Для нахождения минимума (в данном случае как локального, так и клобального) используем функцию fmincon. В качестве начальной точки x0 возьмем точку с координатами (0,5; 0,5) (эта точка удовлетворяет ограничениям) .
>> A=[1 1];
>> B=[3];
>> lb=[0 0];
>> ub=[Inf Inf];
>> x0=[0.5 0.5];
>> [x,feval]=fmincon('x(1)^2+x(2)^2-x(1)*x(2)-x(1)-x(2)',x0,A,B,[],[],lb,ub)
x =
1 1
feval =
-1
Выводы: решением
задачи минимизации является точка с
координатами (1,1). Наименьшее значение
функции
![]() равно
равно![]() .
.
3. Решение задачи потребительского выбора.
Будем считать, что
потребитель располагает доходом
![]() ,
которые он может полностью потратить
на приобретение продуктов. Рассмотрим
потребительские набор из двух продуктов.
Потребительский набор – это вектор
,
которые он может полностью потратить
на приобретение продуктов. Рассмотрим
потребительские набор из двух продуктов.
Потребительский набор – это вектор![]() ,
координата
,
координата![]() которого равна количеству единиц первого
блага, а
которого равна количеству единиц первого
блага, а![]() равна количеству единиц второго блага.
На множестве потребительских наборов
равна количеству единиц второго блага.
На множестве потребительских наборов![]() определена функция
определена функция![]() (называемаяфункцией
полезности потребителя),
значение
(называемаяфункцией
полезности потребителя),
значение
![]() которой на потребительском наборе
которой на потребительском наборе![]() равно потребительской оценке потребителем
этого набора. Каждый потребитель имеет,
вообще говоря, свою функцию полезности
(на тот счет, как именно нужно строить
функию полезности, у экономистов есть
много прледложений).Задача
постребительского выбора
(задача рационального поведения
потребителя на рынке) заключается в
выборе такого потребительского набора
равно потребительской оценке потребителем
этого набора. Каждый потребитель имеет,
вообще говоря, свою функцию полезности
(на тот счет, как именно нужно строить
функию полезности, у экономистов есть
много прледложений).Задача
постребительского выбора
(задача рационального поведения
потребителя на рынке) заключается в
выборе такого потребительского набора
![]() ,
который максимизирует его функцию
полезности при заданном бюджетном
ограничении. Бюджетное ограничение
означает, что денежные расходы на
продукты не могут превышать денежного
дохода, т.е.
,
который максимизирует его функцию
полезности при заданном бюджетном
ограничении. Бюджетное ограничение
означает, что денежные расходы на
продукты не могут превышать денежного
дохода, т.е.![]() , где
, где![]() и
и![]() - рыночные цены одной единицы первого
и второго продуктов соответственно, а
- рыночные цены одной единицы первого
и второго продуктов соответственно, а![]() - доход индивидуума, который он готов
потратить на приобретения первого и
второго продуктов (величины
- доход индивидуума, который он готов
потратить на приобретения первого и
второго продуктов (величины![]() ,
,![]() ,
,![]() -заданы).
-заданы).
Формально задача потребительского выбора в случае двух продуктов имеет вид
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Упражнение 1.
Указание. Выполнение заданий следует начать с геометрической иллюстрации, с тем чтобы получить представление о возможности использования функции fmincon для решения приведенных заданий и правильно интерпретировать полученные результаты.
В1) Решить задачу потребительсткого выбора
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В2) Решить задачу потребительского выбора
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В3) Решить задачу потребительского выбора
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В4) Решить задачу потребительсткого выбора
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4. Решение задач скалярной оптимизации в случае выпуклых функции при линейных ограничениях с помощью функции fmincon.
Множество
![]() называетсявыпуклым,
если вместе с любыми двумя точками
называетсявыпуклым,
если вместе с любыми двумя точками
![]() и
и![]() оно содержит и отрезок, соединяющий эти
точки, т.е.
оно содержит и отрезок, соединяющий эти
точки, т.е.![]() для всех
для всех![]() .
.
Функция
![]() , заданная на выпуклом множестве
, заданная на выпуклом множестве![]() ,
называетсявыпуклой
на этом множестве, если для любых точек
,
называетсявыпуклой
на этом множестве, если для любых точек
![]() и
и![]() и произвольного числа
и произвольного числа![]() справедливо неравенство
справедливо неравенство
![]() .
.
Если при этом
![]() и неравенство строгое, то функция
называетсястрого
выпуклой.
и неравенство строгое, то функция
называетсястрого
выпуклой.
На практике обычно
используют следующий критерий выпуклости
функции: если
![]() дважды дифференцируемая на выпуклом
множестве
дважды дифференцируемая на выпуклом
множестве![]() функция и все угловые миноры матрицы
ее вторых производных
функция и все угловые миноры матрицы
ее вторых производных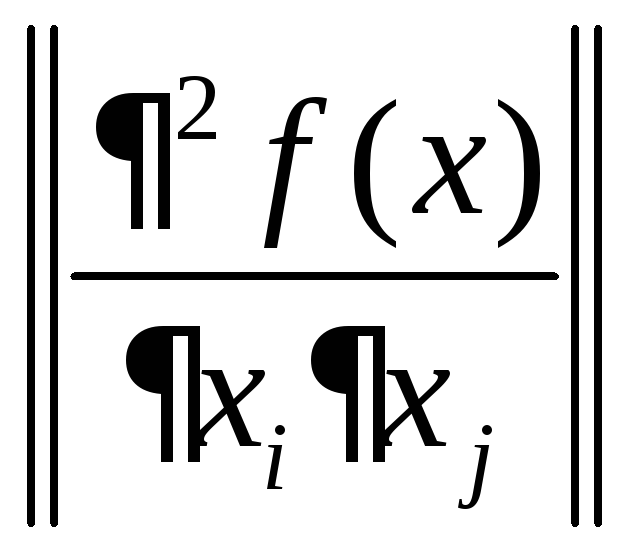 (гессиана) неотрицательны (положительны)
при всех
(гессиана) неотрицательны (положительны)
при всех![]() , то функция
, то функция![]() является выпуклой (строго выпуклой) на
множестве
является выпуклой (строго выпуклой) на
множестве![]() .
.
Задача скалярной оптимизации
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
называется выпуклой,
если
![]() ,
,![]() , …,
, …,![]() выпуклые функции.
выпуклые функции.
Выпуклые задачи имеют следующие свойства:
1) если задача скалярной оптимизации выпукла, то всякий локальный минимум является одновременно и глобальным;
2) если задача
скалярной оптимизации выпукла, имеет
решение и функция
![]() строго выпукла на
строго выпукла на![]() , то решение задачи единственно.
, то решение задачи единственно.
Упражнение 2. Построить математические модели приведенных задач, убедиться в их выпуклости, после чего решить, используя функцию fmincon.
В1) Пусть имеется
предприятие, выпускающее определенный
товар и использующее при этом три вида
ресурсов. Объемы затрачиваемых ресурсов
обозначим через
![]() ,
,![]() ,
,![]() .
Работа предприятия характеризуется
производственной функцией Кобба-Дугласа
.
Работа предприятия характеризуется
производственной функцией Кобба-Дугласа![]() . Пусть цена
. Пусть цена![]() единицы первого ресурса равна 4 евро,
цена
единицы первого ресурса равна 4 евро,
цена![]() единицы второ го ресурса равна 6 евро,
цена
единицы второ го ресурса равна 6 евро,
цена![]() единицы третьего ресурса равна 2 евро.
На следующий месяц предприятие может
затратить на оплату ресурсов не более
48000 евро. Какие ресурсы и в каком количестве
предприятие должно оплатить в следующем
месяце, имея целью максимизацию объема
выпуска товара.
единицы третьего ресурса равна 2 евро.
На следующий месяц предприятие может
затратить на оплату ресурсов не более
48000 евро. Какие ресурсы и в каком количестве
предприятие должно оплатить в следующем
месяце, имея целью максимизацию объема
выпуска товара.
В2) Фирма, производящая продукцию на трех заводах, решила выпускать в месяц не менее 210 единиц продукции при наименьших суммарных. Сколько продукции ежемесячно следует выпускать на каждом заводе, если функции издержек заводов имеют вид:
![]() для первого завода;
для первого завода;
![]() для второго завода;
для второго завода;
![]() для третьего
завода?
для третьего
завода?
