
3.2.1. 3.2.2.
3.2.3.
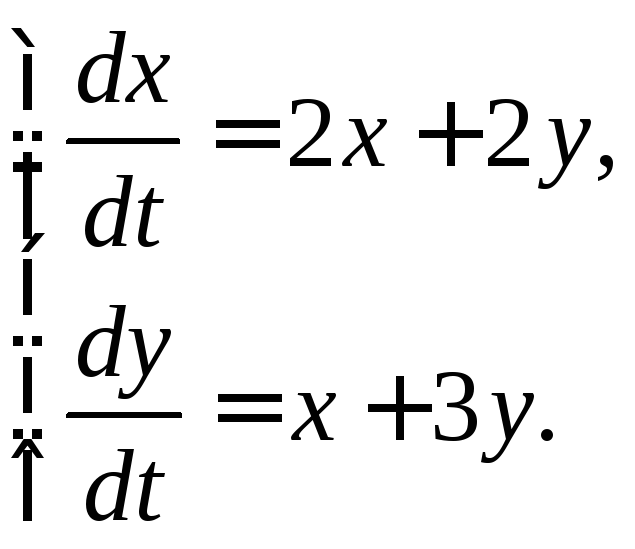 3.2.4.
3.2.4.
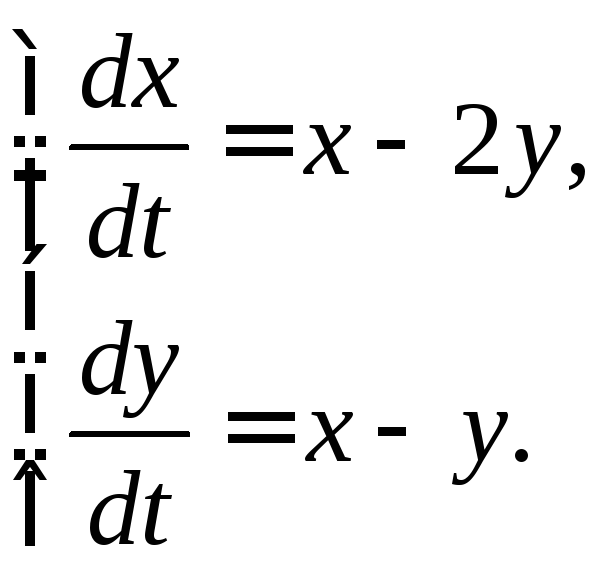
3.2.5.
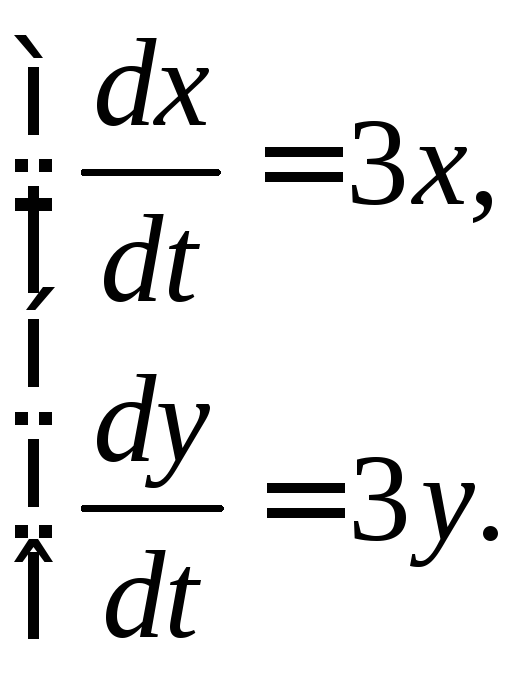 3.2.6.
3.2.6.
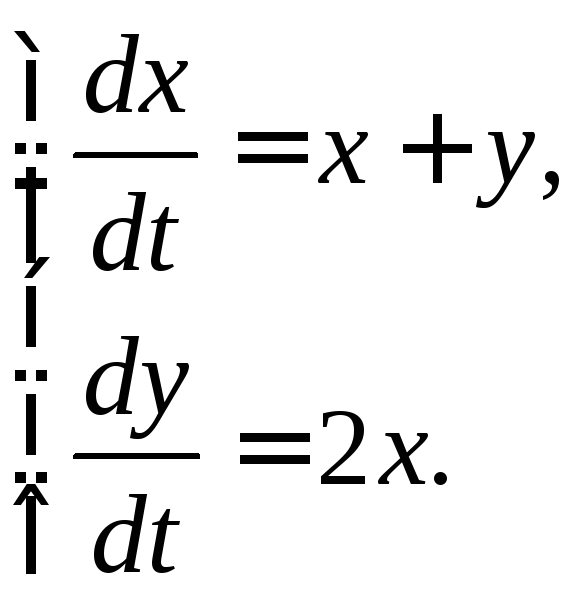
3.2.7.
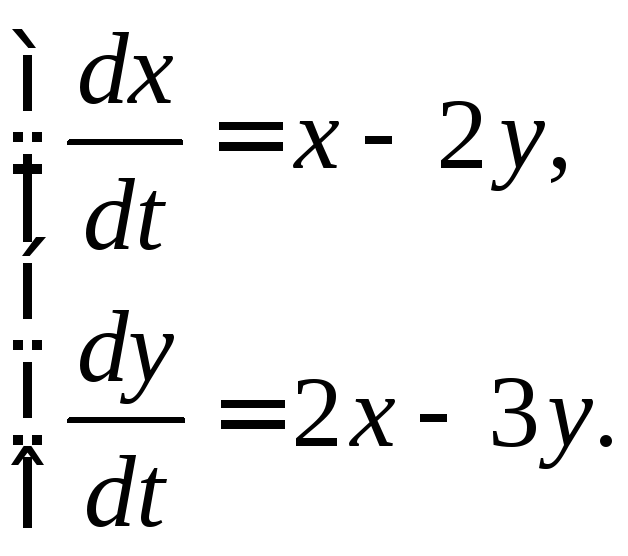 3.2.8.
3.2.8.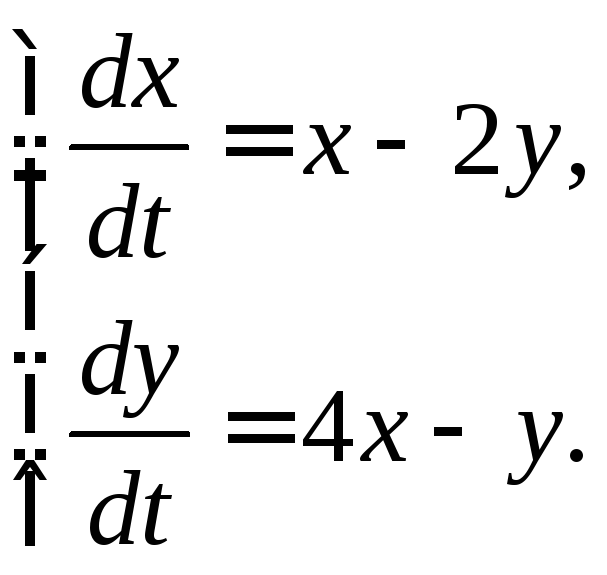
3.2.9.
 3.2.10.
3.2.10.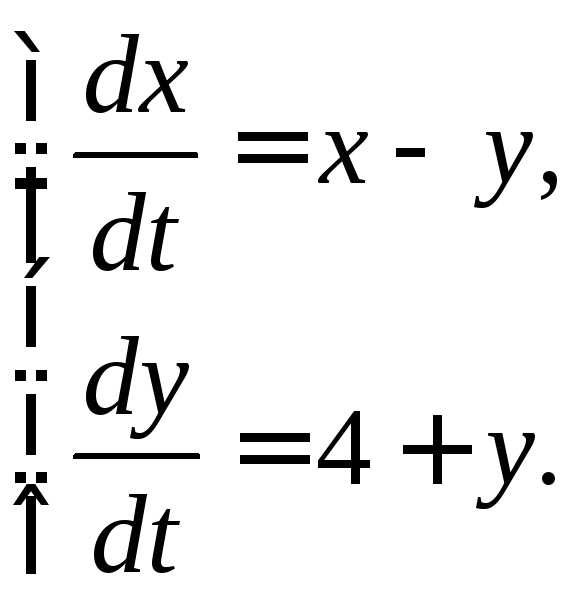
3.2.11.
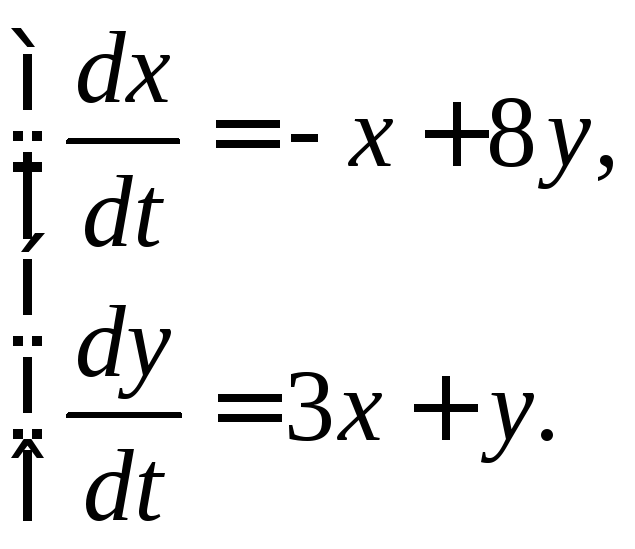 3.2.12.
3.2.12.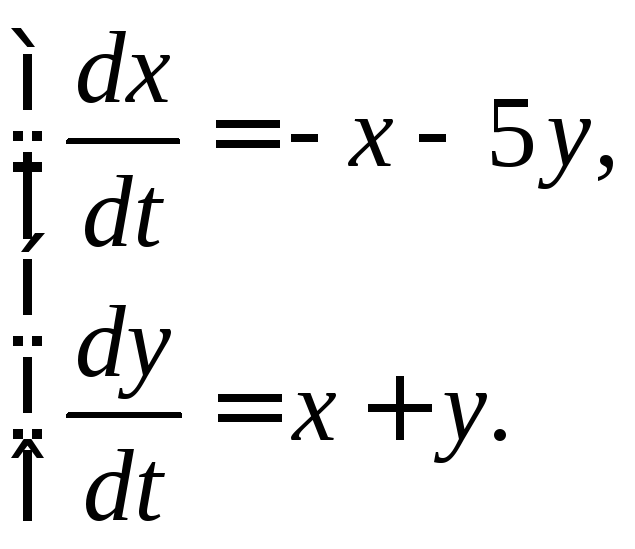
3.2.13.
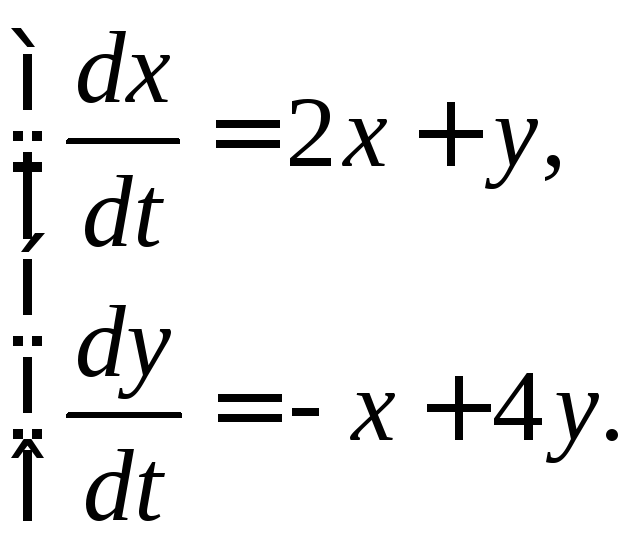 3.2.14.
3.2.14.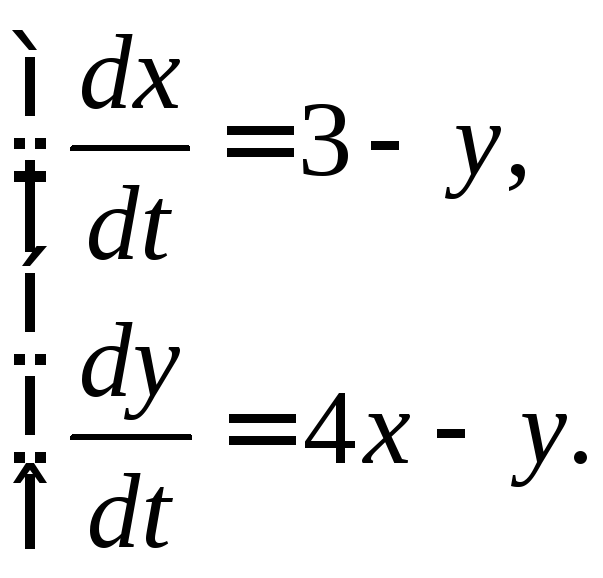
3.2.15.
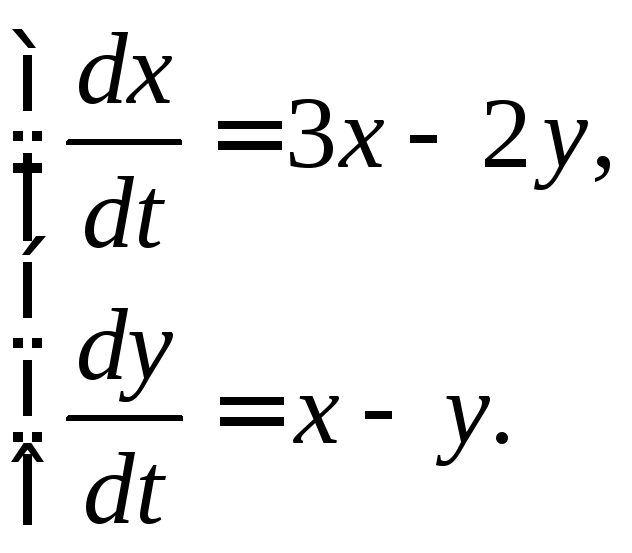 3.2.16.
3.2.16.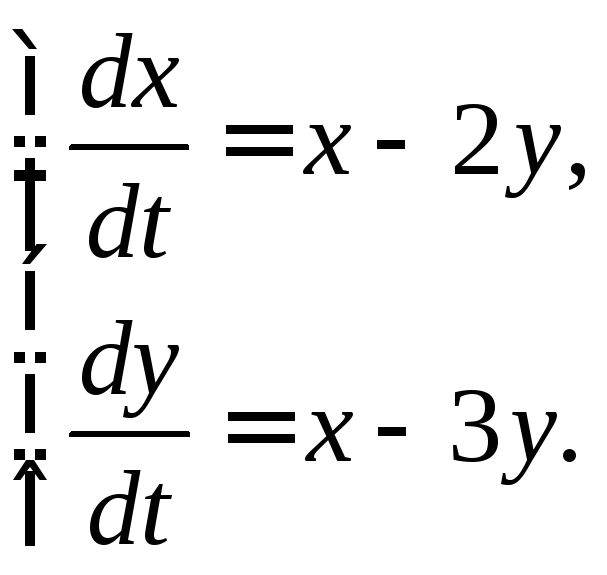
3.2.17.
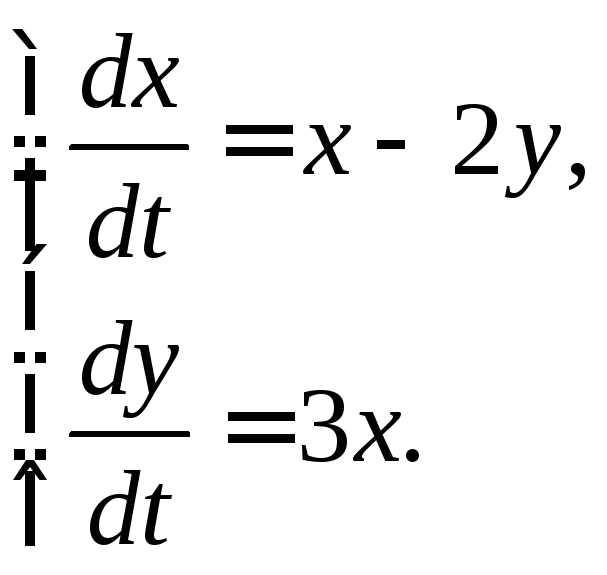 3.2.18.
3.2.18.
3.2.19.
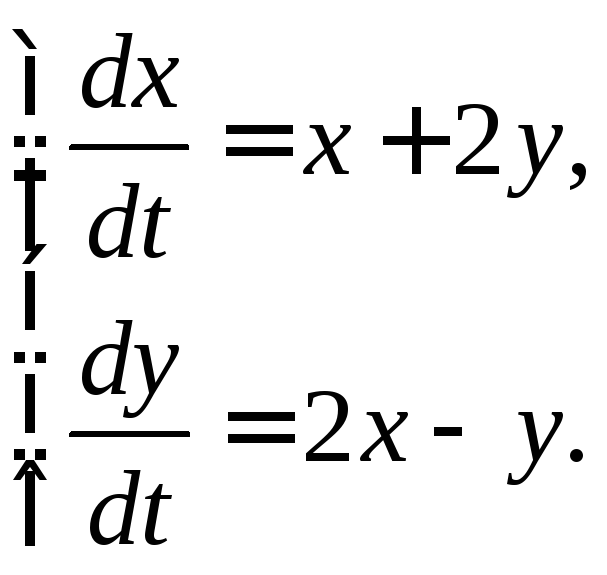 3.2.20.
3.2.20.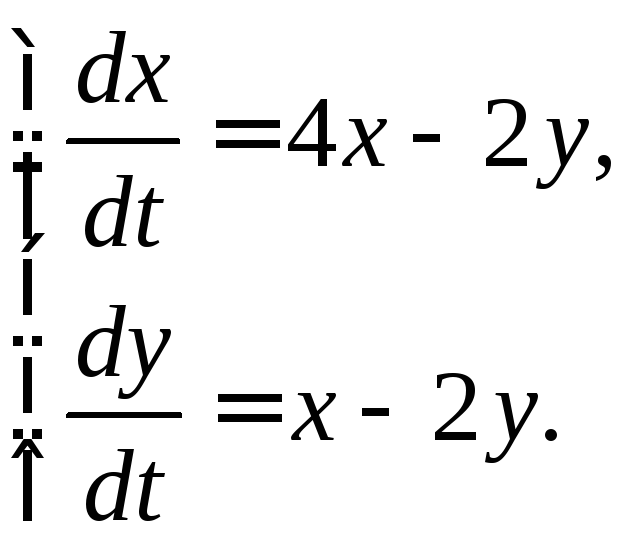
3.2.21.
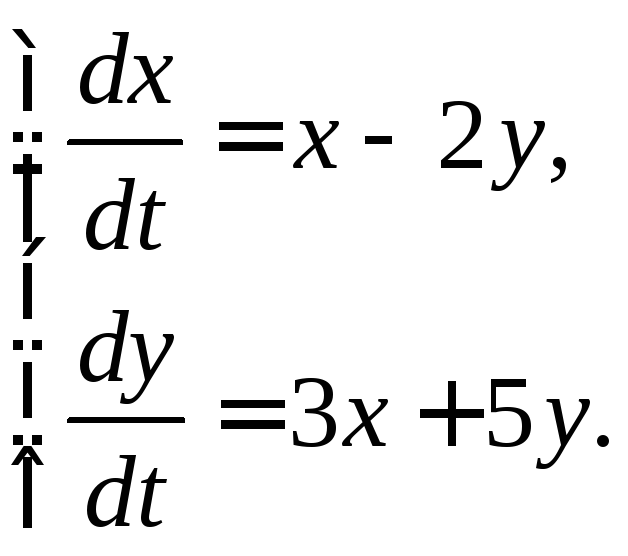 3.2.22.
3.2.22.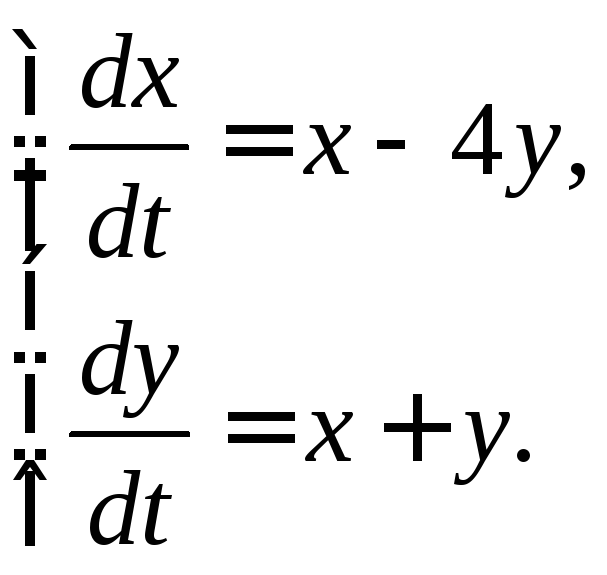
3.2.23.
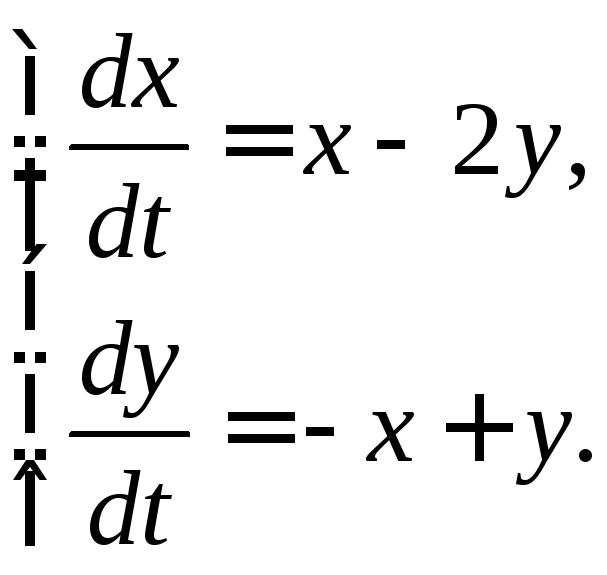 3.2.24.
3.2.24.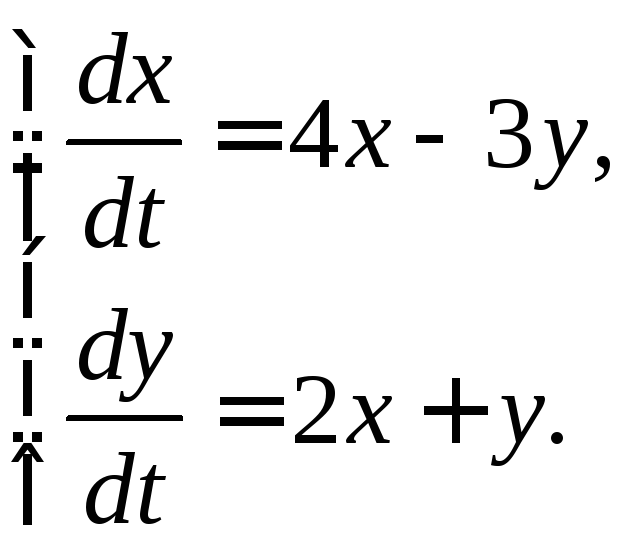
3.2.25.
 3.2.26.
3.2.26.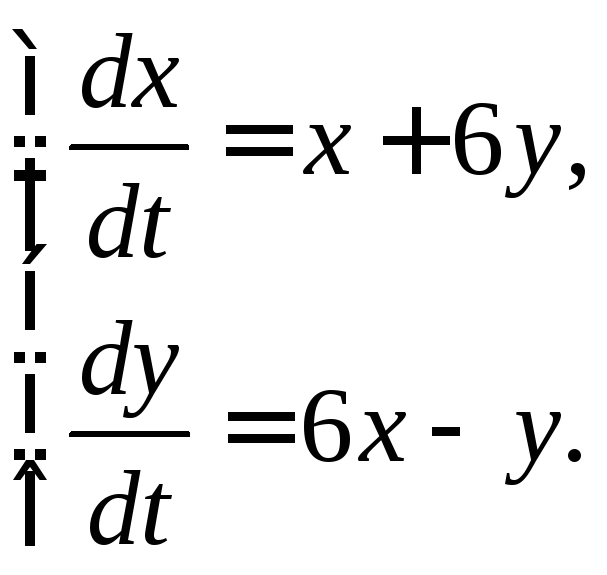
3.2.27.
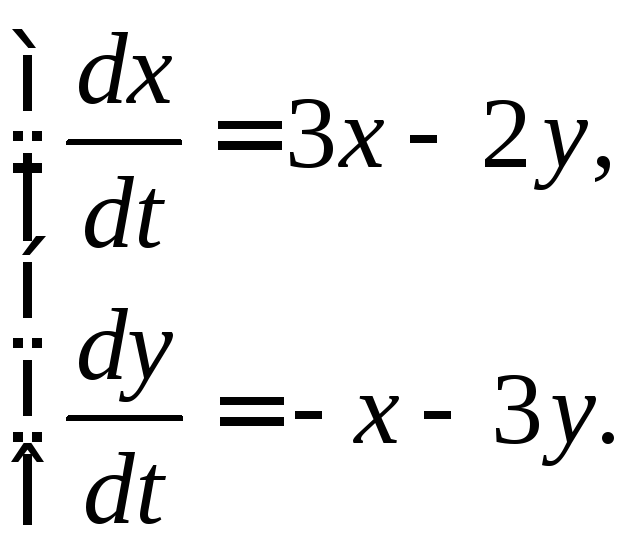 3.2.28.
3.2.28.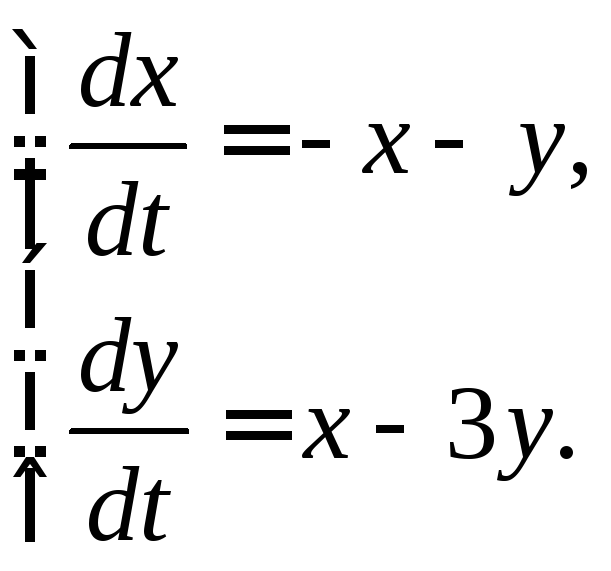
3.2.29.
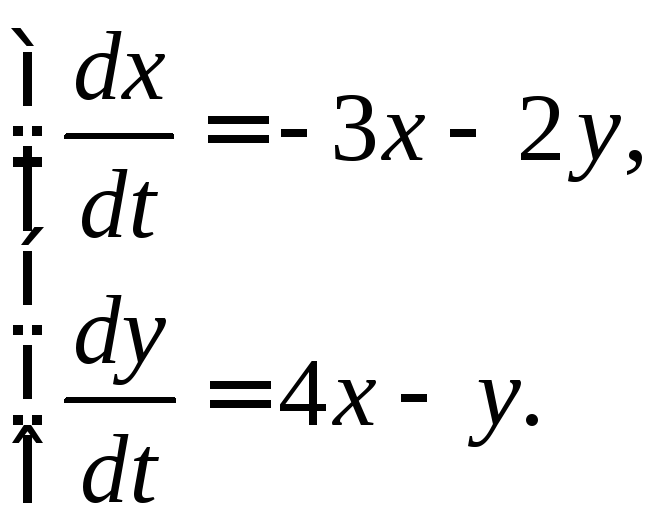 3.2.30.
3.2.30.
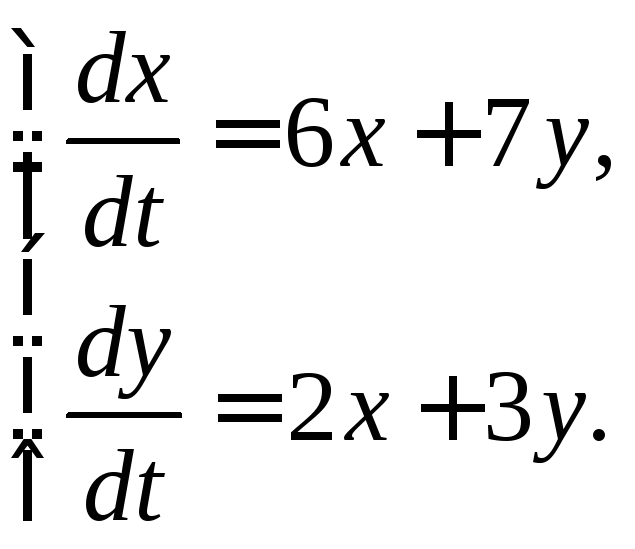
3.3. Линейные неоднородные системы дифференциальных уравнений с постоянными коэффициентами
Пусть задана неоднородная система линейных дифференциальных уравнений. Если найдена фундаментальная система решений соответствующей однородной системы, то решение неоднородной системы может быть найдено методом вариации произвольных постоянных.
Пример 3.4. Решить линейную неоднородную систему двух уравнений методом вариации постоянных
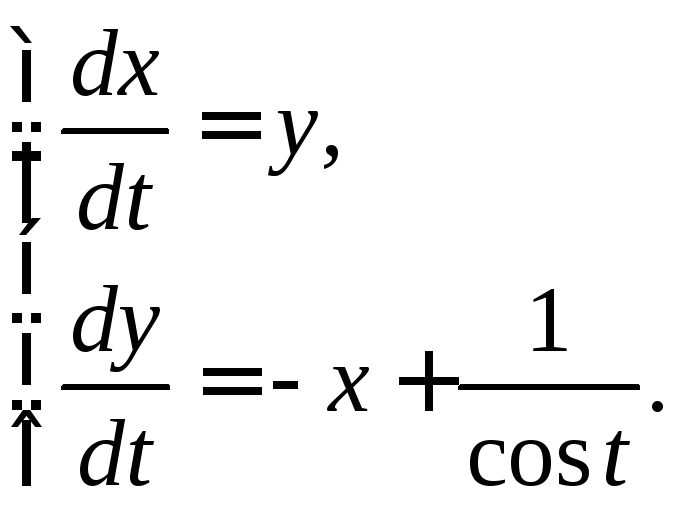 (3.8)
(3.8)
Решение.
1) Найдем сначала общее решение
соответствующей однородной системы
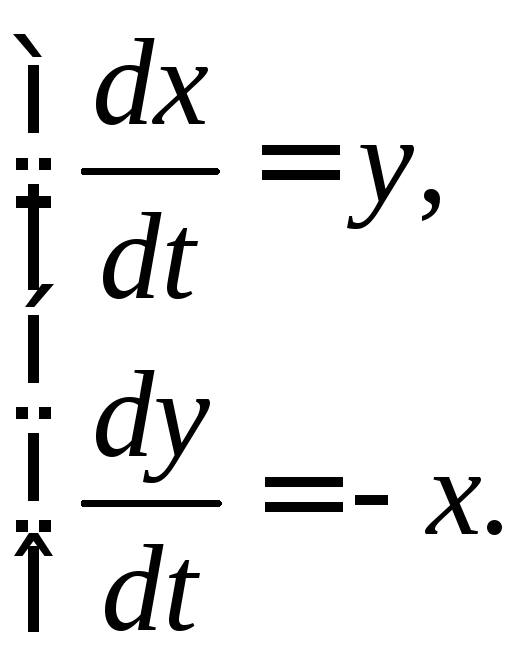 Составляем характеристическое уравнение
Составляем характеристическое уравнение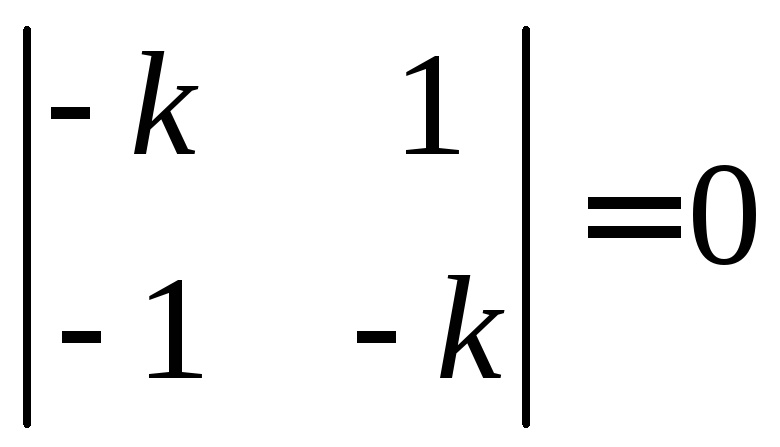 или
или![]() ,
находим его корни
,
находим его корни![]() .
.
2) В
случае комплексно-сопряженных корней
для системы с действительными
коэффициентами, два линейно-независимых
решения находят как действительную и
мнимую части комплексного вектора,
отвечающего одному из комплексных
корней. Запишем матричное уравнение
(см.3.7) для собственного числа
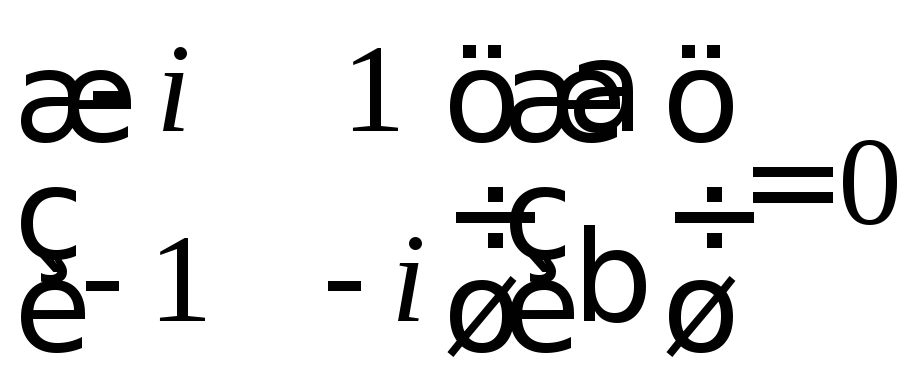 .
Откуда получаем связь между его
компонентами
.
Откуда получаем связь между его
компонентами![]() и комплексное фундаментальное решение
в векторном виде
и комплексное фундаментальное решение
в векторном виде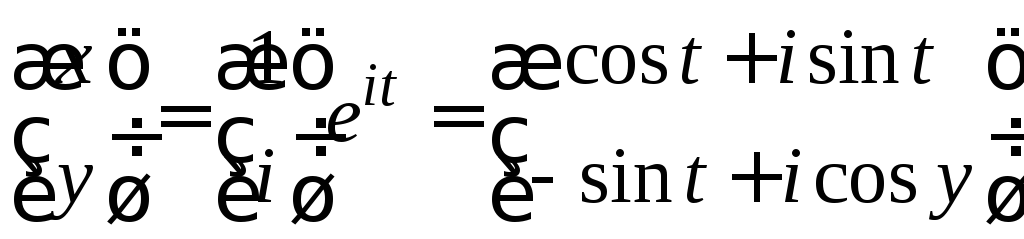 .
Тогда два действительных фундаментальных
решения
.
Тогда два действительных фундаментальных
решения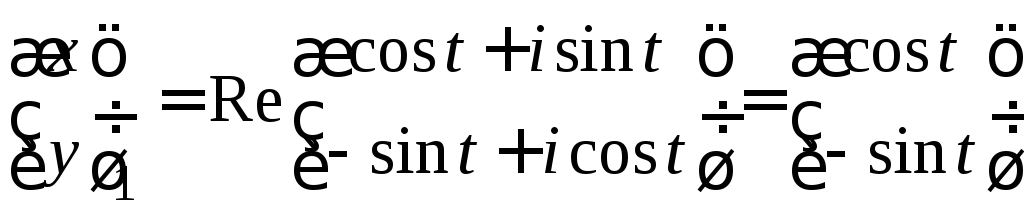 ,
,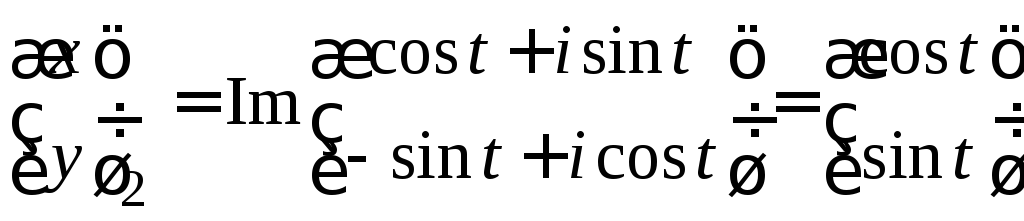 .
.
3) Следовательно, общее решение однородной системы
 .
.
4)
Общее решение неоднородной системы
ищем методом вариации произвольных
постоянных, то есть рассматриваем
параметры
![]() как функции переменной
как функции переменной![]()
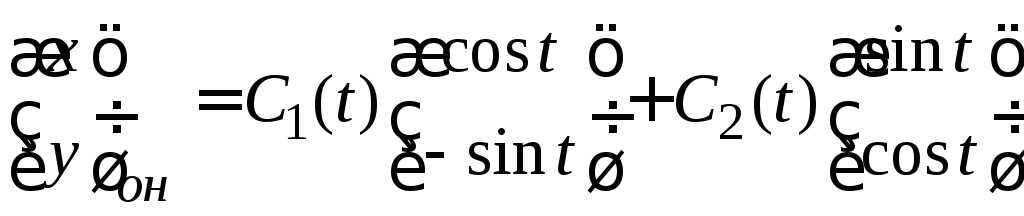 . (3.9)
. (3.9)
Подставляя
вектор (3.9) в (3.8), получим для нахождения
функций
![]() систему
систему
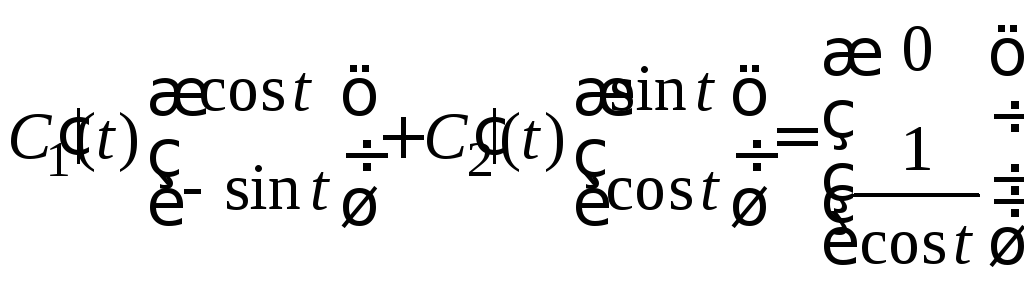 .
.
Эта система всегда разрешима, т.к. ее определитель есть определитель Вронского для двух линейно-независимых векторных решений и, следовательно, не равен нулю ни при каком значении независимой переменной.
5) Решаем систему по правилу Крамера
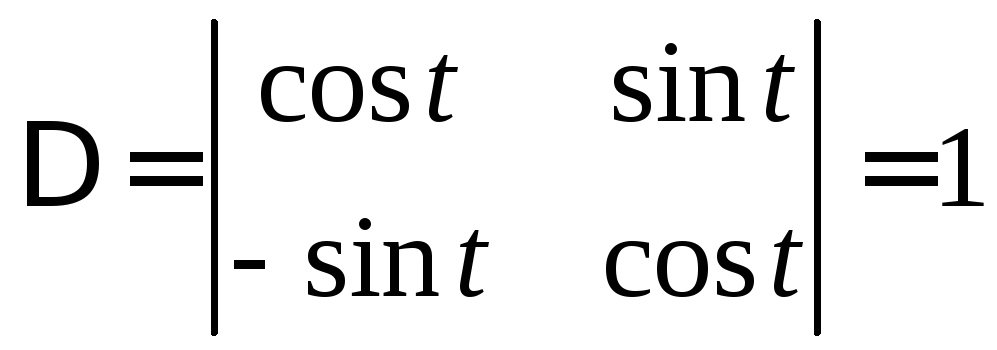 ,
,
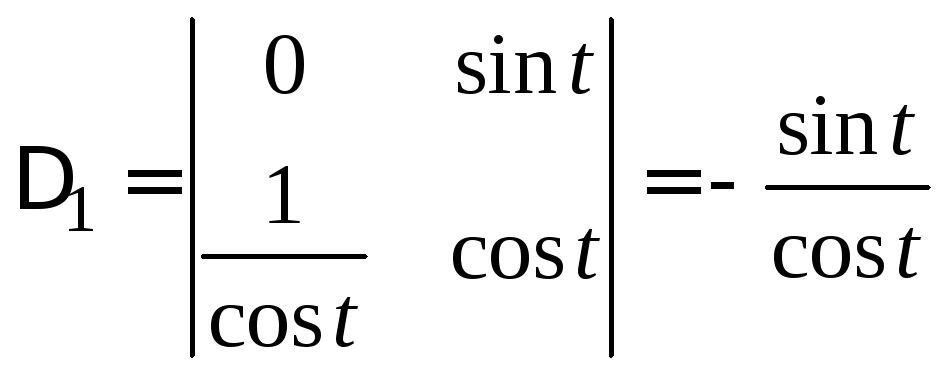 ,
,
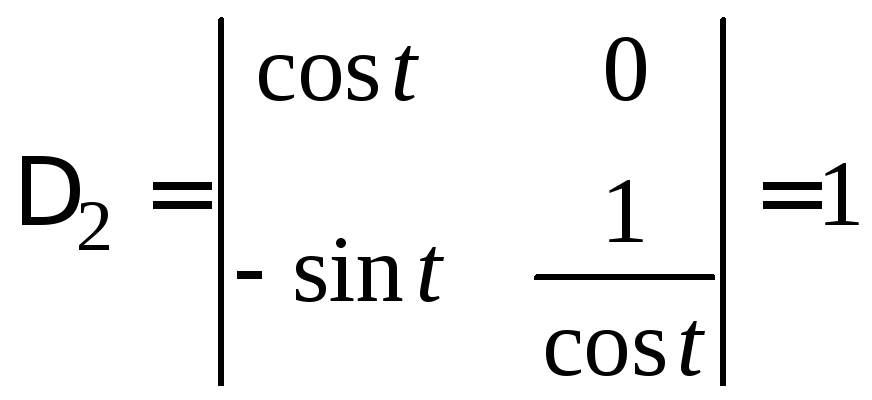 ,
,
![]() .
.
Интегрируя, получаем
![]() .
.
Таким образом,
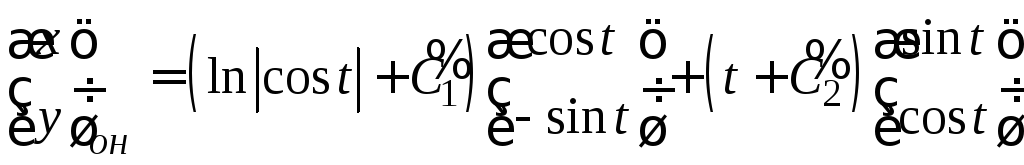 ,
,
где
![]() - произвольные постоянные.
- произвольные постоянные.
Ответ.
![]() ,
,![]() .
.
Система
неоднородных уравнений может быть также
решена сведением к одному дифференциальному
уравнению относительно неизвестной
функции. Если в неоднородной системе
 вектор функция
вектор функция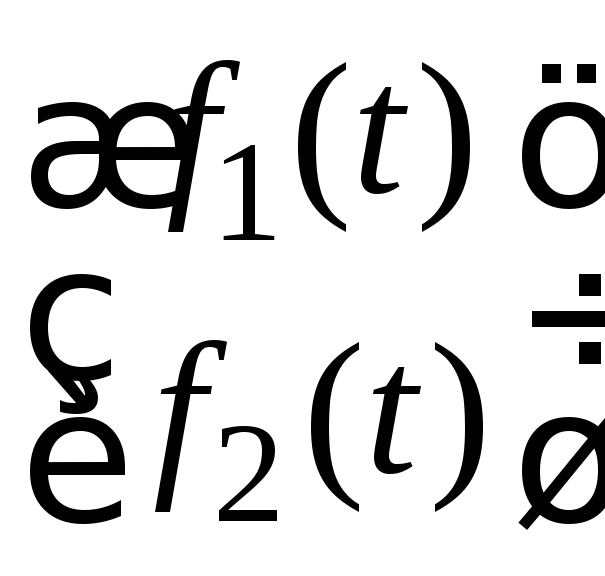 имеет вид
имеет вид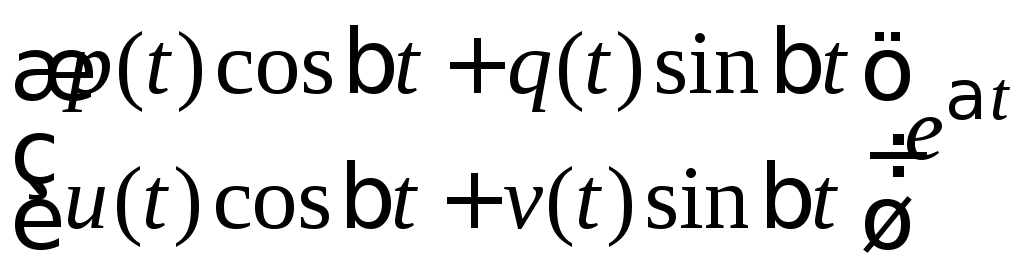 ,
то может быть использован метод
неопределенных коэффициентов для
нахождения частного решения системы.
,
то может быть использован метод
неопределенных коэффициентов для
нахождения частного решения системы.
Задание 3.3. Решить системы.
3.3.1. 3.3.2.
3.3.3.
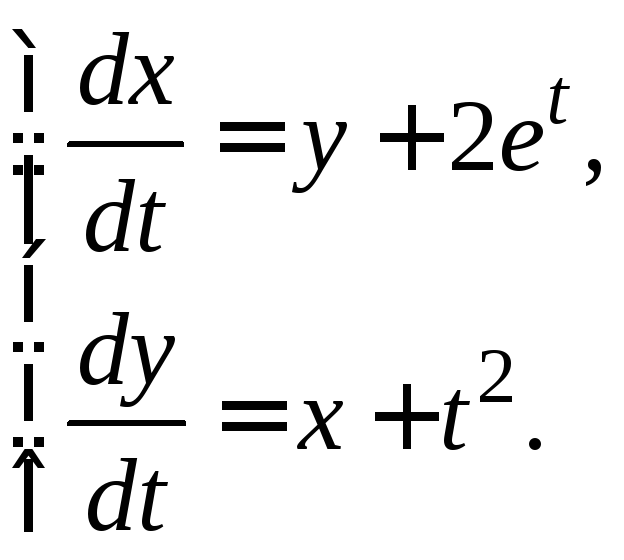 3.3.4.
3.3.4.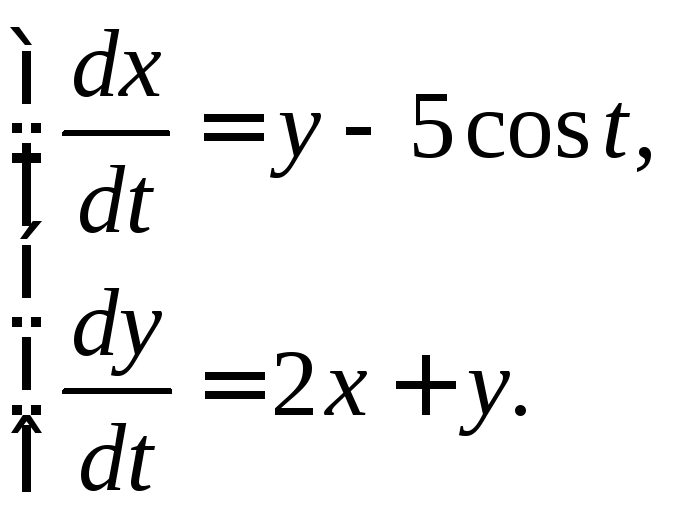
3.3.5.
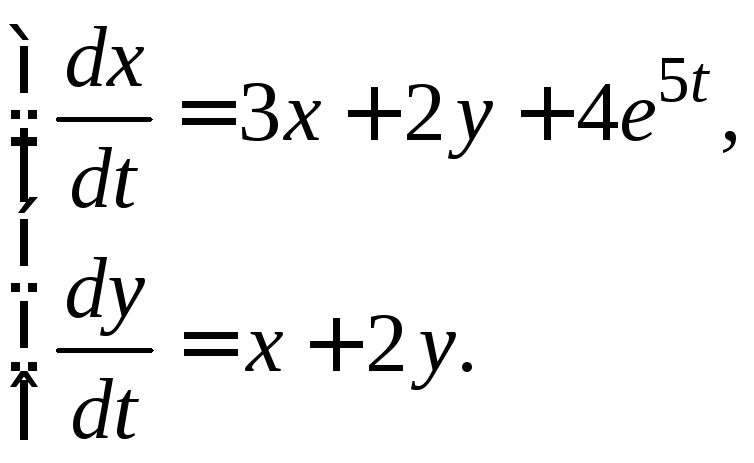 3.3.6.
3.3.6.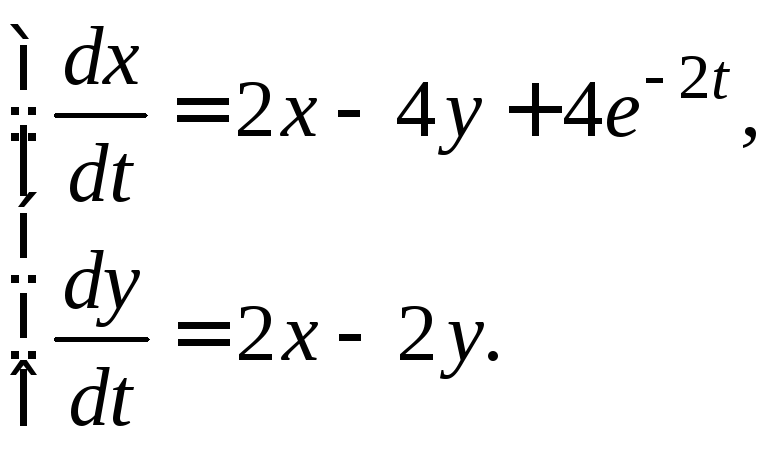
3.3.7.
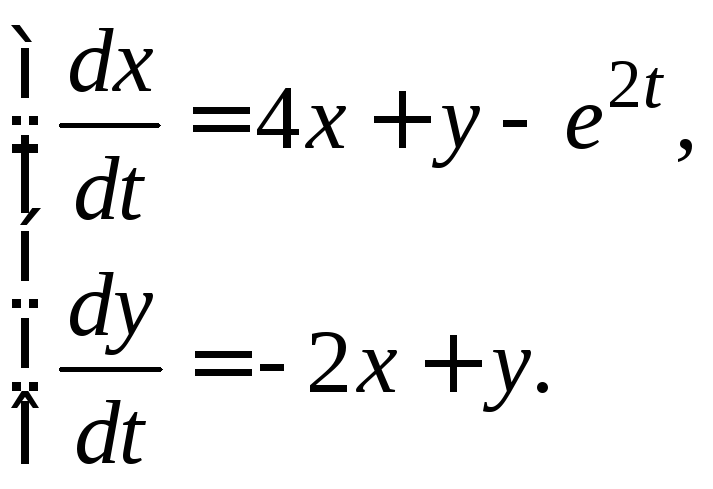 3.3.8.
3.3.8.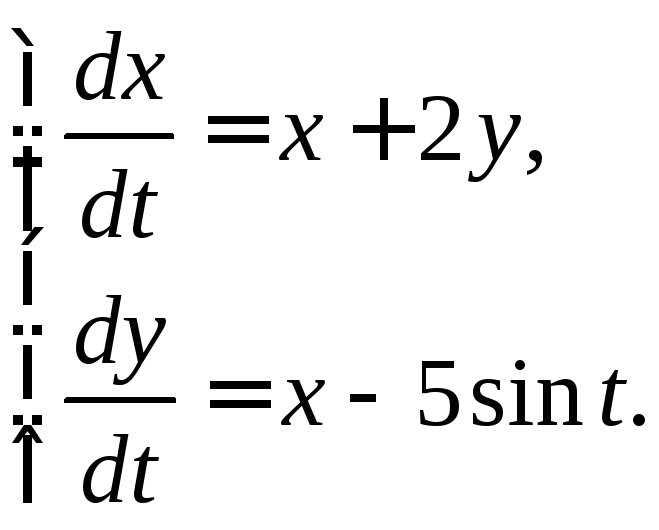
3.3.9.
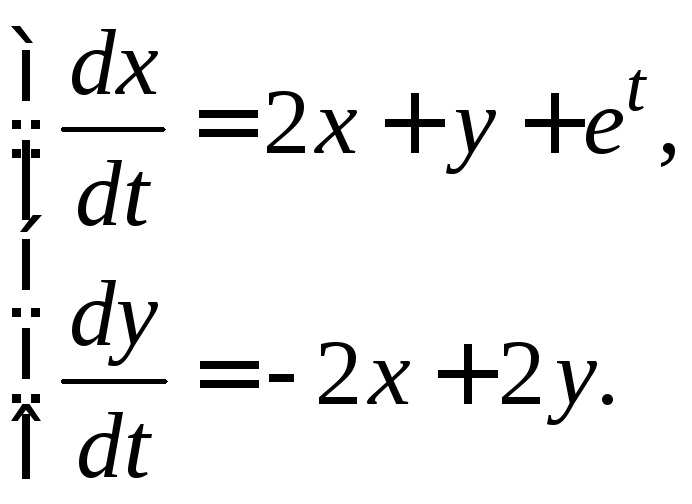 3.3.10.
3.3.10.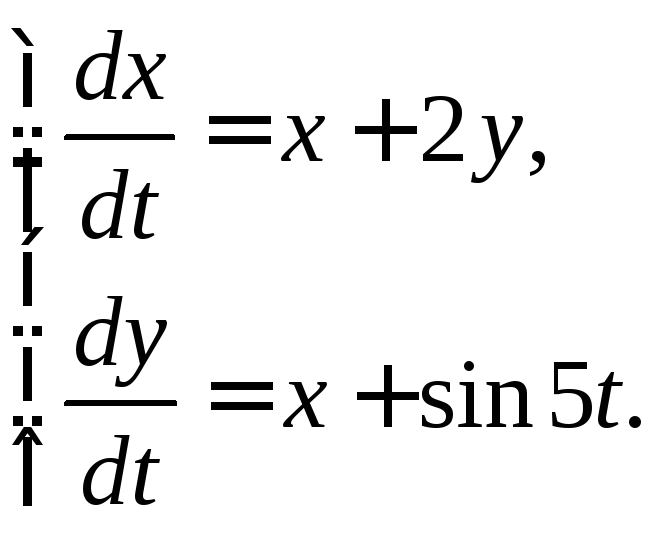
3.3.11.
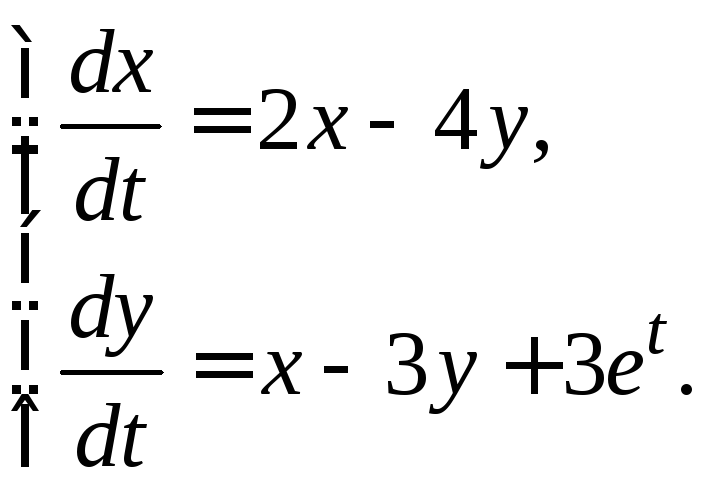 3.3.12.
3.3.12.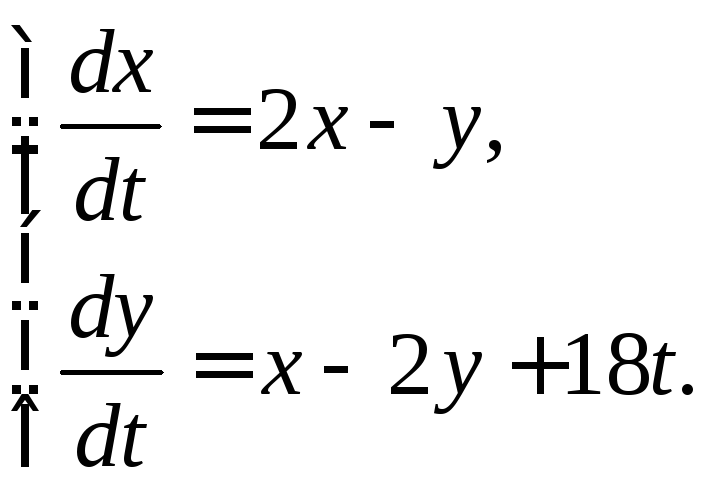
3.3.13.
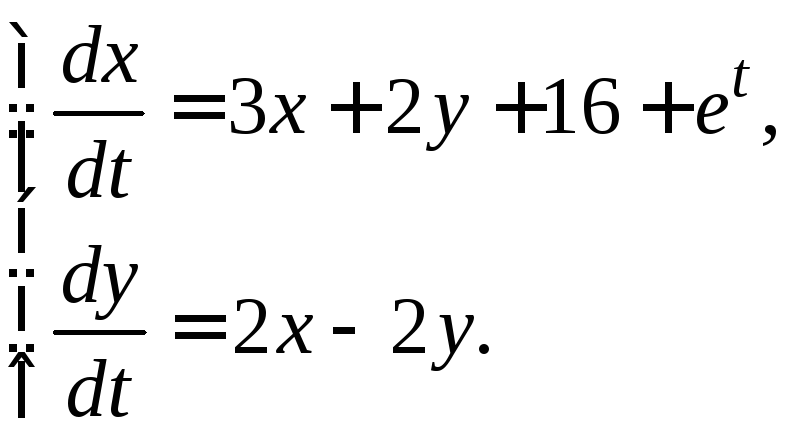 3.3.14.
3.3.14.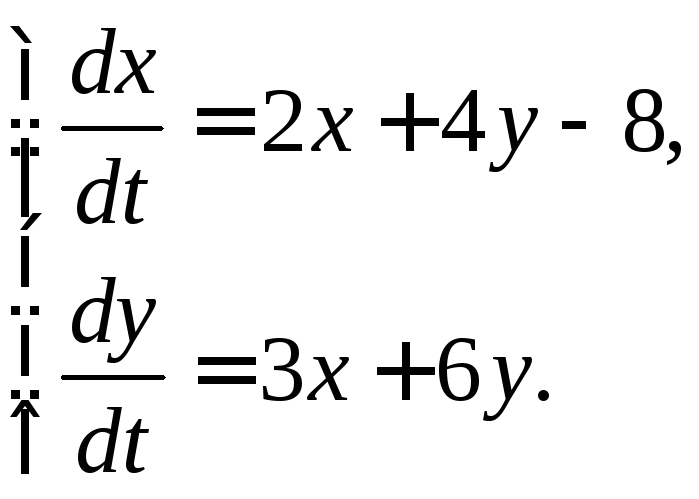
3.3.15.
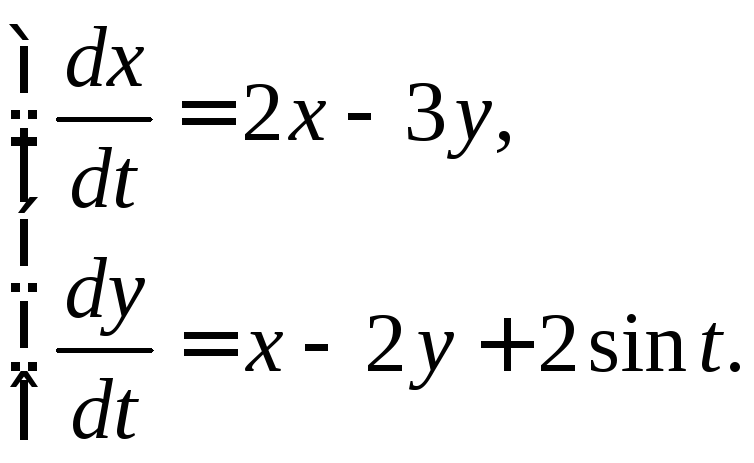 3.3.16.
3.3.16.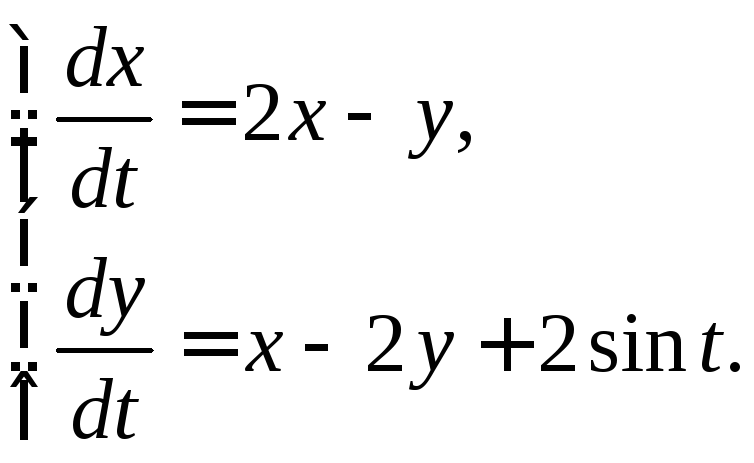
3.3.17.
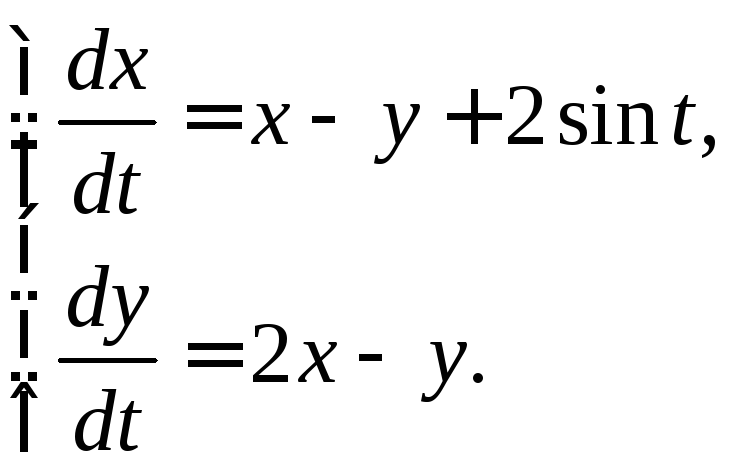 3.3.18.
3.3.18.
3.3.19.
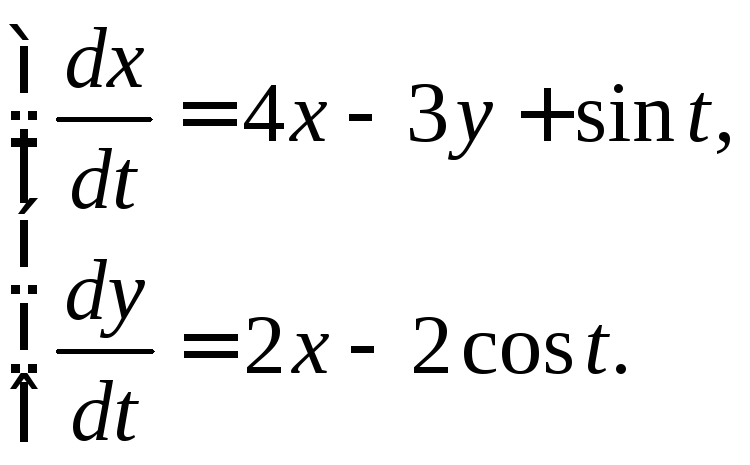 3.3.20.
3.3.20.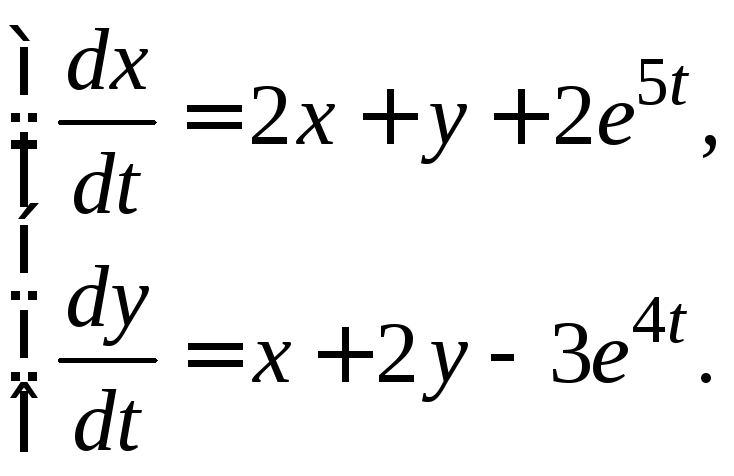
3.3.21.
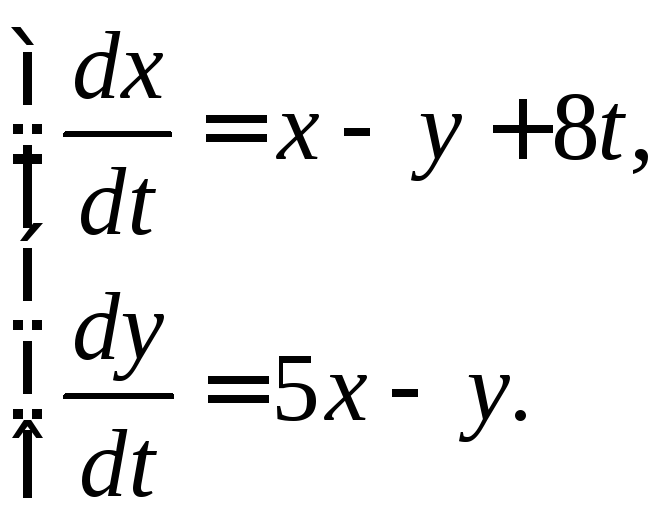 3.3.22.
3.3.22.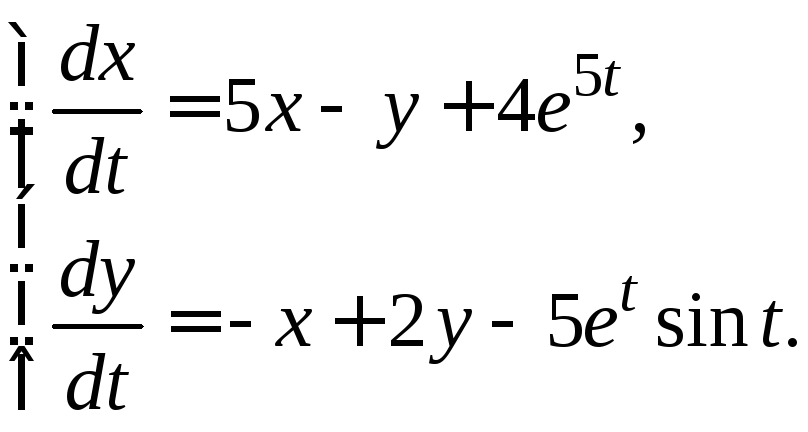
3.3.23.
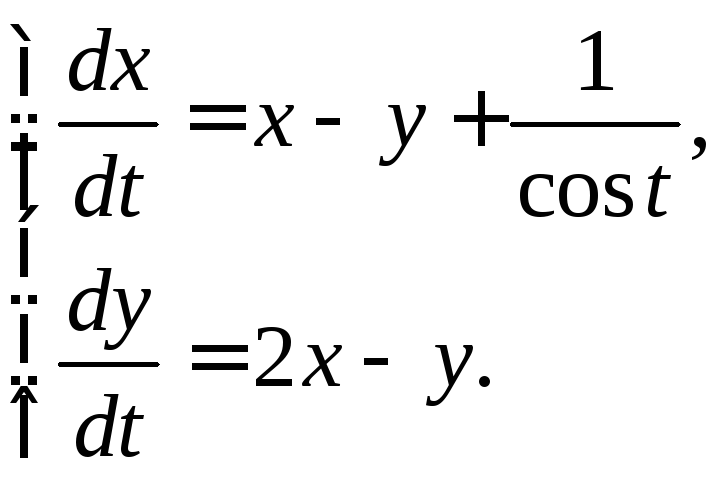 3.3.24.
3.3.24.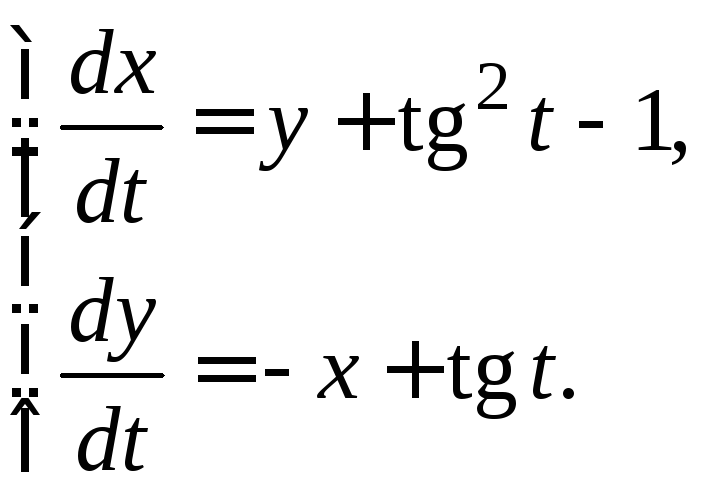
3.3.25.
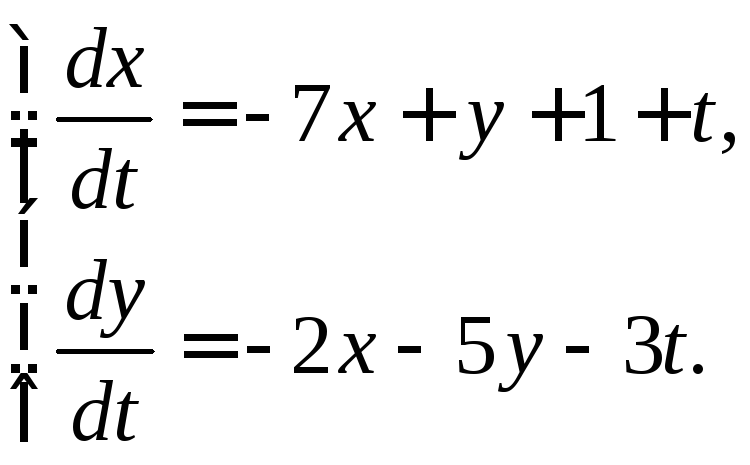 3.3.26.
3.3.26.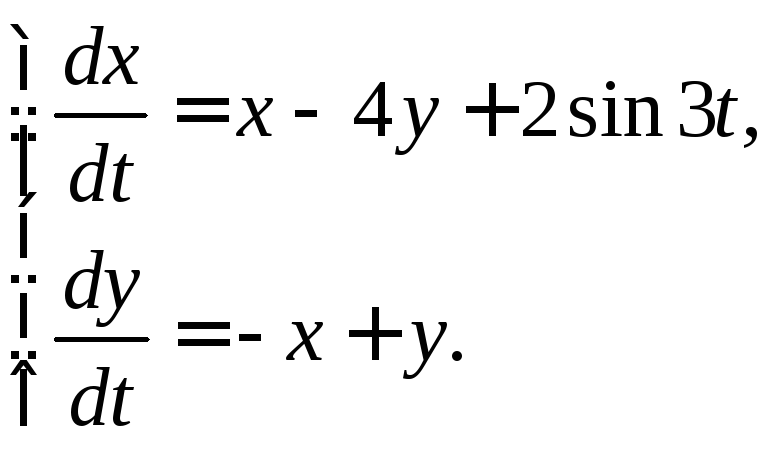
3.3.27.
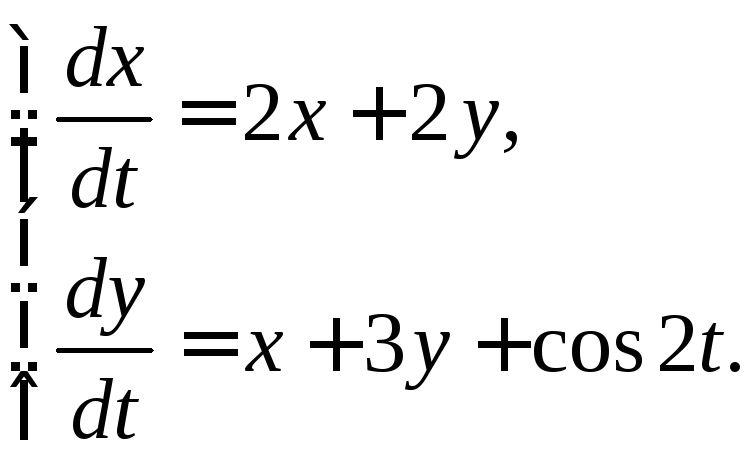 3.3.28.
3.3.28.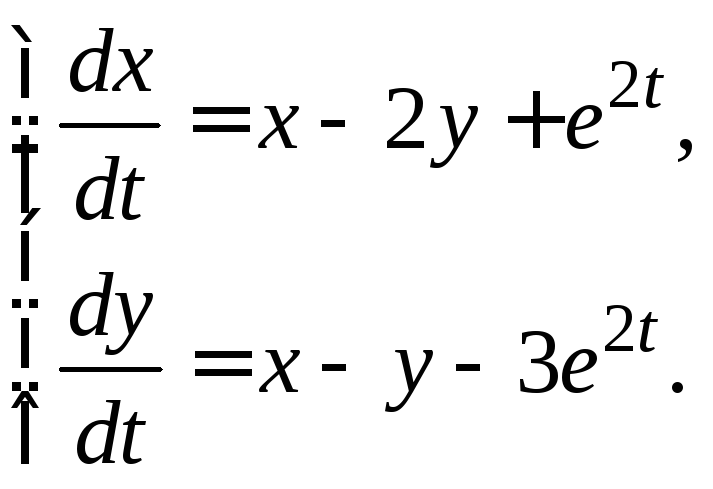
3.3.29.
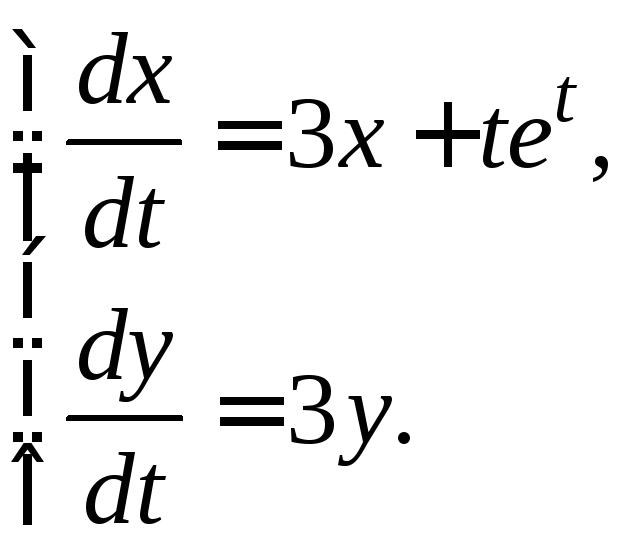 3.3.30.
3.3.30.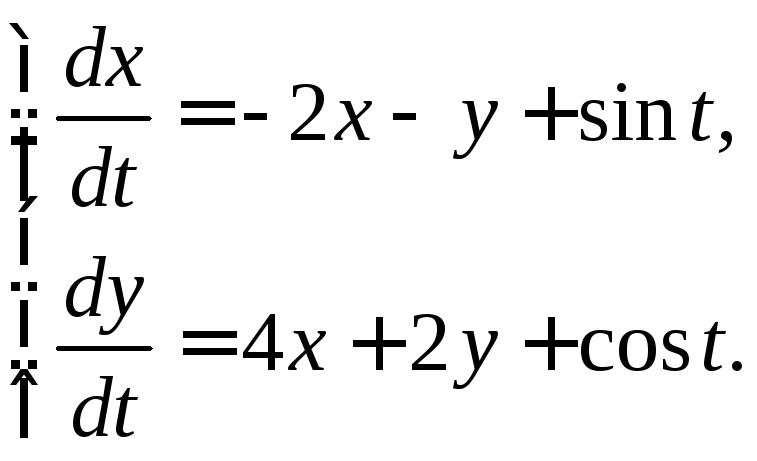
3.4. Исследование на устойчивость однородной линейной системы дифференциальных уравнений
При использовании дифференциальных уравнений или систем дифференциальных уравнений важным является наличие устойчивости решений: малые изменения начальных условий должны вызывать малые изменения решений. Для дифференциальных уравнений и систем первого порядка исследование на устойчивость решения сводится к исследованию на устойчивость тривиального решения (точки покоя). В случае однородных линейных систем с постоянными коэффициентами устойчивость точки покоя и ее тип определяется значениями корней характеристического уравнения.
Пример
3.5.
Исследовать на устойчивость и определить
тип точки покоя системы
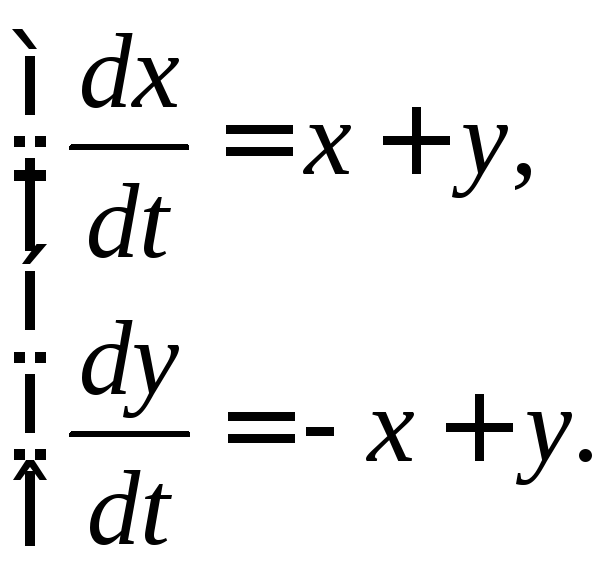
Решение.
1) Составляем характеристическое
уравнение
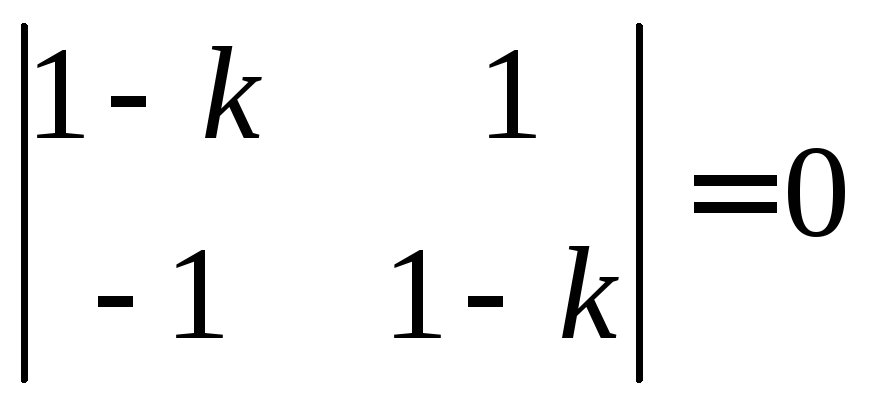 .
.
2) Находим
его корни
![]() .
.
3) Вычисляем
действительные части корней
![]() .
.
4) Так как действительная часть больше нуля, то точка покоя является неустойчивой, ее тип – неустойчивый фокус.
Ответ. Неустойчива, неустойчивый фокус.
Задание 3.4. Исследовать на устойчивость и определить тип точки покоя систем.
