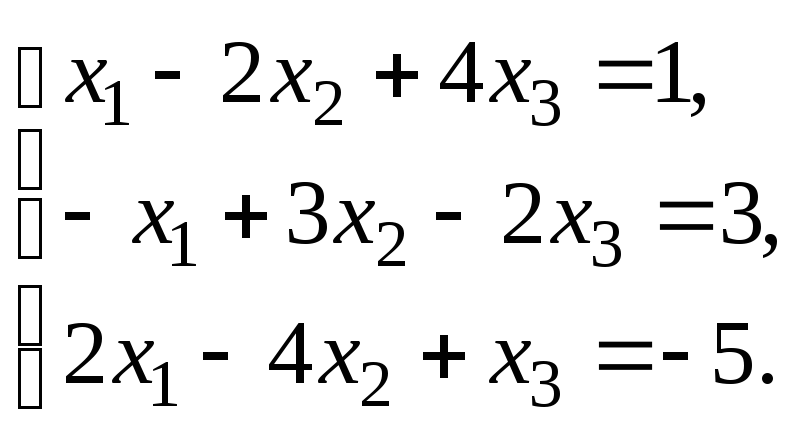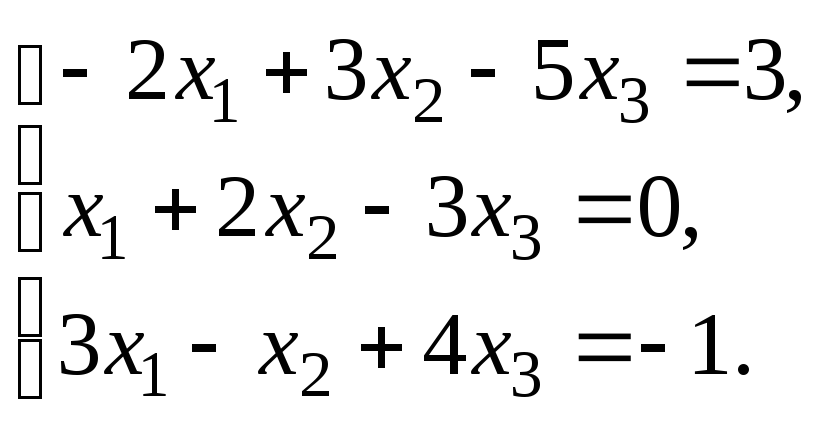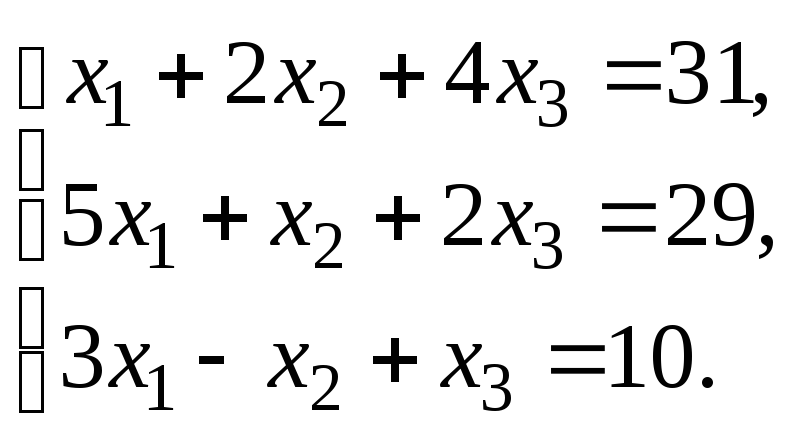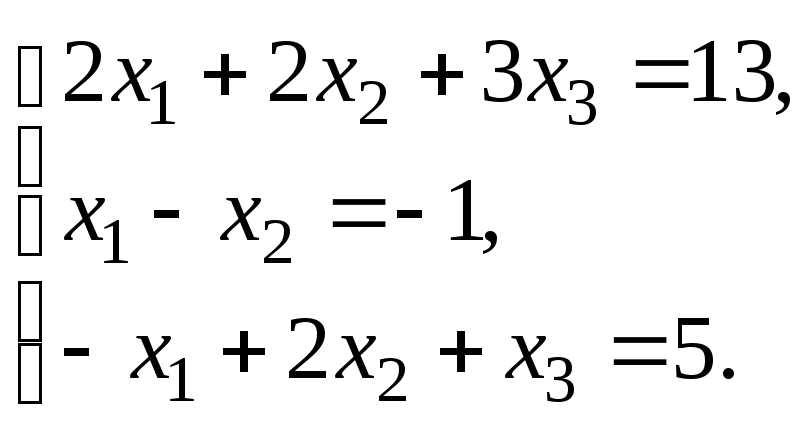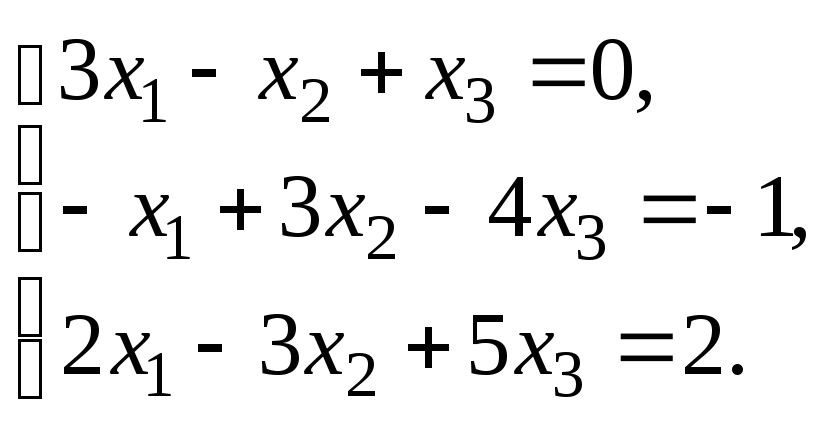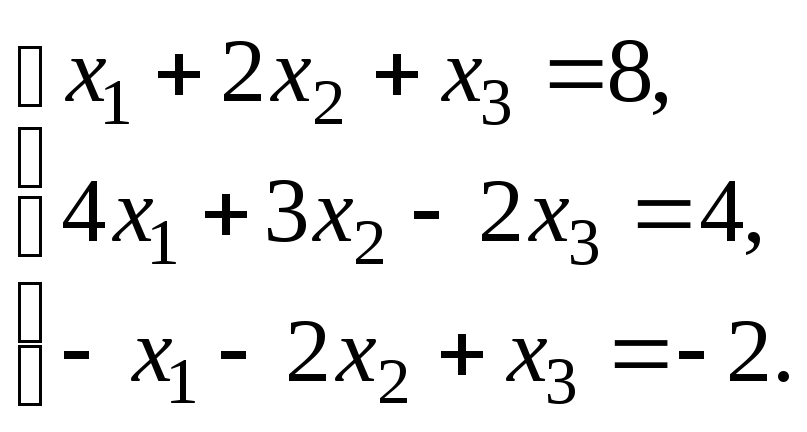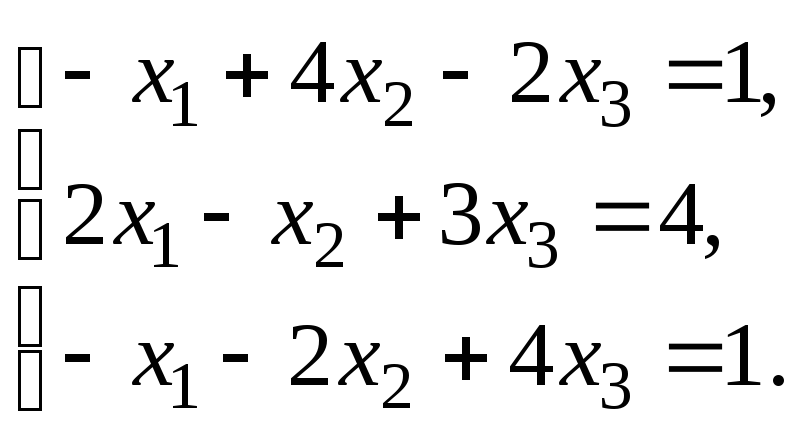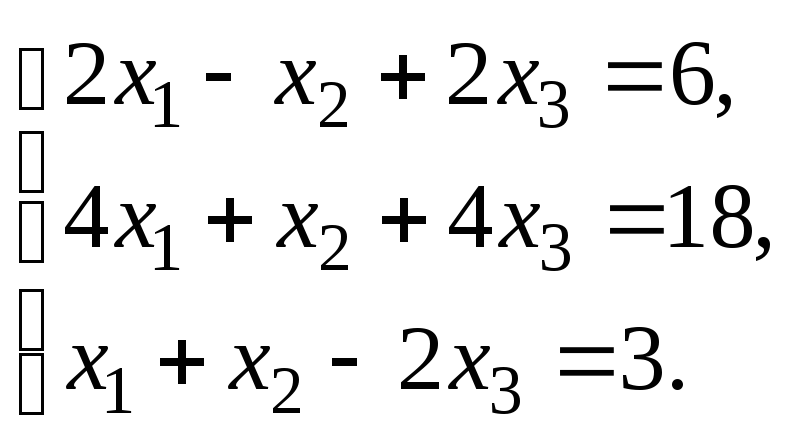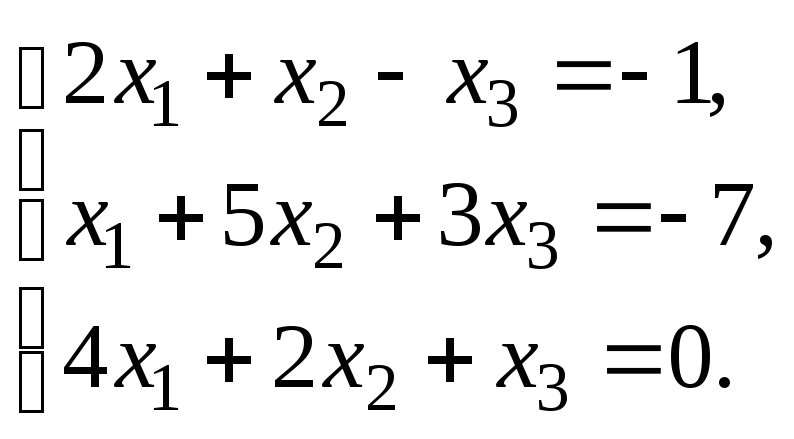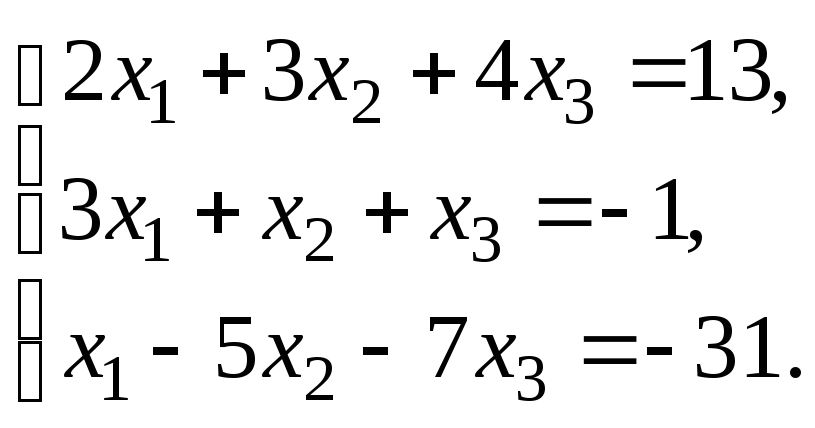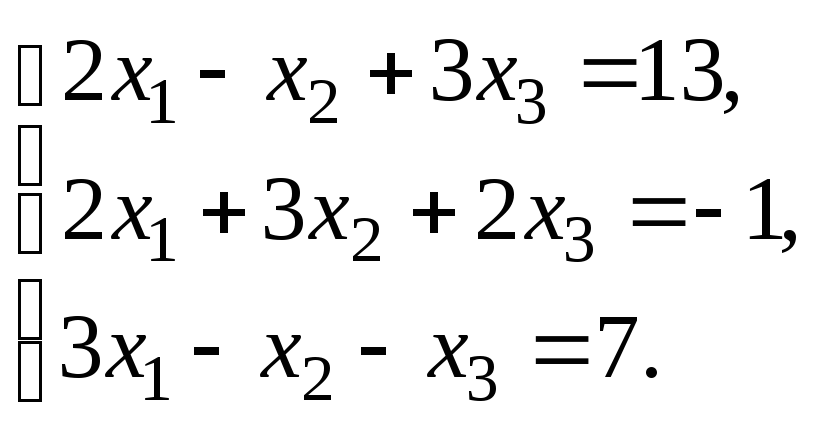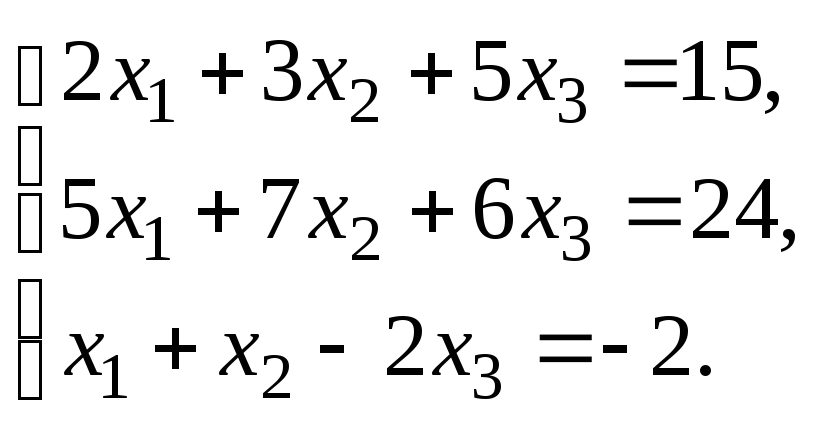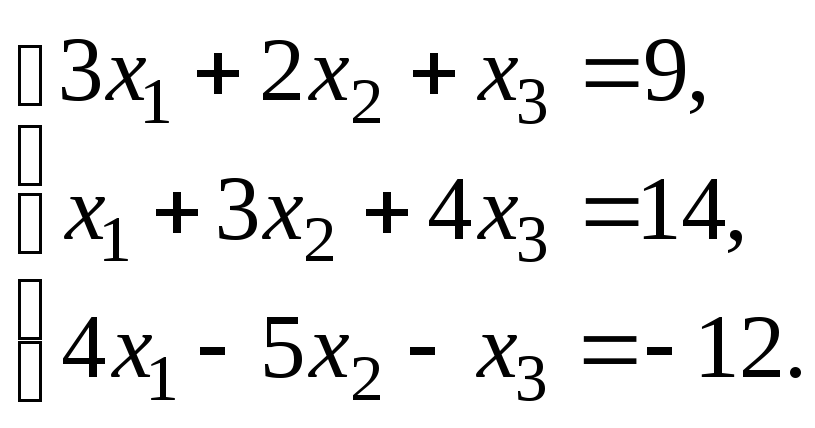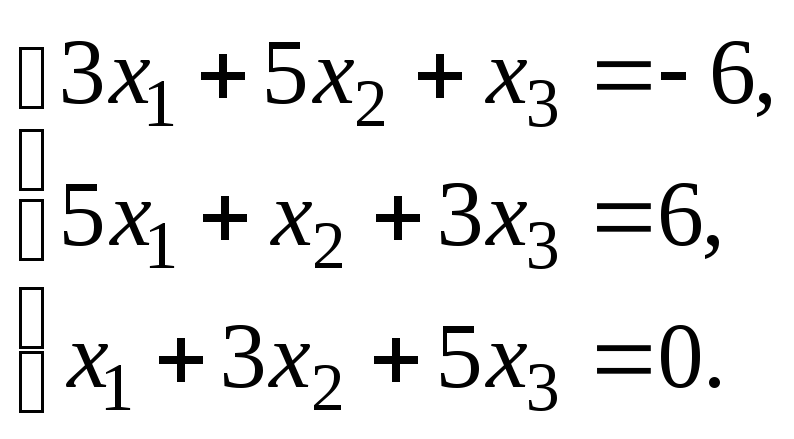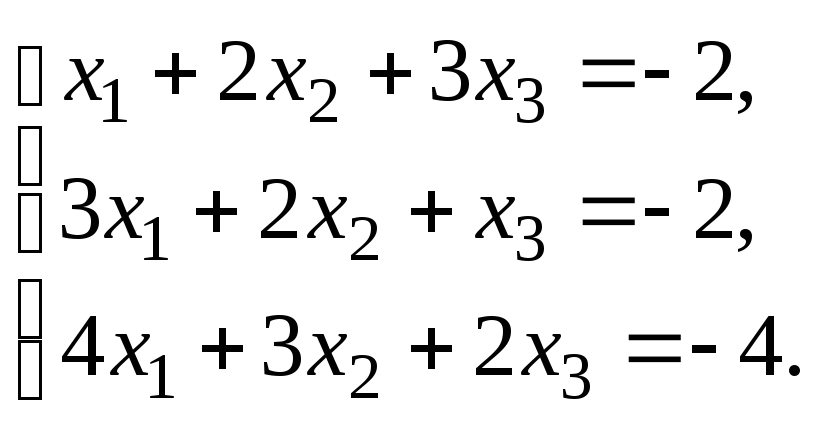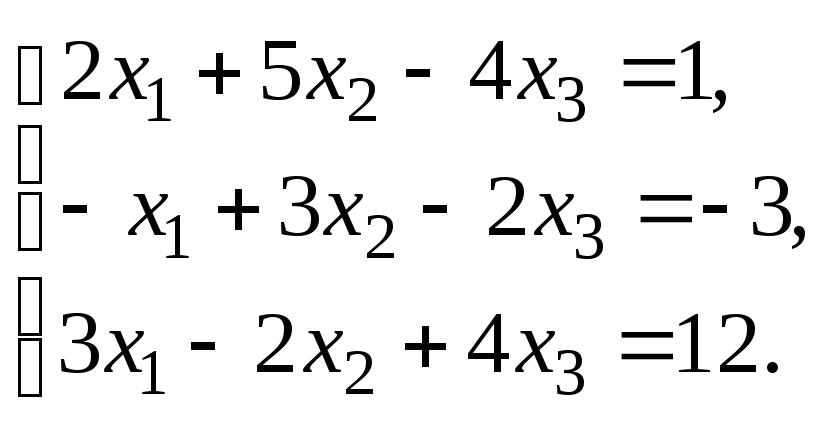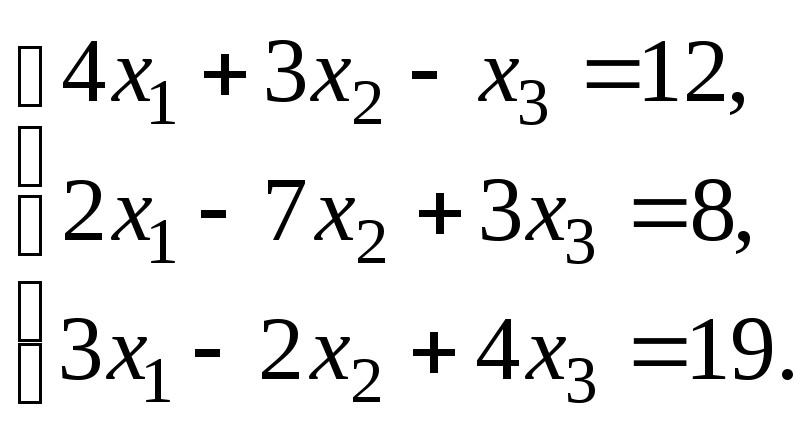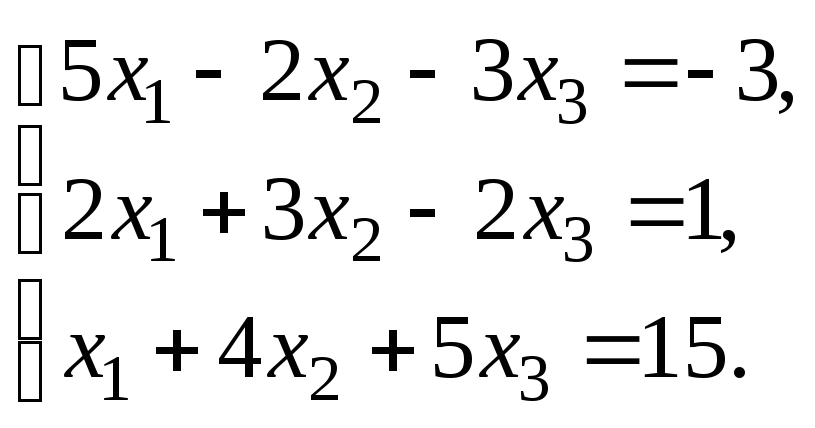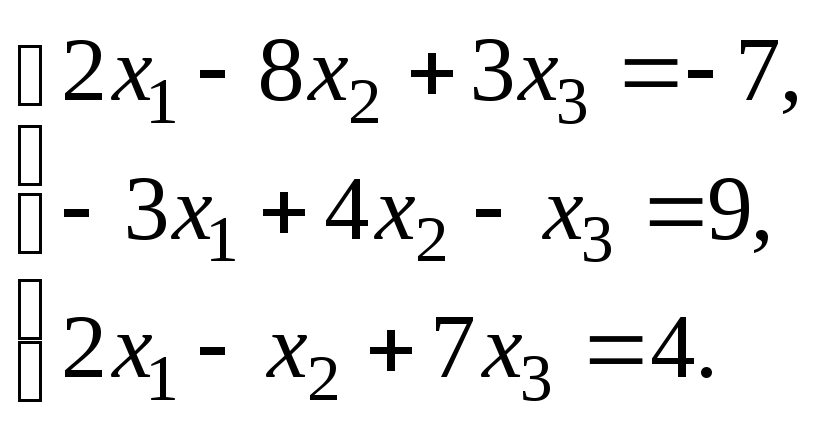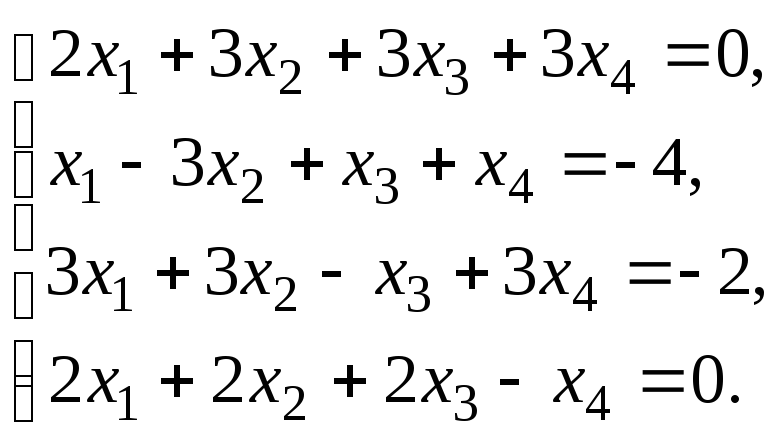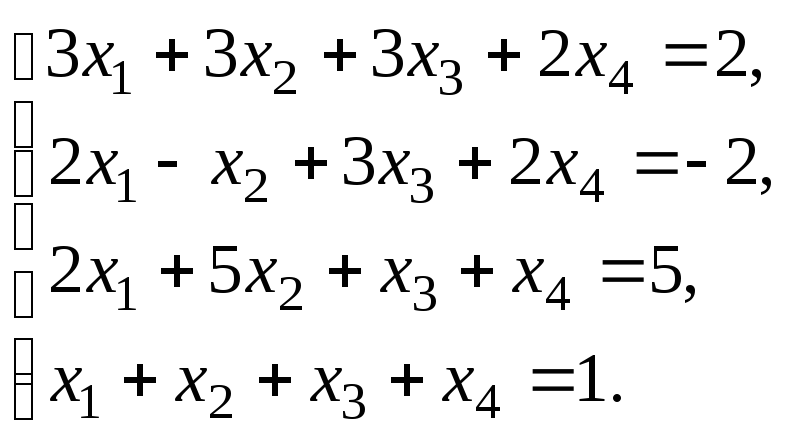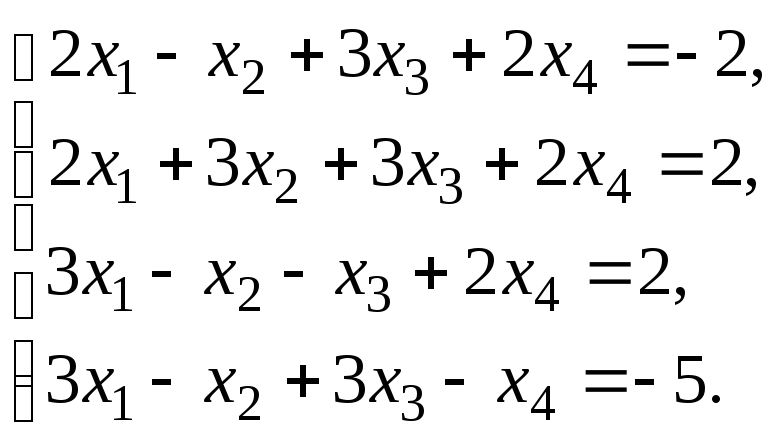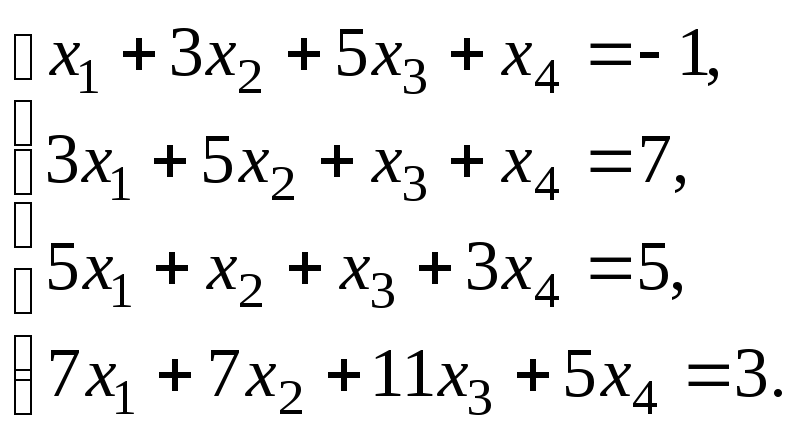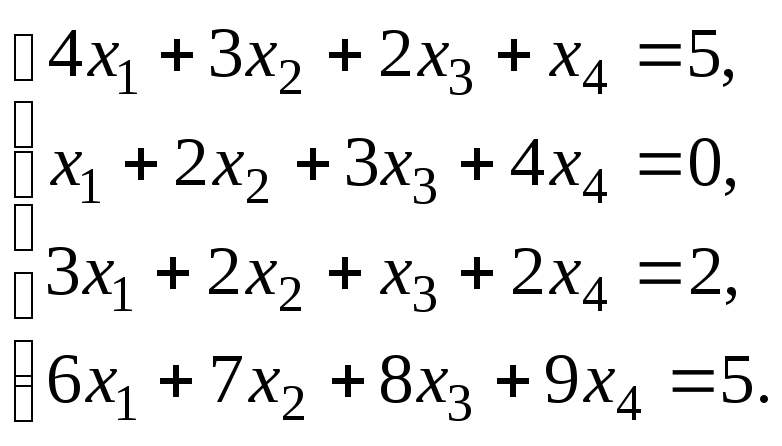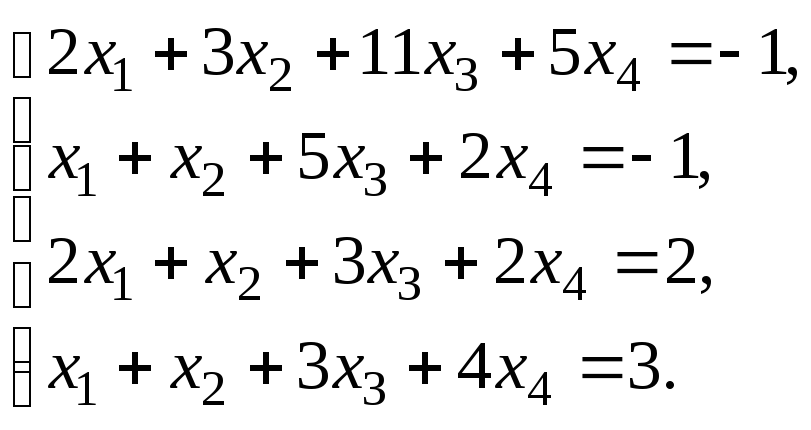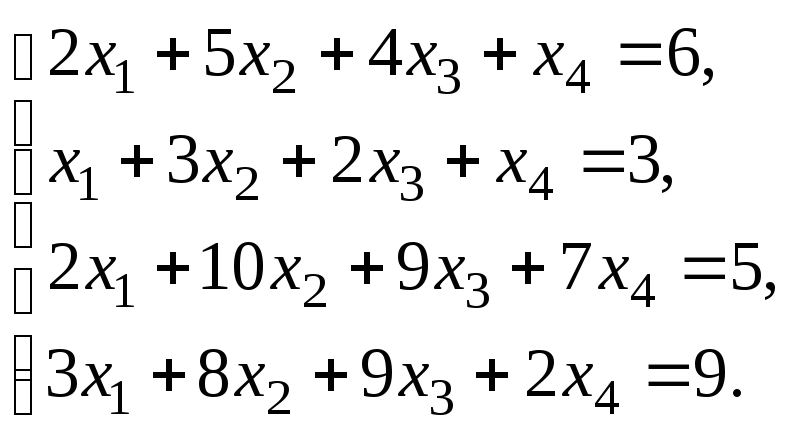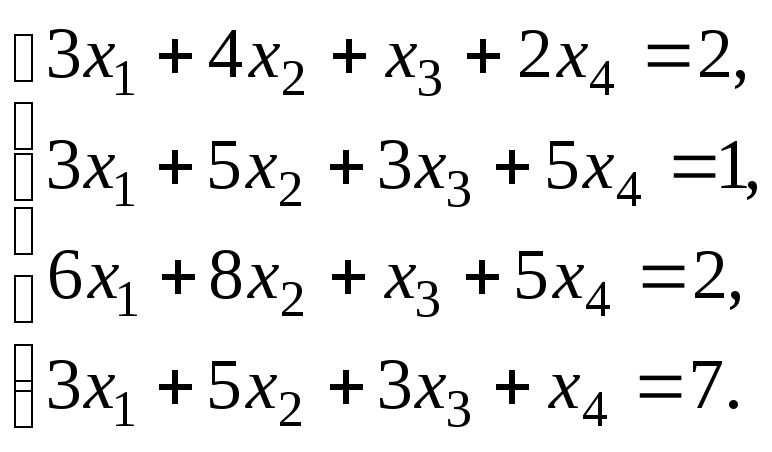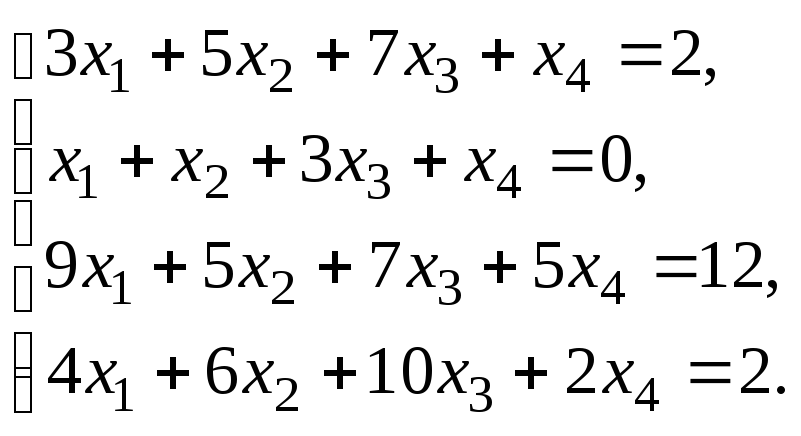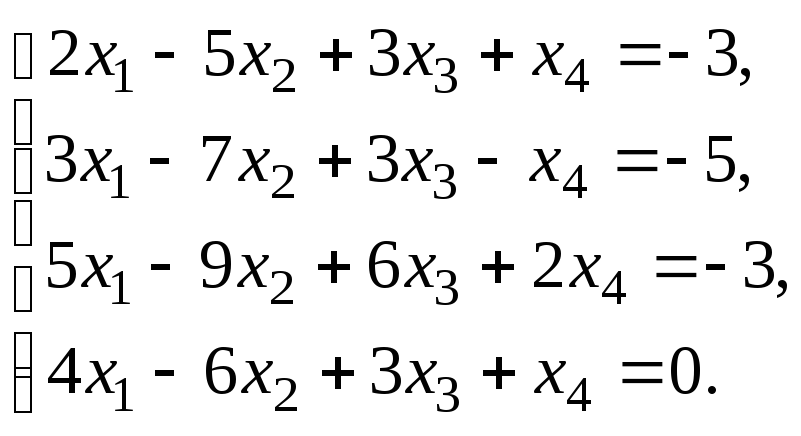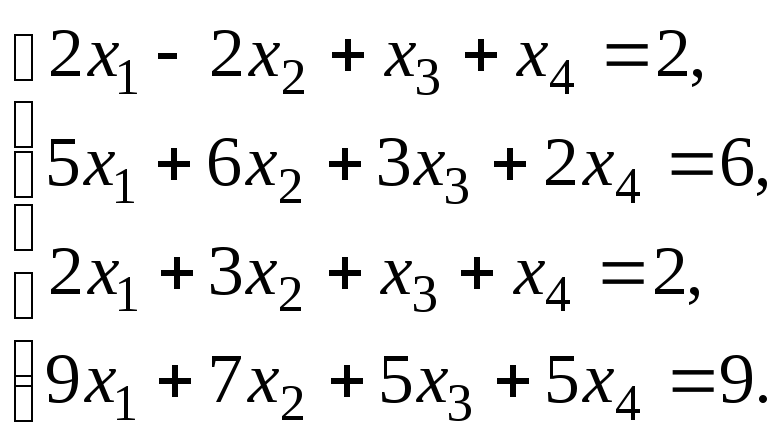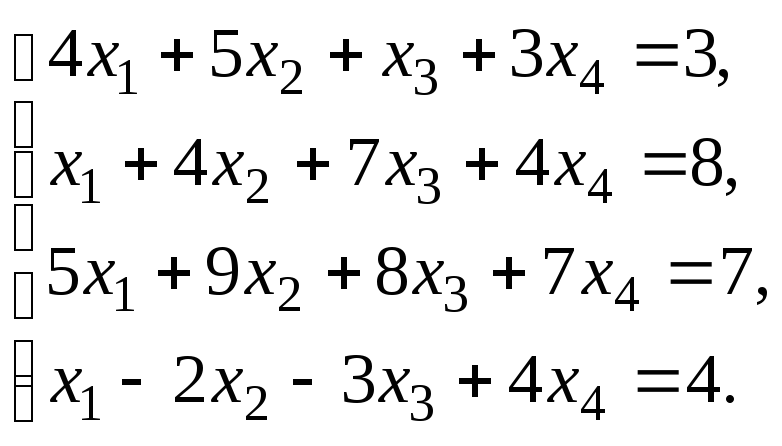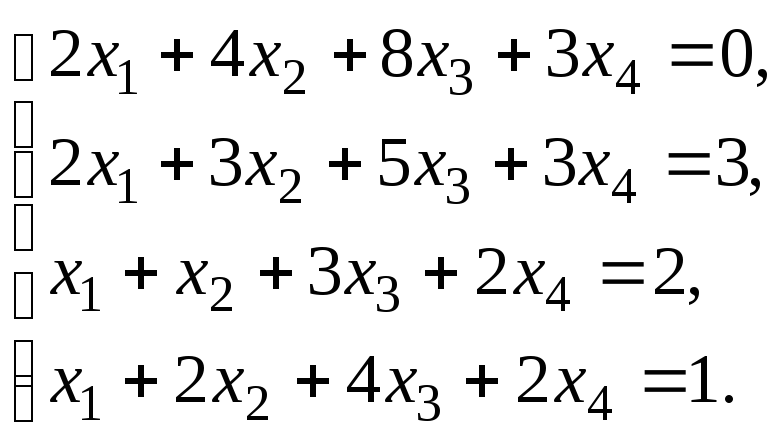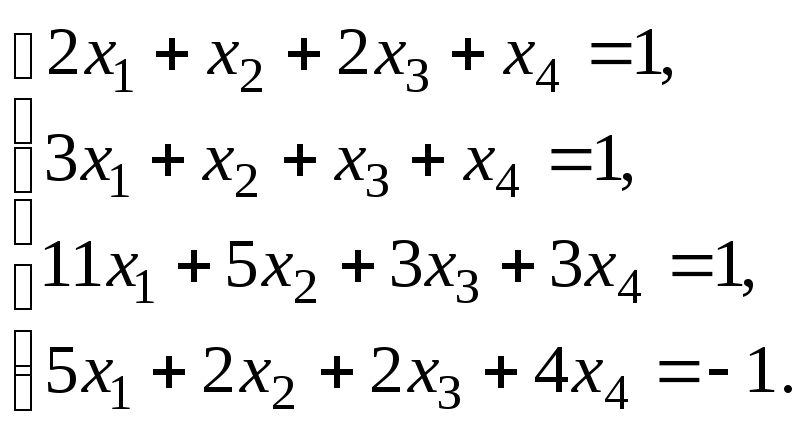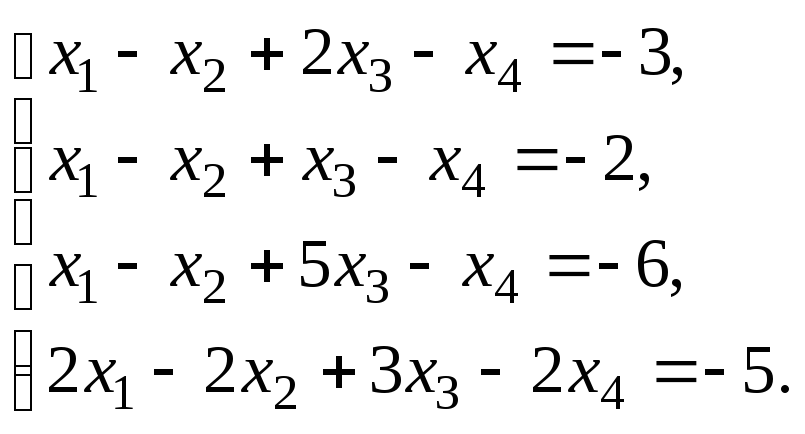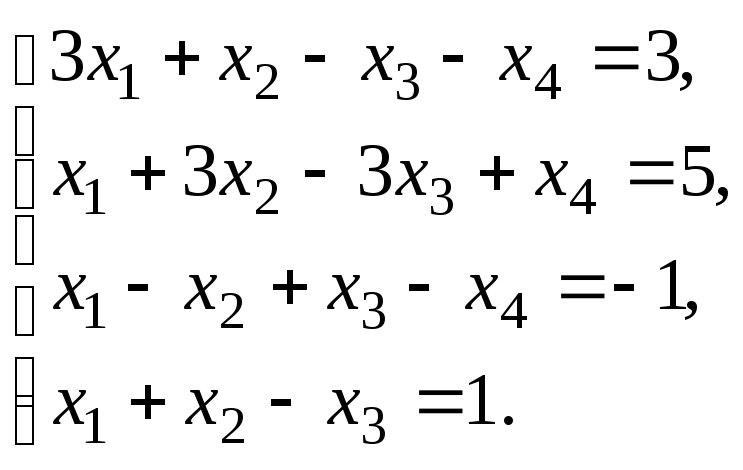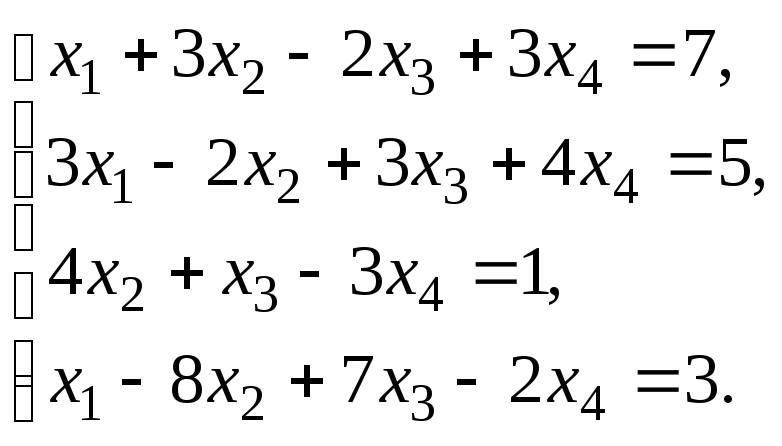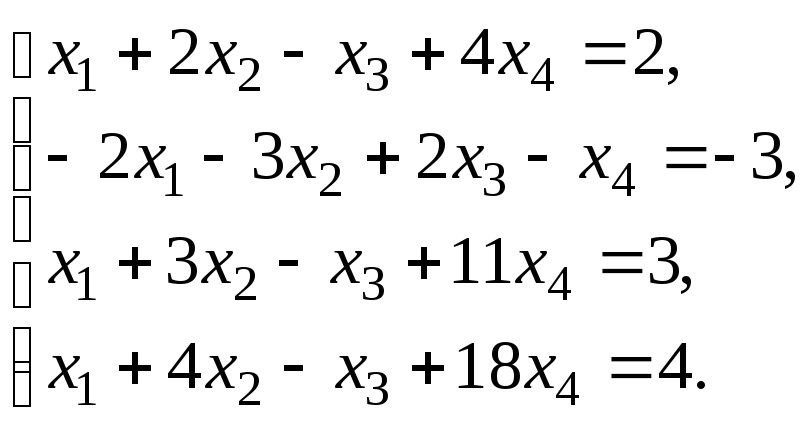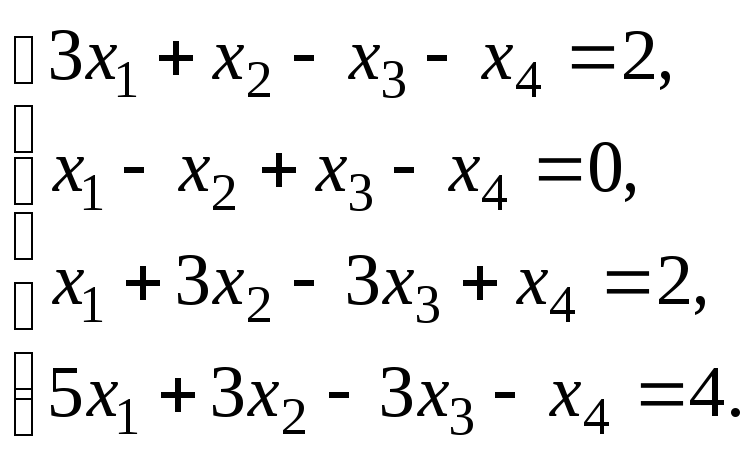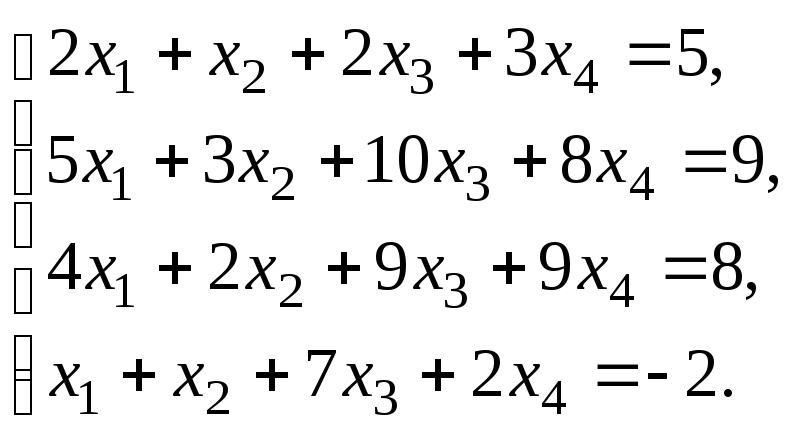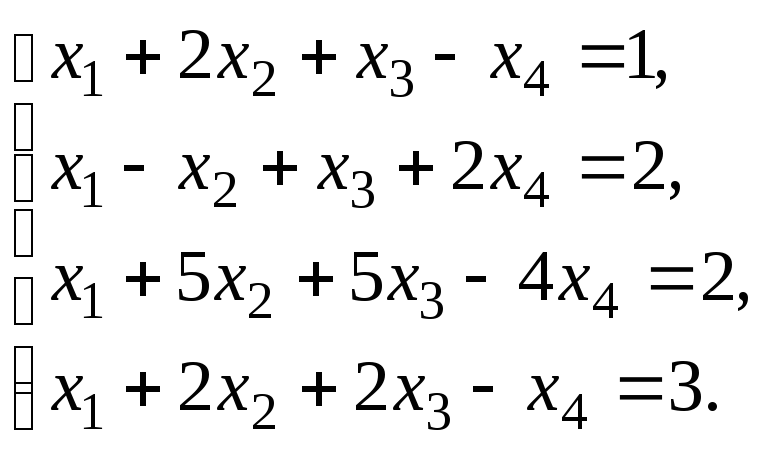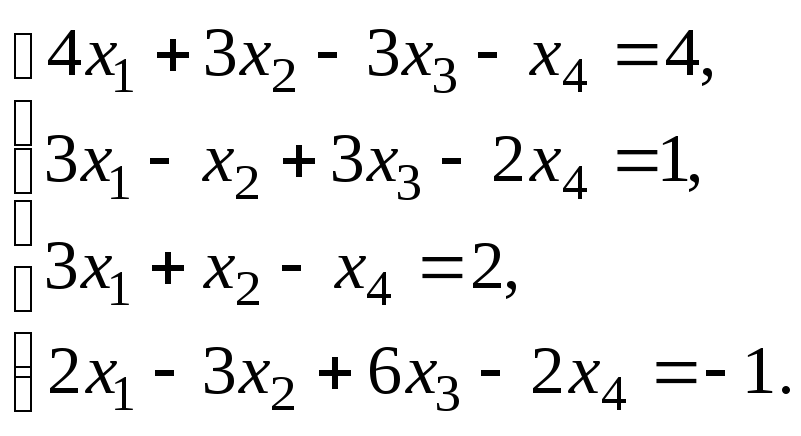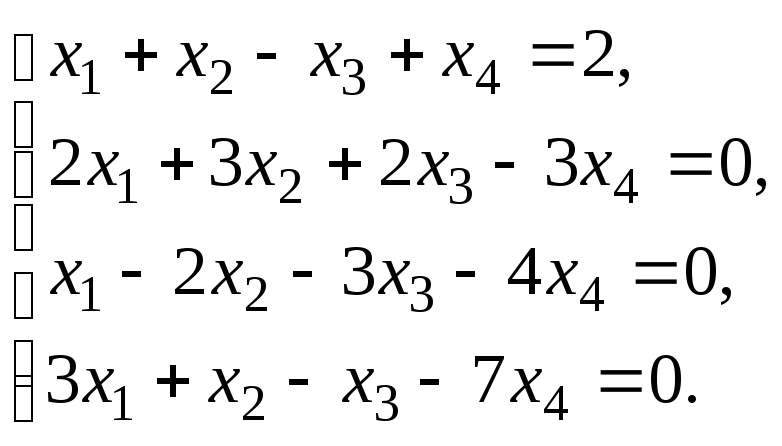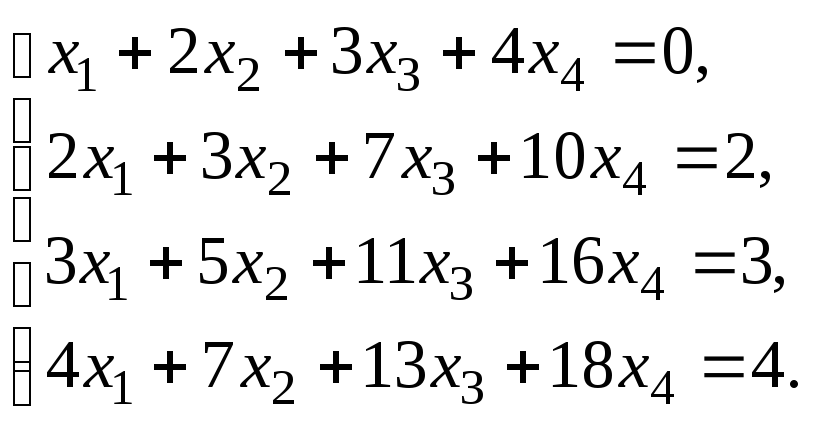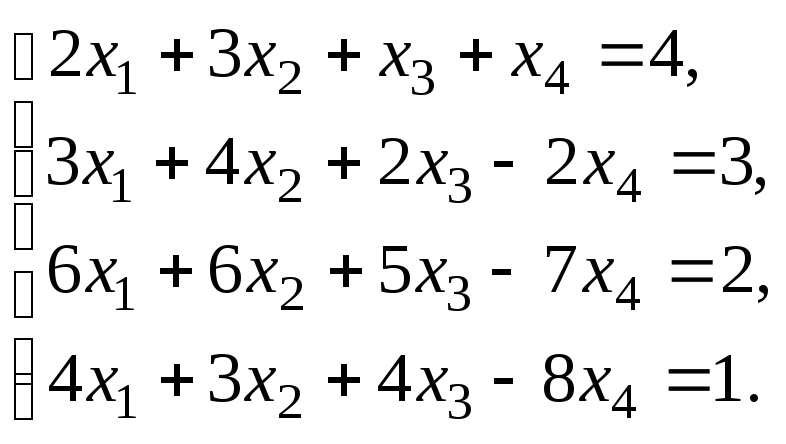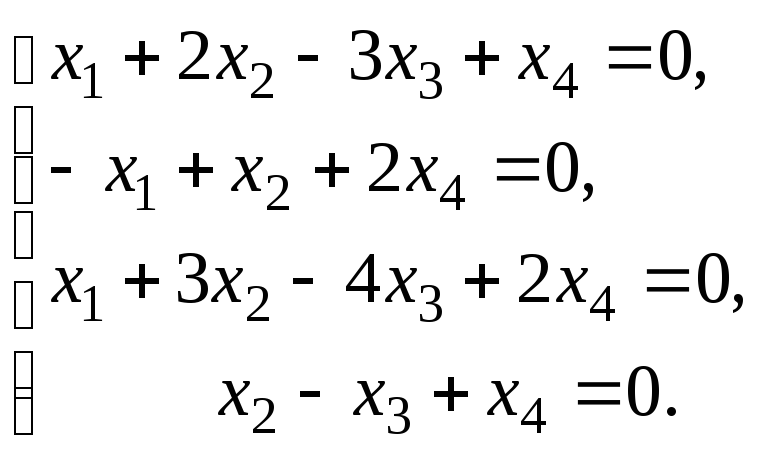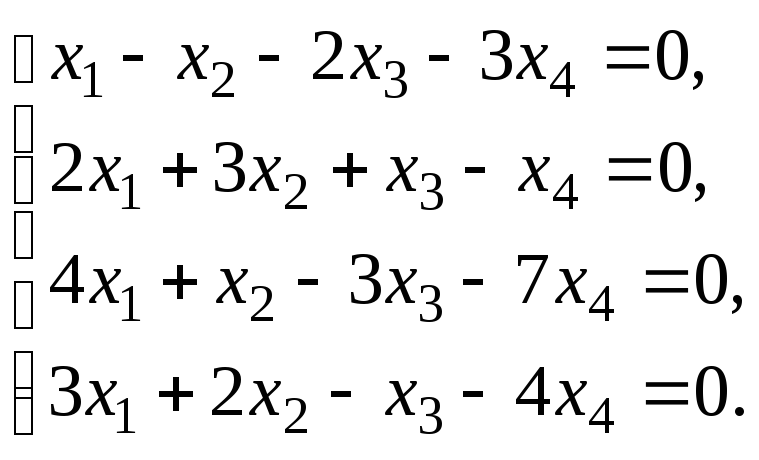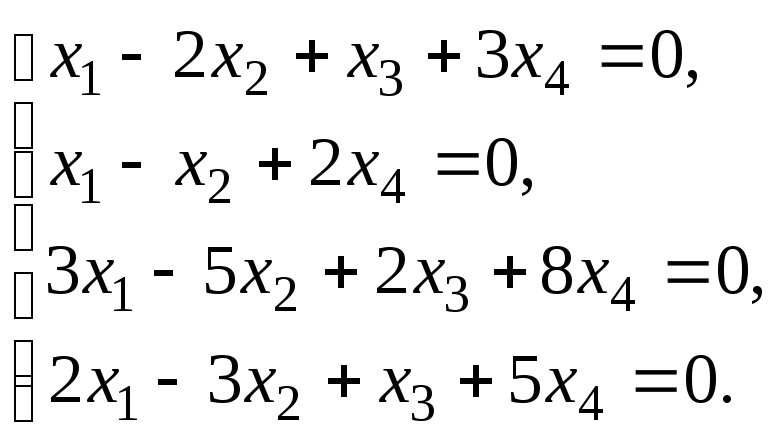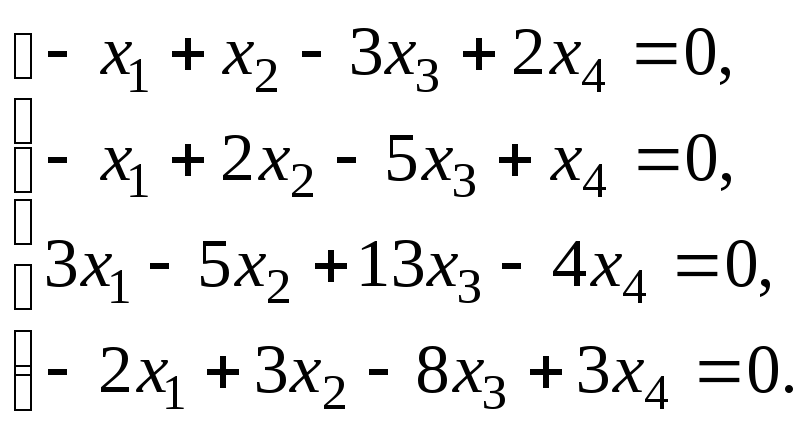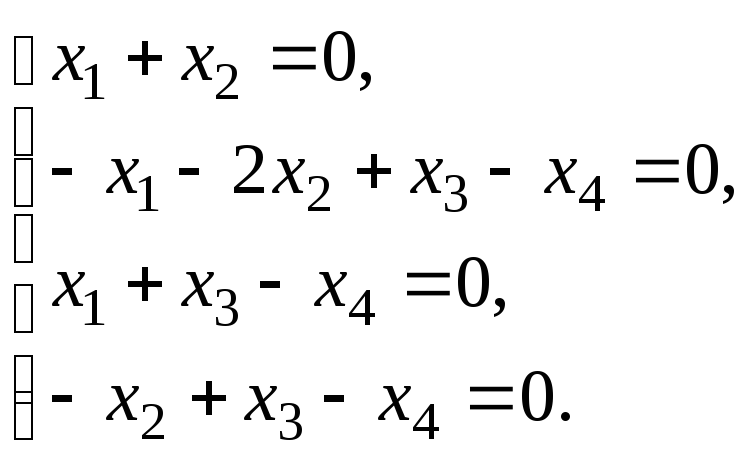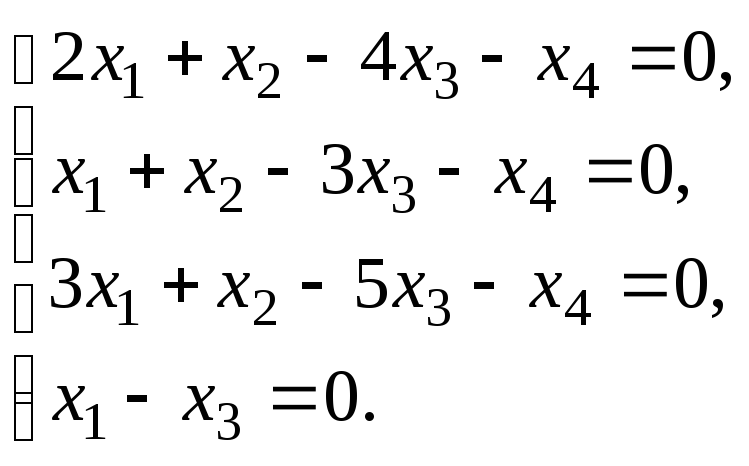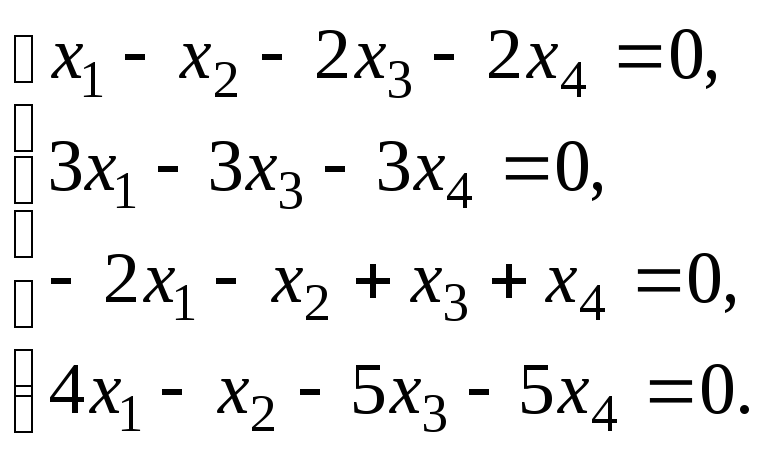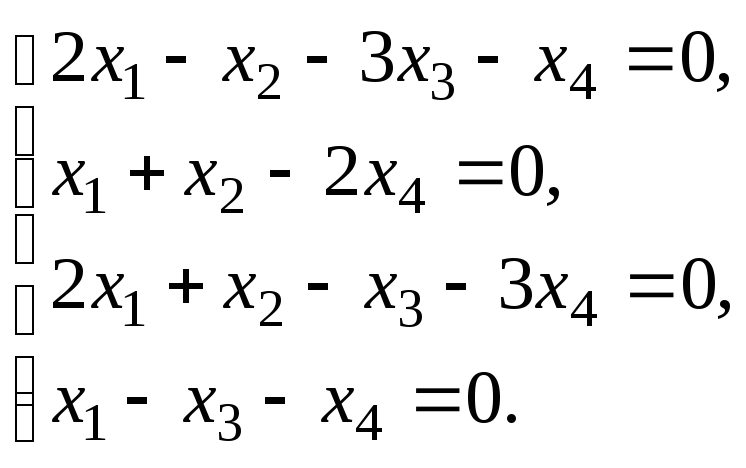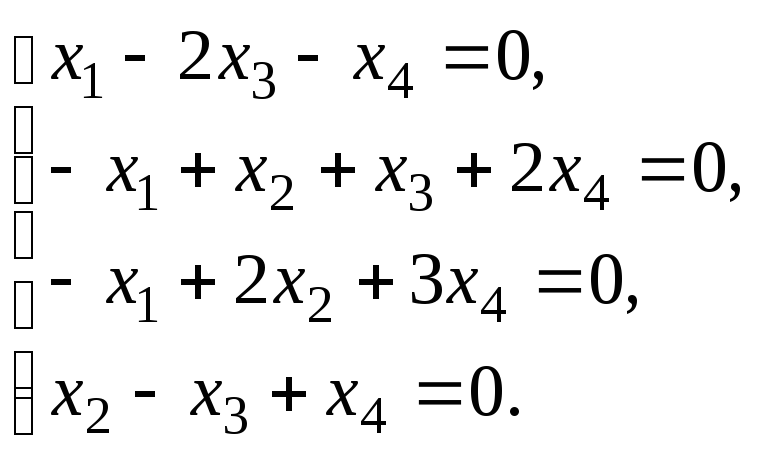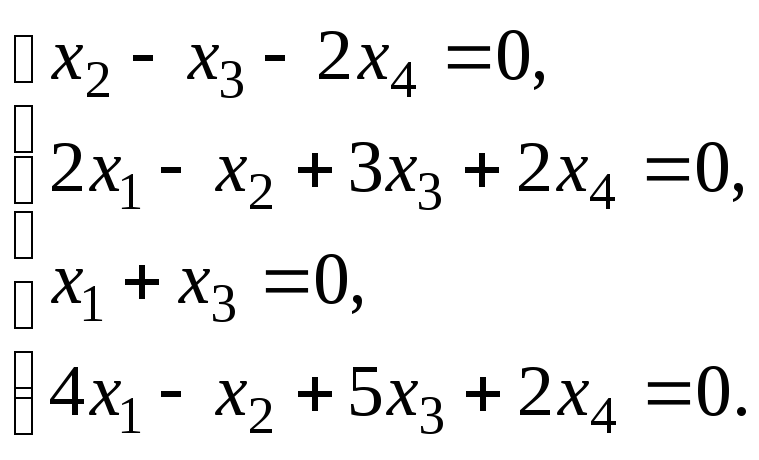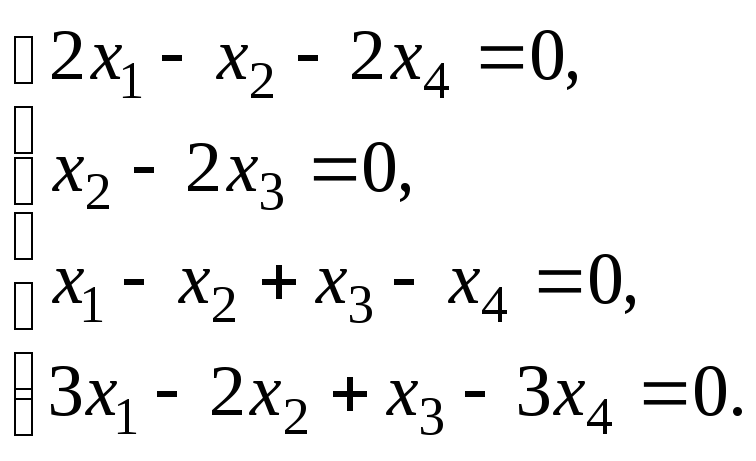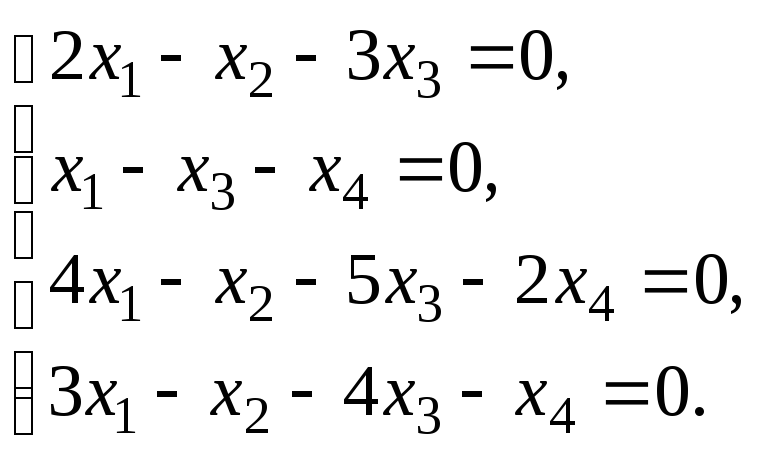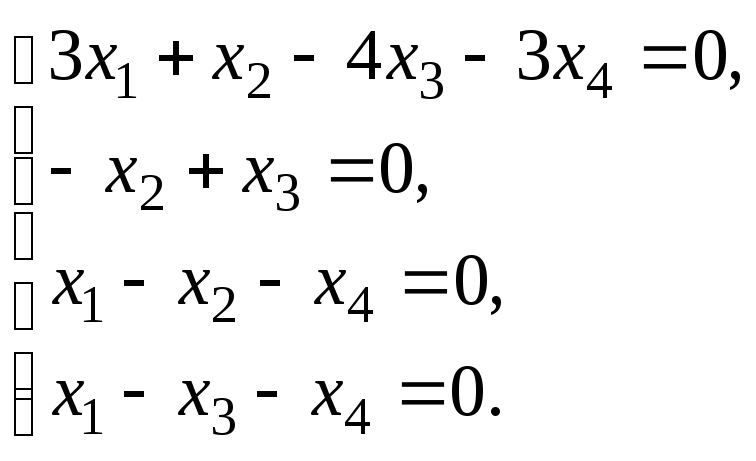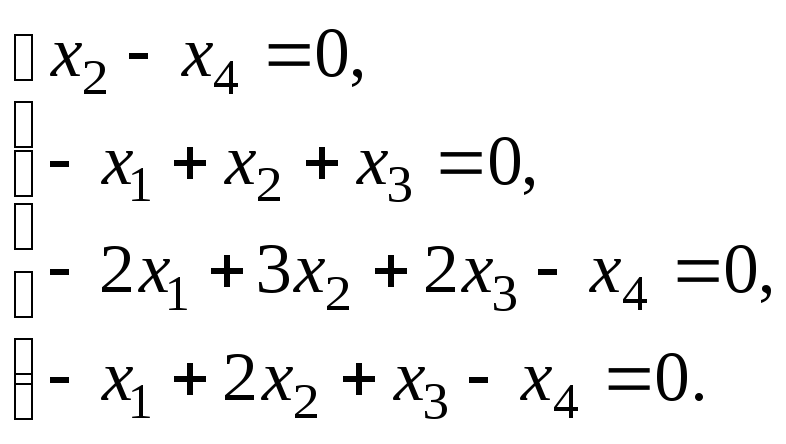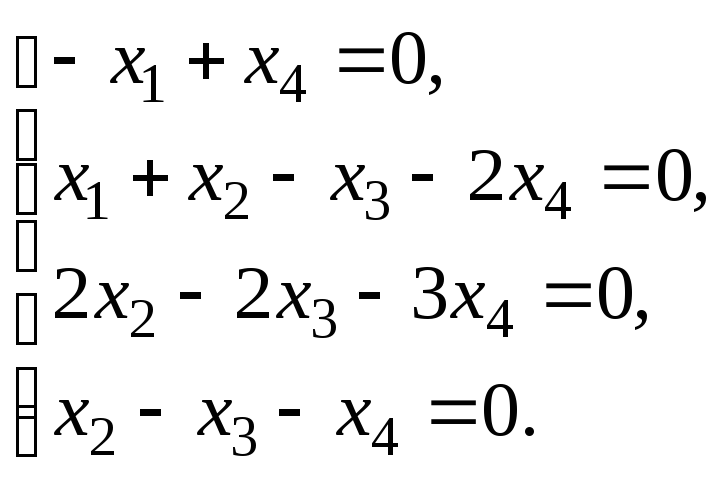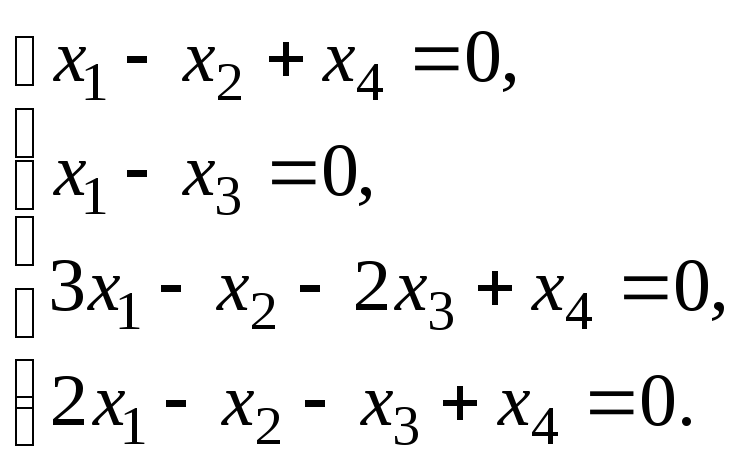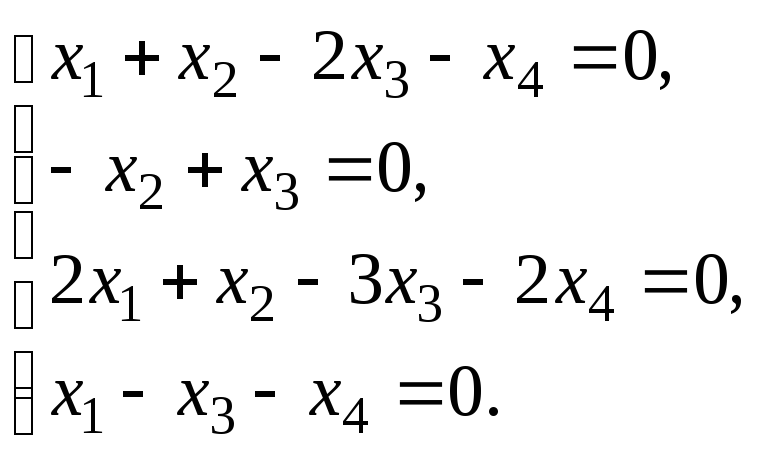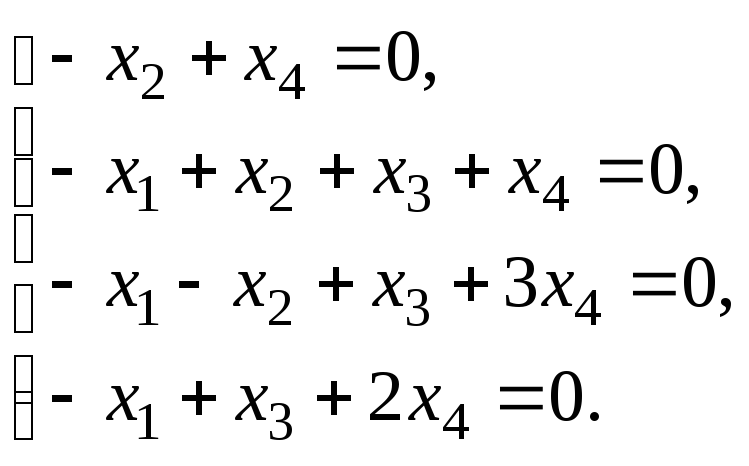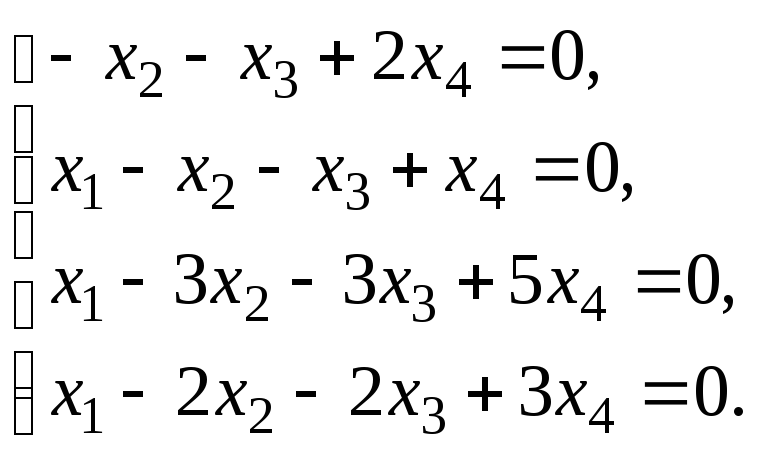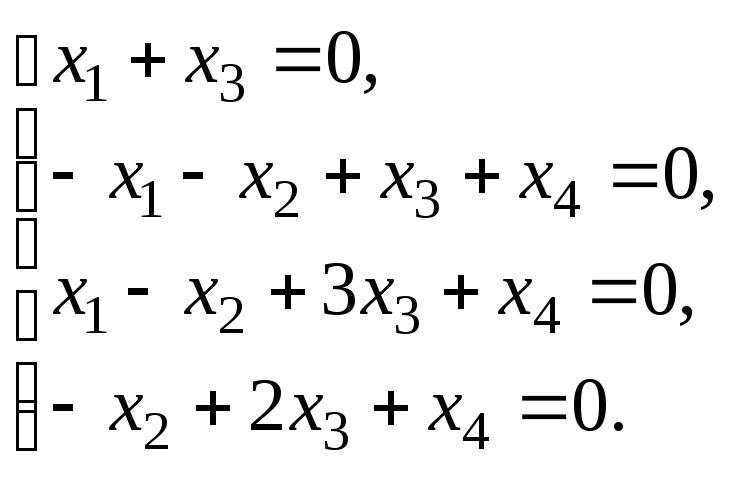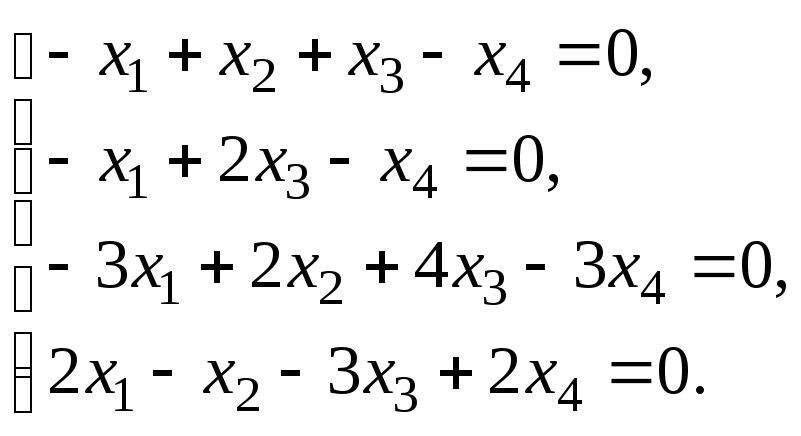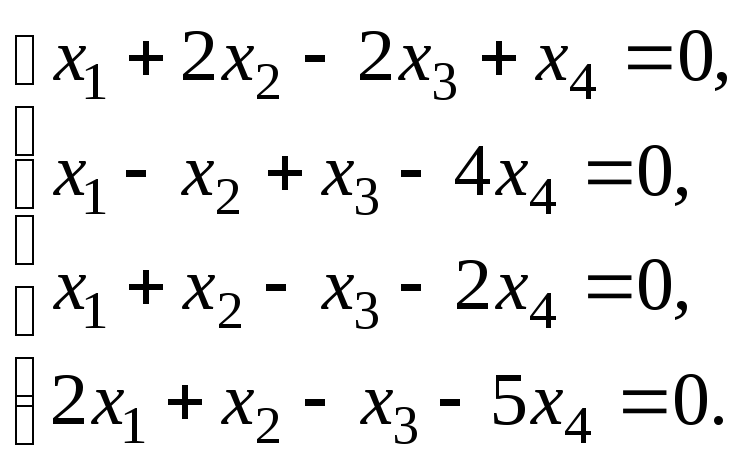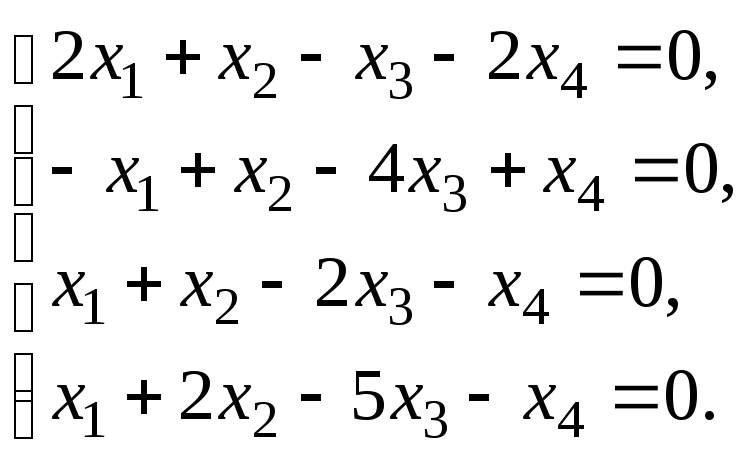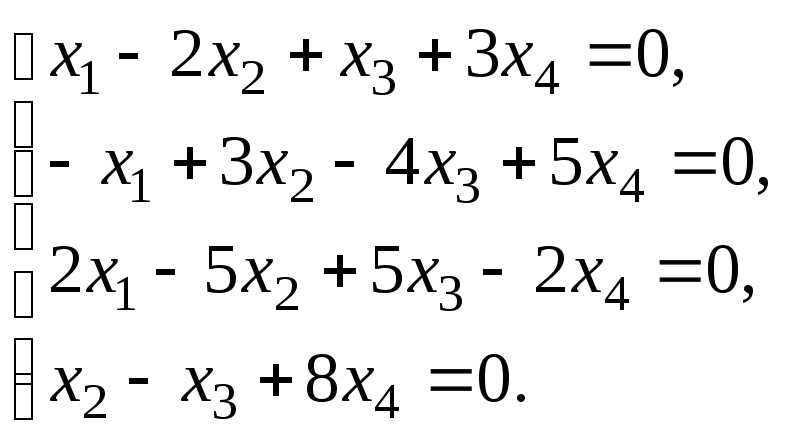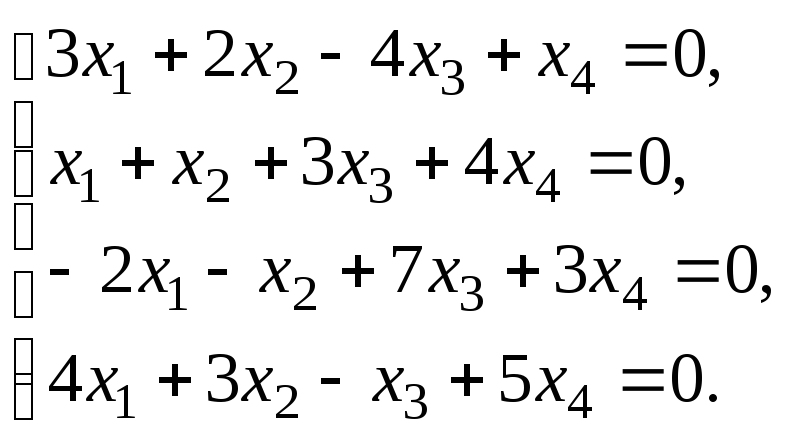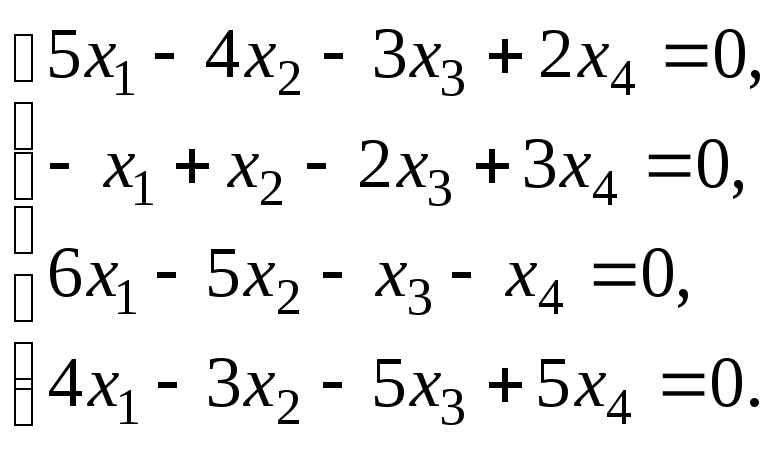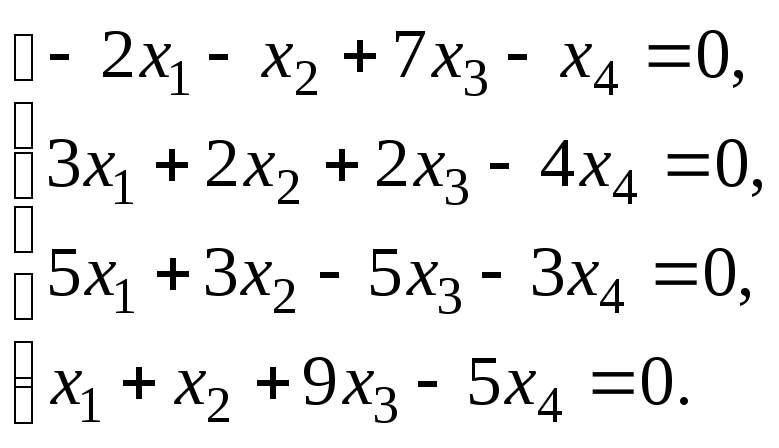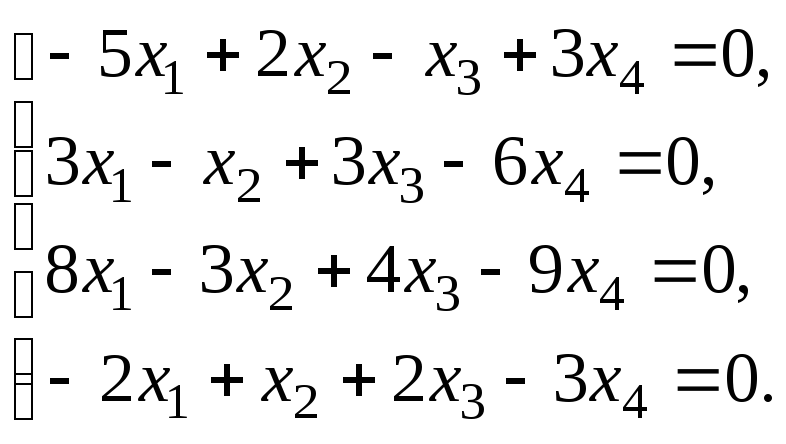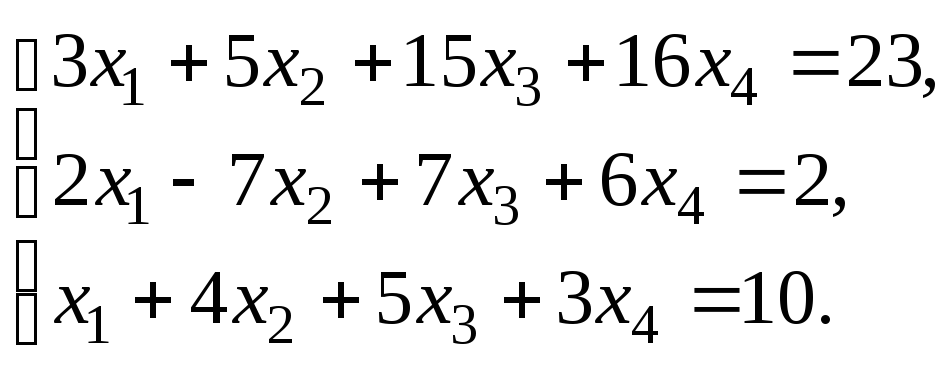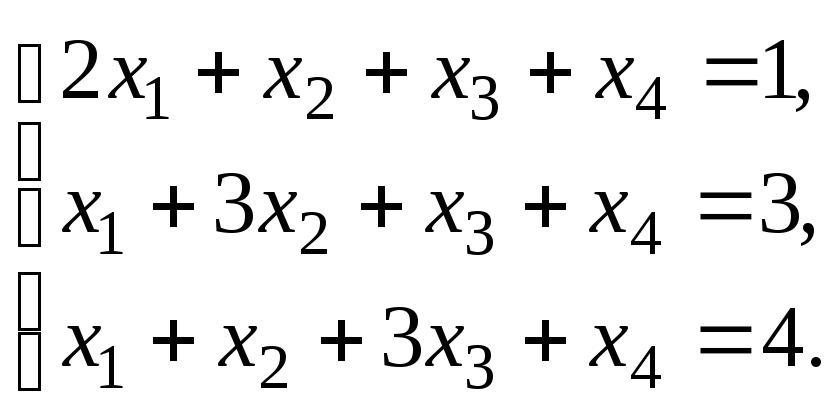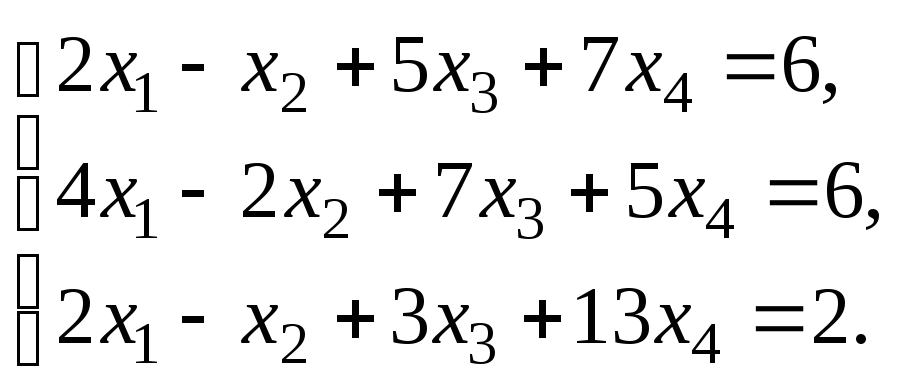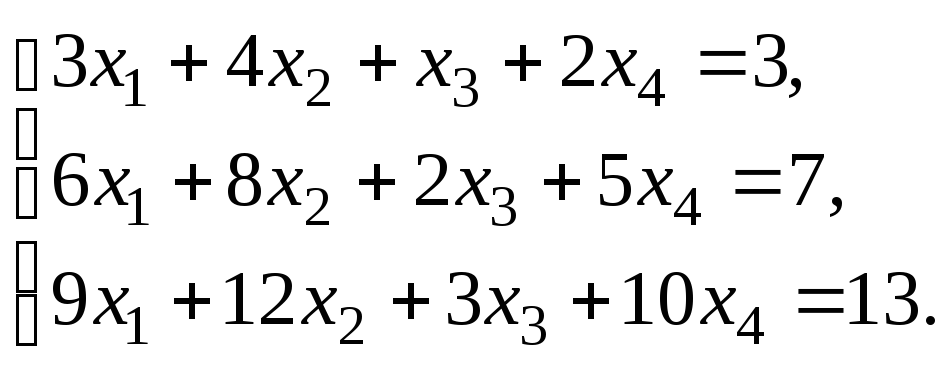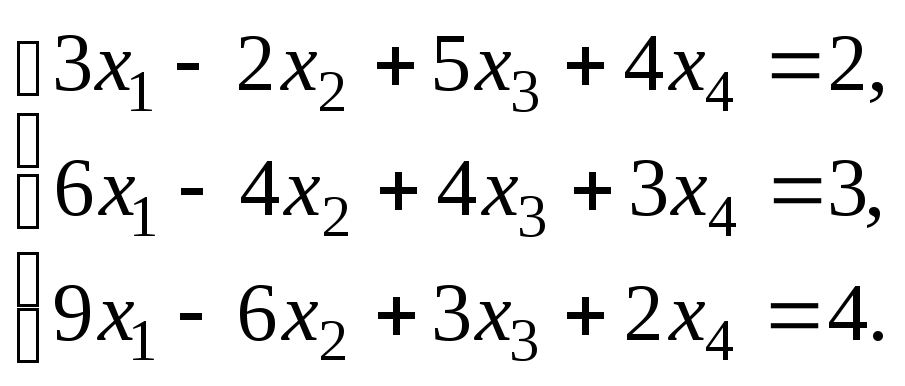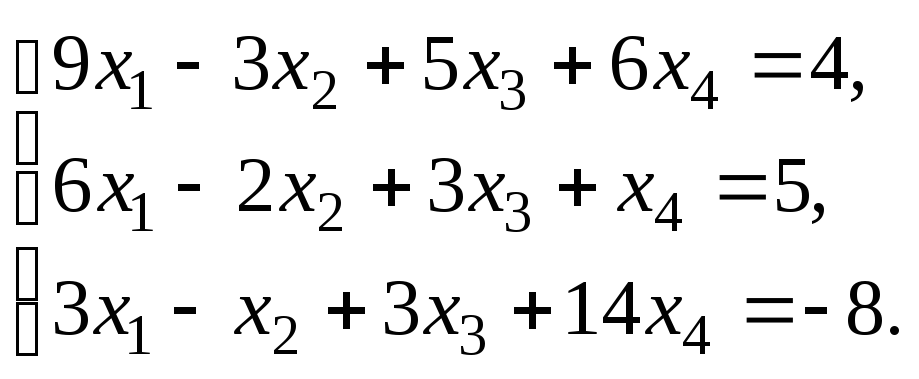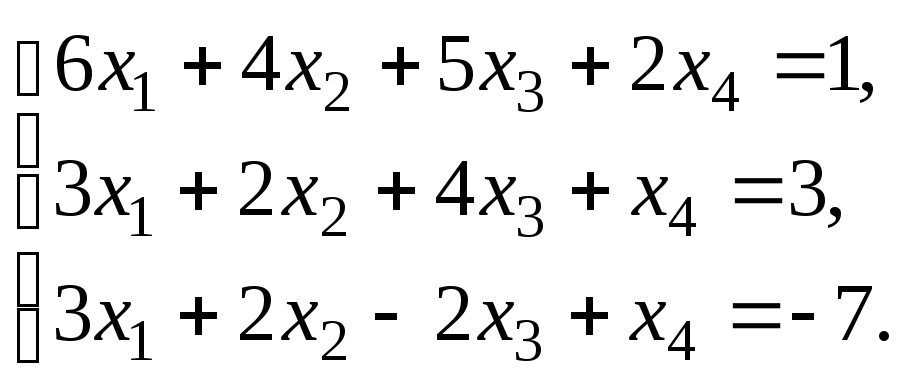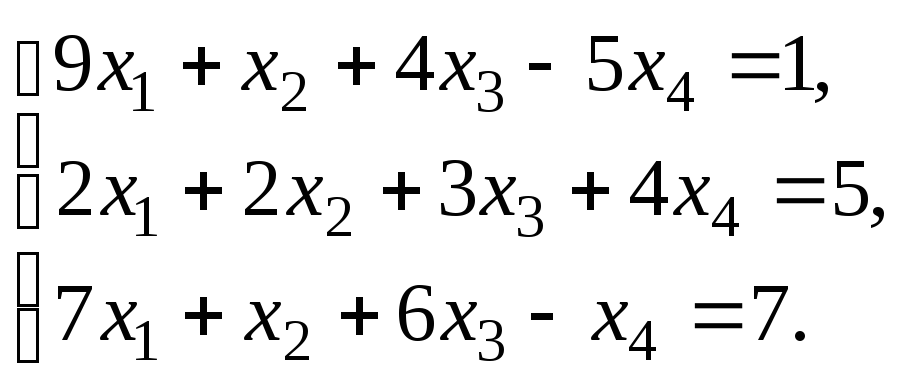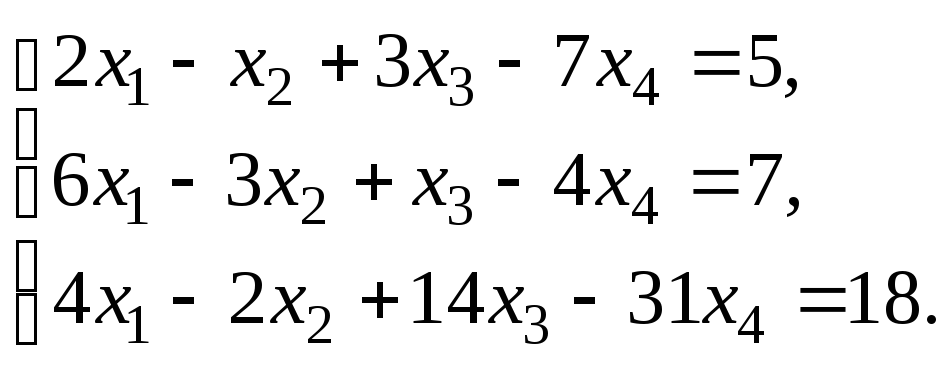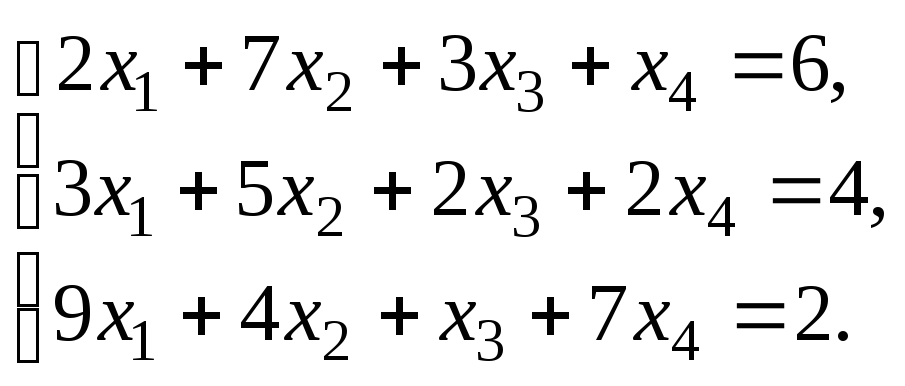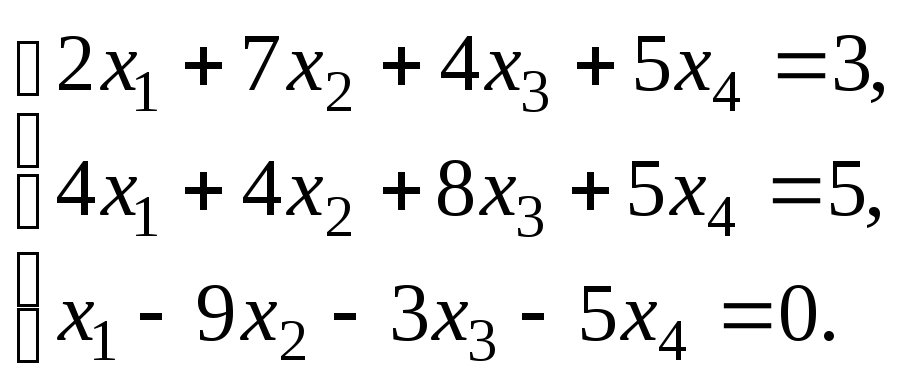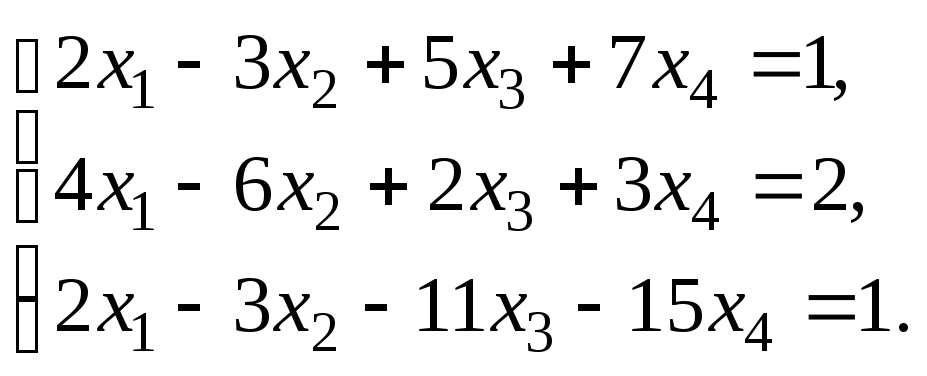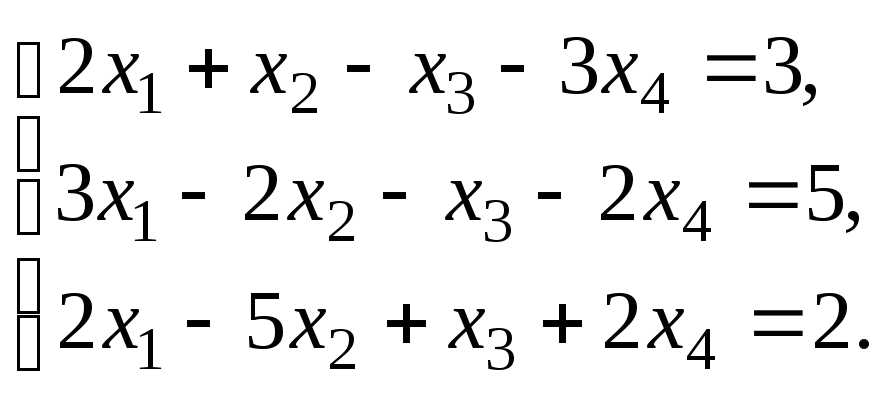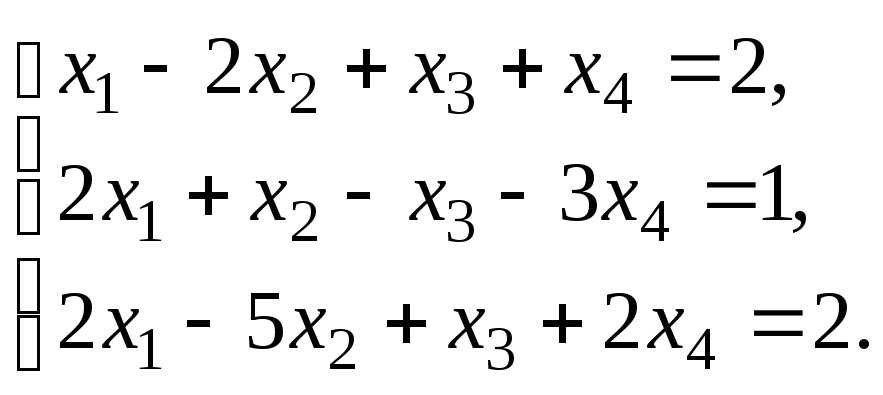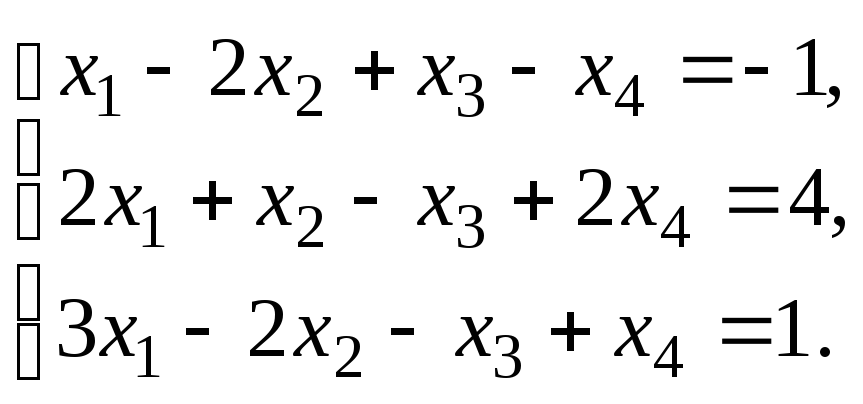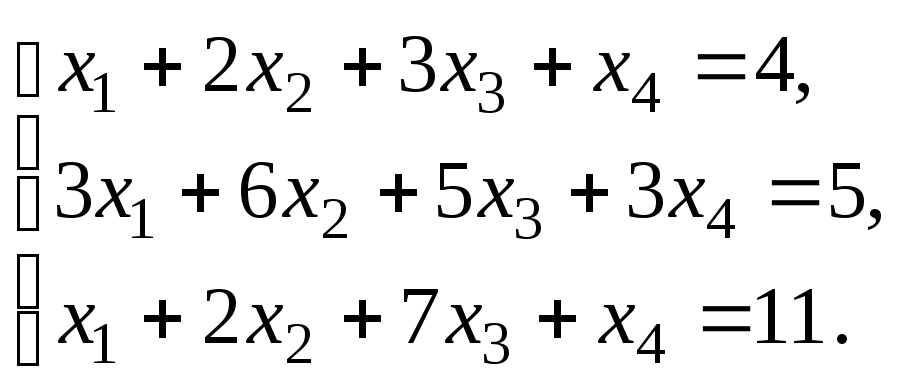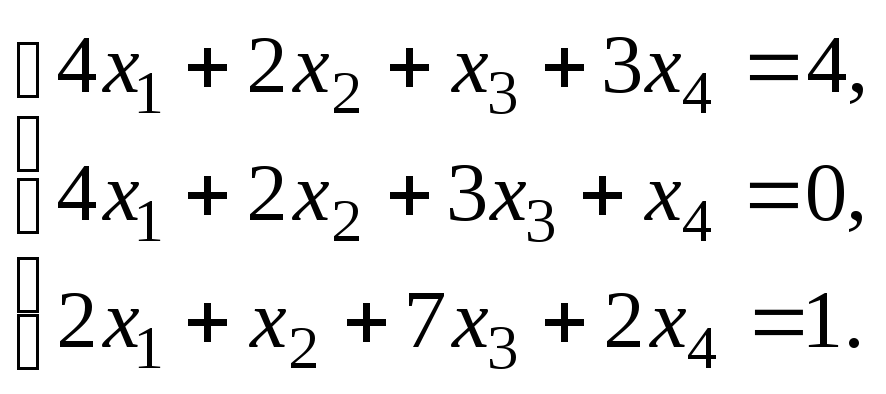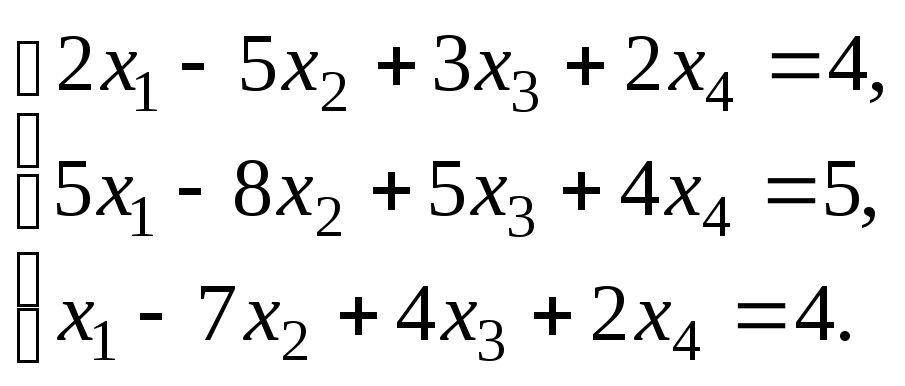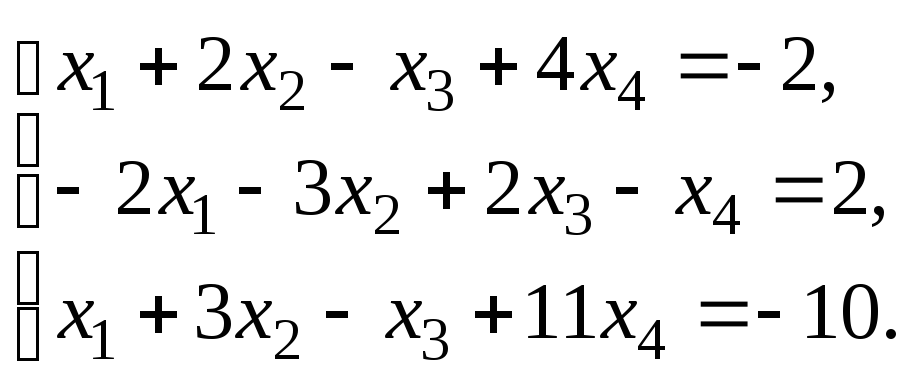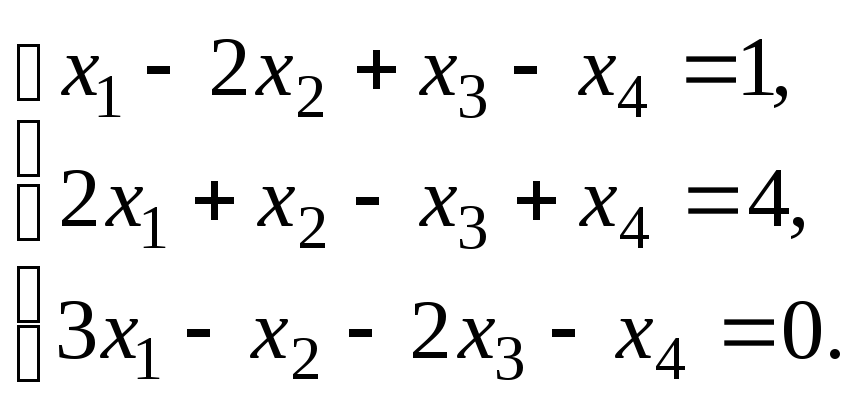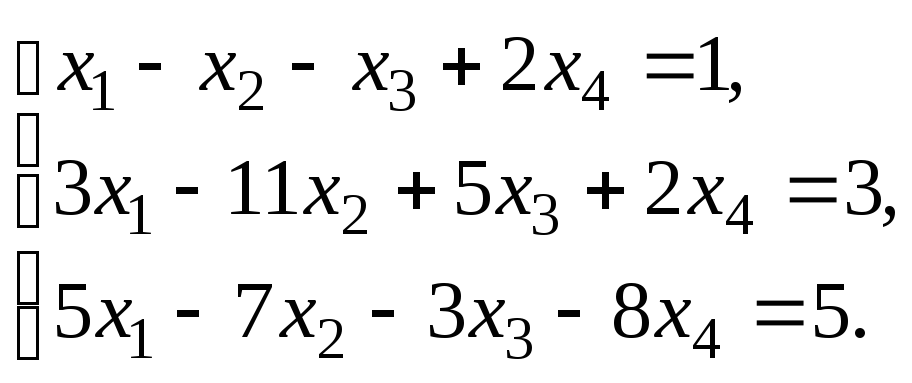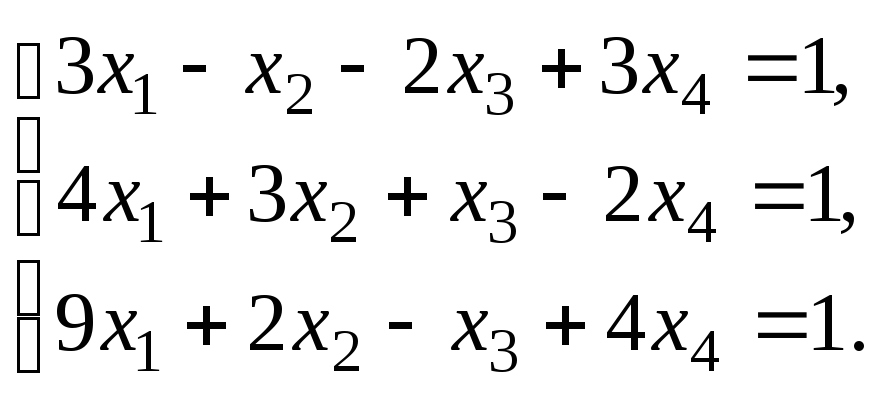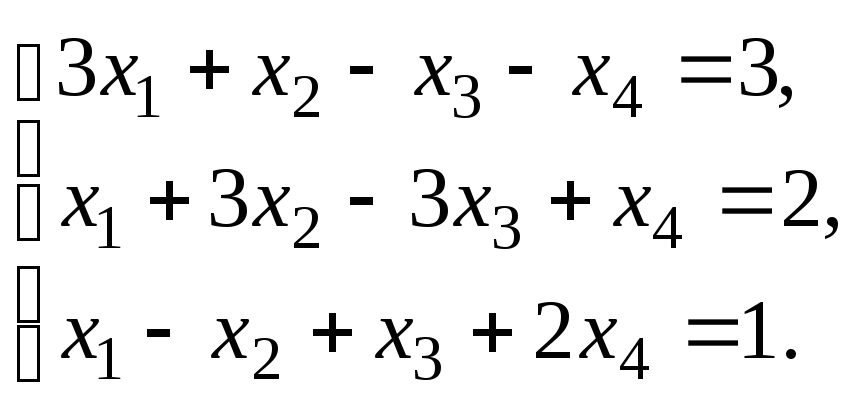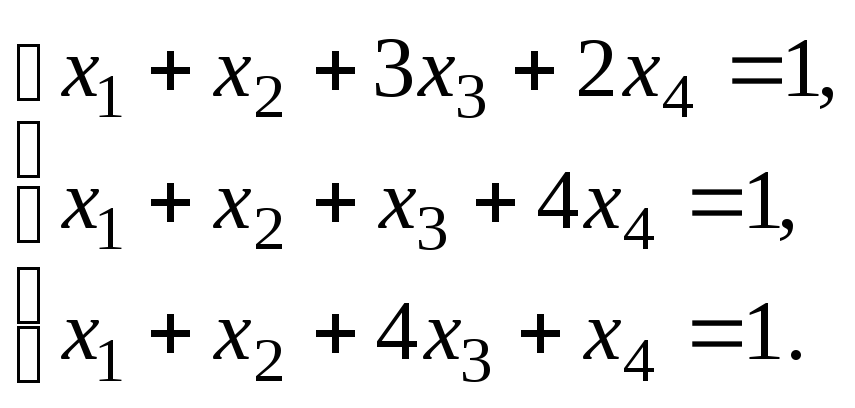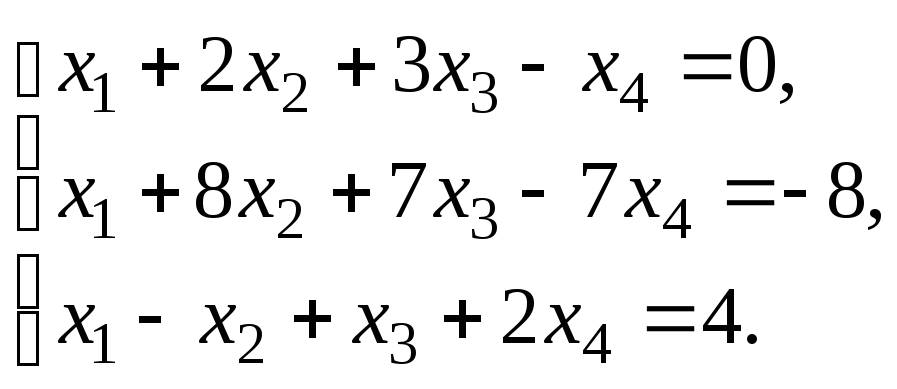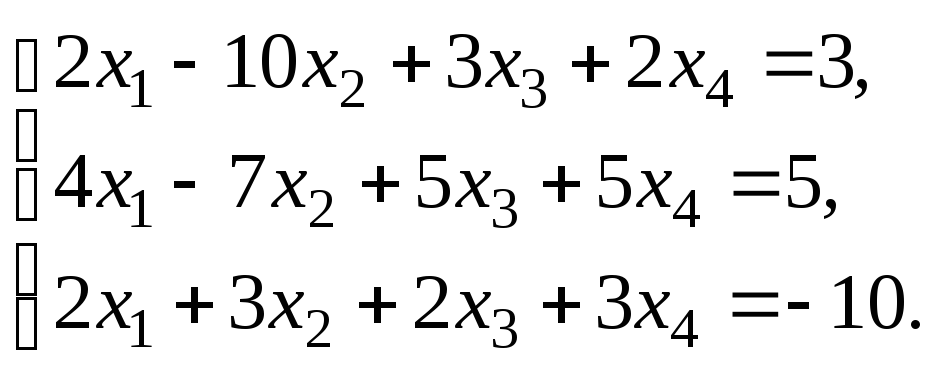§ 6. Системы линейных уравнений.
6.1. Решить систему линейных уравнений по правилу Крамера. Сделать проверку найденного решения.
Общие сведения и расчётные формулы:по представленному заданию.
Решение
системы равнений с использованием
формул Крамера проводится для систем
линейных неоднородных уравнений
![]() -го
порядка в случае, когда уравнений столько
же, сколько и неизвестных:
-го
порядка в случае, когда уравнений столько
же, сколько и неизвестных:
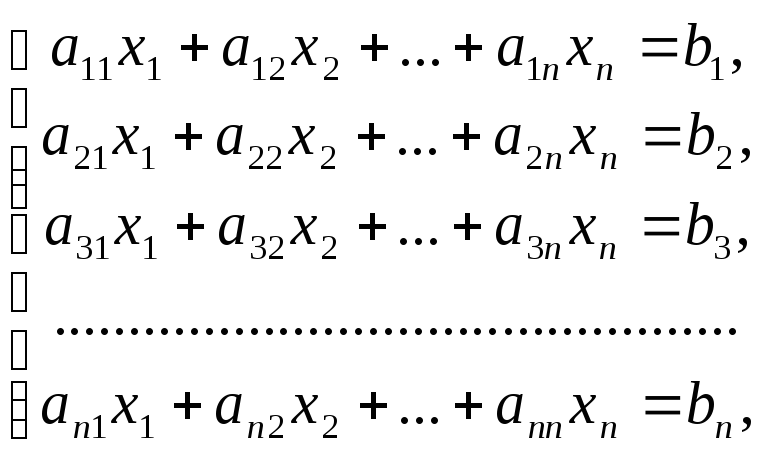 (1)
(1)
где
коэффициенты
![]() ,
,![]() ;
;![]() –
вещественные числа;
–
вещественные числа;
![]() ,
,![]() –
искомые
неизвестные;
–
искомые
неизвестные;
![]() ,
,![]() –
вещественные числа, их называют:
свободные
члены.
Числа:
–
вещественные числа, их называют:
свободные
члены.
Числа:
![]() ,
,
![]() считаем заданными.
считаем заданными.
Системе
уравнений (1) соответствуют: матрица
системы
![]() (составлена из коэффициентов при
неизвестных), матрице соответствует
определитель:
(составлена из коэффициентов при
неизвестных), матрице соответствует
определитель:
![]() =
= ,
,
![]() =
= .
.
Замечание:
решение
системы уравнений с применением формул
Крамера не предполагает построения и
использования расширенной матрицы
![]() .
.
Было
показано, что если
![]() ,
то для записи решений системы уравнений
(3) можно использовать формулы
Крамера:
,
то для записи решений системы уравнений
(3) можно использовать формулы
Крамера:
![]() ,
,
![]() ,
где:
,
где:
![]() =
=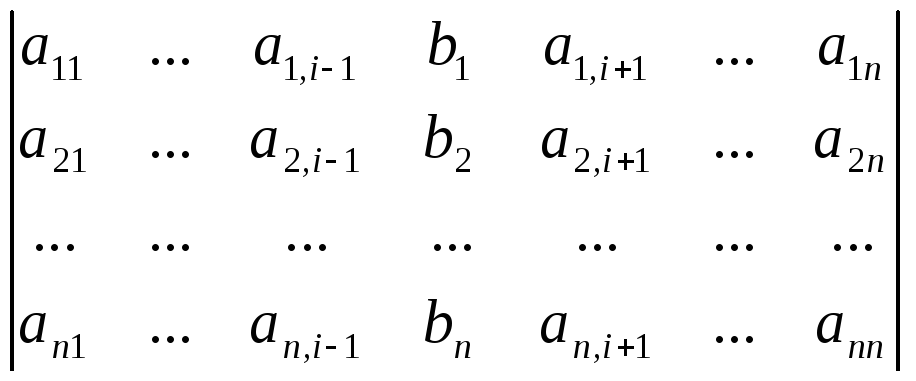 .
.
Формулы
![]() ,
,
![]() ,
определяют единственное
решение, причем не
нулевое,
так как по условию в правой части (3)
имеются не
равные нулю
bi.
,
определяют единственное
решение, причем не
нулевое,
так как по условию в правой части (3)
имеются не
равные нулю
bi.
Трудоемкость применения правила Крамера оценивают трудоемкостью вычисления (n+1)-го определителя n-го порядка. Достоинство метода в том, что в записи решения системы используются только коэффициенты исходного уравнения. Нередко последнее оказывается важным в теоретических исследованиях.
Замечание: при исследовании произвольной системы линейных уравнений (как неоднородных, так и однородных) формулы Крамера так же применяют, но только после того, как проведено общее исследование системы методом Гаусса или применением теоремы Кронекера-Капелли.
Ниже рассмотрены примеры решения систем уравнений с использованием формул Крамера.
Примеры (и образец оформления):
Пример
–1:
Решить систему уравнений:
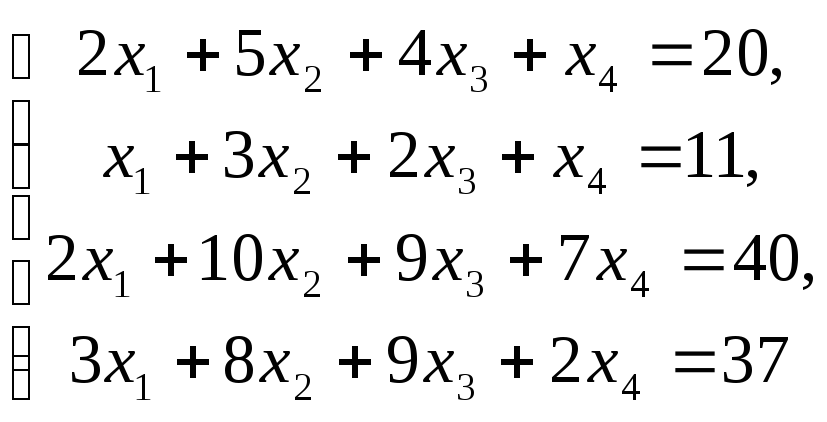 по правилу Крамера.
по правилу Крамера.
Решение:
1)
Используя коэффициенты левой части
заданной системы линейных уравнений,
запишем определитель: ![]() =
=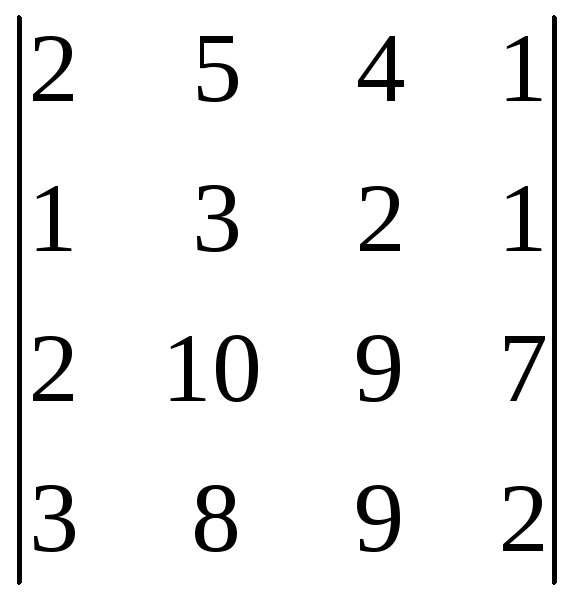 и вычислим его:
и вычислим его:
![]() =–3.
=–3.
2) Вычислим определители:
![]() =
=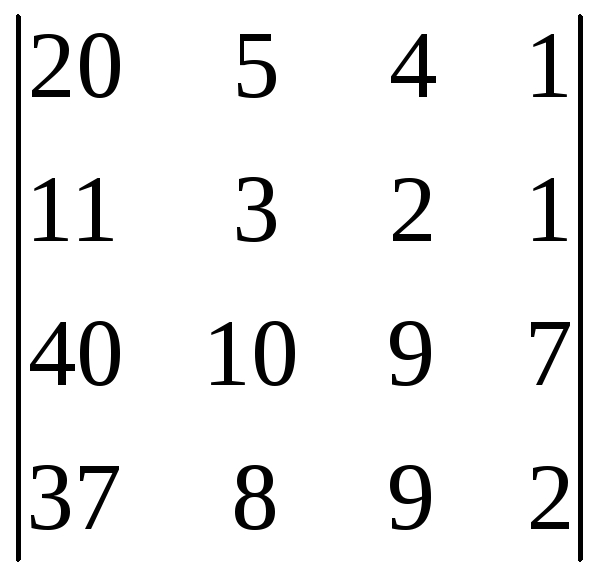 =–3,
=–3,
![]() =
=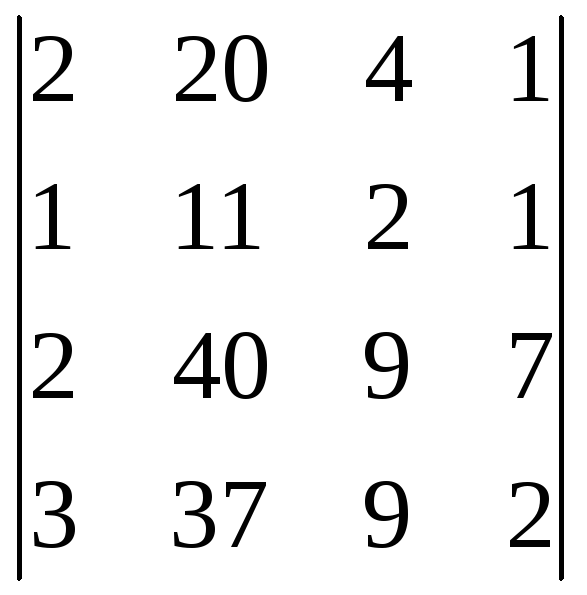 =–6,
=–6,
![]() =
=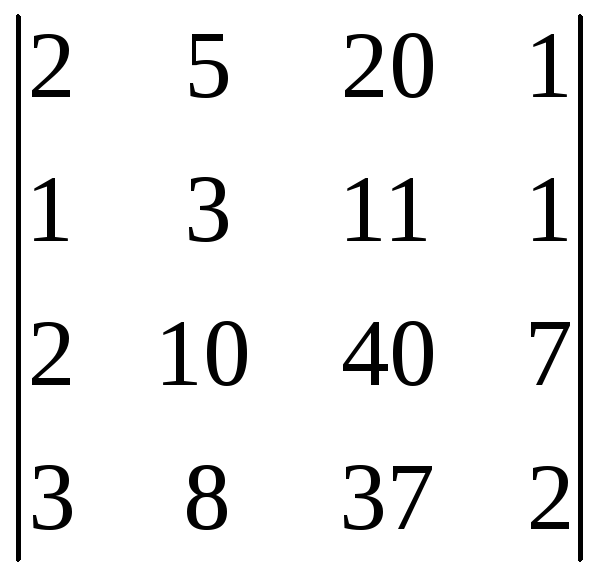 =–6,
=–6,
![]() =
=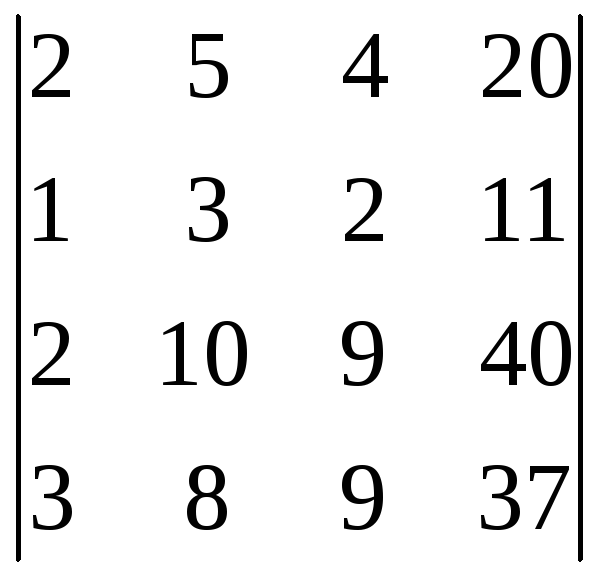 =0.
=0.
2)
Применяя формулы Крамера:
![]() ,
,
![]() ,
получаем:
,
получаем:
![]() =1,
=1,
![]() =
=![]() =2,
=2,
![]() =0.
=0.
Ответ: решение: (1,2,2,0).
Пример
–2:
Решить систему уравнений:
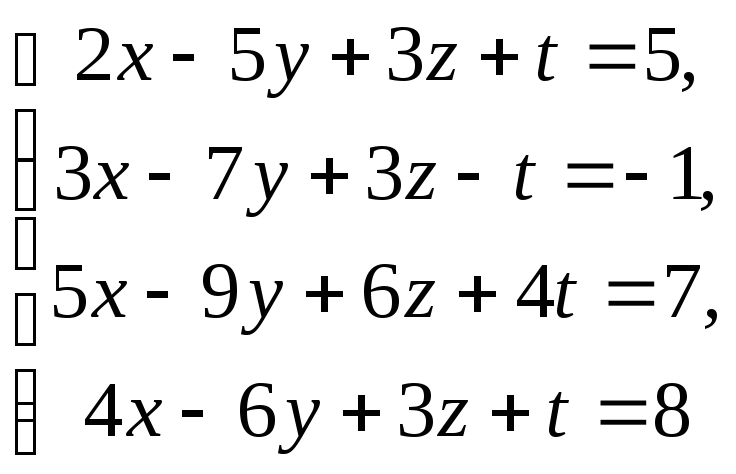 по правилу Крамера.
по правилу Крамера.
Решение:
1)
Используя коэффициенты левой части
заданной системы линейных уравнений,
запишем определитель: ![]() =
= и вычислим его:
и вычислим его:
![]() =0.
=0.
Замечание:
так как
![]() =0,
то задание решить
систему уравнений с применением формул
Крамера не выполнима, и автор решения
вправе заявить об этом и далее не
исследовать систему; только
любопытство может подвигнуть нас на
продолжение!
=0,
то задание решить
систему уравнений с применением формул
Крамера не выполнима, и автор решения
вправе заявить об этом и далее не
исследовать систему; только
любопытство может подвигнуть нас на
продолжение!
2) Вычислим определители:
![]() =
=
![]() 0
→ видим:
0
→ видим:
![]() невозможно. Вычислять
невозможно. Вычислять
![]() ,
,![]() ,
,![]() нет смысла!
нет смысла!
Ответ: решений нет.
Варианты индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
Вар. |
Задание: |
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|
6.2. Решить систему линейных уравнений методом Гаусса. Сделать проверку найденного решения.
Общие сведения и расчётные формулы:по представленному заданию.
Метод Гаусса называют часто методом последовательного исключения неизвестных. Для реализации этого метода удобно оперировать не с исходной записью системы в виде (1), а с матрицей коэффициентов системы:
 , (1)
, (1)
её принято называть расширенной матрицей системы уравнений.
Метод
Гаусса заключается в последовательном
применении к строкам
матрицы
![]() эквивалентных
преобразований, приводящих эту матрицу
к трапецоидальному
или треугольному
(в частном случае) виду. В результате
реализации метода получим:
эквивалентных
преобразований, приводящих эту матрицу
к трапецоидальному
или треугольному
(в частном случае) виду. В результате
реализации метода получим:
▫ система уравнений будет несовместной, если в процессе преобразований получается уравнение, в котором коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля; если же такое уравнение не встретим, то система будет совместной;
▫ если система совместной, то она будет определенной, если она приводится к треугольному виду, и неопределенной, если приводится к трапецоидальному виду.
В основном метод применяют в тех случаях, когда не предполагается исследование технической системы: нужна лишь оценка (подтверждение) реакции системы на конкретные внешние воздействия.
Трудоемкость
метода Гаусса оценивают трудоемкостью
вычисления одного определителя
![]() -го
порядка.
-го
порядка.
Рассмотренные ниже примеры решения систем уравнений с использованием метода Гаусса достаточно полно иллюстрируют его возможности.
Примеры (и образец оформления):
Пример
–1:Решить систему
линейных уравнений:
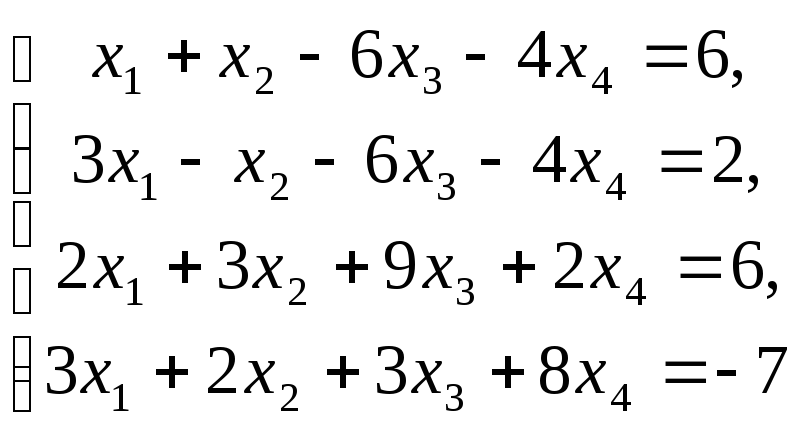 методом Гаусса.
методом Гаусса.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
1
1
-6
-4
6
1
2
-3
0
3
3
-1
-6
-4
2
0
-7
3
-4
-7
2
3
9
2
6
=(1)→
0
-1
15
2
0
=(2)→
3
2
3
8
-7
0
1
3
4
-3
-
1
2
-3
0
3
1
2
-3
0
3
0
-3
3
0
-5
0
0
0
8
-12
0
-1
15
2
0
=(3)→
0
-1
15
2
0
=(4)→
0
0
6
2
-1
0
0
6
2
-1
Выполнены операции: (1): [R4]–[R2]; [R4] делим на 3; [R1]–[R4]; [R2]–[R1]·3; [R3]–[R1]·2. (2): [R2]+[R4]; [R2] делим на 2; [R4]+[R3]; [R4] делим на 3. (3): [R2]–[R3]·3; [R2]+[R3]·7. (4): получение результата.
2). Получены результаты: - система совместна;
- ранг системы равен 4 → решение системы единственно.
3). Из уравнения
[R2] следует:![]() =
=![]() ;
далее из уравнения [R2]:
6
;
далее из уравнения [R2]:
6![]() =
=![]() ,
откуда вычисляем:x3=
,
откуда вычисляем:x3=
![]() ;из уравнения
[R3]:
;из уравнения
[R3]:
![]() =
=![]() ,
откуда вычисляем:
,
откуда вычисляем:![]() =
2; из
уравнения [R1]:
=
2; из
уравнения [R1]:
![]() =
=![]() ,
откуда вычисляем:
,
откуда вычисляем:![]() =0.
=0.
Ответ: (0,
2,
![]() ,
–
,
–![]() ).
).
Пример–2:Решить систему
линейных уравнений:
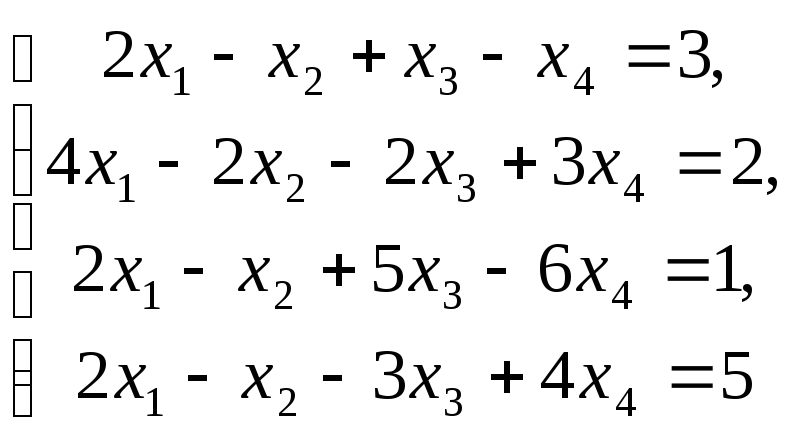 методом Гаусса.
методом Гаусса.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
2
-1
1
-1
3
2
-1
1
-1
3
4
-2
-2
3
2
0
0
-4
-5
-4
2
-1
5
-6
1
=(1)→
0
0
4
-5
-2
=(2)→
2
-1
-3
4
5
0
0
-4
5
2
|
2 |
-1 |
1 |
-1 |
3 |
|
|
|
0 |
0 |
-4 |
-5 |
-4 |
|
|
|
0 |
0 |
0 |
0 |
2 |
=(3)→ | |
|
0 |
0 |
0 |
0 |
0 |
|
|
Выполнены операции: (1): [R4]–[R1]; [R3]–[R1]; [R2]–[R1]·2. (2): [R4]+[R3]; [R3]–[R2]. (3): видим: [R3] – невозможна.
2). Получены результаты: - система несовместна.
Ответ: система несовместна.
Пример–3:Решить систему
линейных уравнений:
 методом Гаусса.
методом Гаусса.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
9
-3
5
6
4
3
-1
2
2
-1
6
-2
3
4
5
=(1)→
3
-1
0
-10
13
=(2)→
3
-1
3
14
-8
0
0
1
12
-7
-
3
-1
2
2
-1
3
-1
2
2
-1
0
0
-1
-6
7
=(3)→
0
0
-1
0
7
=(4)→
0
0
0
6
0
0
0
0
6
0
Выполнены операции: (1): [R1]–[R2]; [R2]–[R3]; [R3]–[R1]. (2): [R2]–[R1]; делим строку [R2] на 2; [R3]+[R2]. (3): [R2]+[R3]; [R4]+[R2]. (4): раскрываем таблицу и вычисляем все неизвестные.
2). Получены результаты: - система совместна;
- ранг системы
равен 3 → свободная неизвестная
![]() =
=![]() .
.
3). Из уравнения
[R3] следует:![]() =0;
далее из уравнения [R2]:
=0;
далее из уравнения [R2]:
![]() =–7;
раскрывая уравнение
[R1], получаем:
=–7;
раскрывая уравнение
[R1], получаем:
![]() =
=![]() =
=![]() .
.
4). Получили общее решение заданной системы, записываем ответ.
Ответ:
![]() .
.
Замечание: любая промежуточная ошибка в цепочке вычислений может быть исправлена от места обнаруженной ошибки.
Варианты индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
Вар. |
Задание: |
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|
6.3. Найти общее решение и ФСР системы линейных однородных уравнений. Сделать проверку найденного решения.
Общие сведения и расчётные формулы:по представленному заданию.
Общая схема решения произвольной системы линейных однородных уравнений:
A1*:
Вычисляем ранг
![]() матрицы
матрицы
![]() коэффициентов системы уравнений.
Так
как для однородной системы уравнений
коэффициентов системы уравнений.
Так
как для однородной системы уравнений
![]() =
=![]() ,
то всегда выполняется
,
то всегда выполняется
![]()
![]()
![]() .
Однородная система уравнений всегда
совместна. Пусть
.
Однородная система уравнений всегда
совместна. Пусть
![]() =
=![]() .
Это значит, что определён базовый
минор
M
.
Это значит, что определён базовый
минор
M![]() матрицы
матрицы
![]() системы уравнений.
системы уравнений.
A2*:
В системе уравнений оставляем только
те
![]() уравнения-строки, которые попали
в базовый минор:
остальные являются следствием выделенных.
уравнения-строки, которые попали
в базовый минор:
остальные являются следствием выделенных.
A3*:
В левой части каждого из оставшихся для
дальнейшего решения уравнений оставляем
те
![]() столбцов с неизвестными, которые попали
в базовый минор:
остальные неизвестные объявляем
свободными
и соответствующие столбцы с ними
переносим в правую часть. Учтём, что
свободных неизвестных
столбцов с неизвестными, которые попали
в базовый минор:
остальные неизвестные объявляем
свободными
и соответствующие столбцы с ними
переносим в правую часть. Учтём, что
свободных неизвестных
![]() .
.
A4*: Находим решения преобразованной системы уравнений, применяя формулы Крамера: определитель преобразованной системы не равен нулю!
A5*: Полученное решение системы называют общим: вычисленные по формулам Крамера неизвестные выражаются через свободные неизвестные. Присваивая свободным неизвестным произвольные значения, получаем частные решения.
A6*:
Выбирая
![]() независимых частных решений, определяем
вычисляемые
независимых частных решений, определяем
вычисляемые
![]() неизвестных. Полученные таким образом
векторы-решения могут быть приняты в
качестве ФСР.
неизвестных. Полученные таким образом
векторы-решения могут быть приняты в
качестве ФСР.
Замечание: выбор свободных неизвестных определяет тот, кто исследует заданную систему уравнений, используя или метод Гаусса, или теорему Кронекера-Капелли.
Примеры (и образец оформления):
Пример
–1:
Исследовать систему уравнений:
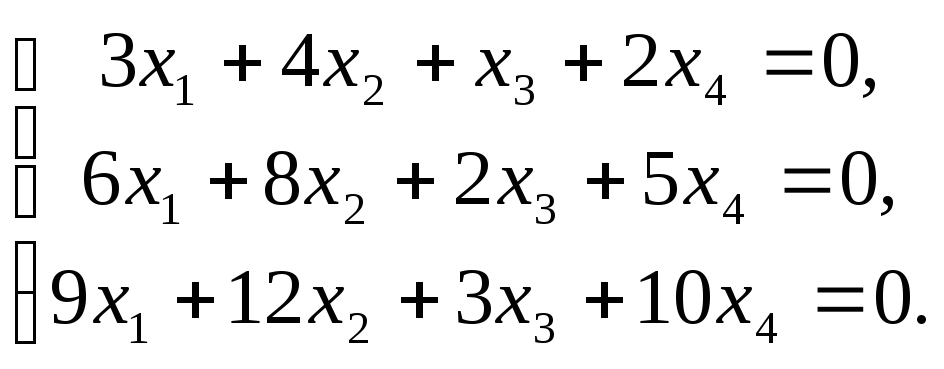 Найти общее решение и одно частное.
Найти общее решение и одно частное.
Решение:
1). Составим матрицу:
![]() =
=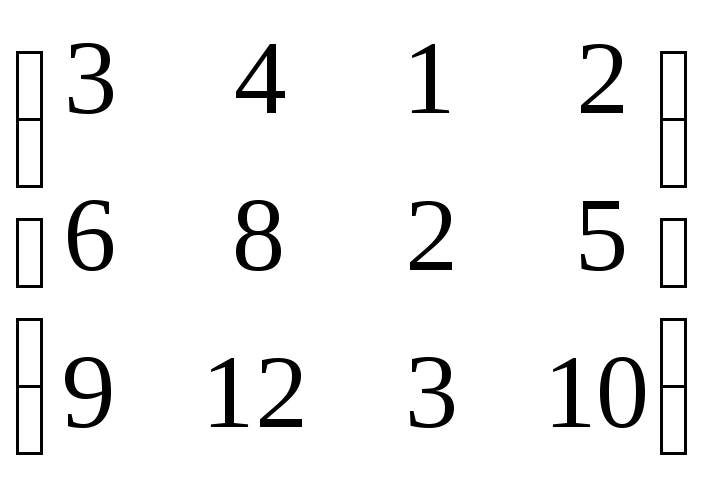 и найдём её ранг. Выделим для окаймления
минор (не равен нулю), расположенный в
правом верхнем углу матрицы:
и найдём её ранг. Выделим для окаймления
минор (не равен нулю), расположенный в
правом верхнем углу матрицы:
-
3
4
1
2
6
8
2
5
1
9
12
3
10
2
1
3). Окаймляющие
миноры будем обозначать:
![]() ,
где
,
где![]() –
указывает номер отмеченной для окаймления
строки,
–
указывает номер отмеченной для окаймления
строки,![]() –
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
–
указывает номер отмеченного для
окаймления столбца. Тогда можем записать:
![]() =
=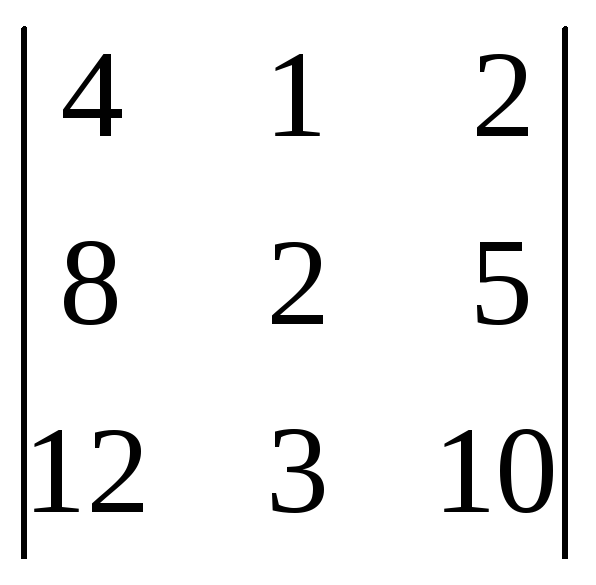 =4·
=4·![]() –8·
–8·![]() +12·
+12·![]() =m1·(5)–h1·(4)+g1·(1)=4·(5)–8·(4)+12·(1)
=0;
=m1·(5)–h1·(4)+g1·(1)=4·(5)–8·(4)+12·(1)
=0;
Замечание:
параметры: m1,
h1,
g1
изменяются при переходе к минорам
![]() ,
,![]() ,
числа:(5),
(4),
(1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
,
числа:(5),
(4),
(1)
не
изменяются. Это позволяет применить
единый шаблон вычислений!
![]() =
=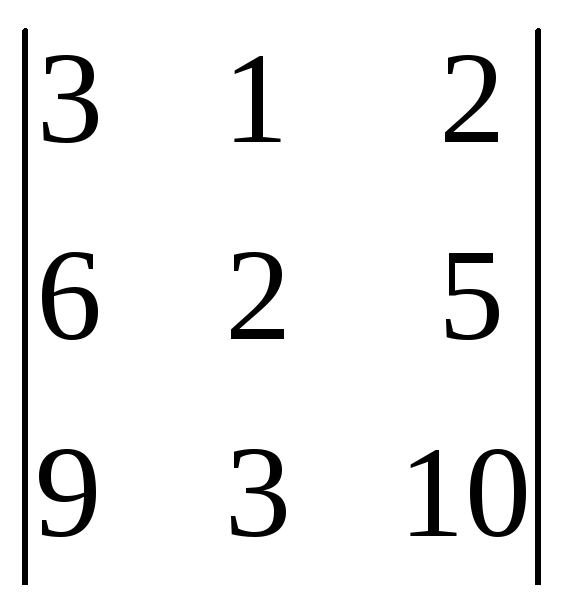 =
m2·(5)–h2·(4)+g2·(1)=
3·(5)–6·(4)+9·(1)
=0;
=
m2·(5)–h2·(4)+g2·(1)=
3·(5)–6·(4)+9·(1)
=0;
4).
Так как все миноры 3-го порядка
оказались равными нулю, то
![]() =2.
=2.
5). Учитывая
расположение не равного нулю минора,
3-е уравнение отбрасываем и свободными
неизвестными объявляем
![]() и
и![]() :
:
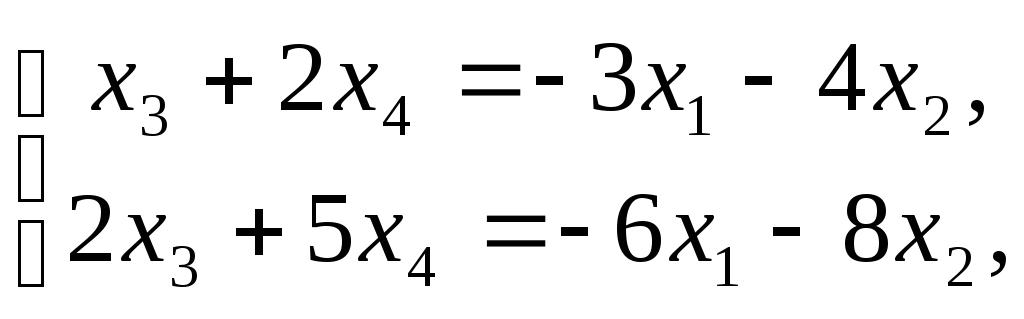
далее применяем правило Крамера:
![]() =1;
=1; ![]() =
=
![]() =
=![]() ;
;
![]() =
=![]() =0.
=0.
6). Общее решение
системы:
![]() =
=![]() =
=![]() ;
;
![]() =
=![]() =0;
частное решение получим при значениях:
=0;
частное решение получим при значениях:![]() =1,
=1,![]() =–1,
→
=–1,
→![]() =1,
=1,![]() =0.
=0.
Ответ:
общее решение:![]() =
=![]() =
=![]() ;
;
![]() =
=![]() =0;
частное решение: (1,–1,1,0).
=0;
частное решение: (1,–1,1,0).
Замечание: этот пример иллюстрирует алгоритм вычисления общего и одного частного решений, после чего определение ФСР становится достаточно простым завершением решения системы линейных однородных уравнений.
Пример–2:Найти общее решение
системы уравнений:
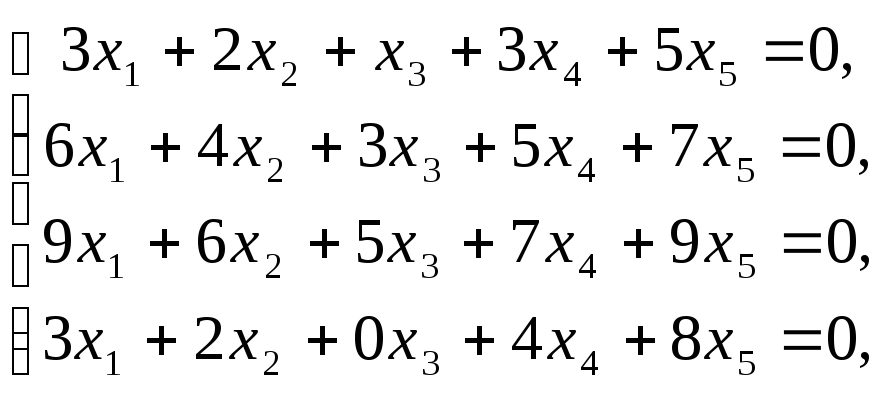 и ФСР.
и ФСР.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
3
2
1
3
5
3
2
1
3
5
6
4
3
5
7
0
0
1
-1
-3
9
6
5
7
9
=(1)→
0
0
2
-2
-6
=(2)→
3
2
0
4
8
0
0
-1
1
3
-
3
2
1
3
5
3
2
2
2
2
0
0
1
-1
-3
0
0
1
-1
-3
0
0
0
0
0
=(3)→
0
0
0
0
0
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R4]–[R1]; [R2]–[R1]·2; [R3]–[R1]·3. (2): [R3]–[R2]·2; [R4]–[R2]. (3): [R1]–[R2]. (4): раскрываем полученный результат.
2).
Видим:
![]() =2.
Свободными неизвестными объявляем
=2.
Свободными неизвестными объявляем![]() ,
,![]() ,
,![]() .Раскрываемтаблицу:
.Раскрываемтаблицу:
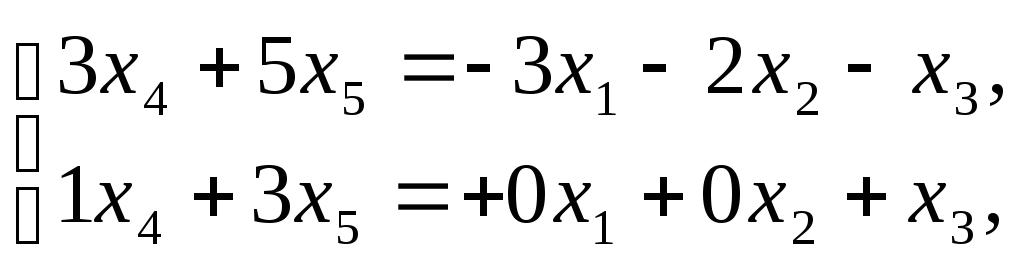
3) Применяем правило Крамера:
![]() =
4;
=
4;![]() =
=![]() =
=![]() ;
;
![]() =
=![]() =
=![]() .
.
4). Общее решение
системы: x4=![]()
![]() ;
x5=
;
x5=![]()
![]() .
.
5). Построим ФСР (фундаментальную систему решений), избегая дробей:
-
x1
x2
x3
x4
x5
α1
4
0
0
9
-3
α2
0
4
0
6
-2
α3
0
0
4
8
-4
Векторы-решения
![]() ,
,![]() ,
,![]() линейно независимы, их количество
линейно независимы, их количество![]() =3.
Эти векторы могут быть приняты в качестве
ФСР.
=3.
Эти векторы могут быть приняты в качестве
ФСР.
Ответ: общее
решение: x4=![]()
![]() ;
x5=
;
x5=![]()
![]() ;
;
ФСР:
![]() =
(4, 0, 0, 9,–3) ;
=
(4, 0, 0, 9,–3) ; ![]() =
(0, 4, 0, 6, –2) ;
=
(0, 4, 0, 6, –2) ; ![]() =
(0, 0, 4, 8, –4).
=
(0, 0, 4, 8, –4).
Пример–3:Найти общее решение
системы уравнений:
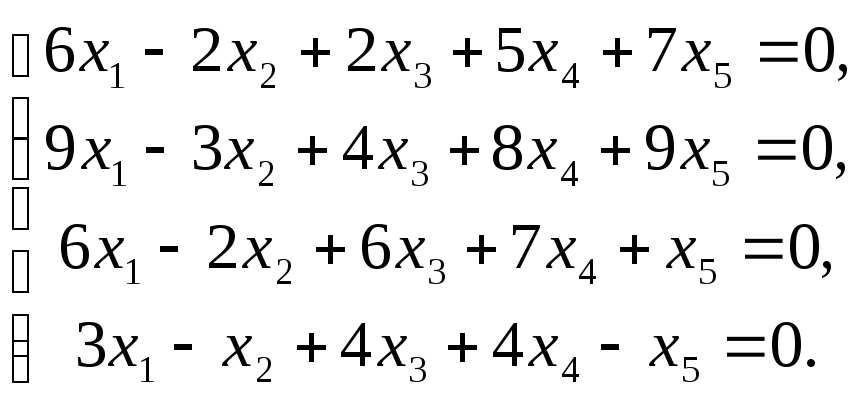 и ФСР.
и ФСР.
Решение:
1). Применим пошаговый процесс метода Гаусса:
-
6
-2
2
5
7
6
-2
2
5
7
9
-3
4
8
9
3
-1
2
3
2
6
-2
6
7
1
=(1)→
0
0
2
1
-3
=(2)→
3
-1
4
4
-1
0
0
2
1
-3
-
3
-1
0
2
5
3
-1
0
2
5
0
0
2
1
-3
0
0
2
1
-3
0
0
2
1
-3
=(3)→
0
0
0
0
0
=(4)→
0
0
0
0
0
0
0
0
0
0
Выполнены операции: (1): [R2]–[R1]; [R3]–[R1]; делим [R3] на число 2; [R4]–[R2]. (2): [R1]–[R2]; [R4]–[R3]; [R2]–[R1];. (3): [R3]–[R2]. (4): раскрываем полученный результат.
2).
Видим:
![]() =2.
Свободными неизвестными объявляем
=2.
Свободными неизвестными объявляем![]() ,
,![]() ,
,![]() .
.
3). Раскрывая
таблицу, из уравнения [R2]
вычисляем:![]() =
=![]() ;
из уравнения [R1]
вычисляем:
;
из уравнения [R1]
вычисляем: ![]() =
=![]() . Получено общее
решение: как и в случае неоднородной
системы уравнений.
. Получено общее
решение: как и в случае неоднородной
системы уравнений.
4). Построим ФСР, избегая дробей в записи решений ФСР:
-
x1
x3
x2
x4
x5
α1
2
0
6
0
0
α2
-4
-3
0
6
0
α3
-10
9
0
0
6
Векторы-решения
![]() ,
,![]() ,
,![]() линейно независимы, их количество
линейно независимы, их количество![]() =2.
Эти векторы могут быть приняты в качестве
ФСР.
=2.
Эти векторы могут быть приняты в качестве
ФСР.
5).
Используя ФСР, запишем общее решение:![]() =
=![]() +
+![]() +
+![]() .
Такая запись общего решения невозможна
для неоднородной системы!
.
Такая запись общего решения невозможна
для неоднородной системы!
Ответ: общее
решение:
![]() =
=![]() ;
;![]() =
=![]() ;
или:
;
или: ![]() =
=![]() +
+![]() +
+![]() .
.
ФСР:
![]() =
(2, 0, 6, 0,0) ;
=
(2, 0, 6, 0,0) ; ![]() =
(–4,–3, 0,6 ,0);
=
(–4,–3, 0,6 ,0); ![]() =
(–10,9, 0, 0,6).
=
(–10,9, 0, 0,6).
Варианты индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
Вар. |
Задание: |
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|
6.4. Решить систему неоднородных линейных уравнений, записав его общее решение в виде суммы частного решения неоднородного уравнения и общего решения присоединённой однородной системы.
Общие сведения и расчётные формулы:для выполнения задания достаточно следовать алгоритму решения, представленному в примере.
Пример–1:Решить систему
уравнений:
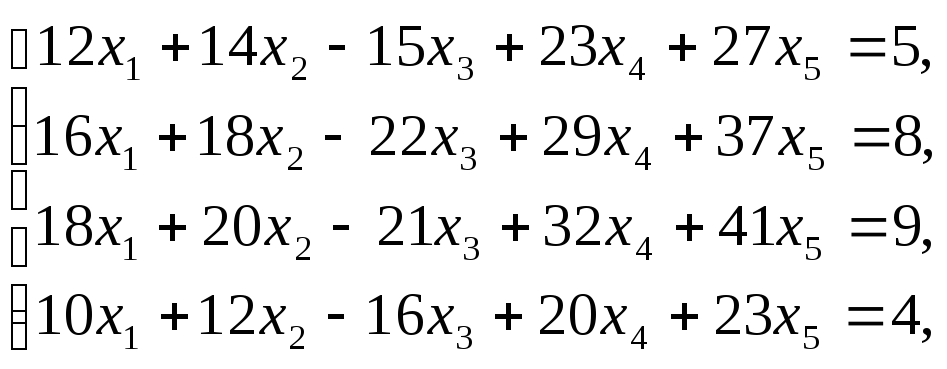 записав общее решение в виде суммы
частного решения неоднородного уравнения
и общего решения присоединённой
однородной системы.
записав общее решение в виде суммы
частного решения неоднородного уравнения
и общего решения присоединённой
однородной системы.
Решение:
1). Полное исследование системы позволяют провести как метод Гаусса, так и алгоритм в соответствии с теоремой Кронекера-Капелли. Применим пошаговый процесс метода Гаусса:
|
12 |
14 |
-15 |
23 |
27 |
5 |
|
|
2 |
2 |
1 |
3 |
4 |
1 |
|
|
16 |
18 |
-22 |
29 |
37 |
8 |
|
|
0 |
2 |
-30 |
5 |
5 |
0 |
|
|
18 |
20 |
-21 |
32 |
41 |
9 |
=(1)→ |
2 |
2 |
1 |
3 |
4 |
1 |
=(2)→ | |
|
10 |
12 |
-16 |
20 |
23 |
4 |
|
|
0 |
2 |
-21 |
5 |
3 |
-1 |
|
|
2 |
2 |
1 |
3 |
4 |
1 |
|
|
|
0 |
2 |
-30 |
5 |
5 |
0 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
=(3)→ | |
|
0 |
0 |
9 |
0 |
-2 |
-1 |
|
|
Выполнены операции: (1): [R1]–[R4]; [R3]–[R2]; [R2]–[R1]·8; [R4]–[R1]·5. (2): [R3]–[R1]; [R4]–[R2]. (3): обрабатываем результаты.
2). Получены результаты: - система совместна;
- ранг системы
равен 3; свободные неизвестные:
![]() и
и![]() :
:
- раскрываем строки преобразованной системы:
из уравнения [R4]:
![]() =
=![]() ;
из уравнения[R2],
с учётом найденного значения неизвестной
;
из уравнения[R2],
с учётом найденного значения неизвестной
![]() :
:
![]() =
=![]() ;
из уравнения[R1],
с учётом найденных значения неизвестных
;
из уравнения[R1],
с учётом найденных значения неизвестных
![]() и
и ![]() :
:
![]() =
=![]() .
.
3). Частное решение
системы найдём при условии, что свободным
неизвестным присвоили значения
![]() =1,
=1,![]() =1
=1![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() ,
обозначим его:
,
обозначим его: ![]() =
=![]() .
.
4). Общее решение
присоединённой однородной системы:
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() =
=![]() .
Построим ФСР (фундаментальную
систему решений):
.
Построим ФСР (фундаментальную
систему решений):
-
x1
x2
x3
x4
x5
α1
2
-5
0
2
0
α2
-53
15
4
0
18
Векторы-решения
![]() ,
,
![]() линейно независимы, их количество
линейно независимы, их количество![]() =2.
Эти векторы могут быть приняты в качестве
ФСР.
=2.
Эти векторы могут быть приняты в качестве
ФСР.
5). Общее решение
системы:
![]() =
=![]() +
+![]() =
=![]() +
+![]() +
+![]() .
.
Ответ: общее
решение:
![]() =
=![]() +
+![]() +
+![]() .
.
Варианты индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
Вар. |
Задание: |
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|