Часть 1. Дифференциальные уравнения (ду) 1-го порядка.

ЗАНЯТИЕ 3. Постановка задачи Коши (для ДУ 1-го порядка). Составление ДУ для заданного уравнения семейства кривых линий. Изоклины. Решение уравнений с разделяющимися переменными.

Ауд.

Л-4. Гл. 10

№ 9, 18, 22-34 (чётные), 40, 44.

11

☺ ☻ ☺

Основные понятия:

1. Дифференциальным уравнением (ду) называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы).

2. Решить ду – значит найти все его решения!

3. Решение ду – любая функция, которая, будучи подставлена в исходную запись уравнения, обращает его в тождество!

••• ≡ •••

Пример 2–18: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: = –.

Р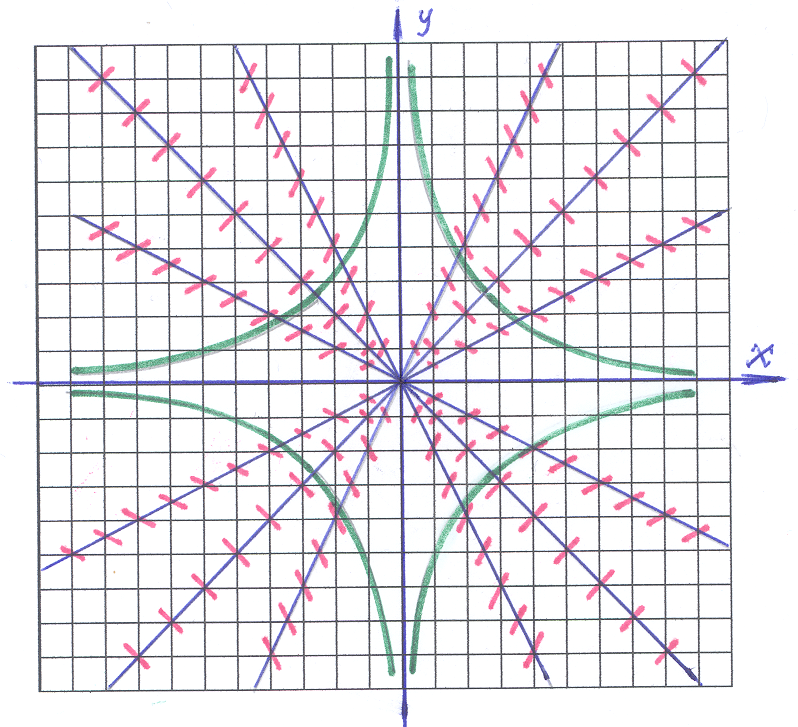ешение:

1). Уравнение изоклин получается приравниванием =k. В нашем случае изоклина – прямая линия: . На рисунке изоклины выделены «синим» цветом. На каждой изоклине черточка («красная») отражает конкретное значение k, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.

2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемые «интегральные кривые» (на рисунке интегральные кривые выделены «зеленым» цветом), то есть «решение» заданного ДУ.

Ответ: интегральная кривая представлена на рисунке.

Пример 3–22: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение очевидных решений не имеет. Запишем уравнение в виде: , видим – уравнение с разделяющимися переменными.

2). Интегрируем уравнение: =, или – общее решение дифференциального уравнения.

Ответ: – общее решение ДУ (семейство гипербол).

Пример 4–24: Решить дифференциальное уравнение: . (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: и .

2). Умножим исходное уравнение (1) на дифференциал . Уравнение (1) перепишем в дифференциальной форме: . (2)

3). Нетрудно заметить, что уравнение (2) есть уравнение с разделяющимися переменными. Интегрируем уравнение (2): +=, или . (3)

Ответ: – общее решение ДУ (семейство концентрических окружностей).

Пример 5–26: Решить дифференциальное уравнение: . (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) не может иметь решения в виде , в частности в виде функции . Это значит, что дифференциал не может быть равным 0. В то же время, функция =0 есть решение уравнения (1).

2). Умножим исходное уравнение (1) на дифференциал . Уравнение (1) перепишем в дифференциальной форме: . (2)

3). Нетрудно заметить, что уравнение (2) есть уравнение с разделяющимися переменными. Так как решение уже учтено, теперь примем, что и перепишем уравнение (2) в виде: +=0. (3)

4). Используя простейшие приёмы вычисления неопределённых интегралов, проинтегрируем уравнение (3). При получении общего решения уравнения (3) применим два принципиально разных способа использования произвольной постоянной величины:

→или . (4)

→или . (5)

Замечания: 1. При получении выражений (4) и (5) принципиальным было применение условия y≠0. При получении записи (5) также необходимо потребовать выполнения условия C≠0!..

2. Использование записи (5) удобнее в случае решения задачи Коши: вычисление постоянной C совсем просто, при использовании (4) пришлось бы применять логарифмы!.. Если общее решение уравнения воспринимать как совокупность кривых, то записи эквиваленты!..

Ответ: общее решение ДУ ; хотя при получении общего решения произвольная постоянная величина не должна принимать значение 0, формально из него можно получить решение исходного уравнения при значении .

Пример 6–28: Решить дифференциальное уравнение: . (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: и .

2). Умножим исходное уравнение (1) на дифференциал . Уравнение (1) перепишем в дифференциальной форме: . (2)

3). Теперь воспользуемся тем, что переменные в уравнении разделяются. Уравнение (2) можно записать в виде: . (3)

4). Интегрируем уравнение (3): =+, или – общее решение дифференциального уравнения.

Ответ: – общее решение ДУ.

Пример 7–30: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение очевидных решений не имеет. Запишем уравнение в виде: +2=0 (умножение на число 2 удобно!), видим – уравнение с разделяющимися переменными → можно приступить к интегрированию ДУ.

2). Интегрируем: – общее решение ДУ.

Ответ: – общее решение ДУ.

Пример 8–32: Решить дифференциальное уравнение: . (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) имеет решения в виде функции: , то есть ось .

2). Теперь воспользуемся тем, что переменные в уравнении (1) разделяются. Перепишем это уравнение в виде: =. (2)

3). Интегрируем: =, или – общее решение дифференциального уравнения, или (лучше!) в виде .

Ответ: – общее решение ДУ, также: y = 0 (выделяется из общего при =0).

Пример 9–34: Решить дифференциальное уравнение: . (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) имеет решения в виде функции: , прямая, параллельная оси .

2). Преобразуем уравнение (1), учитывая, что теперь , а также =:

. (2)

3). Интегрируем: – общее решение ДУ.

Ответ: – общее решение ДУ, также: .

Пример 10–40: Решить дифференциальное уравнение: .

Решение:

1). Примем: . Учитывая, что , перепишем уравнение (1): . Из равенства имеем решения: =, где .

2). Интегрируем уравнение: , применяя подстановку: и учитывая выражения и . Интегрирование левой части: , правой: .

3). Учитывая, что и , запишем общее решение: .

Ответ: – общее решение ДУ, также: =, где .

Пример 11–44: Найти частное решение уравнения: , .

Решение:

1). Запишем заданное уравнение в виде: – уравнение с разделяющимися переменными.

2). Интегрируем: – общее решение ДУ.

3). Используя начальные условия, запишем: – частное решение ДУ.

Ответ: – частное решение ДУ.

Вопросы для самопроверки:

1. Какое уравнение называют дифференциальным?

2. Как определить порядок ДУ?

3. Что такое решение ДУ, частное решение ДУ?

4. Что такое общее решение ДУ?

5. Что значит решить Задачу Коши?

6. Что такое семейство кривых?

7. Как построить уравнение, решением которого является заданное семейство кривых?

8. Каковы стандартные формы ДУ с разделяющимися переменными?

9. Какова стандартная схема решения ДУ с разделяющимися переменными?

☺☺

ЗАНЯТИЕ 4. Линейные дифференциальные уравнения 1-го порядка и уравнения Бернулли.

Ауд.

Л-4. Гл. 10

№ 68-74 (чётные), 84, 86, 88, 94.

8

☺ ☻ ☺

Дифференциальное уравнение 1-порядка называют линейным, есливходящие в него искомая функцияи ее производнаявходят в уравнение в 1-й степени. Запись линейного уравнения считаемстандартной, если она имеет вид:, (1)

где и – непрерывные функции переменной или постоянные.

Для формы записи (1) используем стандартный алгоритм решения уравнения:

1. Решение уравнения ищем в виде функции:, гдеи.

2. Вычисляем интеграл:и записываем выражение:=.

3. Вычисляем:=, где произвольная постоянная величина, в зависимости от конкретных выражений для функцийи, может быть записана и в виде выражений,и др.

4. Запишем общее решение уравнения:=∙.

Замечание: Для того, чтобы формально (как предписанную технологию) применять стандартный алгоритм решения линейного уравнения, первым действием при решении линейного уравнения 1-го порядка всегда должно быть приведение конкретного уравнения к форме записи (1)!..

••• ≡ •••

Пример 1–68: Решить дифференциальное уравнение: .

Решение:

1). Приводим уравнение к стандартной форме: .

2). Вычисляем интеграл: ==. Тогда:==, или=.

Замечание: в последней записи выражения для функции знак модуля опущен, так как от функции требуется только обеспечить выполнение равенства: (это показано в Пособии при получении алгоритма решения линейного уравнения).

3). Вычисляем: ==+ =+.

4). Запишем общее решение уравнения: =∙=.

Ответ: = – общее решение.

Пример 1–70: Решить дифференциальное уравнение: .

Решение:

1). Запишем уравнение в форме: , где = и =.

2). Вычисляем интеграл: =–=. Тогда:==.

3). Вычисляем: ==+ =+.

4). Запишем общее решение уравнения: =∙.

Ответ: = ∙– общее решение.

Пример 2–72: Решить дифференциальное уравнение: .

Решение:

1). Уравнение соответствует стандартной форме: , отметим сразу, что переменная . Запишем также: и .

2). Вычисляем интеграл: ==и записываем выражение:==.

3). Вычисляем: ==+=++=++, или, после очевидных преобразований:=

Замечание: интеграл в таблице интегралов: =+. Его нетрудно получить методом интегрирования по частям.

4). Запишем общее решение уравнения: =∙=.

Ответ: =– общее решение.

Пример 4–74: Решить дифференциальное уравнение: =.

Решение:

1). Прежде всего, отметим, что исходное уравнение имеет очевидное решение .

2). Теперь принимаем и приводим уравнение к стандартной форме: .

Замечание: Переход от записи решения в виде функции к записи подсказан исходным выражением вполне выразительно!..

3). Решение уравнения ищем в виде функции: , гдеи.

4). Вычисляем интеграл: ==. Тогда:==, или=.

5). Вычисляем: ==+ =+.

6). Запишем общее решение уравнения: =∙=.

Ответ: = – общее решение. Из исходного уравнения также: – решение.

Пример 5–84: Найти частное решение ДУ: , удовлетворяющее условию: =.

Решение:

1). Запишем уравнение в стандартной форме: , где: и =.

2). Вычисляем интеграл: ==и записываем выражение:==.

3). Вычисляем: ==+=+, или, после очевидных преобразований:=+.

Замечание: интеграл в таблице интегралов: =+. Его нетрудно получить методом интегрирования по частям.

4). Запишем общее решение уравнения: =. Из условия =получаем значение=1. Запишем частное решение:=

Ответ: = – частное решение.

☺☺

Дифференциальные уравнения 1-порядка Бернулли:, (1)

где и – непрерывные функции переменной или постоянные, – произвольное число. Уравнение Бернулли интересно тем, что использованием стандартного приёма приводится к линейному уравнению, которое мы уже умеем решать!.. Вот этот приём:

1. Применим подстановку:и перепишем (1):.

2. Обозначив:=и=, запишем:– линейное уравнение в стандартной форме.

Замечание: Для того, чтобы формально (как предписанную технологию) применять стандартный алгоритм решения уравнения Бернулли, первым действием всегда должно быть приведение конкретного уравнения к форме записи (1)!..

••• ≡ •••

Пример 6–86: Решить дифференциальное уравнение: . (1)

Решение:

1). Уравнение (1) есть уравнение Бернулли в стандартной форме для значения, при этом имеем: и .

2). Применим подстановку: =и перепишем (1) как:, то есть:, или, где=,=.

3). Далее применяем стандартный алгоритм решения линейного уравнения: , записанного в стандартной форме, приняв.

4). Вычисляем интеграл: ==и записываем выражение:==.

5). Вычисляем: =+=+ ==+.

6). Запишем общее решение уравнения: =∙, или=∙.

Ответ: =∙– общее решение.

Пример 7–88: Решить дифференциальное уравнение: . (1)

Решение:

1). Из уравнения (1) следует: – решение. Запишем уравнение Бернулли в стандартной форме: . (2)

2). Отметим в уравнении (2) параметры: , = и =.

3). Применим подстановку: =и перепишем (2) как:, то есть:, или, где=,=.

4). Далее решаем линейное уравнение: , записанное в стандартной форме, приняв.

5). Вычисляем интеграл: ==и записываем:==.

6). Вычисляем: =+=+=.

7). Запишем общее решение уравнения: =∙. Если учесть, то получим:=∙, или∙∙=1.

Ответ: ∙∙=1 – общее решение уравнения, также .

Пример 8–94: Решить дифференциальное уравнение: , y=1. (1)

Решение:

1). Из уравнения (1) следует: и – решение. Разделив равенство (1) на , получим уравнение Бернулли в стандартной форме: . (2)

2). Отметим в уравнении (2) параметры: , и .

3). Применим подстановку: =и перепишем (2) как:, то есть:, или, где,=.

4). Далее применяем стандартный алгоритм решения линейного уравнения: , записанного в стандартной форме, приняв.

5). Вычисляем интеграл: ==и записываем:==.

6). Вычисляем: =+=+=+=.

7). Запишем общее решение уравнения: =∙=. Если учесть, то получим:.

8). Через точку проходит интегральная кривая: , так как =4.

Ответ: – общее решение уравнения, также ; частное: .

Вопросы для самопроверки:

1. Как определяют линейное дифференциальное уравнение 1-го порядка?

2. Что значит: «стандартная форма» линейного уравнения, зачем её вводят?

3. Какова основная «идея» способа «подстановки» решения линейного уравнения?

4. Всегда ли можно «проинтегрировать» линейное ДУ?

5. Какие уравнения относят к уравнениям Бернулли?

6. В чем особенность интегрирования уравнения Бернулли?

7. Бывают ли уравнения Бернулли, которые невозможно «проинтегрировать»?

☺☺

ЗАНЯТИЕ 5. Однородные функции двух переменных. Решение однородных дифференциальных уравнений первого порядка. Полный дифференциал функции двух переменных. Критерий Эйлера. Решение уравнений в полных дифференциалах.

Ауд.

Л-4. Гл. 10

№ 46-52 (чётные), 96-104 (чётные).

9

☺ ☻ ☺

Однородные функции и их использование в решениях однородных ДУ 1-порядка:

Функция называется однородной функцией порядка относительно переменных , если при любом верно: . В частном случае функция может оказаться такой, что . В этом случае, так как =1, говорят, что функция однородная нулевого порядка. Однородную функцию нулевого порядка можно представить в виде функции: =. Если функция однородная функция порядка относительно переменных , то её отношение к величине есть однородная функция нулевого порядка. В таком случае верно: =, что равносильно записи исходного определения: .

Однородные дифференциальные уравнения 1-порядка вида:. (1)

1). Запись (1) подсказывает, что исследуемый процесс определяется отношением величин и это отношение неплохо бы (подсказано!) назвать одной величиной:, то есть.

2). Так мы хотим, чтобы функция была решением уравнения (1), необходимо подставить её в исходное уравнение (по определению!)!.. Так как, после подстановкиив (1) получаем:, или (так как). (2)

3). Уравнение (2) есть уравнение с разделяющимися переменными! Исследуем равенство: . Если имеется такое число, что, то, илиесть решение уравнения (1).

4). Теперь примем: . Уравнение (2) запишем в виде:. Его интегрирование даёт общий интеграл (решение):. (3)

5). Будем считать, что интеграл в выражении (3) удалось вычислить: . Если в последнем заменить, получим общий интеграл уравнения (1):.

Однородные уравнения 1-порядка вида:. (4)

1). Если в записи (4) функции иоднородные одного порядка, то его легко преобразовать к виду (1).

2). Как всегда, сначала попробуем выделить решения уравнения, используя (4). Если при значении случится, то прямаяесть решение уравнения. Если при значениислучится, то прямаяесть решение уравнения.

3). Теперь и, уравнение (4) запишем в форме (1):. Далее по общему алгоритму!..

••• ≡ •••

Пример 1–46: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение не имеет очевидных решений.

2). Так как в заданном уравнении правая часть зависит только от отношения неизвестных, то это уравнение – однородное! Примем и запишем: =.

3). Вычислим интеграл ==. Для функцииполучено общее решение:

4). Для функции получено общее решение:, или учитывая, что, перепишем общее решение с использованием:.

Ответ: – общее решение ДУ.

Пример 2–48: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение не имеет очевидных решений. Перепишем его в виде: 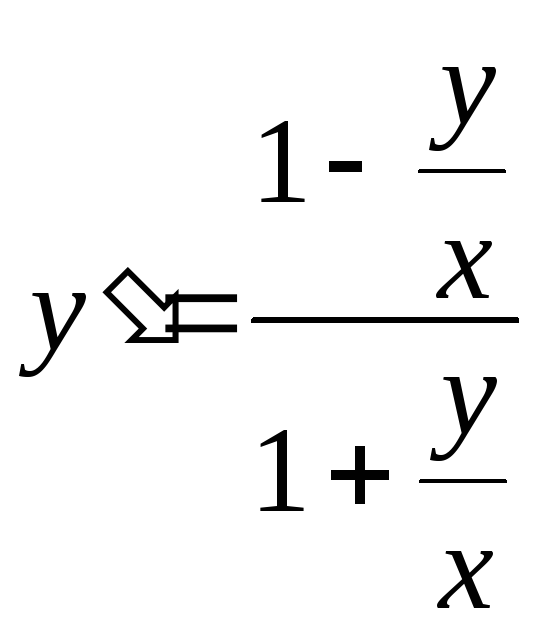− форма записи (1). В этой записи правая часть зависит только от отношения неизвестных, то это уравнение – однородное!

2). Примем и запишем: ==. Принимая: =0, выделяем решения: =0.

3). Теперь 0.Вычислим интеграл==. Для функцииполучено общее решение:

4). Для функции общее решение:=, или=. Учитывая, что, перепишем общее решение:=.

Ответ: = – общее решение ДУ, также =0 (его Задачник прозевал!).

Пример 3–50: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение имеет очевидное решение: =0. Уравнение записано в форме (4). Легко заметить, что это уравнение однородное.

2). Так как решение =0 учтено, примем: и . Запишем уравнение: − форма записи (1). Примем и запишем: ==.

3). В нашем случае . Вычислим интеграл==.

4). Для функции получено общее решение:=, или. Учитывая, что, перепишем общее решение использованием:.

Ответ: – общее решение ДУ, также: =0 (из общего не выделяется ни при каком ).

Пример 4–52: Решить дифференциальное уравнение: .

Решение:

1). Прежде всего, отметим, что исходное уравнение не имеет очевидного решения. Легко заметить, что это уравнение однородное.

2). Запишем уравнение: − форма записи (1). Примем и запишем: ==.

3). В нашем случае . вычислим интеграл==.

4). Для функции получено общее решение:=. Учитывая, что, перепишем общее решение использованием:=, или.

Ответ: = – общее решение ДУ, или .

☺☺

Дифференциальное уравнение 1-порядка называют уравнением в полных дифференциалах, есливходящие в него функцииинепрерывны и дифференцируемы, а также выполняется условие:=, причём частные производныеи– непрерывные функции в некоторой области.

Для решения дифференциального уравнения в полных дифференциалах используем стандартный алгоритм:

1. Проверяем выполнение условия:=. Если условие выполняется, то заданное уравнение есть уравнение в полных дифференциалах. Решение ищем в виде функции.

2. Имея функцию=, находим функцию:=+, гдеотражает ту часть функции, которая была потеряна при дифференцировании:. Для удобства обозначим:=.

3. Функциюнаходим из условия=, или+=. Для этого необходимо проинтегрировать:=–, то есть вычислить интеграл:=.

4. Запишем решение:=+=.

••• ≡ •••

Пример 5–96: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: =1 и =1 → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: =и запишем условие:=–. Для заданного уравнения:==.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас:+=.

Ответ: += – общее решение.

Пример 6–98: Решить дифференциальное уравнение: , предварительно убедившись, что оно является уравнением в полных дифференциалах.

Решение:

1). Проверим выполнение условия: =. У нас: = и = → заданное уравнение есть уравнение в полных дифференциалах.

2). Вычислим интеграл: ===.

3). Вычислим производную: =и запишем условие:=–. Для заданного уравнения:==.

4). Вычислим интеграл: ===.

5). Запишем решение: =+=. У нас:=.

Ответ: = – общее решение.

Замечания: 1). Пример интересен тем, что заданное ДУ можно отнести и к однородным уравнениям: функции и – однородные порядка 2. Если попробовать решать его по схеме однородного уравнения, то трудоёмкость процесса возрастет в разы: f(u)–u=–u= → J=.

2). Ещё большим будет интерес, если обратить внимание на ситуацию возможного равенства: =0. По основной теореме алгебры мы получим три корня: , , → получаем дополнительно три решения ДУ: , , – прямые, проходящие через начало координат.