
Высшая математика
.pdf
5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
y
1 2 |
x |
-4 -6
-8
Рис.4
5.15.6. Точки перегиба графика функции
Предположим, что график функции y=f(x) имеет определенное направление выпуклости на каждом из интервалов (а,с) и (с,b), где числа а,b,c связаны неравенствами a<c<b. Предположим, что к графику функции y=f(x) в точке М(с,f(c)) cуществует касательная не параллельная оси OY, тогда точка М(с,f(c)) графика функции y=f(x) называется точкой перегиба этого графика, если существует такая окрестность точки С оси абсцисс, в пределах которой график функции y=f(x) слева и справа от точки С имеет разные направления выпуклости (см.рис.1)
y
•M
c x
Теорема 1. (необходимое условие существования точки перегиба).
Пусть график функции y=f(x) имеет перегиб в точке М(с,f(c)) и функция y=f(x) имеет в
точке С непрерывную вторую производную тогда f ′′(с)=0.
Рис.1
Замечание1. Равенство нулю второй производной не является достаточным условием перегиба. Например, для функции y=x4 в точке (0,0) нет перегиба, однако y′′(0) =12x2 x=0 = 0 . (см. рис. 2)
Замечание 2. Все точки перегиба дважды непрерывно
yдифференцируемой функции находятся среди точек, для которых вторая производная равна нулю.
0 x
Рис. 2
5.15.7. Теоремы о достаточных условиях перегиба графика функции
Теорема 1. (первое достаточное условие перегиба). Пусть функция f(x)
1) имеет вторую производную в некоторой окрестности точки С;
141
5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
2) f ′′(с) = 0, тогда, если существует окрестность, в пределах которой вторая производная f ′′(x) имеет разные знаки слева и справа от точки C, то график этой функции имеет перегиб в точке М(с,f(с)).
Замечание 1. Сформулируем обобщение теоремы 1. При определении точки перегиба будем считать, что касательная к графику функции в рассматриваемой точке может
быть параллельной оси 0y (т.е.f ′(с) = ±∞).
Пусть функция f(x): 1) имеет конечную вторую производную всюду в некоторой окрестности точки С, за исключением, быть может, самой точки С; 2) функция f(x) непрерывна в точке С; 3) график функции имеет касательную в точке М(с,f(с)) (может быть и параллельно оси 0y). Тогда, если существует окрестность точки С, в пределах которой
f ′′(x) имеет разные знаки слева и справа от точки С, то график функции y=f(x) имеет пе-
региб в точке М(с,f(с)).
Замечание 2.
y |
y |
M
M 
Пункт 2 в условии теоремы исключает случай, приведенный на рис. 1, а пункт 3 – на рис. 2 (слева от точки С график функции касается прямой х=С в точке М, а справа касания нет)
C x C x
Рис. 1 Рис. 2
Пример. |
Найти точки перегиба графика функции y = 3 |
x . |
|
||||
|
|
Так как y′(x)= |
1 , то в точке х=0 y′ = +∞и график |
||||
y |
|
33 |
x2 |
|
|
||
|
функции касается в точке (0,0) оси ОУ. y′′(x) = − |
2 и |
|||||
|
|
||||||
|
|
поэтому y′′(x) > 0 при x < 0 и |
93 |
x5 |
|||
|
|
y′′ < 0 при x > 0 , а в точ- |
|||||
0 |
x |
ке х=0 y′′(x) |
|
x=0 = ∞ . |
|
|
|
|
|
|
|||||
Рис. 3
Отсюда следует, что точка (0,0) является точкой перегиба; слева от этой точки график функции имеет выпуклость вниз, а справа вверх.
5.15.8. Асимптоты графика функции
Определение 1. Прямая х=а называется вертикальной асимптотой графика функ- |
|||
ции y=f(x), если хотя бы одно из предельных значений lim f(x) |
и |
lim f(x) |
равно +∞ |
x→a +0 |
|
x→a-0 |
|
или −∞.
142

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
y |
Пример. y = |
1 |
. Так как |
lim |
1 |
= −∞ и |
lim |
1 |
= +∞, |
x |
|
|
|||||||
|
|
|
x→0−0 x |
|
x→0+0 x |
|
|||
x
то прямая х=0 – вертикальная асимптота графика функции y = 1x . (см. рис. 1)
Рис. 1
Определение 2. Пусть функция y=f(x) определена для всех x>a (x<a). Прямая
Y=kx+b называется наклонной асимптотой графика функции y=f(x) при х→ + ∞ (х→ − ∞), если функция f(x) представима в виде
f(x) = kx + b +α(x), г де lim α(x) |
= 0 |
(lim α(x) = 0). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x→+∞ |
|
|
|
x→−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Для того, чтобы график функции y=f(x) имел при х→ + ∞ (х→ −∞) на- |
|||||||||||||||||||||||||||
клонную асимптоту, необходимо и достаточно, чтобы существовали два предела: |
|
||||||||||||||||||||||||||
|
f(x) |
|
|
|
|
f(x) |
|
|
|
|
|
(x) |
|
|
] |
|
|
|
|
f(x)− kx |
] |
|
) |
|
|
||
lim |
|
= k lim |
|
= k и |
lim |
f |
− kx |
= b |
lim |
= b |
. |
|
|||||||||||||||
x |
x |
|
|||||||||||||||||||||||||
x→+∞ |
|
x→−∞ |
|
|
|
x→+ ∞[ |
|
|
|
|
|
|
|
(x→−∞[ |
|
|
|
|
|
||||||||
Доказательство. Необходимость. Пусть график функции y=f(x) имеет асимптоту, |
|||||||||||||||||||||||||||
для |
определенности, |
при |
х→ + ∞, |
т.е. f(x) может |
быть представлена |
в виде |
|||||||||||||||||||||
f(x) |
= kx + b +α(x), lim α(x) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
kx + b +α(x) |
|
|
|
|
b |
|
α(x) |
|
|
|
|
|
|
|
|
|
||||||
lim |
|
= |
lim |
|
|
|
|
|
= |
lim k |
+ |
|
+ |
|
|
|
= k |
|
|
|
|
|
|
|
|
||
x |
|
|
x |
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|||||||||||
x→+∞ |
|
x→+∞ |
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim [f(x)− kx] |
= lim [b |
+α(x)]= b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→+∞ |
|
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
|
|
||
Достаточность. |
Пусть |
существует |
|
lim |
|
= k |
и |
lim [f(x)− kx]= b , |
тогда |
||||||||||||||||||
|
|
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→+∞ |
|
|
|
x→+∞ |
|
|
|
|
|
||||
f(x)−kx=b+α(x) и |
lim α(x) = 0 . Отсюда следует, что f(x)=kx+b+α(x), где α(x) – бесконеч- |
||||||||||||||||||||||||||
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
но малая функция при х→ + ∞.
Замечание. Расположение графика относительно асимптоты при больших х определяется знаком разности ∆=f(x)−kx−b
∆>0 |
∆<0 |
∆ меняет знак при |
|
|
сколь угодно больших х. |
При х→ − ∞ аналогично
143

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
∆>0 |
∆<0 |
∆ меняет знак при |
|
|
сколь угодно больших по |
|
|
абсолютной величине х. |
Расположение графика относительно вертикальных и наклонных асимптот позволяет проверить исследование функции на экстремум, а также на направление выпуклости графика.
5.15.9. Примеры построения графиков функций
Будем проводить построение графиков функций, последовательно отвечая на вопросы, сформулированные ниже.
1. Построить график функции y = x2 (x −4)2
1.Область определения: −∞ < х < +∞;
2.Периодичность: функция не периодическая;
3. Четность: функция не является ни четной, ни нечетной, поскольку f(x)≠ f(-x) и f(x)≠ -f(- x);
4. Точки пересечения с осями ОХ и OY.
|
x = 4 |
x = 0 |
|
x = 0 |
; |
||
с осью ОХ: |
|
с осью OY: |
|
y = 0 |
y = 0 |
y = 0 |
|
5.Непрерывность: функция непрерывна х (−∞,+∞);
6.Асимптоты: функция не имеет ни вертикальных, ни наклонных асимптот;
7.Участки монотонности функции, нахождения экстремума.
y′(x) = 2x(x −4)2 +2x2 (x −4) = 2x(x −4)(x + x −4) = 4x(x −4)(x −2)
Стационарные точки функции: х1=0, х2=2, х3=4. Составим таблицу
x |
(-∞, 0) |
0 |
(0, 2) |
2 |
(2, 4) |
4 |
(4, ∞) |
y′ |
— |
0 |
+ |
0 |
— |
0 |
+ |
|
|
|
|
|
|
|
|
Рис. |
|
лок. |
|
лок. |
|
лок. |
|
|
|
мин. |
|
макс. |
|
мин. |
|
y |
|
0 |
|
16 |
|
0 |
|
|
|
|
|
|
|
|
|
Здесь 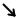 и
и  означают убывание и возрастание функции на соответствующих промежутках.
означают убывание и возрастание функции на соответствующих промежутках.
Примерный график функции представлен на рис.1.
144
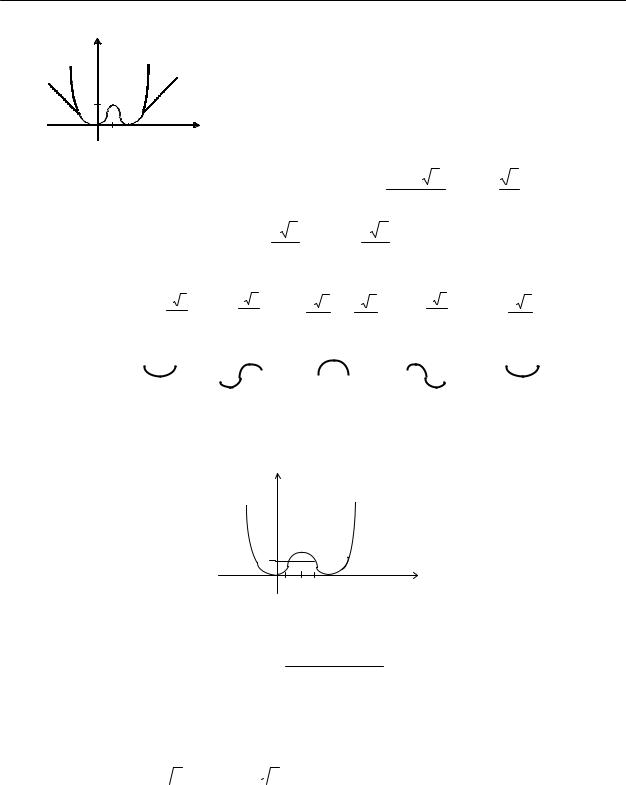
5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
y
1
0 |
2 4 |
x |
8. Нахождение точек перегиба: участки выпуклости
вверх и вниз графика функции. Вычисляем y′′(x). y′′(x)= 4[(x −2)(x −4)+ x(x −4)+ x(x −2)]=
= 4(x 2 −6x +8 + x 2 −4x + x 2 −2x)== 4(3x 2 −12x +8)
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(3± 3) |
|
|
|
|
|
|
|
|||||||
Приравняем нулю y′′(x):3x2 −12x +8 = 0; x |
|
|
= − |
|
|
|
3 |
|
|||||||||||||||||||||||||||||||
|
|
= 2 1± |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом y′′(x) |
|
|
|
|
|
|
+ |
2 |
3 |
|
|
|
|
|
− |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= 4 x −2 |
x −2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Составим таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
|
|
− |
2 3 |
|
|
2 |
− |
2 3 |
|
|
|
2 − |
2 3 |
,2 |
+ |
2 3 |
|
|
|
2 |
+ |
2 3 |
|
|
2 |
+ |
2 3 |
|
||||||||||
|
|
−∞,2 |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
,+∞ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y′′ |
|
|
+ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
— |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. |
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
Окончательный график функции представлен на рис. 2.
y
4
9 
0 x2 2 x1 x
Рис. 2
3.Построить график функции y = x3 + x2 −3x +1
x2 −1
1.Область определения: х≠±1.
2.Четность: функция не является ни четной, ни нечетной.
3.Периодичность: функция не является периодической.
4.Точки пересечения с осями координат: x3 + x2 −3x +1 = 0
x1 =1, x2 = −1−  2, x3 = −1+
2, x3 = −1+  2
2
Так как х≠ 1, то точки пересечения
145

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x = −1− |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3x+1 |
|
|
|
x-1 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 x = −1+ |
|
|
|
|
|
|
|
|
|
|
|
x |
|
+x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
C осью ОХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = 0 |
|
|
|
|
|
|
y = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
-x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+2x-1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2-3x+1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
С осью OY |
|
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x2-2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-x+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-x+1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
5. Непрерывность: функция имеет разрывы в точках х=±1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Исследуем характер точек разрыва |
|
|
|
|
|
|
|
|
|
x −1 |
|
|
x |
|
|
|
+2x −1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
+ x |
2 |
−3x |
+1 |
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
)( |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
= |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= +∞ |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
(x −1)(x +1) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x→−1−0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−1−0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
х=-1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+2x −1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
+ x |
2 |
−3x |
+1 |
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
= |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −∞ |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x +1) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x→−1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−1+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Точка х=-1 – точка разрыва 2-го рода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Пусть х=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
x3 + x2 −3x +1 |
= lim |
|
|
x2 +2x −1 |
=1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 −1 |
|
|
|
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1±0 |
|
|
|
|
|
|
|
|
|
x→±0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Точка х=1 – точка устранимого разрыва. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
6. Асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
х=−1 – вертикальная асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Наклонные асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
f(x) |
|
|
x3 + x2 −3x +1 |
|
|
|
1+ |
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
k = lim |
= lim |
|
= lim |
x |
|
x2 |
|
|
x3 |
=1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
( |
|
|
2 |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x→∞ |
|
|
|
|
x→∞ |
|
|
|
x x |
|
−1 |
|
|
|
|
|
x→∞ |
|
|
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b = lim[f(x)− kx] |
|
|
|
|
|
|
|
x3 + x2 − |
3x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 + x2 |
−3x +1− x |
3 + x |
|
|||||||||||||||||||||||||||||||||||||||||||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x |
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
2 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
−1 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x2 |
−2x +1 |
|
|
|
|
|
|
(x −1)2 |
|
|
|
|
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= lim |
= lim |
|
|
|
|
|
|
|
|
|
= lim |
x |
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(x −1)(x +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
x→∞ |
|
|
x2 −1 |
|
|
|
x→∞ |
|
|
|
x→∞ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Уравнение наклонной асимптоты у=х+1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
7. Участки монотонности, локальный экстремум функции. |
|
|
|
|
|
|
|
−3x +1)2x = |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y′ = |
x |
|
+ x |
|
−3x +1 |
= (3x |
|
+ |
2x −3)(x |
|
|
−1)−(x |
|
|
+ x |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x |
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 2 − |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
(3x 2 |
+ 2x −3)(x −1)(x |
+1)−2x(x −1)(x 2 + |
2x −1) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −1)2 (x +1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
146

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
|
3x 3 |
+5x 2 |
− x −3 −2x 3 −4x 2 + 2x |
|
x3 + x 2 + x −3 |
|
(x −1)(x 2 + 2x +3) |
|
|
||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
= |
||||
|
|
|
|
|
|
|
(x −1)(x +1)2 |
|
|
(x −1)(x +1)2 |
(x −1)(x +1)2 |
||||||||||||||||
|
|
|
3 2 |
|
|
|
x-1 |
|
|
|
|
Итак, y′(x) = |
x2 +2x +3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
x +x +x-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x +1)2 |
|
|
|
|||||
|
|
|
x3-x2 |
|
|
|
x2+2x+3 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2x2+x-3 |
|
|
|
|
|
|
|
|
|
Отсюда следует, что x y′(x) ≠ 0 |
||||||||||
|
|
|
|
|
|
2x2-2x |
|
|
|
|
|
|
|
|
|
ных точек функция не имеет. |
|
|
|||||||||
|
|
|
|
|
|
|
|
3x-3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При х=−1 y′(x) не существует. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3x-3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим таблицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
(-∞, -1) |
|
-1 |
|
|
|
(-1, ∞) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
y′ |
|
+ |
|
|
|
не сущ. |
|
+ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Рис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 + 2x +3
(x +1)2
и стационар-
8. Нахождение точек перегиба; участки выпуклости вверх и вниз графика функции.
|
x2 + 2x +3 |
′ |
(2x + 2)(x +1)2 −(x2 + 2x +3)2(x +1) |
|
|||||||||
y′′(x)= |
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
2 |
|
|
|
|
4 |
|
|
|
||||
|
|
(x +1) |
|
|
|
|
|
(x +1) |
|
|
|
|
|
= |
2(x +1)2 |
−2(x2 + 2x +3) |
= 2 |
x2 |
−2x +1− x2 −2x −3 |
= − |
|
|
4 |
||||
|
|
(x +1)3 |
|
|
|
|
(x +1)3 |
(x +1)3 |
|||||
y′′(x)> 0 x (−∞,−1) и y′′(x)< 0 x (−1,∞)
Составим таблицу
|
|
|
x |
|
(-∞, -1) |
|
|
|
|
-1 |
|
(-1, ∞) |
|||||||||
|
|
|
y′′ |
|
+ |
|
|
|
|
|
|
|
не сущ. |
|
— |
||||||
|
|
|
Рис. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График функции |
y = |
x3 |
+ x2 |
−3x +1 |
приведен на рис. 4 |
|
|||||||||||||||
|
3x2 |
−1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1- 2 1 |
|
|
1+ 2 1 2 |
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4
147

6.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
6.Неопределенный интеграл
6.1. Первообразная функция
Пусть функция f(x) определена на множестве М, которое является либо интервалом (конечным или бесконечным), либо сегментом.
Замечание. Рассмотрение сегмента необходимо для применения неопределенного интеграла в дальнейшем для вычисления определенного интеграла.
Определение. Функция F(x) называется первообразной (функцией) для функции f(x) на множестве М, если она дифференцируема в каждой точке х множества М и
F ′(x) = f(x) x M .
Замечание. В концевых точках сегмента рассматриваются односторонние производные.
Пример. f(x)=2x F(x) = x2 x (−∞,+∞)
Действительно:
F ′(x) = 2x x (−∞,+∞)
Очевидно, что если F(x) является первообразной для функций f(x) на множестве М, то F(x)+C (C = const) также является первообразной для f(x) на множестве М
|
[F(x) + C] |
′ |
|
|
|
= F ′(x) = f(x) . |
|
|
|
|
|
Теорема 1. Пусть F1(x) и F2(x) – любые первообразные для функции f(x) на множе-
стве М, тогда F1(x) – F2(x) = С x M, где С = const.
Доказательство. Положим, G(x)= F1(x) – F2(x), тогда G(x) дифференцируема на М (в случае сегмента в концевых точках существуют односторонние производные) и
G ′(x) = (F (x) − F |
2 |
(x))′ |
= F ′ |
(x) − F |
′ |
(x) = f(x) − f(x) = 0 |
x M , |
1 |
|
1 |
|
2 |
|
|
|
откуда следует, что G(x)=C =const |
x M , т.е. |
|
|
||||
F1(x) – F2(x) ≡ С=const x M .
Теорема доказана. Таким образом показано, что любые первообразные для одной и той же функции на множестве М могут отличаться лишь на константу.
Следствие. Если F(x) – одна из первообразных для f(x) на множестве М, то любая первообразная Φ(х) для f(x) на М представляются в виде Φ(х)=F(x)+C, где С – некоторая константа.
6.2. Неопределенный интеграл
Определение. Совокупность всех первообразных функций функции f(x) на множестве М называется неопределенным интегралом от функции f(x) (на этом множестве) и обозначается символом
∫ f(x)dx .
148

6.НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Вэтом обозначении знак ∫ называется знаком интеграла, выражение f(x)dx – по-
дынтегральным выражением, а функция f(x) – подынтегральной функцией.
Если F(x) – одна из первообразных функций для функции f(x) на множестве М, то в силу следствия из теоремы п.1.1.
∫ f(x)dx = F(x) + C , |
(1) |
где С – любая постоянная. Это равенство следует понимать как равенство двух множеств, точнее следовало бы записать так:
|
∫ f(x)dx = {F(x) + C} . |
|
|
Пример. ∫cosdx = sin x + C |
− ∞ < x < +∞. |
|
|
Замечание. Если F(x) – первообразная функции f(x) на множестве М, то в формуле |
|||
(1) под знаком интеграла |
стоит |
дифференциал функции F(x), |
действительно: |
dF = F ′(x)dx = f(x)dx . |
|
|
|
Будем считать по определению, что |
|
||
∫ f(x)dx ≡ ∫ F ′(x)dx ≡ ∫dF(x) . |
|
(2) |
|
6.3. Основные свойства неопределенного интеграла |
|
||
10. Пусть функция F(x) дифференцируема на М, тогда |
|
||
∫dF(x) = F(x) +c или |
∫ F ′(x)dx = F(x) +c . |
|
|
Справедливость этих равенств вытекает из соотношений (1), (2) п.6.2. |
|||
20. Пусть функция f(x) имеет первообразную на множестве М, тогда |
|
||
d∫ f(x)dx = f(x)dx |
|
|
|
Здесь под интегралом ∫ f(x)dx |
понимается любая первообразная F(x) функции f(x). Спра- |
||
ведливость этой формулы очевидна в силу определения первообразной: так |
|
||
∫ f(x)dx = F(x) +c d∫ f(x)dx = d[F(x) +c] = dF(x) = F ′(x)dx = f(x)dx . |
|||
30. Если функции f1(x) и f2(x) имеют первообразные на М, то и функция |
|
||
f1(x) + f2(x) также имеет первообразную на М, и |
|
||
∫[f1 (x) + f2 (x)]dx = ∫ f1 (x)dx + ∫ f2 (x)dx . |
(1) |
||
Это равенство означает совпадение двух множеств функций, т.е., что сумма какихлибо первообразных для функций f1(x) и f2(x) является первообразной для функции f1(x) + f2(x), и наоборот, всякая первообразная для функции f1(x) + f2(x) является суммой некоторых первообразных для функций f1(x) и f2(x).
Доказательство. Пусть ∫ f1 (x)dx = F1 (x) +c1, ∫ f2 (x)dx = F2 (x) +c2 ;
Положим F(x)=F1(x)+F2(x), тогда F(x) дифференцируема на М и
( |
x |
) |
= |
( 1 ( |
x |
) |
+ F |
2 ( |
x |
)) |
′ |
1 ( |
) |
2 ( |
x |
) |
1 ( |
x |
) |
+ f |
2 |
( |
x |
) |
x M, |
F ′ |
|
F |
|
|
|
= F ′ x |
|
+ F ′ |
|
= f |
|
|
|
|
т.е F(x) является первообразной функции f1(x) + f2(x) на М. Таким образом,
∫(f1 (x) + f2 (x))dx = F(x) +c = F1 (x) + F2 (x) +c,
149

6. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
∫ f1 (x)dx + ∫ f2 (x)dx = F1 (x) +c1 + F2 (x) +c2 = F1 (x) + F2 (x) +c1 +c2
Так как с1+с2 – также произвольная постоянная, то множества
{F1 (x) + F2 (x) +c1 +c2 } и {F1 (x) + F2 (x) +c} совпадают.
Свойство 30 доказано. Аналогично доказывается, что
∫[f1 (x) − f2 (x)]dx = ∫ f1 (x)dx − ∫ f2 (x)dx .
40. Если функция f(x) имеет первообразную на М и а R, то функция аf(x) также имеет на М первообразную, причем при а≠0 имеет место равенство
∫af(x)dx = a ∫ f(x)dx |
(2) |
Доказательство. Пусть ∫ f(x)dx = F(x) +c , тогда (aF(x))′ = aF ′(x) = af(x) . Таким |
|
образом a ∫ f(x)dx = a(F(x) +c) = aF(x) +ac, |
∫af(x)dx = aF(x) +c1. |
Так как а≠0, то ас также является произвольной постоянной, и множества {aF(x) +ac},{aF(x) +c} совпадают. Свойство 40 доказано.
Свойства 30 и 40 выражают свойства линейности неопределенного интеграла относительно подынтегральной функции.
Вопрос о существовании первообразных остается пока открытым.
6.4. Таблица основных неопределенных интегралов
Ранее мы получили таблицу производных основных элементарных функций. Каждая формула таблицы производных простейших элементарных функций, устанавливающая, что та или иная функция F(x) имеет производную f(x), приводит нас, в силу определения неопределенного интеграла, к соответствующей формуле интегрального исчисления
∫ f(x)dx = F(x) +c .
Таким образом, приходим к следующей таблице интегралов.
1. |
∫0 dx = c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. |
∫1 dx = x +c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. |
∫ xαdx = |
|
xα+1 |
|
|
+c |
(α ≠ −1) |
|
|
|
|
|
|
|
||||||||||||
|
α + |
1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
при x > 0 ln |
x |
|
|
|
= ln x и(lnx) |
= |
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||
4. |
∫ |
= ln |
|
x |
|
+c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
при x < 0 ln |
|
x |
|
= ln(− x)и[ln(- x)]′ = − |
1 |
(−1) = |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. ∫a xdx = |
|
a x |
|
|
|
|
(0 < a ≠1), ∫exdx = ex +c |
|
|
|
x |
|
x |
|||||||||||||
|
+c |
|
|
|
|
|
|
|
||||||||||||||||||
|
ln a |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.∫ sin xdx = −cosx +c
7.∫cos xdx = sin x +c
150
