Высшая математика

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

При ∆x→0 все слагаемые правой части, начиная со второго, стремятся к нулю, т.к. содержат ∆x в некоторой положительной степени. Первое слагаемое ∆x не содержит, поэтому предел правой части при ∆x→0 равен nxn-1. Следовательно, существует предел левой части при ∆x→0, равный nxn-1. По определению производной указанный предел равен

производной функции y=xn, т.е. y′ = (xn )′ = nxn −1 .

Данные рассуждения справедливы для любой точки x (-∞, +∞). Кроме того, эту формулу можно обобщить на тот случай, когда n является произвольным вещественным числом (доказательство этого положения см. в п. 4.6.).

3. y=sinx.

2

предел правой части равенства (1) существует и равен cosx (на основании теоремы 1 п.3.10), а тогда и предел левой части этого равенства существует и равен cosx. По определению производной указанный предел равен производной функции y=sinx, т.е.

(sin x)′ = cos x .

4.Аналогичным образом можно показать, что (сosx)′ = −sin x .

5.y = loga x(0 < a ≠1). Пусть x (0,∞), и ∆x – произвольное приращение аргумента, такое

1 См., например: Ильин В.А., Позняк Э.Г. Основы математического анализа.- -М.: Наука, 1971 (и последующие издания), ч.1.

111

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Прежде, чем вычислять производные других элементарных функций, докажем теорему о производной обратной функции.

Теорема.

Пусть функция y=f(x).

1)определена, непрерывна и строго монотонна в некоторой окрестности точки x0.

2)в точке x0 существует отличная от 0 производная f ′(x0 ) ≠ 0. Тогда и обратная функция

tgβ = tg1α.

112

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Используя эту теорему, можно получить производные следующих элементарных функций, являющихся строго монотонными в области их определения.

8. y = a x (0 < a ≠1) Функция y = a x (−∞ < x < +∞) является обратной для логарифмической функции x = loga y , определенной на полупрямой y>0. Поскольку в окрестности любой

(arctgx)′ = 1 +1x2 . 12. По аналогии с предыдущим (arcctgx)′ = −1 +1x2 .

Сведем теперь в единую таблицу производные элементарных функций.

3.(a x )′ = a x ln a(0 < a ≠1). В частности (ex )′ = ex .

4.(sin x)′ = cos x.

113

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

10.(arctgx)′ = 1 +1x2 .

11.(arcctgx)′ = −1 +1x2 .

производные которых вычисляются по следующим формулам:

12.(shx)′ = chx

13.(chx)′ = shx

14.(thx)′ = ch12x

15.(cthx)′ = − sh12x (x≠0).

5.6. Правило дифференцирования сложной функции

Теорема. Пусть

1) задана сложная функция y = f[ϕ(t)], где x=ϕ(t) и y=f(x),

2) функция x=ϕ(t) дифференцируема в точке t0 , а функция y=f(x) дифференцируема в соответствующей точке x0=ϕ(t0). Тогда сложная функция f[ϕ(t)] дифференцируема в точке

t0, причем{f[ϕ(t 0 )]}′ = f ′(x0 )ϕ′(t 0 ).

114

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Пример 2. Найти производную функции

Если А≠0, то слагаемое А∆x есть линейная и однородная относительно ∆x функция.* При

нечно малая более высокого порядка, чем ∆x. Итак, при А≠0 первое слагаемое А∆x является главной частью приращения дифференцируемой функции.

Определение. При А≠0 дифференциалом функции y=f(x) в данной точке x , соответствующим приращению аргумента ∆x, называют главную линейную относительно ∆x часть приращения этой функции в точке x. Символическое обозначение дифференциала функции y = f (x): dy.

Итак, по определению, dy=A∆x или dy = df(x) = f ′(x)∆x (вытекает из теоремы 1

п.4.3.).

Если А=0, то первое слагаемое A∆x равенства (1) перестает быть главной частью приращения дифференцируемой функции, ибо A∆x=0, а α∆x≠0 однако, по договоренности и в этом случае считают

dy= A∆x=0.

* Функция y=Ax+B, где A≠0 -линейная функция аргумента x, где A и B- некоторые постоянные. Если В=0, то линейная функция называется однородной.

115

5.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

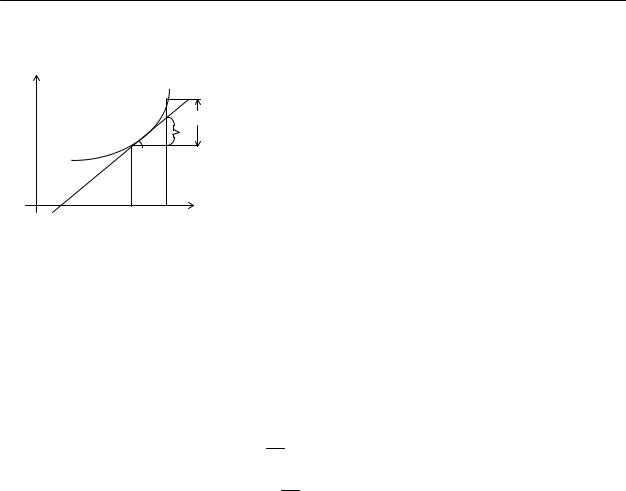
5.8.Геометрический смысл дифференциала функции

5.9. Дифференциал независимой переменной

Под дифференциалом dx независимой переменной x понимают любое, не зависящее от x, число, поэтому, по определению, дифференциалом независимой переменной x называют ее приращение ∆x, т.е. полагают, что dx=∆x.

Введенное определение оправдывается следующими рассуждениями. Рассмотрим независимую переменную x как функцию вида y=x, тогда

dy = dx = f ′(x)∆x =1 ∆x и dx = ∆x .

Таким образом, если аргумент x функции y=f(x) является независимой переменной, то dy = f(x)∆x = f ′(x)dx и f ′(x) = dydx .

Замечание. f ′(x) есть число, а dydx – отношение неопределенных чисел dy и dx,

которые изменяются пропорционально c коэффициентом пропорциональности f ′(x) .

5.10. Инвариантность формы первого дифференциала

В предыдущем пункте было показано, что если x есть независимая переменная функции y=f(x), то dy=f′(x)dx. Покажем, что эта формула справедлива и в том случае, когда аргумент x является дифференцируемой функцией некоторой новой переменной t. Это свойство дифференциала называется инвариантностью его формы.

Итак, пусть дана функция y = f(x) c′(x), и x = ϕ(t) c′(t). Рассмотрим сложную функцию y=f[ϕ(t)]. Если рассматривать здесь t как независимую переменную, то по опре-

переписать в виде dy = f ′(x)ϕ′(t)dt, и из (2) имеем dy = f ′(x)dx.

Итак, в любом случае дифференциал функции y=f(x) может быть записан в форме dy = f ′(x)dx , будет ли x независимой переменной или нет; разница будет в том, что если

за независимую переменную выбрано t, то dx означает не произвольное приращение ∆x, а дифференциал x как функции от t.

116

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

5.11. Производные высших порядков

y′′ = (y′)′ .

Аналогично определяется производная y(n ) любого порядка n=1, 2, ...

Если существует производная y(n −1) (n-1)-го порядка, то по определению y(n ) = [yn −1 ]′.

При этом производная нулевого порядка – сама функция y(0) = y , а производная первого порядка – производная y′ . Символическая запись производной n-го порядка функции y=f(x) на {x}:f(x) c(n ) [{x}].

Определение 2. Функция называется n раз дифференцируемой на {x}, если на {x} она имеет производные до порядка n включительно.

Сформулируем (без доказательства) теорему о вычислении n-ой производной произведения и суммы двух функций, имеющую большое прикладное значение.

Теорема.

Пусть функции y1=f1(x) и y2=f2(x) определены в некоторой окрестности точки x0, имеют производные n-го порядка в точке x0, тогда функции

y1 + y2 = f1 (x) + f2 (x) и y1y2 = f1 (x)f2 (x) также имеют производные n-го порядка в точке

1 Доказательство см.: Ильин В.А., Позняк Э.Г. Основы математического анализа. -М.: Наука, 1971 (и последующие издания) ч.1.

117

5.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

5.12.Дифференциалы высших порядков

Для удобства проведения дальнейших выкладок для обозначения дифференциала

x (x0 − δ, x0 + δ) , тогда

δ(dy) = δ[f ′(x)dx]x =x 0 = [f ′(x)dx]′x =x 0 δx = f ′′(x0 )dxδx = f ′′(x0 )dx2 .

Определение. Значение δ(dy) дифференциала от первого дифференциала dy в некоторой точке x0, взятое при δx=dx, называют вторым дифференциалом функции y=f(x) (в точке x0) и обозначают символом d 2y, т.е . d 2y = f ′′(x0 )dx2 .

Замечание 1. Из определения следует, что d2x=0, т.к. приращение ∆x=dx считается постоянным.

Аналогично определяются дифференциалы более высоких порядков. Предположим, что производная (n-1)-го порядка y(n −1) дифференцируема в окрест-

ности точки x0 (т.е. функция y=f(x) имеет в точке х0 производную n-го порядка), тогда дифференциалом n-го порядка dny функции y=f(x) в точке х0 называется дифференциал

δ(d n −1y) от дифференциала (n-1)-го порядка dn-1y, взятый при δх=dx, т.е.

d n y = δ(d n −1y)δx=dx .

Замечание 2. Формулы (1) и (2) справедливы при n>1 лишь в том случае, когда x является независимой переменной, т.е. второй и последующие дифференциалы не обла-

и мы имеем дополнительный, отличный от 0 член f ′(x)d 2x.

118

5.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

5.13.Дифференцирование функции, заданной параметрически

Функция y = ψ[ϕ−1 (x)]называется заданной параметрически формулами x=ϕ(t) и y=ψ(t) функцией.

Если x=ϕ(t) и y=ψ(t) имеют в точке t0 производные и если ϕ′(t0 ) ≠ 0, ” y = ψ[ϕ-1(t)] имеет

в точке x0=ϕ(t0) производную, причем

y′x = ψ′((t 0 )) (1) ϕ′ t 0

Действительно, по правилу дифференцирования сложной функции и обратной функции имеем:

воспользоваться формулой (1) и правилом дифференцирования частного.

5.14.Свойства дифференцируемых функций

1.5.14.1.Возрастание (убывание) функций в точке. Локальный экстремум.

1.Рассмотрим функцию y=f(x), определенную в некоторой окрестности U(c) точки с.

Определение 1. Функция f(x) называется возрастающей в точке С, если существует δ – окрестность точки c(Uδ(c)) такая, что

x > c f(x) > f(c)

Определение 2. Функция f(x) называется убывающей в точке С, если существует δ

– окрестность точки c(Uδ(c)) такая, что

x > c f(x) < f(c)

119

5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Определение 3. Точка с называется точкой локального максимума (локального минимума) функции f(x) (f(x) имеет локальный минимум в точке С), если существует такая δ – окрестность точки c(Uδ(c)) такая, что

(U δ (c) U(c)) ( x U δ (c) f(x) ≤ f(c)),

(U δ (c) U(c)) ( x U δ (c) f(x) ≥ f(c)).

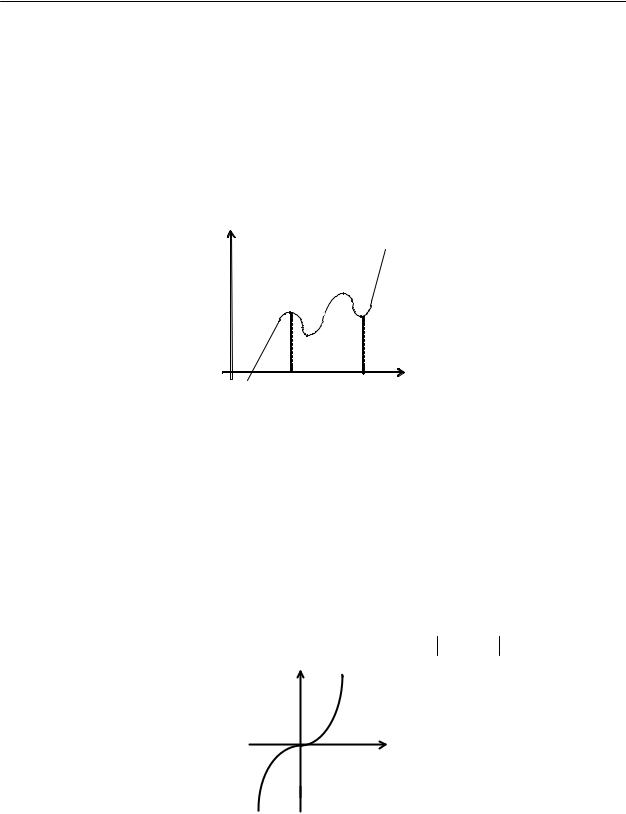
Определение 4. Будем говорить, что функция y=f(x) имеет в точке С локальный экстремум, если эта функция имеет в точке С либо локальный максимум, либо локальный минимум (рис.1)

y

y=f(x)

Рис. 1

Функция f(x) имеет в точке с1 локальный максимум, в точке с2 – локальный минимум. Заметим, что f(с1)<f(с2).

Теорема 1. (лемма Ферма) (достаточное условие возрастания (убывания) функции в точке). Пусть функция f(x) дифференцируема в точке с и f′(c)>0 (f′(c)<0), тогда y=f(x) возрастает (убывает) в точке С.

Замечание 1. Положительность (отрицательность) производной f ′(c) не является

необходимым условием возрастания (убывания) дифференцируемой в точке С функции y=f(x).

Пример 1. (рис.2). f(x)=x3 возрастает в точке х = 0, но y′ x=0 = 3x2 x=0 = 0

y

y=x3

x

Рис. 2

Теорема 2. (необходимое условие экстремума дифференцируемой в данной точке функции) (теорема Ферма).

120