Лабораторные по физике

Выражение для вращательного момента М, приложенного к маятнику, имеет вид

всех действующих на тело внешних сил относительно оси О). Момент инерции J играет при вращательном движении тела такую же

роль, какую масса при поступательном, т.е. является мерой инертности тела при вращательном движении, и характеризует распределение массы по объему тела.

Момент инерции материальной точки относительно оси равен произве-

Для протяженных тел момент инерции определяется как сумма моментов инерции отдельных элементарных масс mi, на которые можно разбить тело, то есть

i=1

где интеграл распространяется на весь объем тела.

Момент инерции математического маятника относительно оси подвеса О, согласно формуле (6.3), равен

С учетом значений (6.1) и (6.5) основной закон динамики (6.2) для маятника приобретает вид

61

получим дифференциальное уравнение колебаний математического маятника

Уравнение (6.8) нельзя проинтегрировать по времени при помощи элементарных функций. Поэтому мы ограничимся рассмотрением малых колебаний маятника, считая sin ϕ ≈ ϕ. Тогда вместо уравнения (6.8) имеем следующее приближенное дифференциальное уравнение малых колебаний маятника:

Общее решение этого уравнения имеет вид

ϕ = А cos(ωot + α),

где А и α – произвольные постоянные, определяемые по начальным условиям движения.

Величина А, то есть наибольшее значение угла отклонения маятника от вертикали, называется амплитудой колебания, ωo − циклической частотой (ω = 2πν, ν − частота колебаний), аргумент (ωot + α) − фазой колебания, а величина α − начальной фазой колебания (значение фазы в начальный момент, то есть при t=0).

Таким образом, при малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону. При больших углах отклонения маятник будет совершать сложное колебательное движение. Как следует из уравнения (6.7) частота ωo при малых колебаниях маятника зависит от его длины и от ускорения свободного падения и не зависит от массы маятника. Период малых колебаний математического маятника, если заменить ωo его значением из уравнения (6.7), определится формулой

62

Период колебаний маятника при малых амплитудах не зависит от амплитуды. Это свойство называется изохронностью колебаний маятника (открыто Г. Галилеем в 1583 г.).

6.2.2Физический маятник

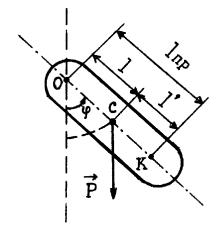
Физическим маятником называется твердое тело, показанное на рисун ке 6.2, которое может вращаться (качаться) вокруг неподвижной оси О под действием собственного веса [1].

Рассмотрим колебания с учетом формы и расположения отдельных элементов массы маятника. На маятник, отклоненный от положения равновесия, действуют внешние силы: сила тяжести Р и реакция оси подвеса О. Трением в оси пренебрегаем. Реакция оси подвеса не имеет момента относительно оси вращения. Момент, стремящийся вернуть маятник в положение равновесия, равен

М = −mgℓ sinϕ,

где m − масса маятника;

ℓ − расстояние между точкой подвеса О и центром масс маятника С.

Рисунок 6.2 − Физический маятник

Дифференциальное уравнение (6.2) вращения тела вокруг неподвижной оси О принимает для маятника вид

где J − момент инерции маятника относительно оси 0.

63

В случае малых колебаний уравнение (6.11) переходит в уже известное нам уравнение (6.9):

В соответствии с выражением (6.13) период колебаний физического маятника определяется выражением

Значит, физический маятник так же, как математический, обладает свойством изохронности, пока отклонения малы.

Из сопоставления равенств (6.10) и (6.14) получается, что математический маятник с длиной

имеет такой же период колебаний, как и данный физический маятник. Таким образом, формула (6.14) для периода колебания физического маятника принимает вид, аналогичный формуле (6.10) для периода колебаний математического маятника:

Величину ℓпр называют приведенной длиной физического маятника.

Приведенная длина физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Так как в выражение момента инерции J входит масса, то приведенная длина физического маятника ℓпр не зависит от его полной массы, а зависит только от его геометрической формы и распределения масс.

Точка К на прямой, соединяющей точку подвеса с центром масс С, лежащая на расстоянии приведенной длины от оси вращения, называется

центром качания физического маятника.

64

По теореме Штейнера [1] момент инерции маятника J относительно оси О может быть представлен в виде

где Jс − момент инерции относительно оси С, параллельной оси вращения О

ипроходящей через центр масс С маятника;

ℓ− расстояние между осями O и С.

Подставив значение J в формулу (6.15), получим

Отсюда следует, что приведенная длина ℓпр всегда больше ℓ, так что точка подвеса и центр качания лежат по разные стороны от центра масс.

Докажем, что при подвешивании маятника в центре качания К приведенная длина, а значит и период колебаний будут теми же, что и вначале. Действительно, возьмем за ось вращения ось К, параллельную оси О (см. рисунок 6.2); тогда для этой оси на основании равенства (6.15)

Подставляя данное выражение в формулу (6.19), получим

Правая часть равенства (6.20) представляет собой приведенную длину ℓпр данного маятника при старой оси подвеса 0 (см. равенство (6.15)), откуда и следует доказываемое:

ℓпр’= ℓпр.

65

Согласно равенству (6.16) будут равны и соответствующие периоды качаний маятника. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

На установленном свойстве взаимности основано определение ускорения свободного падения с помощью так называемого оборотного маятника.

Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов, опорные призмы, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжелые грузы. Если бы с помощью перемещения грузов можно было добиться того, чтобы при подвешивании маятника за любую из призм периоды колебаний были одинаковы, то расстояние между опорными ребрами призм было бы равно ℓпр − приведенной длине маятника. Тогда, измерив период колебаний маятника и зная ℓпр, из формулы (6.16) можно было бы вычислить ускорение свободного падения g. Однако, добиться полного совпадения периодов колебания около обеих осей подвешивания путем последовательного перемещения грузов чрезвычайно трудно. Поэтому поступают следующим образом [2].

При наблюдении колебаний около обеих осей мы получим несколько различные периоды (см. формулу (6.14))

где а1 и а2 − расстояния от центра тяжести до осей качания;

J1 и J2 − моменты инерции маятника относительно соответствующих

осей качания.

Согласно теореме Штейнера

66

Умножая обе части первого уравнения на a1, а второго − на а2 и вычитая одно из другого, будем иметь

Уравнение (6.21) позволяет достаточно просто и с необходимой степенью точности найти величину ускорения свободного падения при приближенном равенстве периодов колебания оборотного маятника.

Отметим, что применение физического маятника как оборотного

позволяет избежать определения момента инерции J, которое даже для тел

самой простейшей формы не может быть произведено с требуемой

точностью.

Величина нормального ускорения свободного падения на уровне моря на 45-м градусе северной широты составляет 9,80655 м/с2. На полюсах

ускорение свободного падения больше (9,832 м/с2), а на экваторе меньше

(9,780 м/с2). Широта г.Томска составляет приблизительно 57 градусов северной широты. Следовательно, полученное из эксперимента значение

должно находиться в интервале от 9,806 до 9,832 м/с2.

6.3Приборы и принадлежности

1.Универсальный маятник на кронштейне.

2.Набор тяжелых шариков.

3.Секундомер.

4.Масштабная линейка.

5.Штангенциркуль.

6.Призма балансировки для нахождения центра тяжести маятника.

7.Гаечный ключ.

6.4Описание конструкции универсального маятника [3]

Универсальный маятник, показанный на рисунке 6.3, представляет

собой настенный кронштейн 1, на котором смонтированы подушки 2 опорных призм и крепление нитей 3 бифилярного подвеса математического маятника. На кронштейне подвешен на опорной призме 4 физический

67

маятник, который при перемене точки подвеса, то есть при подвесе физического маятника на призме 5, превращается в оборотный.

На металлическом стержне маятника между опорными призмами жестко закреплена чечевица 6, а чечевица 7, закрепленная на конце стержня, может перемещаться по шкале 8 с нониусом 9 и закрепляться в нужном положении винтом 10. Расстояние между призмами постоянное и равно 730-740 мм.

Математический маятник выполнен в виде тяжелого шарика 11 диаметром 26 мм, подвешенного бифилярно на нити. Для изменения длины бифилярного подвеса служит барабанчик 12, на который наматывается нить.

6.5 Безопасность труда

В процессе работы необходимо учитывать значительный вес физического (оборотного) маятника. При недостаточно прочном закреплении чечевицы на стержне маятника, при неточной установке маятника в подушки опорной призмы возможны падения маятника или чечевицы.

Устанавливая чечевицу на определенных расстояниях, необходимо тща-

Рисунок 6.3 − Универсальный маятник

тельно закреплять ее на стержне физического (оборотного) маятника винтом 10 (см. рисунок 6.3).

Подвешивая оборотный маятник на опорных призмах, необходимо сле-

дить за точным помещением его в подушки опорных призм.

Определяя центр инерции оборотного маятника, следует соблюдать

осторожность и не допускать скатывания маятника с острия подставки при

уравновешивании маятника.

6.6 Порядок выполнения работы

6.6.1Изучение математического маятника [4]

68

6.6.1.1Установить длину маятника примерно 100-120 см.

6.6.1.2Определить длину маятника. Для этого измерить линейкой

расстояние между осью подвеса и нижним краем шарика, а штангенциркулем диаметр шарика. Вычислить длину маятника как расстояние от оси подвеса до центра тяжести шарика.

6.6.1.3 Отвести маятник от положения равновесия на небольшой угол (~5о), указанный на стенке, и опустить шарик, предоставив ему возможность свободно качаться. В момент наибольшего отклонения маятника пустить в ход секундомер и отсчитать время t, в течение которого маятник совершит N полных колебаний (N = 40 − 60). Измерение времени

N колебаний при неизменной длине ℓ произвести три раза.

6.6.1.4Проделать аналогичные измерения еще для двух разных длин маятника так, чтобы каждая последующая длина была меньше первоначальной примерно в два и в четыре раза.

6.6.1.5Подсчитать периоды колебаний для каждой из трех длин маят-

ника по формуле

где tср − среднее значение времени из трех измерений для каждой длины; N − число полных колебаний.

6.6.1.6 Сверить найденные значения периода со значениями, вычислен-

ными по формуле (6.10). Данные измерений и вычислений занести в табли-

цу 6.1.

Таблица 6.1 − Исследование зависимости периода колебаний маятника от

его длины

Длина маятника 1, м

Число колебаний N

Время колебаний t, с

Среднее время колебаний tср, с

Средний период колебаний Tср, с

Период, вычисленный по формуле (6.10), Tтеор, с

6.6.1.7 Повторить 6.6.1.1 − 6.6.1.3 для трех маятников одинаковой дли-

ны, но отличающихся массой. Использовать для этого шарики, заметно отличающиеся по весу. Масса шариков указана на их поверхности. Результаты измерений записать в таблицу 6.2.

69

6.6.1.8По формуле (6.22) рассчитать периоды колебаний для каждого из

трех маятников, беря за tср среднее значение времени из трех измерений для каждой массы маятника. Результаты вычислений занести в таблицу 6.2.

6.6.1.9Проанализировать полученные в п.п. 6.6.1.1 − 6.6.1.8 результаты.

6.6.1.10Записать вывод.

Таблица 6.2 − Исследование зависимости периода колебаний

1-ый маятник

2-ой маятник

3-ий маятник

6.6.2 Определение ускорения свободного падения методом оборотного маятника

6.6.2.1Снять маятник и укрепить чечевицу 7 с помощью винта 10 на

отметке 6 см основной шкалы, нанесенной на стержне (см. рисунок 6.3).

6.6.2.2Подвесить маятник на призму 4 (нониус вверху) и отклонить его от положения равновесия на небольшой угол (5о − 6о). С помощью секундомера определить время t, за которое маятник совершит N полных колебаний (N = 40-60). Опыт проделать два раза.

6.6.2.3Перевернуть маятник, подвесить его на второй призме 5 (нониус

внизу) и вновь произвести те же измерения.

6.6.2.4Передвигая чечевицу 7 через 1 см в пределах от 6 до 11 см основной шкалы, проделать измерения, описанные в пунктах. 6.6.2.2 − 6.6.2.3, для

каждого из положений чечевицы.

6.6.2.5Подсчитать (с точностью до 0,001 с) периоды колебаний Т1 и Т2 маятника, подвешенного на двух разных опорах, по формуле Т = tср / N, где

tср − среднее значение времени из двух измерений. Результаты измерений и вычислений занести в таблицу 6.3.

6.6.2.6 По данным таблицы 6.3 на миллиметровой бумаге построить графики зависимости Т1 и Т2 от деления шкалы ℓ, на котором находится чечевица.

П р и м е ч а н и е. Графики выполнить на одном рисунке. При построении графиков начало отсчетов вдоль осей координат ℓ и Т, а также

70