16-19
.doc|
16,17.Цепи Маркова. Дискретный
или непрерывный случайный процесс
X(t)
называется Марковским, если для любого
набора
т.е.
если для Дискретный Марковский процесс с дискретным временем называют цепью Маркова. Цепь Маркова имеет вид:
Марковские цепи есть модель схемы независимых испытаний, когда существует зависимость исхода любого состояния только от исхода предыдущего. Имеем
систему с дискретными состояниями.
Если система в момент времени
Следовательно, цепь Маркова определяется через условные вероятности того, что система осуществит длинный переход. Цепь Маркова называется однородной, если переходные вероятности не зависят от времени, т.е.
Обозначим
Матрица квадратная, неотрицательная, ∑ вероятностей по любой строке =1. Многошаговые переходные вероятности. Необходимо
определить вероятность перехода
системы из состояния
|
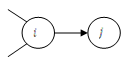
18, Классификация состояний Смежные состояния – возможен переход за один шаг. Граф состояния системы:
Вершины
графа на рисунке – это состояния (все
– вершины на шаге Для построения графа Марковской цепи удобно использовать матрицу смежности.
Состояние
Пользуясь
графовым представлением Марковского
процесса, легко определить множества
состояний, достижимых из фиксированного
состояния Состояния
Все существующие состояния цепи естественно разбиваются на классы так, что все состояния принадлежащие одному классу, сообщаются, а разным классам – не сообщаются. Цепь Маркова называется неприводимой, если существует (ей соответствует) единственный класс сообщающихся состояний. Подмножество С состояний цепи Маркова называют замкнутым если никакое состояние вне С не может быть достигнуто ни из какого состояния, входящего в С.
Отражающий экран:
Поглощающий экран:
|
19. Стационарное состояние цепи Маркова. Эргодические цепи Маркова.
При
Распределение
Алгоритм
нахождений
Цепь Маркова называется однородной, если переходные вероятности не зависят от времени, т.е.
Обозначим
Матрица квадратная, неотрицательная, ∑ вероятностей по любой строке =1.
состояние
Оказывается,
что для нахождения
Вводим промежуточный
момент (шаг)
за
Тогда из формулы полной вероятности:
Следовательно
элемент матрицы, полученный как
произведение
Т.
матрица переходных вероятностей за
Пусть
Если и т.д. т.е.:
Если представить исходное распределение вероятностей состояний системы в виде матрицы-строки:
то
вероятности состояний системы в момент
времени
Можно получить из уравнения:
Марковские модели содержат полную информацию о двумерном законе распределения. Пример Марковского процесса:
Марковский процесс 2-го порядка:
Т.е.
от прошлого |