1.3. Статистическая совокупность

Будем обозначать признаки объектов заглавными буквами X ,Yи т.д. Каждому количественному признаку можно поставить в соответствие его величину. Величины признаков будем обозначать теми же буквами (X,Y, ..), что и сами признаки. Имеющийся к настоящему времени уровень развития измерительной техники таков, что величина любого признака любого биологического объекта может быть с той или иной точностью измерена и выражена числом. Даже качественные признаки можно выражать числом. Например, если признак присутствует, можно поставить ему в соответствие число 1, а если отсутствует – число 0.

Величины признаков делят на дискретные и непрерывные.

Дискретнойназывают (на "практическом" уровне строгости) величину, которая принимает отдельные, изолированные возможные значения. ЕслиX - дискретная величина, то каждое её возможное значение отделено от ближайших других возможных значений "пустыми" промежутками, в которых нет значенийX. Частным случаем дискретных величин являютсяцелочисленные величины, возможные значения которых – целые числа (например, число зерен в колосе, число цветков в соцветии).

Непрерывнойназывают величину, которая может принимать любое значение из некоторого конечного или бесконечного промежутка. Примерами непрерывных величин являются масса, длина, время жизни объекта и т.п.

Измеренное (численное) значение величины признака объекта называют варианта.

Если измерена величина признака X у объекта с номером i из выборочной или генеральной совокупности, то соответствующую варианту обозначаютx_i. Результатом измерения величиныXкаждого объекта выборочной совокупности объемаn является множество вариант:x₁, x₂, x₃, …, x_n. Числа этого множества не упорядочены по величине, некоторые из них могут совпадать. Таким, как правило, является первичный массив экспериментальных данных, получаемый в процессе измерений. Такой первичный неупорядоченный массив экспериментальных данных будем называтьстатистической совокупностью. Статистическую совокупность можно, для краткости, также называть выборкой.

Пример 1.1. Рассмотрим пример статистической совокупности. В результате измерения (на высоте 1,3 м от уровня почвы) диаметровx_i стволов сосен в выборке объемомn = 20 (выборка получена на пробной площади Томского стационара Института леса СО РАН, сосняк осоково-папоротниково-вейниковый, возраст деревьев от 52 до 132 лет) получена следующая статистическая совокупность:

x₁ = 28 смx₂ = 26 смx₃ = 30 смx₄ = 28 смx₅ = 28 см x₆ = 28 см x₇ = 26 см

x₈ = 29 смx₉ = 27 смx₁₀ = 36 смx₁₁ = 29 смx₁₂ = 32 см x₁₃ = 34 см x₁₄ = 30 см

x₁₅ = 38 смx₁₆ = 28 смx₁₇ = 28 смx₁₈ = 23 смx₁₉ = 24 см x₂₀ = 33 см.

Эту (и любую другую) статистическую совокупность можно записать более компактно, например, в виде:

диаметры x_i (в см) стволов сосен

28, 26, 30, 28, 28, 28, 26, 29, 27, 36, 29, 32, 34, 30, 38, 28, 28, 23, 24, 33 .

1.4. Статистические распределения

Пусть изучаемый признак Xявляется дискретным. Пусть из генеральной совокупности извлечена выборка объемаn и произведено измерение признакаX у каждого объекта выборки, причем значениеx₁ наблюдалосьn₁ раз,x₂ - n₂ раз, последнее значение

x_k- n_k раз (очевидно, что ). Если вариантыx_i записаны в возрастающем (по

значениям x) порядке, то такую последовательность вариант называютвариационным рядом. Индексi здесь означает номер варианты в вариационном ряде. Числаn_i появления значенийx_i называютчастотами значений x_i , а их отношения к объему выборки-относительными частотами.

Выборочным статистическим распределением частот называют перечень вариантx_i и соответствующих им частотn_i .Выборочным статистическим распределением относительных частот называют перечень вариантx_i и соответствующих им относительных частотω_i .

Сумма всех относительных частот должна быть равна единице. Действительно

=1.

Если относительные частоты выражены десятичными дробями, томожет быть близка, но не точно равна единице. Это является следствием ошибок округления.

Перечень вариант x_i и соответствующих им частотN_i (относительных частотW_i=) значений признакаX в генеральной совокупности объемаN называютгенеральным статистическим распределением частот (относительных частот). Для многих генеральных совокупностей получение статистического распределения с помощью прямых измерений признака у всех объектов совокупности и подсчетаN_i невозможно, так как числоN объектов генеральной совокупности, как правило, очень велико.

Пример 1.2. Для определения приживаемости саженцев сосны в лесопосадке составлена выборка изn = 60 наборов по 10 саженцев. Таким образом, объектами выборки являются наборы по 10 случайно отобранных саженцев. Подсчитывалось числоx_iвыживших саженцев в каждой десятке. Результаты подсчета приведены в таблице:

8 7 7 10 4 7 9 8 8 9 5 8 9 8 10

9 6 8 8 10 5 8 6 10 9 10 9 7 9 5

4 9 8 7 8 8 9 9 7 8 9 7 8 9 9

10 9 6 8 9 9 7 8 9 7 8 8 6 8 5 .

Составить выборочные распределения частот и относительных частот.

Решение. Записывая вариантыx_i в порядке возрастания, получаем вариационный ряд:

x_i 4, 5, 6, 7, 8, 9, 10,

где x₁ = 4,x₂ = 5,x₃ = 6, …,x₇= 10.

Подсчитывая частоты n_i появления вариантx_i , получаем выборочное распределение частот:

x_i 4 5 6 7 8 9 10

n_i 2 4 4 9 18 17 6 ,

где n₁ = 2 ,n₂ = 4 ,n₃ = 4 , …,n₇ = 6 .

Сумма всех частот n_iравна объему выборкиn ().

Находим относительные частоты :0,033; ==0,067; 0,067;

; =0,3; =0,283; =0,1 .

Составляем выборочное распределение относительных частот:

x_i 4 5 6 7 8 9 10

0,033 0,067 0,067 0,15 0,3 0,283 0,1 .

Контроль вычисления :

0,033 + 0,067 + 0,067 + 0,15 + 0,3 + 0,283 + 0,1 = 1 . Е

Если изучаемый признак является непрерывным или признак является дискретным и число его возможных значений велико, то следует проводить группировку результатов измерений. Группировка проводится в несколько шагов.

1. Среди измеренных значений x_i признака выбирают наименьшее и наибольшее. Затем определяют размах распределения ∆x =x_max–x_min .

2. Определяют число k классов группировки. Как показывает опыт, наиболее целесообразно задаватьkв пределах от 6 - 8 до 15 (k = 6 для небольшого числа данных). Для определенияk можно использовать эмпирическую формулуk = 1 + 4lgn . Например, при

n = 50,lgn = 1,7 иk = 7,8 ≈ 8 ; приn = 100,lgn = 2,0 иk = 9 ; приn = 1000,lgn = 3,0 и

k = 13 .

3. Определяют ширину d интервалов группировки (интервалов разбиения), деля размах распределения на число классов группировки:d = ∆x / k .

4. Определяют границы интервалов разбиения. Границы первого интервала следует выбрать так, чтобы он содержал наименьшее значение изучаемой величины x_min. Последующие интервалы получают, добавляяd к правой границе предшествующего интервала (важно, чтобы частотыn₁ иn_k попадания значенийx_i в первый и последний интервалы разбиения различались не слишком сильно).

5. Значения x_i "разносят" по интервалам разбиения и подсчитывают числаn₁ ,n₂ , …,n_k попадания значенийx_i в первый, второй, …,k – ый интервал разбиения. Числаn₁ ,n₂ , …,n_k называютчастотамипопадания значенийx_i в первый, второй, …,k – ый интервал разбиения. Если два равных друг другу значенияx_iиx_j попадают на границу между интервалами, то одно из них относят к левому, а другое к правому интервалу. Все значения признака, попавшие вi – й интервал разбиения, в некоторых задачах удобно заменить на- координату серединыi – го интервала.

6. Составляют выборочное статистическое распределение частот или относительных частот непрерывного признака в виде перечня интервалов I_i (или координатсередин интервалов) разбиения и соответствующих им частотn_i или относительных частотω_i .

Аналогично (в тех случаях, когда это возможно) может производиться систематизация результатов измерений признака в генеральных совокупностях.

Пример 1.3.Результатыx_i измерений высоты шестидесяти пяти случайно отобранных деревьев (сосны, возраст 48 – 52 года, Богучанский лесхоз) перечислены ниже. Все значенияx_i даны в метрах:

16, 18, 20, 12, 15, 15, 17, 18, 16, 15, 16, 18, 16, 14, 16, 19,

13, 9, 16, 19, 14, 16, 19, 7, 10, 15, 21, 13, 17, 18, 19, 15,

15, 18, 22, 16, 15, 13, 11, 15, 8, 14, 23, 17, 12, 10, 14, 12,

11, 13, 14, 18, 13, 18, 12, 22, 13, 14, 21, 17, 20, 18, 12, 19, 20.

Составить выборочные распределения частот и относительных частот.

Решение. Наименьшее значение высоты дерева x_min = 7 м, а наибольшее значение x_max = 23 м. Объем выборки n = 65; так как 1 + 4 lg 65 ≈ 8,25 , то число интервалов разбиения k можно взять равным 9. Интервалы разбиения указаны в следующей ниже таблице. Границы интервалов разбиения взяты полуцелыми, чтобы не было попаданий x_i на границы. Подсчитывая частоты n_i появления значений x_i , получаем выборочное распределение частот:

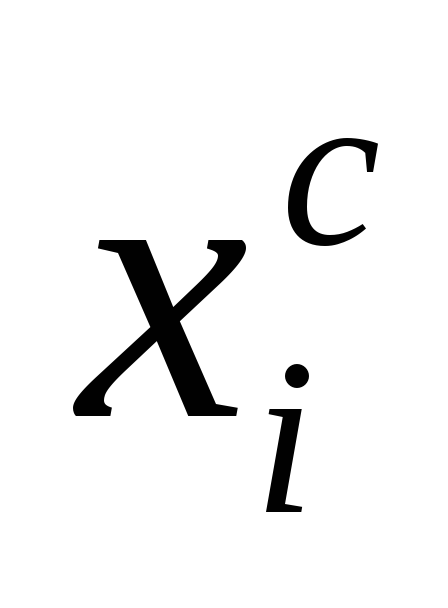
Интервал разбиения		Частоты ni
(6,5; 8,5)	7,5	2
(8,5; 10,5)	9,5	3
(10,5; 12,5)	11,5	7
(12,5; 14,5)	13,5	12
(14,5; 16,5)	15,5	16
(16,5; 18,5)	17,5	12
(18,5; 20,5)	19,5	8
(20,5; 22,5)	21,5	4
(22,5; 24,5)	23,5	1

Находя относительные частоты ,и т.д. , получаем выборочное распределение относительных частот:

Интервал разбиения		Относительные частоты
(6,5; 8,5)	7,5	0,031
(8,5; 10,5)	9,5	0,046
(10,5; 12,5)	11,5	0,108
(12,5; 14,5)	13,5	0,185
(14,5; 16,5)	15,5	0,246
(16,5; 18,5)	17,5	0,185
(18,5; 20,5)	19,5	0,123
(20,5; 22,5)	21,5	0,061
(22,5; 24,5)	23,5	0,015

Контроль: 0,031 + 0,046 + 0,108 + … + 0,061 + 0,015 = 1 . Е

При измерении и систематизации значений признаков в генеральных совокупностях Р типа (например, при изучении множества клеток ткани, множества гидробионтов отдельного водоема и т.д.) следует понимать, что получаемые при этом статистические распределения имеют частный характер, отражая индивидуальную историю формирования совокупности в определенных частных условиях.

Пример 1. 4. В таблице приведены значения ширины древесных колец лиственницы, сформированных за годы, указанные в левом столбце таблицы (район произрастания дерева - бассейн реки Индигирки):

годы ширина x_iкольца (в мм)

1860 0,93 0,78 0,47 0,49 0,56 0,87 1,03 1,02 0,84 0,61

1870 0,98 0,71 0,77 0,98 0,86 0,53 0,69 0,93 0,87 0,60

1880 0,78 1,00 0,59 1,02 0,47 0,61 0,56 0,56 0,84 0,64

1890 0,82 0,60 0,55 0,58 0,73 0,79 0,97 0,73 0,96 0,54

1900 0,68 1,07 1,14 0,77 0,79 0,67 0,80 1,11 0,83 0,55

1910 0,48 0,86 0,93 0,51 0,76 0,48 0,58 0,89 0,43 0,50

1920 0,44 0,47 0,62 0,70 0,66 0,57 0,55 0,37 0,26 0,30

1930 0,54 0,50 0,54 0,60 0,55 0,61 0,49 0,30 0,63 0,60

1940 0,81 0,59 0,92 0,92 0,68 0,34 0,46 0,67 0,80 0,61

1950 0,58 0,52 0,59 0,46 0,37 0,34 0,46 0,33 0,49 0,27

1960 0,53 0,48 0,33 0,29 0,33 0,42 0,29 0,30 0,28 0,42

1970 0,49 0,32 0,19 0,38 0,43 0,34 0,29 0,41 0,24 0,14

1980 0,27 0,23 0,34 0,20 0,11 0,27 0,27 0,21 0,20 0,31

1990 0,23 0,20 0,09 0,08 0,20 0,19 0,19 0,21 0,27.

В каждой строке таблицы (кроме последней) приведены ширины колец за десять последовательных лет развития дерева. Требуется составить выборочное распределение частот и выборочное распределение относительных частот.

Решение. Наименьшее значение ширины кольцаx_min = 0,08 мм, а наибольшее значениеx_max = 1,14 мм. Объем выборкиn = 139; так как 1 + 4lg139 ≈ 9,6 , то число интервалов разбиенияk можно взять равным 10, но удобнее взятьk = 11. Интервалы разбиения указаны в следующей ниже таблице. При подсчете частотn_i оказывается, что имеется четыре варианты (равные 0,55), попадающие на границу между интервалами; две из них относим к левому интервалу, а две к правому.

Выборочное распределение частот имеет вид:

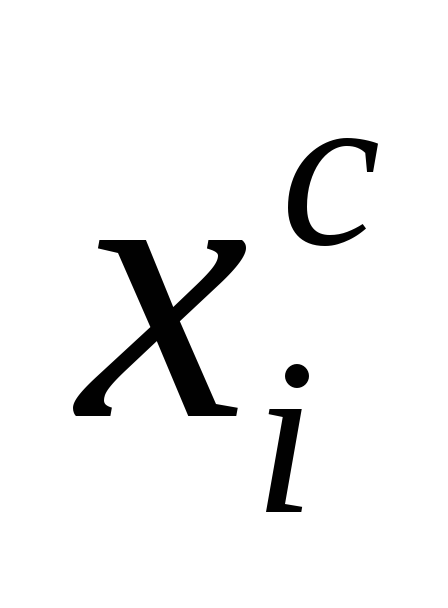
Интервал разбиения		Частоты ni
(0,05; 0,15)	0,1	4
(0,15; 0,25)	0,2	12
(0,25; 0,35)	0,3	22
(0,35; 0,45)	0,4	9
(0,45; 0,55)	0,5	24
(0,55; 0,65)	0,6	23
(0,65; 0,75)	0,7	10
(0,75; 0,85)	0,8	14
(0,85; 0,95)	0,9	10
(0,95; 1,05)	1,0	8
(1,05; 1,15)	1,1	3

Находя относительные частоты, получаем выборочное распределение относительных частот:

Интервал разбиения		Относительные частоты
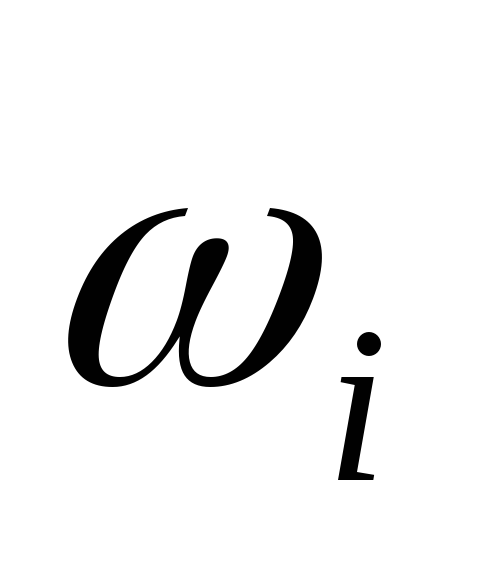
(0,05; 0,15)	0,1	0,029
(0,15; 0,25)	0,2	0,086
(0,25; 0,35)	0,3	0,158
(0,35; 0,45)	0,4	0,065
(0,45; 0,55)	0,5	0,173
(0,55; 0,65)	0,6	0,164
(0,65; 0,75)	0,7	0,072
(0,75; 0,85)	0,8	0,101
(0,85; 0,95)	0,9	0,072
(0,95; 1,05)	1,0	0,058
(1,05; 1,15)	1,1	0,022

Биологические механизмы (деления и роста клеток), определяющие формирование древесного кольца, меняются с возрастом дерева. Если бы климатические условия в каждом году жизни дерева были совершенно одинаковыми, ширина колец, соответствующих разным возрастным периодам дерева, была бы, тем не менее, разной: ширина колец, соответствующих ранним периодам жизни дерева, в среднем больше, чем колец, соответствующих поздним периодам. Кроме того, на ширину кольца влияют (и существенно!) климатические условия: благоприятным климатическим условиям соответствуют относительно более широкие кольца. Полученные в этом примере статистические распределения являются результатом взаимодействия внутренних (биологических) и внешних (климатических) факторов и отражают индивидуальную историю развития только данного дерева. Возможно, что малое (по сравнению с соседними) значение n_i , соответствующее интервалу (0,35; 0,45), характерно только для данного дерева, и не характерно для других деревьев данной местности. Поэтому, например, для определения климатических характеристик прошлых лет по параметрам древесных колец необходимо измерение параметров колец не одного, а достаточно большого числа деревьев.