3. Практическая часть

Для моделирования антилогарифматора и логарифматора с помощью программы Workbench5.0 необходимо нарисовать схему, приведенную на рис. 3

На операционном усилителе DA1 собрана схема антилогарифматора, а наDA2 – логарифматора.

Рис. 3

Для исследования логарифмических и антилогарифмических характеристик преобразователей используется моделирование с вариацией параметров⁴.

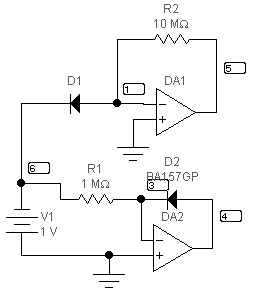
Нужно получить зависимость выходного напряжения антилогарифматора от линейно изменяющегося входного напряжения.

Для этого нужно выбрать пункт меню Analysis/ Parameter Sweep. Появится диалоговое окно моделирования с изменением параметров. В полях указать следующие значения:

Component	V1
Parameter	Voltage
Start Value	0
End Value	0.88 V
Sweep Type	Linear
Increment Size	0.01 V
Output node	Выход DA1

В поле Sweep for: указать DC Operation point.

После заполнения полей нажать кнопку Simulate. В результате моделирования получается зависимость выходного напряжения антилогарифматора от линейно изменяющегося входного напряжения.

Скопировать полученную зависимость и вставить в отчет.

Аналогичным образом исследовать изменение напряжения на выходе логарифматораот линейно изменяющегося входного напряженияпри следующих условиях моделирования:

Component	V1
Parameter	Voltage
Start Value	0
End Value	13 V
Sweep Type	Linear
Increment Size	0.1 V
Output node	Выход DA2

Скопировать полученную зависимость и вставить в отчет.

Контрольные вопросы по заданию 3

1. Что такое функциональное преобразование сигналов?

2. Перечислить основные методы создания нелинейных измерительных преобразователей.

3. Чем отличается функциональное преобразование сигнала от его масштабного преобразования?

4. Какой элемент (или элементы) схемы обеспечивает(ют) реализацию логарифмической и антилогарифмической зависимостей?

Задание 4

1. Цель и задачи задания

1. Изучить метод проведения спектрального анализа сигналов методом разложения в ряд Фурье.

2. Получить практические навыки разложения простейших периодических функций в спектр с помощью программы Workbench5.0.

2. Теоретическая часть

В инженерной практике необходимо уметь «проводить» сложные детерминированные и квазидетерминированные сигналы через различные звенья измерительных устройств, а также генерировать такие сигналы. Эти задачи обычно решаются проще, если сложный сигнал можно представить в виде суммы элементарных.

Разложение сложного сигнала на элементарные, производится по определенной системе, в частности по системе ортогональных функций – в обобщенный ряд Фурье

, (1)

где ‑коэффициенты членов ряда; (t) ‑совокупность ортогональных функций.

Ортогональнойназывается совокупность функцийС_k(t), удовлетворяющая следующему условию на отрезке времени (t₂-t₁):

,

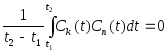где k=1, 2, 3, ...,m; n=1, 2, 3, ...,mприnк.

Ортогональность двух функций означает, что данная функция не содержит в своем составе компонент, имеющих форму второй, ортогональной ей функции.

Если совокупность функций С_k(t)удовлетворяет также и условию

,

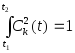то она называется ортонормированной.

Если два вышеприведенных условия ортонормированности функций С_k(t)выполняются, то получаем

.

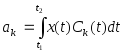Если второе условие не выполнено и совокупность функций является только ортогональной, но не ортонормированной, то

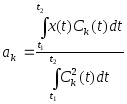. (2)

Следовательно, сложный детерминированный сигналх(t)на интервале(t₂-t₁)можно заменить суммойтвзаимно ортогональных на этом интервале сигналовС_k(t).Погрешность такой аппроксимации будут зависеть от числа членов рядаmи сходимости ряда.

В качестве ортогональных функций используются либо элементарные функции, например тригонометрические, либо специальные функции.

Наиболее часто в качестве ортогональных функций используются тригонометрические функции, образующие обычный ряд Фурье. Ортогональными на любом интервале являются функцииsin(n₀t) иsin(m₀t),sin(п₀t) иcos(m₀t),cos(n₀t) иcos(т₀t), которые обычно называютгармоническимифункциями. В этом случае любой периодический сигналх(t)можно представить на интервале (t_o,t_o+2/₀) рядом (суммой) элементарных сигналов:

,

при t₀<t<t₀+Т.

Коэффициенты a_i ряда Фурье определяются по формулам:

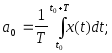
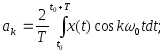
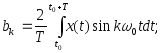
Тригонометрический ряд Фурье применяют также в следующей форме:

,

где

,

.

Аналогично можно показать, что комплексные экспоненциальные функции (k=0, ±1, ±2, ...) также являются взаимно ортогональными на интервале(t_o, t_o+2/₀) при любомt_o.

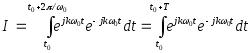
Если k=п,тоI=Т,а прикп I=0.

Следовательно, любой периодический сигнал х(t)можно представить суммой комплексных экспоненциальных сигналов ‑ с помощью экспоненциального ряда Фурье

Коэффициенты экспоненциального ряда Фурье определяются по формуле

Экспоненциальный ряд Фурье для периодической функции является второй формой тригонометрического ряда Фурье.

Периодический сигнал с периодом повторения T можно представить состоящим из периодических синусоидальных сигналов с частотными составляющими _=2/Т; 2_; З_; ...; n_. Периодический сигнал х(t) обладает дискретным или линейчатым спектром, графически изображающимся в виде вертикальных линий вдоль оси частот в точках _, 2_ и т.д. причем высота каждой из этих линий пропорциональна амплитуде данной частотной составляющей (гармоники).

Обычно частотные составляющие спектра являются комплексными числами, и поэтому для представления данной периодической функции необходимо иметь два дискретных спектра: спектр амплитудиспектр фаз(рис. 1). Однако во многих случаях частотные составляющие являются только действительными или только мнимыми, и тогда сигнал можно представить одним спектром, так как его фазовый спектр постоянен и имеет составляющие, соответственно равные 0 или 90°.

Рис. 1 Спектр амплитуд (а) и спектр фаз (б) периодического сигнала

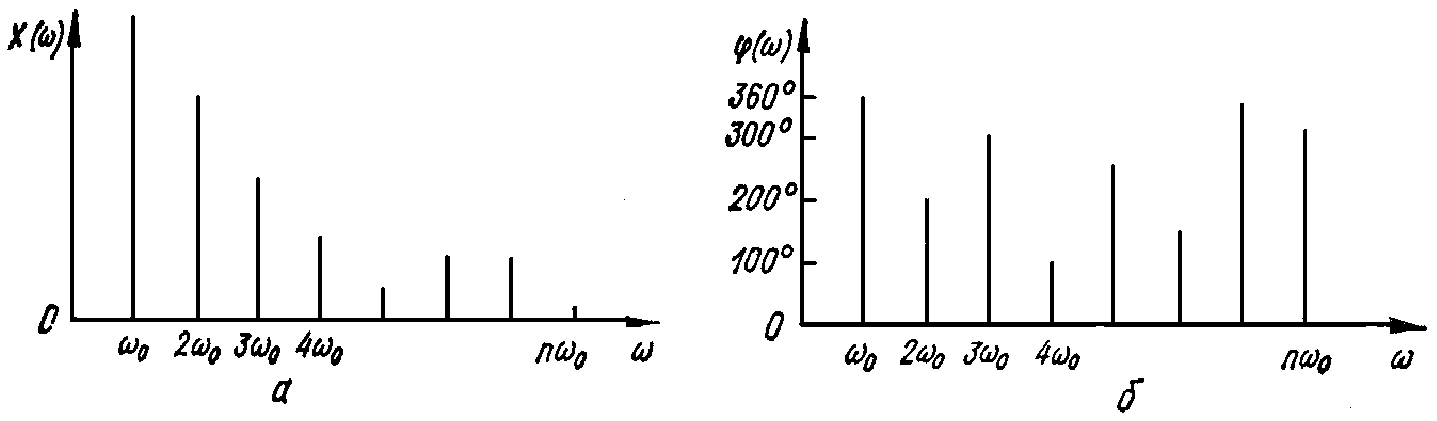
Дискретный спектр периодического сигнала, определяемый с помощью средств измерений, называемых анализаторами гармоник, характеризуется совокупностью важных информативных параметров сигналах(t)‑значениями амплитуд и фаз отдельных гармоник, полосой частот и др.

Под нелинейными искажениями (НИ) понимается любое изменение сигнала, вызывающее искажения передаваемого сообщения и обусловленное нелинейностью тракта. Количественная оценка НИ может быть произведена различными методами: гармоническими, комбинационными, статистическими. Наибольшее применение получили измерители нелинейных искажений, предназначенные для измерения степени искажения формы кривой, т. е. отличия формы сигнала от гармонической. Количественно искажения оценивают двумя коэффициентами: коэффициентом гармоник K_Г и коэффициентом нелинейных искажений K_НИ.

На практике коэффициент гармоник рассчитывается по формуле

,

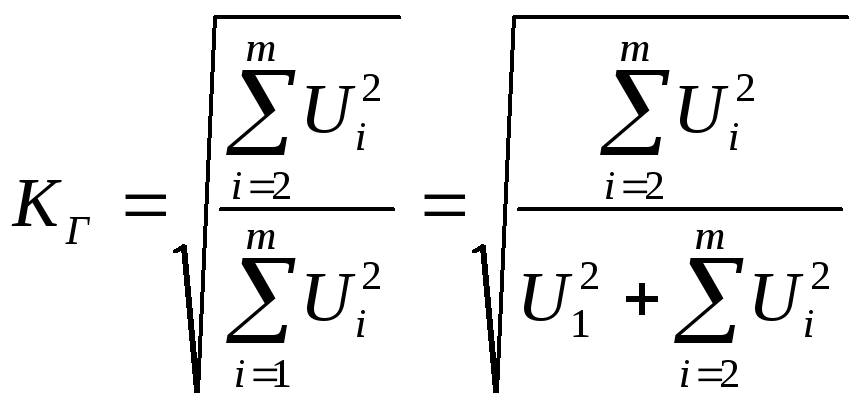где U_i – амплитуда i-й гармоники выходного сигнала.

Из этой формулы видно, что значение коэффициента К_Г может изменяться в пределах от 0 до 1.

Коэффициент нелинейных искажений рассчитывается по формуле

,

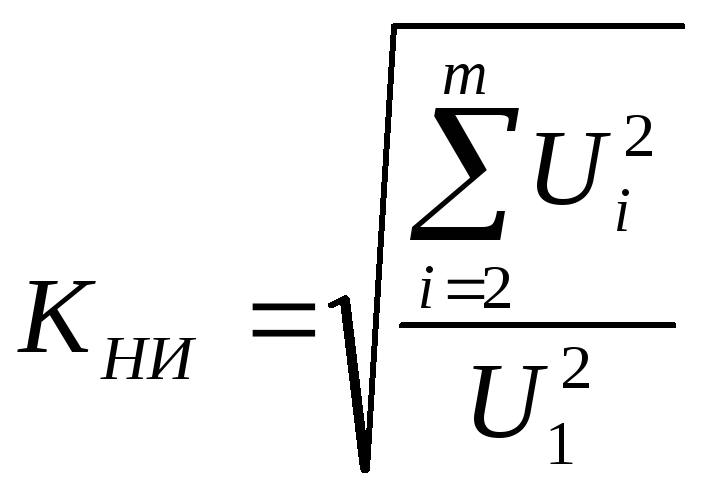где U₁ – амплитуда первой гармоники.

Как правило, измерители нелинейных искажений определяют коэффициент гармоник, а коэффициент нелинейных искажений рассчитывают по простой формуле

.

Видно, что значение коэффициента К_НИ может изменяться от 0 до ∞.

При малых К_НИ можно считать, что К_НИ≈К_Г (в диапазоне К_НИ≤0,1 значения К_Г и К_НИ отличаются менее чем на 1%.