
- •1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- •1.1. Предмет теории вероятностей
- •1.2. Основные понятия теории вероятностей
- •1.3. Классическое определение вероятности
- •1.8. Противоположные события
- •1.11. Условная вероятность
- •Замечание. Справедливо равенство
- •Искомая вероятность
- •Искомая вероятность
- •1.16. Формула полной вероятности
- •1.17. Вероятность гипотез. Формулы Байеса
- •Отсюда
- •1.19. Локальная теорема Лапласа
- •1.20. Интегральная теорема Лапласа
- •1.21. Распределение Пуассона
- •Пример 1.32. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 120 тыс. ден. ед., а число продаж X автомашин в течение дня подчиняется закону распределения
- •Искомая характеристика М(П) находится с использованием указанных ранее свойств математического ожидания:
- •Искомая дисперсия
- •Пример 1.35. Найти дисперсию ежедневной продажи числа автомашин по данным примера 1.31.
- •Решение. Закон распределения случайной величины X2 имеет вид
- •Математическое ожидание М (X2) подсчитывается из этой таблицы:
- •Математическое ожидание М (X)=2,675. Используя формулу (1.7), получаем искомую дисперсию
- •Рассмотрим свойства функции распределения.
- •Решение. Искомая вероятность
- •Итак, искомая функция распределения
- •Свойства плотности распределения.
- •Вопросы для самопроверки
Вопросы для самопроверки
1.Дайте классическое определение вероятности. В чем состоит различие между вероятностью и относительной частотой?
2.Дайте определение условной вероятности. Какие события называют независимыми?
3.Дайте определение произведения событий.
4.Запишите формулу полной вероятности, формулу Бейеса, формулу Бернулли. Сформулируйте локальную теорему Лапласа, интегральную теорему Лапласа, теорему Пуассона. Когда применяются эти теоремы?
5.Дайте определение случайной величины. Приведите примеры.
6.Дайте определение функции распределения случайной величины. Каковы ее свойства?
7.Дайте определение плотности распределения вероятностей. Каковы ее свойства?
8.Как найти вероятность попадания случайной величины в заданный интервал, если она распределена по нормальному закону?
9.Дайте определение математического ожидания случайной величины. Каковы его свойства?
10.Дайте определение дисперсии случайной величины. Каковы ее свойства?
11.Дайте определение среднего квадратического отклонения случайной величины и укажите его преимущества по сравнению с дисперсией.
55
Задачи для самостоятельного решения
1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
Ответ. р = 0,1.
2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.
Ответ. р = 0,5.
3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.
Ответ. р = 0,81.
4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».
Ответ. р = 1/120.
5. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?
Ответ. р = 0,05.
6. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?
Ответ. р = 0,02.
56
7. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.
Ответ. р = 0,4.
8. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.
Ответ. р = 44/45.
9. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной нестандартной детали.
Ответ. р = 2/3.
10. Вероятность того, что стрелок при одном выстреле попадает в мишень, равна р = 0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание.
Ответ. 0,729.
11. Брошены монета и игральная кость. Найти вероятность совмещения событий: «появился «орел»», «появилось 6 очков».
Ответ. 1/12.
12. В двух ящиках находятся детали: в первом—10 (из
57
них 3 стандартных), во втором—15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.
Ответ. 0,12.
13. В студии телевидения 3 телевизионных камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна р = 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера (событие А).
Ответ. 0,936.
14. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей (событие А)?
Ответ. 91/216.
15. Предприятие изготовляет 95% изделий стандартных, причем из них 86% — первого сорта. Найти вероятность того, что взятое наудачу изделие, изготовленное на этом предприятии, окажется первого сорта.
Ответ. 0,817.
16. Вероятность того, что событие А появится хотя бы один раз при двух независимых испытаниях, равна 0,75. Найти вероятность появления события в одном испытании (предполагается, что вероятность появления события в обоих испытаниях одна и та же).
Ответ. 0,5.
58
17. Вероятность поражения цели первым стрелком при одном выстреле равна 0,8, а вторым стрелком — 0,6. Найти вероятность ого, что цель будет поражена только одним стрелком.
Ответ. 0,44.
18. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7, а вторым - 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень.
Ответ. 0,88.
19. У сборщика имеется 16 деталей, изготовленных заводом № 1, 4 детали завода № 2. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной заводом № 1.
Ответ. 92/95.
20. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника — 0,9, для велосипедиста — 0,8 и для бегуна — 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Ответ. 0,86.
21. Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 — 0,9. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
Ответ. 0,84.
59
22. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором — 30 деталей, из них 24 стандартных; в третьем 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика - стандартная.
Ответ. 43/60.
23. В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.
Ответ. 0,625.
24. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй - 6, из третьей группы - 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Ответ. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59,
20/59.
25.В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы;
в) выключены все моторы.
Ответ. а) Р6(4) = 0,246; б) Р6(6) = 0.26; в) Р6(0) = 0,000064.
60
26. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна
0,3.
Ответ. Р= 0,472.
27. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза.
Ответ. Р=1 - [Р8(0) + Р8 (1)] = 0,19.
28. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз.
Ответ. а) Р=7/64; б) Р=57/64.
29. Найти приближенно вероятность того, что при 400 испытания событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.
Ответ. Р400(104) =0,0006.
30. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз.
Ответ. а) Р100(70,80) = 2Ф(1,15) = 0,7498; б) Р100(0; 70)=-Ф(1,15) + 0,5 = 0,1251.
61
31. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
X |
6 |
3 |
1 |
р |
0,2 |
0,3 |
0,5 |
Ответ. 2,6.
32. Производится 4 выстрела с вероятностью попадания в цель р1 = 0,6, р2 = 0,4, р3 = 0,5 и р4 = 0,7. Найти математическое ожидание общего числа попаданий.
Ответ. 2,2 попадания.
33. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.
Ответ. 2 детали.
34. Найти математическое ожидание произведения числа очков, которые могут выпасть при одном бросании двух игральных костей.
Ответ.12,25 очка.
35. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по одному билету равна 0,3.
Ответ.6 билетов.
62
2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Разработка методов регистрации, описания и анализа статистических данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет специаль-
ной науки - математической статистики.
Рассмотрим типичные задачи математической статистики, часто встречаемые на практике.
1.Задача определения закона распределения случайной величины по статистическим данным.
При обработке большого объема статистических данных часто возникает вопрос об определении законов распределения случайных величин. Поскольку на практике приходится иметь дело с ограниченным количеством экспериментальных данных, то результаты наблюдений и обработки всегда содержат элемент случайности. Тогда возникает вопрос о том, какие черты наблюдаемого явления относятся к постоянным, действительно присущим ему, а какие являются случайными и проявляются только за счет ограничения экспериментальных данных. Поэтому к методике обработки данных необходимо предъявлять такие требования, чтобы она сохраняла все типичные черты явления и отбрасывала все второстепенные, несущественные, связанные с ограниченным объемом опытного материала. В связи с этим возникает задача сглаживания или выравнивания статистических данных.
2. Задача проверки правдоподобия гипотез.
Так как статистический материал всегда ограничен, то выявляющиеся в нем статистические закономерности не лишены случайностей и статистический материал может лишь с большим или с меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы.
63
3.Задача нахождения неизвестных параметров распределения.
Часто при обработке экспериментальных данных характер закона распределения случайных величин качественно известен до опыта, а требуется определить некоторые параметры (числовые характеристики) случайной величины. При небольшом числе опытов такая задача не может быть определена точно, поскольку экспериментальный материал, а соответственно и все его параметры содержат элемент случайности. Поэтому может ставиться задача лишь об определении «оценок» или «подходящих значений» для искомых параметров, то есть таких приближенных значений, которые при массовом применении приводили бы в среднем к меньшим ошибкам, чем всякие другие.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Математическая статистика – это наука о принятии решений в условиях неопределенности.
2.1.Генеральная совокупность, выборка
Встатистике часто приходится исследовать распределение того или иного признака для весьма большой совокупности индивидуумов, образующих статистический коллектив (длина или вес тела какого-либо из группы животных; стандартность или размер детали из их большого числа). Данный признак является случайной величиной, значение которого меняется от индивидуума к индивидууму или от детали к детали. Однако чтобы составить представление о распределении этой случайной величины или о ее важнейших характеристиках, нет необходимости исследовать каждый индивидуум,
64

можно исследовать некоторую выборку достаточно большого объема для того, чтобы в ней были выявлены существенные черты изучаемого распределения. Совокупность, из которой производится выборка, называется генеральной совокупно- стью. При этом предполагается, что число членов N в генеральной совокупности весьма велико, а число членов n в выборке существенно меньше.
При составлении выборки можно поступать двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В связи с этим выборки подразде-
ляют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того чтобы выборка правильно отражала все черты генеральной совокупности, она должна быть репрезентативной (представительной). Выборка будет репрезентативной, если каждый ее объект отобран случайно из генеральной совокупности, а все объекты имеют одинаковую вероятность попасть в выборку.
Существуют следующие способы отбора.
1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: простой случайный беспо-
вторный отбор; простой случайный повторный отбор. Про-
стым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами. Например, для извлечения n объектов из генеральной совокупно-
65
сти объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад достают одну карточку. Объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют. В итоге получают простую случайную повторную выборку объема n. Если извлеченные карточки не возвращаются в пачку, то выборка является простой случайной бесповторной.
При большом объеме генеральной совокупности пользуются готовыми таблицами «случайных чисел», в которых числа расположены в случайном порядке. Для того чтобы отобрать, например 50 объектов из пронумерованной генеральной совокупности, открывают любую страницу таблицы случайных чисел и выписывают подряд 50 чисел. В выборку попадают те объекты, номера которых совпадают с выписанными случайными числами. Если случайное число таблицы превышает N, это число пропускают. При осуществлении бесповторной выборки случайные числа таблицы, встречающиеся ранее также пропускают.
2. Отбор, при котором генеральная совокупность разби-
вается на части: типический отбор; механический отбор; серийный отбор.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если продукция изготавливается на нескольких машинах, среди которых есть более или менее изношенные. В этом случае отбор производится не из всех деталей, а из продукции каждого станка в отдельности.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на несколько групп, столько, сколько объектов должно войти в выборку, а из каж-
66
дой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отбирают каждую пятую деталь. Такой отбор может не обеспечить репрезентативности выборки.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станковавтоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Этот отбор применяют тогда, когда обследуемый признак колеблется в различных сериях незначительно.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные способы. Например, разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий, а затем из каждой серии простым случайным отбором извлекают отдельные объекты.
При достаточно большом числе членов генеральной совокупности N оказывается, что свойства выборочных (статистических) распределений и характеристик практически не зависят от N, отсюда вытекает математическая идеализация, состоящая в том, что генеральная совокупность, из которой осуществляется выбор, имеет бесконечный объем. При этом отличают точные характеристики (закон распределения, математическое ожидание, дисперсию и т.д.), относящиеся к генеральной совокупности, от аналогичных им «выборочных» характе-
ристик. Выборочные характеристики отличаются от соответствующих характеристик генеральной совокупности за счет ограниченности объема выборки n. При неограниченном увеличении n все выборочные характеристики приближаются к соответствующим характеристикам генеральной совокупности.
67
2.2. Статистический ряд. Гистограмма
Пусть изучается некоторая случайная величина X, закон распределения которой в точности неизвестен, и требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величина X подчинена тому или иному закону. С этой целью над величиной X проводится ряд независимых опытов (наблюдений). В каждом из этих опытов случайная величина X принимает определенное значение. Совокупность наблюдаемых значений величины представляет собой первичный статистический материал, подлежащий обработке. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». Одним из способов обработки простого статистического ряда является построение статистической функцией распределе-
ния случайной величины.
Статистической функцией распределения случайной ве-
личины X называется частота события X < x в данном статистическом материале
F* x P* X x .
Для того чтобы найти значение статистической функции распределения при данном x, достаточно подсчитать число опытов, в которых величина X приняла значение, меньшее, чем x, и разделить на общее число n проведенных опытов.
Статистическая функция распределения любой случайной величины – прерывной или непрерывной – представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюдаемым значениям случайной величины и по величине равны частотам этих значений.
При увеличении числа опытов n статистическая функция распределения F* x
распределения F x случайной величины X.
68

Построение статистической функции распределения уже решает задачу описания экспериментального материала. Однако при большом числе опытов простая статистическая совокупность становится слишком громоздкой и мало наглядной. Статистический материал должен быть подвергнут дополнительной обработке – строится так называемый «статистический ряд». Весь диапазон наблюдаемых значений X делится на интервалы или «разряды» и подсчитывается количество значений ni , приходящееся на каждый i-й разряд. Это число делит-
ся на общее число наблюдений n и находится относительная частота, соответствующая данному разряду:
Pi* nni .
Сумма относительных частот всех разрядов равна едини-
це.
Таблица, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие относительные частоты называется статистическим рядом:
Таблица 1
Ii |
x1;x2 |
x2;x3 |
. . . |
|
xi;xi+1 |
. . . |
xk;xk+1 |
|
|
|
|
|
|
|
|
pi* |
p1* |
p2* |
. . . |
|
pi* |
. . . |
pk* |
|
|
|
|
|
|
|
|
Здесь Ii – обозначение I- го разряда; |
xi;xi+1 – |
его границы; pi* - |
|||||
соответствующая относительная частота; k – число разрядов.
Значение, находящееся в точности на границе двух разрядов считают в равной степени принадлежащем к обоим разрядам и прибавляют к числам ni того и другого разряда по ½.
Число разрядов, на которые следует группировать статистический материал не должно быть слишком большим, (ряд становится невыразительным) и слишком маленьким (свойства распределения описываются слишком грубо). Рационально выбирать число разрядов 10 - 20. Длины разрядов могут быть
69
как одинаковыми, так и разными. Кроме того, согласно формуле Стреджеса, рекомендуемое число интервалов разбиения
k 1 log 2 n , |
а |
длины |
частичных |
интервалов |
h xmax xmin / k . |
|
|
|
|
Наблюдения, упорядоченные по возрастанию, называют вариационным рядом. Его члены обычно обозначают xi и на-
зывают вариантами. Когда мы наблюдаем дискретную случайную величину, она может принимать одни и те же значения много раз. Число, показывающее, сколько раз появилось данное значение, называют частотой и обозначают ni .
Выборка в случае дискретных случайных величин может быть изображена в виде полигона частот или полигона отно-
сительных частот. Полигоном частот называют ломаную, отрезки которой соединяют точки x1; n1 , x2 ; n2 , …, xk ; nk ,
относительных частот – соответственно точки xi ; pi .
Статистический ряд часто оформляется в виде так назы-
ваемой гистограммы относительных частот (изображение выборки непрерывных случайных величин). Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как на основании строится прямоугольник, площадь которого равна относительной частоте данного разряда. В качестве высоты прямоугольника берется относительная частота разряда, деленная на его длину. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Полная площадь гистограммы равна единице.
При увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Эта кривая представляет собой график плотности распределения величины Х.
70
При построении гистограмм в реальных исследованиях следует понимать, что формула Стерджеса для числа интервалов разбиения дает лишь рекомендацию, а не строгое правило. Проблема выбора этого числа заключается в следующем. При слишком малых k гистограмма получается слишком грубой, «смазанной», плохо отражающей свойства распределения. При слишком больших k гистограмма становится «колючей» и, в конце концов, распадается на отдельные «иглы» (узкие столбцы) вперемешку с пустыми интервалами. Оптимальное значение в общем случае неизвестно - оно зависит как от типа распределения, так и от конкретной выборки. Что касается концов интервалов и значений вариант, то для человеческого восприятия более удобно, чтобы они выражались более или менее «круглыми» числами.
Гистограммы обычно строят на компьютере. Исследователь легко может варьировать параметры гистограммы и выбрать тот вариант, при котором график выглядит наилучшим образом.
Пример. 2.1. Анализируется выборка из 100 малых предприятий региона. Цель обследования - измерение коэффициента соотношения заемных и собственных средств ( xi ) на каж-
дом i-м предприятии. Результаты измерений представлены в табл. 2.
|
|
Требуется построить гистограмму и график накопленных |
|||
частот. |
|
|
|
||
|
|
Решение. Построим сгруппированный ряд наблюдений |
|||
(табл.3). |
|
|
|
||
2. |
Определим в выборке xmin 5,05 и xmax 5,85. |
||||
3. |
Разобьем весь диапазон xmin , xmax на k равных интервалов: |
||||
k 1 log 2 100 7,62; k 8, отсюда длина интервала |
|||||
h |
xmax xmin |
|
5,85 5,05 |
0,1. |
|
|
|
||||
|
|
k |
8 |
|
|
71
Таблица 2
Коэффициенты соотношений заемных и собственных средств предприятий
5,56 |
5,45 |
5,48 |
5,45 |
5,39 |
5,37 |
5,46 |
5,59 |
5,61 |
5,31 |
5,46 |
5,61 |
5,11 |
5,41 |
5,31 |
5,57 |
5,33 |
5,11 |
5,54 |
5,43 |
5,34 |
5,53 |
5,46 |
5,41 |
5,48 |
5,39 |
5,11 |
5,42 |
5,48 |
5,49 |
5,36 |
5,40 |
5,45 |
5,49 |
5,68 |
5,51 |
5,50 |
5,68 |
5,21 |
5,38 |
5,58 |
5,47 |
5,46 |
5,19 |
5,60 |
5,63 |
5,48 |
5,27 |
5,22 |
5,37 |
5,33 |
5,49 |
5,50 |
5,54 |
5,40 |
5,58 |
5,42 |
5,29 |
5,05 |
5,79 |
5,79 |
5,65 |
5,70 |
5,71 |
5,85 |
5,44 |
5,47 |
5,48 |
5,47 |
5,55 |
5,67 |
5,71 |
5,73 |
5,05 |
5,35 |
5,72 |
5,49 |
5,61 |
5,57 |
5,69 |
5,54 |
5,39 |
5,32 |
5,21 |
5,73 |
5,59 |
5,38 |
5,25 |
5,26 |
5,81 |
5,27 |
5,64 |
5,20 |
5,23 |
5,33 |
5,37 |
5,24 |
5,55 |
5,60 |
5,51 |
|
|
|
|
|
|
|
|
|
|
Таблица 3
Сгруппированный ряд наблюдений
Номер |
Интервалы |
Середины |
wi |
wic |
f n x |
интервала |
|
интервалов |
|
|
|
|
|
xi |
|
|
|
1 |
5,05-5,15 |
5,1 |
0,05 |
0,05 |
0,5 |
2 |
5,15-5,25 |
5,2 |
0,08 |
0,13 |
0,8 |
3 |
5,25-5,35 |
5,3 |
0,12 |
0,25 |
1,2 |
4 |
5,35-5,45 |
5,4 |
0,20 |
0,45 |
2,0 |
5 |
5,45-5,55 |
5,5 |
0,26 |
0,71 |
2,6 |
6 |
5,55-5,65 |
5,6 |
0,15 |
0,86 |
1,5 |
7 |
5,65-5,75 |
5,7 |
0,10 |
0,96 |
1,0 |
8 |
5,75-5,85 |
5,8 |
0,04 |
1,00 |
0,4 |
72

Относительная частота, %
30
25
20
15
10
5
0
5,0 |
5,1 |
5,2 |
5,3 |
5,4 |
5,5 |
5,6 |
5,7 |
5,8 |
5,9 |
Наблюдения
Рис. 4
На рис. 4, построенном по данным табл. 3, представлена гистограмма частот. Кривая соответствует плотности нор-
мального распределения, «подобранного» к данным.
2.3.Числовые характеристики статистического распределения. Обработка опытов
Для того чтобы найти закон распределения, необходимо располагать обширным статистическим материалом, порядка нескольких сотен опытов. Однако на практике, в силу дороговизны постановки опытов, чаще приходится иметь дело с двумя – тремя десятками наблюдений, а этого не достаточно для того, чтобы найти заранее неизвестный закон распределения
73
случайной величины. Но этот материал может быть обработан, и на его основе получены некоторые сведения о случайной величине, такие, как ее числовые характеристики: математическое ожидание, дисперсия.
С другой стороны, как часто бывает на практике, вид закона распределения заранее известен, но необходимо найти некоторые параметры, от которых он зависит, скажем, то же математическое ожидание и среднее квадратическое отклонение (для нормального закона распределения).
Рассмотрим, как найти неизвестные параметры, от которых зависит закон распределения случайной величины, по ограниченному числу опытов.
Ранее мы рассмотрели числовые характеристики случайных величин: математическое ожидание и дисперсию. Аналогичные числовые характеристики существуют и для статистических распределений. Каждой случайной величине Х соответствует ее статистическая аналогия.
Любое значение параметра, вычисленное на основе ограниченного числа опытов, всегда содержит элемент случайности. Такое приближенное, случайное значение называют оцен-
кой параметра.
Для математического ожидания случайной величины статистической аналогией является среднее арифметическое наблюдаемых значений случайной величины:
|
n |
|
|
М * X |
xi |
|
|
i 1 |
, |
||
n |
|||
|
|
где xi – значение случайной величины, наблюдаемое в i–м опыте, n - число опытов. В дальнейшем эту характеристику будем называть статистическим средним случайной величи-
ны, или выборочным средним
74

n
ni xi xв i 1 ,
n
где ni - частота появления значения xi .
В дальнейшем статистические аналогии будем снабжать значком *.
Статистическая дисперсия случайной величины Х:
|
n |
m*x 2 |
|
D * X |
xi |
||
i 1 |
|
, |
|
|
|
||
|
|
n |
|
где m* M * X - статистическое среднее, или выборочная |
|||||
x |
|
|
|
|
|
дисперсия |
|
|
|
|
|
|
n |
|
|
|
|
|
ni xi |
xв 2 |
|||
D |
i 1 |
|
. |
||
|
|
||||
в |
n |
|
|
|
|
|
|
|
|
|
|
Для удобства вычислений используют формулу
|
n |
|
n x2i |
|
i |
D |
i 1 |
|
|
в |
n |
|
|
n |
2 |
|
|
ni xi |
||
|
i 1 |
. |
|
n |
|||
|
|
||
|
|
|
|
|
|
|
|
При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близко к математическому ожиданию. Если число опытов невелико, то замена математического ожидания средним арифметическим приводит к ошибке, которая тем больше, чем меньше число опытов. Так же и с оценками других параметров. Любая из оценок случайна, и при пользовании ею неизбежны ошибки. Необходимо выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.
75
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.
Пусть — статистическая оценка неизвестного параметра теоретического распределения. Допустим, что по
выборке объема п найдена оценка 1 . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку 2 . Повторяя
опыт многократно, получим числа 1 , 2 , ..., которые, вообще говоря, различны между собой. Таким образом, оценкуможно рассматривать как случайную величину, а числа1 , 2 , ... , — как ее возможные значения.
Представим себе, что оценка дает приближенное значение с избытком; тогда каждое найденное п о д а н н ым
выборок число i (i=1, 2, . . ., k) больше истинного значения . Ясно, что в этом случае и математическое ожидание
(среднее значение) случайной величины больше, чем , т. е.
М ( ) > . Очевидно, что если дает оценку с недостатком, то М ( )< .
Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. По этой причине естественно потребовать, чтобы матема-
тическое ожидание оценки было равно оцениваемому параметру. Хотя соблюдение этого требования не устранит
ошибок (одни значения больше, а другие меньше ), однако ошибки разных знаков будут встречаться одинаково часто.
Иными словами, соблюдение требования М ( ) = гарантирует от получения систематических ошибок.
76

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру
при любом объеме выборки, т. е. М ( ) = . Смещенной называют оценку, математическое ожидание
которой не равно оцениваемому параметру.
Однако было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого пара-
метра. Действительно, возможные значения могут быть сильно рассеяны вокруг своего среднего значения, т. е. дис-
персия D ( ) может быть значительной. В этом случае най-
денная по данным одной выборки оценка, например , может оказаться весьма удаленной от среднего, а значит, и от са-
мого оцениваемого параметра . Приняв в качестве приближенного значения , мы допустили бы большую ошибку.
Если же потребовать, чтобы дисперсия была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требова-
ние эффективности.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (п велико!) к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при п стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при пстремится к нулю, то такая оценка оказывается и состоятельной.
Выборочная средняя в ~ является состоятельной x m
оценкой генерального среднего или математического ожидания, поскольку при неограниченном числе опытов выборочное среднее приближается к математическому ожиданию, и не-
77

смещенной оценкой, так как математическое ожидание от вы-
борочной средней есть математическое ожидание случайной
~
величины X: M m m . При ограниченном числе опытов вы-
борочное среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем представление.
Дисперсия этой оценки равна:
~ 1 .
D m n D
Эффективность или неэффективность оценки зависит от вида закона распределения величины Х. Если величина Х рас-
пределена по нормальному закону, то дисперсия будет мини-
~
мально возможной, то есть оценка m является эффективной. Для других законов распределения это может быть не так.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии. Для оценки дисперсии будем использо-
вать так называемую «исправленную» выборочную дисперсию,
которая является состоятельной и несмещенной.
|
|
n |
|
~ 2 |
|
|
|
|
|
|
|
|
|
|
|
n x2i n x |
|
|
|
||
~ |
|
ni xi m |
2 |
/ n |
|
|||||
D |
i 1 |
|
|
= |
i |
i i |
|
|
. |
|
|
n 1 |
|
|
n 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
Оценка |
~ |
для дисперсии не является эффективной, од- |
||||||||
D |
||||||||||
нако для нормального |
закона распределения |
она является |
||||||||
«асимптотически эффективной», то есть при увеличении n отношение дисперсии к минимально возможной неограниченно приближается к единице.
Пример. 2.2. Найти выборочное среднее по выборке объ-
ема n=20:
Таблица 4
xi |
2560 |
2600 |
2620 |
2650 |
2700 |
ni |
2 |
3 |
10 |
4 |
1 |
|
|
|
|
|
|
|
|
78 |
|
|
|

Решение. Для упрощения расчетов перейдем к условным
вариантам ui |
xi |
2620 : |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 5 |
||
|
|
|
|
|
ui |
|
-60 |
-20 |
0 |
30 |
|
80 |
|
|
|
|
|
|
ni |
|
2 |
3 |
10 |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
в |
2 60 3 20 10 0 1 80 20 1 и |
|||||||||
u |
|||||||||||||
xв 2620 |
|
в |
2621. |
|
|
|
|
|
|
||||
u |
|
|
|
|
|
|
|||||||
Замечание. В качестве числа, которое вычитывается при переходе к условным вариантам (условный нуль), обычно выбирается варианта, стоящая в середине ряда, либо та, для которой частота максимальна. В данном примере они совпадают.
Пример. 2.3 Найти неисправленную выборочную дисперсию по выборке объема n=50:
|
|
|
|
|
|
|
|
|
|
|
Таблица 6 |
||
|
xi |
|
18,4 |
|
|
18,9 |
|
19,3 |
19,6 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
5 |
|
|
|
|
10 |
|
20 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. |
Перейдем |
к |
условным |
вариантам |
|||||||||
ui 10 xi 19,3 . |
|
Тогда |
|
по |
свойству |
дисперсии |
|||||||
Dui D 10xi 193 100Dxi |
и |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 7 |
||
|
|
|
ui |
|
-9 |
|
-4 |
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni |
|
5 |
|
10 |
|
20 |
15 |
|
|
|
Найдем выборочную дисперсию для новой варианты ui
79
D u |
|
|
1 |
|
4 |
|
|
4 |
|
n |
u |
i |
|
2 |
||||
|
|
|
ni ui2 |
|
|
i |
|
|
|
|||||||||
n |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
n |
|
||||||
|
|
1 |
|
5 9 2 10 4 2 20 02 15 32 |
||||||||||||||
50 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
45 40 0 |
45 |
|
13,36. |
|||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
50 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда, переходя к первоначальной варианте xi , получаем
D x D u  100 13,36
100 13,36 100 0,1336.
100 0,1336.
Кроме выборочной средней и выборочной дисперсии применяются и другие характеристики вариационного ряда, такие как, мода – варианта, которая имеет наибольшую частоту, медиана – варианта, которая делит вариационный ряд на две части, равные по числу вариант и еще ряд других характеристик.
2.4. Доверительный интервал. Доверительная вероятность
Ранее был рассмотрен вопрос об оценке неизвестного параметра одним числом. Такая оценка называется «точечной». Однако в ряде задач требуется не только найти для параметра подходящее численное значение, но и оценить его точность и надежность. Требуется знать, к каким ошибкам может привести замена параметра его точечной оценкой
* , и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы?
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка * в значительной мере
случайна и приближенная замена на * может привести к серьезным ошибкам.
80

Чтобы дать представление о точности и надежности
оценки * , в математической статистике пользуются так на-
зываемыми доверительными интервалами и доверительными вероятностями.
При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая ха-
рактеристика * служит оценкой неизвестного параметра .
Ясно, что * тем точнее определяет параметр , чем меньше абсолютная величина разности * . Другими словами, ес-
ли |
* |
< , то чем меньше |
, тем оценка точнее. Таким |
образом, положительное число |
характеризует точность |
||
оценки. |
|
|
|
Однако статистические методы не позволяют категори-
чески утверждать, что оценка * удовлетворяет неравенству* < ; можно лишь говорить о вероятности , с кото-
рой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки
по * |
|
называют вероятность , с которой осуществляется |
|
|
* |
|
< . Обычно надежность оценки задается наперед, |
|
|
||
при чем в качестве берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999. Пусть
81

вероятность того, что |
|
|
* |
|
< , равна : P |
* |
|
. |
|
|
|
|
|
||||||
Заменив неравенство |
|
* |
|
|
< равносильным ему двойным |
||||
|
|
|
|||||||
неравенством * , или * * , имеем
P * * .
Вероятность того, что интервал * , * заключает в себе (покрывает) неизвестный параметр , равна .
Доверительным называют интервал * , * , который покрывает неизвестный параметр с заданной надежностью .
Тогда диапазон практически возможных значений ошиб-
ки, возникающей при замене на * , будет , а большие по величине ошибки будут появляться лишь с малой вероятностью 1 , а неизвестное значение параметра попадает в
интервал
|
|
* |
|
|
|
|
|
I |
|
|
; |
|
|
|
|
* .
Величина рассматривается не как вероятность «попадания» точки в интервал I , а как вероятность того, что случайный интервал I накроет точку (рис. 2).
I


|
|
|
|
|
|
|
|
|
|
||||
0 |
|
1 |
2 |
|||
|
|
|||||
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5
Вероятность называют доверительной вероятностью,
82
а интервал I - доверительным интервалом. Границы интер-
вала I : 1 * и 2 * называются доверитель-
ными границами.
Пусть произведено n независимых опытов над случайной величиной Х, характеристики которой – математическое ожидание m и дисперсия D – неизвестны. Для этих параметров получены оценки:
|
n |
|
|
n |
m |
|
|
m |
|
|
xi |
||
|
|
|
|
|
~ 2 |
|
~ |
i 1 |
|
~ |
i 1 |
|
|
m |
|
; |
D |
|
|
. |
|
|
|
||||
|
n |
|
|
n |
1 |
|
Требуется построить доверительный интервал I , соответствующий доверительной вероятности (заданной), для математического ожидания m и дисперсии D величины Х.
Исходим из того, что величины ~ и ~ распределены по m D
нормальному закону. Характеристики этого закона – математическое ожидание и дисперсия – равны соответственно а и
|
D |
. Предположим, что дисперсия D известна. Найдем такую |
|||||||||
|
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
величину , для которой |
|
|
|
|
|
|
|
||||
|
|
P |
|
~ |
a |
|
. |
|
|
||
|
|
|
|
|
|
||||||
|
|
|
m |
|
|
|
|||||
|
|
Используем формулу для вычисления вероятности за- |
|||||||||
данного отклонения |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
a |
|
a |
|||
|
|
P X Ф |
|
|
Ф |
|
, |
||||
|
|
|
|
|
|
|
|
|
|||
а именно
83

P |
|
X a |
|
P a X a |
|||||||||
|
|
||||||||||||
|
|
|
a a |
|
а а |
|
|||||||
Ф |
|
|
|
|
|
Ф |
|
|
|
||||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
Ф |
|
|
Ф |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Приняв во внимание тот факт, что функция Лапласа – не- |
|||||||||||||
четная, имеем P |
|
X a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||
|
2Ф |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
n , получим |
|
|||||||||||
|
Заменив X на m , а |
на m / |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
2Ф n / 2Ф t , |
|
|||||||||||||
|
|
|
|
|
|
|
m a |
|
||||||||||||||
где |
|
- среднее квадратическое отклонение оценки |
~ |
|||||||||||||||||||
m , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
n / . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Отсюда t / |
|
|
|
|
|
||||||||||||||||
|
n , а, приняв во внимание, что вероят- |
|||||||||||||||||||||
ность Р задана и равна , то окончательно имеем |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
P m t / n |
a m t / n 2Ф t . |
|
|||||||||||||||
|
Таким образом, с вероятностью |
(надежностью) можно |
||||||||||||||||||||
утверждать, |
|
что |
|
доверительный |
|
|
интервал |
I = |
||||||||||||||
~ |
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n, |
|
|
|
n |
покрывает неизвестный параметр а; |
|||||||||||||
m t / |
|
m t / |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точность оценки t / |
|
n . Число t определяется из равенст- |
||||||||||||||||||||
ва 2Ф t |
или Ф t |
|
. По таблице функции Лапласа (табл. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 приложения) находят аргумент t, которому соответствует значение функции Лапласа, равное 2 .
84

Пример. 2.4. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением 3 . Найти доверительные интервалы для оценки неизвестного математического ожидания a по выборочным средним xв , если объем выборки n=36 и задана надежность
оценки 0,95 .
Решение. Найдем t. Из соотношения 2 t 0,95 получим t 0,475. По таблице функции Лапласа находим t=1,96.
Найдем точность оценки:
= t / 
 n 1,96 3 /
n 1,96 3 / 
 36 0,98.
36 0,98.
Доверительный интервал таков: xв 0,98; xв 0,98 .
Поясним смысл, который имеет заданная надежность. Надежность 0,95 указывает, что если произведено доста-
точное большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.
Предположим теперь, что дисперсия D неизвестна.
Тогда доверительный интервал для математического
ожидания находится |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|
|
~ |
|
~ |
||||
|
|
n, |
|
|
||||||||||||
I = m t |
D / |
|
m t |
D / |
n , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где величина t определяется из условия |
||||||||||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
t |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
m a |
|
|
2 Sn 1 t dt |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
P |
|
|
~ |
|
|
|
|
|
|
t |
|||||
|
|
|
|
D / |
n |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
||||||||||
и находится из таблицы распределения Стьюдента (табл. 2
85

приложения).
Здесь Sn 1 t плотность закона распределения Стьюдента
с n-1 степенями свободы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
||||
|
|
Г |
|
|
|
|
|
t |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
||||||||||
Sn 1 t |
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
||||
|
|
n 1 Г |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
где Г x - гамма –функция: |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Г x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x 1e u du . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доверительный интервал для дисперсии, покрывающий точку D с вероятностью , находится
|
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
|
|
D n 1 |
|
D n 1 |
|
|
|||
|
|
I |
|
|
|
; |
|
|
, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
где 2 |
и 2 |
- критические точки 2 («хи-квадрат») распреде- |
|||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
ления с n-1 степенями свободы и соответствующими |
|
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
уровнями значимости, 1 , |
n – объем выборки. |
|||||||||
Критические точки находят по таблице критических точек распределения «хи-квадрат» (табл. 3 приложения).
Можно также по выборке x1, x2 ,..., xn построить довери-
тельный интервал для следующего (n+1)-го, наблюдения (то есть определить границы, в которых оно будет лежать с заданной вероятностью), а именно имеем
~ |
~ |
|
1 |
~ |
~ |
|
1 |
|
|
|
m t |
D 1 |
|
|
|
xn 1 m t |
D 1 |
|
|
. |
|
|
|
|||||||||
|
|
|
n |
|
|
|
n |
|||
|
|
|
|
|
86 |
|
|
|
|
|

Понятно, что это может быть полезно в качестве прогноза на будущее.
Пример. 2.5. Из генеральной совокупности извлечена выборка объема n = 12:
Таблица 8
Варианта |
-0,5 |
-0,4 |
-0,2 |
0 |
0,2 |
0,6 |
0,8 |
1 |
1,2 |
1,5 |
xi |
|
|
|
|
|
|
|
|
|
|
Частота |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
ni |
|
|
|
|
|
|
|
|
|
|
Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
Решение. |
Найдем выборочное среднее xв и исправлен- |
|||||||||||||||||||
ное выборочное среднее квадратическое отклонение |
~ |
|||||||||||||||||||
D . Пусть |
||||||||||||||||||||
условные варианты ui |
10xi , тогда |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
1 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,2 |
|
|
|
|
u |
в |
0,42 ; |
|
||||||
|
u |
в |
|
n u |
i |
; x |
в |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
n i 1 |
i |
|
|
|
|
|
10 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
~ |
|
|
|
1 |
|
|
10 |
|
|
1 10 |
|
|
|
|
2 |
|
||||
D |
|
|
|
|
|
n x2 |
|
n x |
|
|
0,52 . |
|
||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
n i 1 |
|
i i |
n i 1 |
|
i |
i |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для уровня значимости 0,05 и числа степеней свободы n 1 11 по таблице распределения Стьюдента находим критическую точку t =2,2 и определяем границы доверитель-
ного интервала:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
~ |
|
|
|
2,2 0,72 |
|
|
||||
x |
|
|
|
D |
|
0,42 |
|
0,04 |
; |
|||||
в |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
n |
12 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
~ |
|
|
|
2,2 0,72 |
|
||||
x |
|
|
|
D |
|
0,42 |
|
0,88 . |
|||||
в |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
n |
12 |
|
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Таким образом, искомый доверительный интервал:
0,04 a 0,88.
Пример. 2.6. Для отрасли, включающей 1200 фирм, составлена случайная выборка из 19 фирм. По выборке оказалось, что исправленное среднее квадратическое отклонение
~
для числа работающих на фирме составляет  D =25 (человек). пользуясь 90% -ым доверительным интервалом, оценить среднее квадратическое отклонение для числа работающих на фирме по всей отрасли, построив доверительный интервал.
D =25 (человек). пользуясь 90% -ым доверительным интервалом, оценить среднее квадратическое отклонение для числа работающих на фирме по всей отрасли, построив доверительный интервал.
Решение. Доверительный интервал для параметра имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
~ |
|
|
|
|
|
||
|
|
|
|
|
|
D n 1 |
|
|
D n 1 |
, |
|
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
где |
2 |
и |
2 |
находят по таблице критических точек распреде- |
||||||||||||||
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ления |
хи-квадрат. По |
|
таблице |
определяем 2 |
= 28,9 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0,95; n 1 |
|
|
||
|
2 |
0,05; n 1 18 ; |
2 |
= 9,39 1 |
2 |
18 . Под- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ставляя в формулу необходимые величины, получаем искомый доверительный интервал 25
 18
18 28,9 25
28,9 25
 18
18 9,39, откуда
9,39, откуда
19,74 34,61 (человек).
Пример. 2.7. За последние 5 лет годовой рост актива А составлял в среднем 20% со средним квадратическим отклонением (исправленным) 5%. Построить доверительный интервал
88

с вероятностью 95% для цены актива в конце следующего года, если в начале года она равна 100 ден.ед.
Решение. Рассмотрим величины относительного прироста цены актива за год. Будем пользоваться нормальным приближением. Применяем формулу
|
|
~ |
1 |
|
|
|
~ |
1 |
|
|||||
xв t |
|
D 1 |
|
|
xn 1 |
xв t |
D 1 |
|
, |
|||||
|
|
|||||||||||||
|
|
|
|
n |
|
|
|
|
|
n |
||||
где t находим из |
таблицы |
распределения |
|
Стьюдента: |
||||||||||
t tkp ; n 1 tкр 0,05;4 2,78 . |
|
|
|
|
|
|
||||||||
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0.2 0,05 2,78 |
1,2 x 6 |
0,2 0,05 2,78 |
1,2 , |
|
|
|
||||||||
откуда 0,05 x6 |
0,35 . |
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, цена актива в следующем году составит от 105 до 135 ден.ен.
2.5. Методы расчета сводных характеристик выборки
Пусть варианты выборки располагаются в виде вариационного ряда.
Условными называют варианты, определяемые равенст-
вом
ui xi C / h ,
где С – ложный нуль (новое начало отсчета); h – шаг (разность между любыми двумя соседними первоначальными вариантами, новая единица масштаба).
Упрощенные методы расчета сводных характеристик выборки основаны на замене первоначальных вариант условны-
89
ми.
Рассмотрим методику вычисления выборочных характеристик для равноотстоящих вариант.
Метод произведений дает удобный способ вычисления выборочной средней и выборочной дисперсии. Целесообразно пользоваться расчетной таблицей, которая составляется так:
1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;
2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;
3) в третий столбец записывают условные варианты ui xi C / h , причем в качестве ложного нуля С выбирают
варианту, которая расположена примерно в середине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клетках над нулем пишут последовательно —1, —2, —3 и т.д., а под нулем—1,
2, 3 и т.д.; 4) умножают частоты на условные варианты и запи-
сывают их произведения niui в четвертый столбец; сложив все полученные числа, их сумму niui помещают в ниж-
нюю клетку столбца; 5) умножают частоты на квадраты условных вариант и
записывают их произведения niui2 в пятый столбец; сложив
все полученные числа, их сумму n u 2 |
помещают в ниж- |
i i |
|
нюю клетку столбца; 6) умножают частоты на квадраты условных вариант,
увеличенных каждая на единицу, и записывают произве-
90
дения ni ui 1 2 в шестой контрольный столбец; сложив все
полученные числа, их сумму ni ui 1 2 помещают в ниж-
нюю клетку столбца; 7) вычисляют выборочные среднюю и дисперсию:
xв niui h / n C ; Dв niui2 / n niui / n 2 h2 .
Пример. 2.8. Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:
варианты |
10,2 |
10,4 |
10,6 |
10,8 |
11,0 |
11,2 |
11,4 |
11,6 11,8 12,0 |
|||
частоты |
2 |
3 |
8 |
13 |
25 |
20 |
12 |
|
10 |
6 |
1 |
Решение. Составим расчетную таблицу, |
для чего: |
|
|||||||||
1)запишем варианты в первый столбец;
2)запишем частоты во второй столбец; сумму частот
(100)поместим в нижнюю клетку столбца;
3)в качестве ложного нуля выберем варианту 11,0 (эта варианта расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем записываем последовательно –1, –2, –3, –4, а под нулем
—1 , 2, 3, 4, 5;
4)произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму (-46) отрицательных и отдельно сумму (103) положительных чисел; сложив эти числа, их сумму (57) помещаем в нижнюю клетку столбца;
5)произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца;
91

6) произведения частот на квадраты условных вариант, увеличенных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца.
В итоге получим расчетную таблицу 9.
Таблица 9
1 |
2 |
3 |
4 |
5 |
6 |
xi |
|
ni |
ui |
niui |
|
n |
u 2 |
n |
u |
i |
1 2 |
|
|
|
|
|
|
|
i |
i |
i |
|
|
|
|
10,2 |
2 |
–4 |
–8 |
32 |
|
|
18 |
|||||
|
|
|
|
|
|
|
|
|
|
|||
10,4 |
|
3 |
–3 |
–9 |
27 |
|
|
12 |
||||
|
|
|
|
|
|
|
|
|
|
|
||
10,6 |
|
8 |
–2 |
– 16 |
32 |
|
|
|
8 |
|||
|
|
|
|
|
|
|
|
|
|
|
||
10,8 |
|
13 |
–1 |
– 13 |
13 |
|
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
||
11,0 |
|
25 |
0 |
А1 = –46 |
|
|
|
|
|
25 |
||
11,2 |
|
20 |
1 |
20 |
|
20 |
|
|
80 |
|||
|
|
|
|
|
|
|
|
|
|
|||
11,4 |
|
12 |
2 |
24 |
|
48 |
|
|
108 |
|||
|
|
|
|
|
|
|
|
|
|
|||
11,6 |
|
10 |
3 |
30 |
|
90 |
|
|
160 |
|||
|
|
|
|
|
|
|
|
|
|
|||
11,8 |
|
6 |
4 |
24 |
|
96 |
|
|
150 |
|||
|
|
|
|
|
|
|
|
|
|
|||
12,0 |
|
1 |
5 |
5 |
|
25 |
|
|
36 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 =103 |
|
|
|
|
|
|
|
|
|
|
n=100 |
|
niui = |
|
n u 2 = 383 |
n u |
i |
1 2 |
|||
|
|
|
|
|
|
i i |
|
i |
|
|
|
|
|
|
|
|
57 |
|
|
|
=597 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем шаг: h 10,4 10,2 0,2. |
|
|
|
|
|
|
|||||
|
Вычислим искомые выборочные среднюю и дисперсию: |
|||||||||||
|
xв niui h / n C =(57/100)0,2+11,0=11,1; |
|
|
|
|
|||||||
|
|
|
Dв niui2 / n niui / n 2 |
h2 = |
|
|
|
|
||||
|
|
|
|
|
92 |
|
|
|
|
|
|
|
=(383/100- 0,57 2 ) 0,22 =0,14.
На практике данные наблюдений не являются равноотстоящими вариантами, поэтому интервал, в котором заключены все наблюдаемые значения признака, делят на несколько равных частичных интервалов, находят их середины. Середины интервалов и образуют последовательность равноотстоящих вариант.
2.6. Построение нормальной кривой по опытным данным
Один из способов построения нормальной кривой по данным наблюдений состоит в следующем:
1)находят xв и , например по методу произведений;
2)находят ординаты (выравнивающие частоты) теоре-
тической кривой по формуле = |
|
, где n – сумма на- |
|
блюдаемых частот; h – разность между двумя соседними вари-
антами: |
и |
|
|
; |
|
||||
3) строят точки |
|
в прямоугольной системе коорди- |
||
нат и соединяют их плавной кривой.
Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что обследуемый признак распределен нормально.
Для того, чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами – критериями согласия.
93
2.7. Проверка статистических гипотез
Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид (назовем его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, выдвигается гипотеза о виде предпола-
гаемого закона распределения.
Возможен случай, когда закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр равен определенному значению 0 , то вы-
двигают гипотезу: 0 . Таким образом, выдвигается гипотеза о
предполагаемой величине параметра одного известного распределе-
ния. Возможны и другие гипотезы.
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.
Например, статистическими являются гипотезы:
1) генеральная совокупность распределена по нормальному за-
кону;
2) дисперсии двух нормальных совокупностей равны между собой.
В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.
Гипотеза «на Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.
94
Нулевой (основной) называют выдвинутую гипотезу H 0 .
Конкурирующей (альтернативной) называют гипотезу H1 ,
которая противоречит нулевой.
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку производят статическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Подчеркнем, что последствия этих ошибок могут оказаться весьма различными. Например, если отвергнуто правильное решение «продолжать строительство жилого дома», то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей. Можно привести примеры, когда ошибка первого рода влечет более тяжелые последствия, чем ошибка второго рода.
Вероятность совершить ошибку первого рода принято обозначать через , ее называют уровнем значимости.
Для проверки нулевой гипотезы используют специально подобранную случайную величину, точное или приближенное распределение которой известно. Эту величину обозначают
через U или Z, если она распределена нормально, F или v 2 —
95
по закону Фишера — Снедекора, T - по закону Стьюдента, 2 —
по закону «хи - квадрат» и т. д.
Статистическим критерием (или просто критерием)
называют случайную величину K (обозначим так в целях общности), которая служит для проверки нулевой гипотезы.
Наблюдаемым значением Kнаблназывают значение критерия, вычисленное по выборкам.
После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая — при которых она принимается.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы (областью допустимых зна-
чений) называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез,
можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.
Критическая область и область принятия гипотезы являются интервалами и, следовательно, существуют точки, которые их разделяют.
Критическими точками (границами) K кр называют точки,
отделяющие критическую область от области принятия гипотезы.
Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
96

а) |
|
|
|
|
|
|
|
|
|
K |
|
|
|
0 |
|
|
K кр |
|
|
|
|
|
|
|
|
|
||||||
б) |
|
|
|
|
|
K |
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
K |
кр |
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
K |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
K кр |
|
|
|
K кр |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
Рис. 6 |
|||||
Правосторонней называют критическую область, определяемую неравенством K Kкр , где K кр — положительное число
(рис. 6, а).
Левосторонней называют критическую область, определяемую неравенством K Kкр , где K кр — отрицательное число
(рис. 6, б).
Односторонней называют правостороннюю или левостороннюю критическую область.
Двусторонней называют критическую область, определяемую неравенствами K K1кр , K K2кр , где K2кр K1кр .
Если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенством
K Kкр (рис. 6, в).
Для отыскания правосторонней или левосторонней критической области достаточно найти критическую точку.
Для ее нахождения задаются достаточно малой вероятностью – уровнем значимости . Затем ищут критическую точку K кр исходя из требования, чтобы при условии справедливости
нулевой гипотезы вероятность того, что критерий K примет зна-
97

чение, большее K кр , была равна принятому уровню значимости P K Kкр - для правосторонней области и P K Kкр
- для левосторонней области. Для отыскания критических точек двусторонней критической области служит соотношение
P K Kкр / 2 .
Для каждого критерия имеются соответствующие таблицы, по которым находят критическую точку, удовлетворяющую данному требованию.
Далее по данным выборок вычисляют наблюдаемое значение критерия, и если для правосторонней критической области окажется, что Кнабл Ккр , то нулевую гипотезу отвергают, если же Кнабл Ккр , то нет оснований, чтобы отвергнуть нулевую ги-
потезу. Для левосторонней критической области все наоборот.
Однако наблюдаемое значение критерия может оказаться большим K кр (для правосторонней критической области) не по-
тому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостаток методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости .
Пусть нулевая гипотеза принята; ошибочно думать, что тем самым она доказана. Правильно говорить «данные наблюдений согласуются с нулевой гипотезой и, следовательно, не дают оснований ее отвергнуть».
На практике для большей уверенности принятия гипотезы ее проверяют другими способами или повторяют эксперимент, увеличив объем выборки.
Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, ес-
98
ли верна конкурирующая гипотеза.
Критическую область следует строить так, чтобы мощность критерия была максимальной, что должно обеспечить минимальную ошибку второго рода, что, конечно, желательно.
Вероятность допустить ошибку второго рода равна 1- , поэтому одновременно уменьшить ошибки первого и второго рода невозможно. Следует делать выбор из соображений целесообразности.
Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок.
2.8. Сравнение двух дисперсий нормальных генеральных совокупностей
На практике задача сравнения дисперсий возникает, если требуется сравнить точность приборов, инструментов, самих методов измерений и т.д. Очевидно, предпочтительнее тот прибор, инструмент и метод, который обеспечивает наименьшее рассеяние результатов измерений, то есть наименьшую дисперсию.
Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам с объемами n1 и n2 ,
извлеченным из этих совокупностей, найдены исправленные
~ ~
выборочные дисперсии D1 и D2 . Требуется по исправленным
дисперсиям при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой или, что математические ожидания исправленных выборочных дисперсий равны между собой. Такая задача ставится потому, что обычно исправленные дисперсии оказываются различны-
99
ми. Возникает вопрос: значимо (существенно) или незначимо различаются исправленные дисперсии?
Если окажется, что нулевая гипотеза справедлива, то есть генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие исправленных выборочных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность.
Если нулевая гипотеза отвергнута, то есть генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными причинами, а является следствием того, что сами генеральные дисперсии различны. Например, если различие исправленных выборочных дисперсий результатов измерений, произведенных двумя приборами, оказалось значимым, то точность приборов различна.
В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий принимают отношение большей
исправленной дисперсии к меньшей, то есть случайную вели-
~ ~
чину F Dб / Dм .
Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера-Снедекора со степенями свободы k1 n1 1 и k2 n2 1, где n1 - объем выборки, по которой вычислена большая исправленная дисперсия, n2 -
объем выборки, по которой найдена меньшая дисперсия. Распределение Фишера-Снедекора зависит только от степеней свободы и не зависит от других параметров.
Критическая область строится в зависимости от вида конкурирующей гипотезы.
Правило 1. Для того чтобы при заданном уровне значи-
100
мости проверить нулевую гипотезу H0 : D x D y о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H1 : D x D y , надо вычислить
отношение Fнабл ~б ~м , по таблице критических точек
D
/
D
распределения Фишера-Снедекора, по заданному уровню значимости и числам степеней свободы k1 и k2 найти критическую точку Fкр ; k1, k2 .
Если Fнабл Fкр - нет оснований отвергнуть нулевую гипотезу. Если Fнабл Fкр - нулевую гипотезу отвергают.
Пример. 2.9. По двум независимым выборкам объемов
n1 =12 и n2 =15, извлеченным из нормальных генеральных со- |
||
вокупностей X и Y найдены исправленные выборочные дис- |
||
|
~ |
~ |
персии |
DX 11,41 и |
DY 6,52 . При уровне значимости |
0,05 |
проверить нулевую гипотезу о равенстве генераль- |
|
ных дисперсий при конкурирующей гипотезе H1 : D x D y . Решение. Найдем отношение большей исправленной
дисперсии к меньшей: |
Fнабл 11,41/ 6,52 1,75. |
|||||
По |
условию |
конкурирующая |
гипотеза имеет вид |
|||
D x D y , поэтому критическая область - правосторонняя. |
||||||
По таблице, по уровню значимости 0,05 и по числам |
||||||
степеней |
свободы |
k1 12 1 11, |
|
k2 15 1 14 находим |
||
|
|
|
|
|
|
2,56 . |
критическую точку |
F |
|
0,05; 11, 14 |
|
||
|
|
кр |
|
|
|
|
|
|
|
|
|
|
|
Так как Fнабл Fкр |
- нет оснований отвергнуть нулевую |
|||||
гипотезу о равенстве генеральных дисперсий.
Правило 2. Для того чтобы при заданном уровне значи- |
||
мости |
проверить нулевую гипотезу H0 : D x D y |
о ра- |
|
101 |
|
венстве генеральных дисперсий нормальных совокупностей |
|
при конкурирующей гипотезе H1 : D x D y , надо вычис- |
|
~ |
~ |
лить Fнабл Dб |
/ Dм , найти по таблице критическую точку |
Fкр / 2; k1, k2 . |
|
Если Fнабл Fкр - нет оснований отвергнуть нулевую гипотезу. Если Fнабл Fкр - нулевую гипотезу отвергают.
Пример. 2.10. По двум независимым выборкам, объемы
которых соответственно равны n1 =10 и |
n2 =18, извлеченных |
из нормальных генеральных совокупностей X и Y найдены ис- |
|
~ |
~ |
правленные выборочные дисперсии DX |
1,23 и DY 0,41. |
При уровне значимости 0,1 проверить нулевую гипотезу о равенстве генеральных дисперсий при конкурирующей гипо-
тезе H1 : D X D Y .
Решение. Найдем отношение большей исправленной дис-
персии к меньшей: |
Fнабл 1,23/ 0,41 3. |
|||
По |
условию |
конкурирующая |
гипотеза имеет вид |
|
D X D Y , поэтому критическая область - двусторонняя. |
||||
По таблице, по уровню значимости, вдвое меньшем за- |
||||
данного, то есть при / 2 0,1/ 2 0,05 |
и по числам степеней |
|||
свободы k1 10 1 9 , |
k2 18 1 17 находим критическую |
|||
|
|
|
2,50 . |
|
точку F |
0,05; 9, |
17 |
|
|
кр |
|
|
|
|
|
|
|
|
|
Так как Fнабл Fкр , нулевую гипотезу о равенстве генеральных дисперсий отвергаем. Другими словами, выборочные исправленные дисперсии различаются значимо. Например, если бы рассматриваемые дисперсии характеризовали точность двух методов измерений, то следует предпочесть тот метод, который имеет меньшую дисперсию (0,41).
102
2.9. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности
Пусть генеральная совокупность распределена нормально, причем генеральная дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотетическому (предполагаемому) значению D0 . На практике D0 устанавли-
вается на основании предшествующего опыта или теоретически.
Пусть из генеральной совокупности извлечена выборка
объема n и по ней найдена исправленная выборочная диспер- |
||
сия |
~ |
с k n 1 степенями свободы. Требуется по исправ- |
D |
||
ленной дисперсии при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению D0 . То есть требуется установить, значимо или не-
значимо различаются исправленная выборочная и гипотетическая генеральная дисперсии.
На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов. Например, если известно, что допустимая характеристика рассеяния контролируемого размера деталей, изготавливаемых станком-автоматом, равна D0 , а найденная по выборке
окажется значимо больше D0 , то станок требует подналадки.
В качестве критерия для |
проверки нулевой гипотезы |
|
принимается случайная величина |
2 |
~ |
n 1 D / D . |
||
|
|
0 |
Критическая область строится в зависимости от вида конкурирующей гипотезы.
103
Правило 1. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : D D0 о равенстве неизвестной генеральной дисперсии нормальной совокупности
гипотетическому |
значению при конкурирующей гипотезе |
|
H1 : D D0 , надо вычислить наблюдаемое значение критерия |
||
2 |
~ |
|
n 1 D / D и по таблице критических точек распреде- |
||
набл |
|
0 |
ления 2 , по заданному уровню значимости и числу степеней свободы k n 1 найти критическую точку кр2 ; k .
Если набл2 кр2 - нет оснований отвергнуть нулевую гипотезу (то есть различие между исправленной дисперсией и гипотетической генеральной дисперсией – незначимое). Если
2 |
|
|
2 - нулевую гипотезу отвергают. |
|||
набл |
|
кр |
|
|
|
|
|
Пример. 2.11. Из нормальной генеральной совокупности |
|||||
извлечена выборка объема |
n 13 |
и по ней найдена исправлен- |
||||
ная выборочная дисперсия |
~ |
|
||||
D =14,6. Требуется при уровне зна- |
||||||
чимости |
0,01 |
проверить нулевую гипотезу H0 : D D0 =12, |
||||
приняв в качестве конкурирующей гипотезы H1 : D 12 . |
||||||
|
Решение. |
Найдем |
наблюденное значение критерия: |
|||
2 |
|
|
~ |
|
|
|
|
n 1 D / D =((13-1)14,6)/12=14,6. |
|||||
набл |
|
|
0 |
|
|
|
|
По условию, конкурирующая гипотеза имеет вид D 12 , |
|||||
поэтому критическая область правосторонняя. |
||||||
|
По таблице, по уровню значимости 0,01 и числу степеней |
|||||
свободы |
k = n-1 = 13-1 = 12 |
находим критическую точку |
||||
|
|
|
|
|
|
|
2 |
0,01; |
12 =26,2. |
|
|
||
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
104 |
|
Так как набл2 кр2 - нет оснований отвергнуть нулевую гипотезу. Другими словами, различие между исправленной дисперсией (14,6) и гипотетической генеральной дисперсией (12) – незначимое.
Правило 2. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : D D0 о равенстве неизвестной генеральной дисперсии нормальной совокупности
гипотетическому |
значению |
при |
конкурирующей |
гипотезе |
||||||||||||
H1 : D D0 , надо вычислить наблюдаемое значение критерия |
||||||||||||||||
2 |
|
|
~ |
|
|
и по таблице критических точек распреде- |
||||||||||
|
n 1 D / D |
|
||||||||||||||
набл |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ления 2 найти левую критическую |
точку 2 1 / 2; k |
и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кр |
|
|
правую критическую точку 2 |
/ 2; k . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
кр |
|
|
|
|
|
|
|
|
Если 2 |
2 |
|
2 |
|
- нет оснований отвергнуть |
||||||||||
|
|
|
л ев.кр |
|
|
набл |
|
|
прав.кр |
|
|
|
|
|
|
|
нулевую гипотезу. |
|
Если |
2 |
|
|
2 |
|
или |
2 |
2 |
- |
|||||
|
|
|
|
|
|
|
|
набл |
|
л ев.кр |
|
набл |
прав.кр |
|
||
нулевую гипотезу отвергают. |
|
|
|
|
|
|
|
|
||||||||
|
Пример. 2.12. Из нормальной генеральной совокупности |
|||||||||||||||
извлечена выборка объема |
n 13 и по ней найдена исправлен- |
|||||||||||||||
ная выборочная дисперсия |
~ |
|
|
|
|
|
|
|
||||||||
D =10,3. Требуется при уровне зна- |
||||||||||||||||
чимости |
0,02 проверить |
нулевую |
гипотезу |
H0 : D D0 =12, |
||||||||||||
приняв в качестве конкурирующей гипотезы H1 : D 12 . |
|
|||||||||||||||
|
Решение. |
Найдем |
|
наблюденное значение |
критерия: |
|||||||||||
2 |
|
|
~ |
|
=((13-1)10,3)/12=10,3. |
|
|
|
|
|||||||
|
n 1 D / D |
|
|
|
|
|||||||||||
набл |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию конкурирующая гипотеза имеет вид D 12 , |
|||||||||||||||
поэтому критическая область двусторонняя. |
|
|
|
|||||||||||||
|
По |
таблице, |
|
находим |
критические |
точки: |
левую |
- |
||||||||
2 |
1 / 2; k = 2 |
|
1 0,02 / 2;12 = |
2 |
0,99;12 3,57 и пра- |
|||||||||||
кр |
|
|
|
кр |
|
|
|
|
|
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
105 |
|
|
|
|
|
|
|
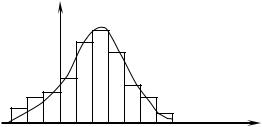
вую - кр2 / 2; k = кр2 0,01;12 26,2 . Так как наблюдавшееся
значение критерия принадлежит области принятия гипотезы (3,57<10,3<26,2) – нет оснований ее отвергнуть. Другими словами, исправленная выборочная дисперсия (10,3) незначимо отличается от гипотетической генеральной дисперсии (12).
Правило 3. При конкурирующей гипотезе H1 : D D0
находят критическую точку кр2 1 ; k .
Если набл2 кр2 1 ; k - нет оснований отвергнуть нулевую гипотезу.
Если набл2 кр2 1 ; k - нулевую гипотезу отвергают.
2.10. Выравнивание статистических рядов
При обработке статистического материала часто приходится решать вопрос о том, как подобрать для статистического ряда плавную теоретическую кривую распределения, выражающую лишь существенные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных (рис. 7). Такая задача называется задачей выравнивания (сглаживания) статистических рядов.
f(х)
х
0
Рис. 7106

Как правило, принципиальный вид теоретической кривой выбирается заранее, в соответствии с задачей, а в некоторых случаях с внешним видом статистического распределения. Аналитическое выражение выбранной кривой распределения зависит от некоторых параметров. Задача выравнивания статистического ряда переходит в задачу рационального выбора тех значений параметров, при которых соответствие между статистическим и теоретическим распределениями оказывается наилучшим. При сглаживании эмпирических зависимостей или при подборе параметров распределения применяют метод наименьших квадратов. Рассмотрим этот метод.
Пусть в результате опыта получен ряд экспериментальных точек и построен график зависимости y от x (рис. 8).
y
0 |
x |
|
|

полиномом степени n 1 , так, чтобы она в точности прошла
через каждую из точек (рис. 8). Однако такое решение вопроса обычно не является удовлетворительным, так как такое нерегулярное поведение экспериментальных точек связано не с объективным характером зависимости y от x, а исключительно с ошибками измерений. Желательно обработать экспериментальные данные так, чтобы по возможности точно отразить общую тенденцию зависимости y от x, но вместе с тем сгладить незакономерные случайные отклонения, связанные с неизбежными погрешностями самого наблюдения.
Для решения подобных задач обычно применяется расчетный метод, известный под названием «метода наименьших квадратов». Этот метод дает возможность при заданном типе зависимости y x (эмпирическая функция) так выбрать ее
числовые параметры, чтобы кривая y x наилучшим образом отражала экспериментальные данные.
Вопрос о выборе кривой решается либо непосредственно по внешнему виду экспериментальной зависимости, либо вид заранее известен из физических соображений. Требуется определить параметры этой зависимости.
Суть метода наименьших квадратов для определения параметров эмпирической зависимости y x сводится к то-
му, чтобы сумма квадратов отклонений экспериментальных точек от сглаживающей кривой ( y x ) обращалась в ми-
нимум.
Пусть имеется таблица экспериментальных данных и пусть выбран общий вид функции y x , зависящей от нескольких числовых параметров a,b, c,....Эти параметры необходимо выбрать согласно методу наименьших квадратов так, чтобы сумма квадратов отклонений yi от xi была мини-
108
|
n |
|
2 |
|
|
|
|
мальна, то есть если |
Si yi xi ; a, b, c , то |
||
|
i 1 |
|
|
|
S |
i |
|
|
|
0 |
|
|
a |
|
|
|
Si |
||
|
|
||
|
b |
0 |
|
|
|
||
|
Si |
|
|
|
0 |
||
|
c |
|
|
|
|
|
|
|
............ |
||
или
|
|
n |
yi |
xi |
|
|
|
|
|
|
|
|
|
|
|
|
; a, b, c,... |
|
0, |
|
|
||||||
|
|
i 1 |
|
|
|
|
|
a i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
yi |
xi |
|
|
|
|
0 |
|
|
|
|
|
|
|
; a, b, c,... |
|
|
, |
( 2.1 ) |
||||||
|
|
i 1 |
|
|
|
|
|
b i |
|
|
|
|
|
|
|
n |
y |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
i |
; a, b, c,... |
|
|
|
||||||
|
|
|
i |
|
|
|
|
|
|
|
|||
|
|
i 1 |
|
|
|
|
|
c i |
|
|
|
||
|
|
..................................................... |
|
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
- значение частной производной функции по па- |
|||||||||||
где |
|
||||||||||||
|
a i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, … - аналогично. Система |
|||||
раметру а в точке xi ; |
, |
|
|
||||||||||
|
|
|
|
|
b i |
|
c i |
|
|
|
|
|
|
(2.1) содержит столько же уравнений, сколько неизвестных a,b, c,....
В общем виде систему (2.1) решить нельзя, надо задаваться конкретным видом функции y x .
Рассмотрим наиболее часто встречающиеся виды зависимостей – линейную и квадратическую.
Пусть в опыте зарегистрирована совокупность значений
109
xi ; yi (i=1,2,…,n) (рис. 9)
y |
y=ax+b |
x1 x2 xn x
Рис. 9
Данную экспериментальную зависимость наилучшим образом отражает линейная функция
y ax b .
Подберем по методу наименьших квадратов параметры a
и b. Имеем y x; a,b ax b .
Дифференцируя это выражение по a и b, имеем:
x ;a
1;b
= xi ;a i
=1.
b i
Подставляя найденное в систему (2.1), получим два уравнения для определения a и b.
n yi axi b xi 0,
i1
n yi axi b 0.
i1
110
Раскрывая скобки и производя суммирование, имеем
n |
n |
n |
|
|
a xi2 |
b xi |
xi yi |
||
i 1 |
i 1 |
i 1 |
- |
|
n |
n |
|
|
|
a xi bn yi |
||||
|
||||
i 1 |
i 1 |
|
||
система для определения неизвестных параметров a и b.
Для определения параметров квадратичной зависимости y ax2 bx c соответственно получаем систему трех уравнений с тремя неизвестными
n |
|
axi2 bxi c xi2 |
|
|
|||
yi |
|
0 |
|||||
i 1 |
|
|
bxi c xi |
|
|
||
|
|
2 |
|
||||
|
|
|
|
||||
n |
|
axi |
|
|
|||
yi |
0 или |
||||||
i 1 |
|
axi2 bxi c |
|
|
|||
n |
|
|
|
||||
yi |
0 |
|
|||||
i 1 |
|
|
|
|
|
|
|
n |
|
n |
|
n |
|
|
|
a xi2 |
b xi |
cn yi |
|
||||
i 1 |
|
i 1 |
|
i 1 |
|
|
|
|
3 |
|
2 |
|
|
|
|
n |
n |
n |
|
n |
|
||
a xi |
b xi |
c xi |
|
xi yi . |
|||
i 1 |
|
i 1 |
|
i 1 |
|
i 1 |
|
n |
|
n |
|
n |
|
n |
|
a xi4 |
b xi3 |
c xi2 |
xi2 yi |
||||
i 1 |
|
i 1 |
|
i 1 |
i 1 |
|
|
Зная аналитический вид экспериментальной зависимости, можно определить значение функции в точках, не нашедших отражения в экспериментальной таблице, то есть сделать ка- кие-то прогнозы.
111
2.11. Критерии согласия
Пусть статистическое распределение выровнено с помощью некоторой теоретической кривой f(x) (рис. 8). Между теоретическим и статистическим распределениями неизбежны некоторые расхождения, как бы хорошо ни была подобрана кривая. Спрашивается: объясняются ли эти расхождения только лишь случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они существенны и связаны с тем, что данная кривая плохо выравнивает данное статистическое распределение. Таким образом, возникает вопрос, связанный с согласованием теоретического и статистического распределений, а именно вопрос проверки гипотез.
Для ответа на этот вопрос служат так называемые «критерии согласия».
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия: 2 («хиквадрат») К. Пирсона, Колмогорова, Смирнова и др.
Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый «критерий 2 » Пирсона. Кри-
терий не доказывает справедливость гипотезы - генеральная совокупность распределена по закону А, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.
Пусть произведено n независимых опытов, в каждом из которых величина Х приняла определенное значение. Результаты опытов сведены в k разрядов в виде статистического ряда:
112

Таблица 10
Ii |
x1;x2 |
x2;x3 |
. . . |
xi;xi+1 |
. . . |
xk;xk+1 |
|
|
|
|
|
|
|
pi* |
p1* |
p2* |
. . . |
pi* |
. . . |
pk* |
|
|
|
|
|
|
|
Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина Х имеет данный закон распределения (заданный функцией распределения F(x) или плотностью f(x)), который назовем «теоретическим».
Зная теоретический закон распределения, можно найти теоретические вероятности попадания случайной величины в каждый из разрядов: p1, p2, ..., pk.
Проверяя согласованность теоретического и статистического распределений, исходят из расхождений U между теоретическими вероятностями pi и наблюдаемыми частотами
pi nni (за счет чисто случайных причин). В качестве меры
расхождения между теоретическим и статистическим распределениями выбирается сумма квадратов отклонений (pi*- pi), взятая с некоторыми «весами» сi:
U k ci pi* pi 2 .
i 1
Коэффициенты сi вводят потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Одно и то же по абсолютной величине отклонение (pi*- pi) может быть мало значительным, если сама вероятность pi велика, и очень заметным, если она мала. Поэтому в качестве сi Пирсон предложил отношение
ci n , pi
113
тогда мера расхождения обозначается 2 :
|
k |
|
p* p |
2 |
|||
2 |
n |
|
i |
i |
. |
||
|
pi |
|
|||||
|
i 1 |
|
|
|
|||
Для удобства вычислений применяется формула |
|||||||
|
k |
n np |
|
2 |
|||
2 |
|
|
i |
i |
|
|
|
|
i 1 |
|
|
npi |
|
|
|
или |
|
|
|
|
|
|
|
2 |
k n |
n 2 |
( 2.2 ) |
||||
|
i |
i |
|
||||
|
i 1 |
|
|
ni |
|
|
|
где ni - эмпирические частоты, |
ni npi - теоретические час- |
||||||
тоты. |
|
|
|
|
|
|
|
Распределение 2 |
зависит от параметра k, называемого |
||||||
числом «степеней свободы» распределения. Число степеней свободы k равно числу разрядов r (число групп выборки или число вариант) минус число s независимых условий («связей»), наложенных на частоты pi* . Например, сумма всех частот равна единице, это требование (условие) накладывается во всех случаях; совпадение теоретических и статистических средних, дисперсий (накладываемые условия для нормального распределения) и так далее. Итак, если предполагаемое распределение нормальное, то число степеней свободы k r 3.
Для распределения 2 составлены специальные таблицы. Пользуясь ими можно для каждого значения 2 и числа степеней свободы k , найти вероятность того, что величина,
распределенная по закону |
2 , превзойдет это значение. |
Распределение 2 |
дает возможность оценить степень |
|
114 |
согласованности теоретического и статистического распределений. Пусть величина Х действительно распределена по закону F(x). Тогда вероятность р, определенная по таблице 4 приложения, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем фактически наблюдаемое
в данной серии опытов значение 2 . Если эта вероятность ма-
ла (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта следует считать противоречащим гипотезе Н о том, что закон распределения величины Х есть F(x). Эту гипотезу следует отбросить как неправдоподобную. Однако, если вероятность р сравнительно велика, можно признать расхождения между теоретическим и практическим распределениями несущественными и отнести их за счет случайных причин. Гипотезу Н о том, что величина Х распределена по закону F(x), можно считать правдоподобной или, по крайней мере, не противоречащей опытным данным.
Итак, схема применения критерия 2 к оценке согласованности теоретического и статистического распределений:
1.Определяется мера расхождения 2 по формуле (2.2).
2.Определяется число степеней свободы k, как число разрядов r минус число наложенных связей s:
k= r - s.
3.По k и 2 с помощью таблицы определяется вероят-
ность того, что величина, имеющая распределение 2 превзойдет данное значение 2 .
Если эта вероятность весьма мала, то гипотеза отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, гипотезу можно признать не противоречащей опытным данным. На практике, если р оказывается меньшим, чем 0,1, рекомендуется проверить эксперимент, если возможно
115
– повторить его и в случае, если заметные расхождения появятся снова, пытаться искать более подходящий для описания статистических данных закон распределения.
Подчеркнем, что с помощью любого критерия согласия можно только в некоторых случаях опровергнуть выбранную гипотезу Н и отбросить ее как явно несогласную с опытными данными. Если же вероятность р велика, то этот факт сам по себе не считается доказательством справедливости гипотезы Н, а указывает только на то, что гипотеза не противоречит опытным данным.
Для проверки нулевой гипотезы: генеральная совокупность распределена нормально, используют следующее пра-
вило. Обозначим значение критерия, вычисленное по данным наблюдений, через набл2 .
Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия
|
|
|
|
набл2 |
r |
n |
n 2 |
|
|
|
|
|
|
|
i |
ni |
i |
(2.3) |
|
|
|
|
|
|
i 1 |
|
|
|
|
и по таблице критических точек распределения 2 , |
по задан- |
||||||||
ному уровню |
значимости |
|
и |
числу степеней |
свободы |
||||
k r 3 |
найти |
критическую |
точку |
2 ; k , |
|||||
P 2 2 |
; k . |
|
|
|
|
кр |
|||
|
|
|
|
|
|||||
|
кр |
|
|
|
|
|
|
|
|
Если |
2 |
|
< |
2 |
- нет оснований отвергнуть нулевую |
||||
|
набл |
|
кр |
|
|
|
|
|
|
гипотезу.
Если набл2 > кр2 - нулевую гипотезу отвергают.
116
Для контроля вычислений формулу (2.3) преобразуют к
виду
набл2 |
|
r |
n2 |
|
|
|
|
|
i |
|
n . |
(2.4) |
|
|
||||||
|
i 1 ni |
|
|
|
||
|
|
|
|
|
|
|
Пример. 2.13. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
|
Эмп. частоты….. .6 |
13 |
38 |
74 |
106 |
85 |
30 |
14 |
|||||||||||
|
Теорет. частоты…3 14 42 82 99 |
|
76 |
37 |
13 |
||||||||||||||
|
Решение. Вычислим 2 |
|
, для чего составим расчетную |
||||||||||||||||
|
|
|
|
|
|
|
набл |
|
|
|
|
|
|
|
|
|
|
|
|
таблицу 11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 11 |
||
1 |
|
2 |
|
3 |
4 |
|
5 |
|
|
|
|
6 |
|
|
|
7 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i |
|
ni |
|
ni |
ni - |
|
( ni - ni ) |
( n |
i |
- n ) 2 |
/ |
|
n 2 |
|
n 2 / |
||||
|
|
|
|
|
ni |
|
|
|
|
|
|
i |
|
|
|
i |
|
i |
|
|
|
|
|
|
|
2 |
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
|
3 |
3 |
|
9 |
|
|
3 |
|
|
|
|
|
36 |
|
12 |
|
2 |
|
13 |
|
14 |
-1 |
|
1 |
|
|
0,07 |
|
|
|
169 |
|
12,07 |
|||
3 |
|
38 |
|
42 |
-4 |
|
16 |
|
|
0,38 |
|
|
|
1444 |
|
34,38 |
|||
4 |
|
74 |
|
82 |
-8 |
|
64 |
|
|
0,78 |
|
|
|
5476 |
|
66,78 |
|||
5 |
|
106 |
|
99 |
7 |
|
49 |
|
|
0,49 |
|
|
|
11236 |
|
113,49 |
|||
6 |
|
85 |
|
76 |
9 |
|
81 |
|
|
1,07 |
|
|
|
7225 |
|
95,07 |
|||
7 |
|
30 |
|
37 |
-7 |
|
49 |
|
|
1,32 |
|
|
|
900 |
|
24,32 |
|||
8 |
|
14 |
|
13 |
1 |
|
1 |
|
|
0,08 |
|
|
|
196 |
|
15,08 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
366 |
|
366 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
373,19 |
|
|
|
|
|
|
|
|
|
|
набл |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
=7,19 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
117 |
|
|
|
|
|
|
|
|
|
|
|
Контроль: набл2 =7,19 (по формуле (2.4)). Вычисления произведены правильно.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) r = 8, k = 8 – 3 = 5.
По таблице критических точек распределения 2 , по уровню значимости 0,05 и числу степеней свободы k = 5
находим 2 |
0,05;5 |
11,1. |
||
кр |
|
|
|
|
Так как 2 |
< |
2 |
- нет оснований отвергнуть нулевую |
|
|
набл |
|
кр |
|
гипотезу. Другими словами расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
2.12. Методика вычисления теоретических частот нормального распределения
Как было сказано выше, сущность критерия согласия Пирсона состоит в сравнении эмпирических и теоретических частот. Эмпирические частоты находят из опыта. Возникает вопрос о том, как найти теоретические частоты, если предполагается, что генеральная совокупность распределена нормально? Приведем один из способов решения этой задачи.
1. Весь интервал наблюдаемых значений X (выборки объема n) делят на s частичных интервалов xi , xi 1 одинаковой
длины. |
|
Находят |
середины |
частичных |
интервалов |
||||
x* x |
i |
x |
/ 2 ; в качестве частоты n |
i |
варианты |
x* |
прини- |
||
i |
i 1 |
|
|
|
|
i |
|
||
мают число вариант, которые попали в i-й интервал. В итоге получают последовательность равноотстоящих вариант и соответствующих им частот:
118
x* |
x* |
… |
x* |
1 |
2 |
|
s |
n1 |
n2 |
… |
ns . |
При этом ni n .
2. Вычисляют выборочную среднюю x * и выборочное
среднее квадратическое отклонение * , например, методом произведений.
причем наименьшее значение Z, то есть z1 полагают равным
3. Нормируют случайную величину X, то есть переходят |
||||||||
к величине Z X x* / * |
и вычисляют концы интервалов |
|||||||
zi , zi1 : |
|
|
|
|
|
|
|
|
z |
i |
x x* / * , |
z |
i1 |
x |
i1 |
x* / * , |
|
|
i |
|
|
|
|
|||
, а наибольшее, то есть zs , полагают равным |
. |
|||||||
4. Вычисляют теоретические вероятности pi |
попадания |
|||||||
X в интервалы xi , xi1 по равенству |
pi Ф zi1 |
Ф zi ( |
||||||
Ф z - функция Лапласа) и находят искомые теоретические частоты ni npi .
Пример. 2.14. Найти теоретические частоты по заданному интервальному распределению выборки объема n 200 , предполагая, что генеральная совокупность распределена нормально (табл. 12).
Решение. |
|
|
|
|
|
|
1. Найдем середины интервалов |
x* x |
i |
x |
i 1 |
/ 2 |
. Полу- |
|
i |
|
|
|
чим последовательность равноотстоящих вариант xi* и соответствующих им частот ni :
119

xi* |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
ni |
15 |
26 |
25 |
30 |
26 |
21 |
24 |
20 |
13 |
2.Пользуясь методом произведений, найдем выборочную среднюю и выборочное среднее квадратическое отклонение:
x* 12,63, * 4,695 .
3.Найдем интервалы zi , zi1 , учитывая, что x* 12,63,
* 4,695 , 1/ * 0,213 , составив расчетную таблицу 12.
4.Найдем теоретические вероятности pi и искомые теоретические частоты ni npi для чего составим расчетные таб-
лицы 13,14.
Таблица 12
Номер |
Границы |
Часто- |
Номер |
Границы |
Часто- |
|||
интерва- |
интер- |
та |
интерва- |
интерва- |
та |
|||
ла |
вала |
|
|
ла |
ла |
|
|
|
i |
xi |
|
x i 1 |
ni |
i |
xi |
x i 1 |
ni |
|
|
|
|
|
|
|
|
|
1 |
4 |
|
6 |
15 |
6 |
14 |
16 |
21 |
2 |
6 |
|
8 |
26 |
7 |
16 |
18 |
24 |
3 |
8 |
|
10 |
25 |
8 |
18 |
20 |
20 |
4 |
10 |
|
12 |
30 |
9 |
20 |
22 |
13 |
5 |
12 |
|
14 |
26 |
|
|
|
n 200 |
|
|
|
|
|
|
|
|
|
120
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 13 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
Границы |
||||
|
интервала |
xi |
|
* |
xi 1 |
|
* |
|
|
интервала |
|||||
|
x |
x |
|||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
xi 1 |
|
|
|
|
|
|
zi |
|
zi 1 |
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
xi |
|
* / * |
|
xi 1 |
|
* / * |
|
|
|
|
|
|
|
|
|
x |
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
4 |
6 |
- |
|
|
-6,63 |
|
|
- |
|
-1,41 |
||||
2 |
6 |
8 |
-6,63 |
-4,63 |
-1,41 |
|
-0,99 |
||||||||
3 |
8 |
10 |
-4,63 |
-2,63 |
-0,99 |
|
-0,56 |
||||||||
4 |
10 |
12 |
-2,63 |
-0,63 |
-0,156 |
|
-0,13 |
||||||||
5 |
12 |
14 |
-0,63 |
1,37 |
|
-0,13 |
|
0,29 |
|||||||
6 |
14 |
16 |
1,37 |
3,37 |
|
0,29 |
|
0,72 |
|||||||
7 |
16 |
18 |
3,37 |
5,37 |
|
0,72 |
|
1,14 |
|||||||
8 |
18 |
20 |
5,37 |
7,37 |
|
1,14 |
|
1,57 |
|||||||
9 |
20 |
22 |
7,37 |
- |
|
|
1,57 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
121
|
|
|
|
|
|
|
|
|
|
|
Таблица 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Границы |
|
|
|
|
|
|
|
|
|
|
|
|
интервала |
Ф zi |
Ф zi 1 |
p |
i |
= Ф z |
i 1 |
- |
n np =200 |
|
||
|
|
|
|
|
|
|
|
i |
i |
|
||
|
|
|
|
|
|
|
- Ф zi |
|
|
pi |
|
|
i |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zi |
zi 1 |
|
|
|
|
|
|
|
|
|
|
1 |
- |
- |
-0,5 |
- |
|
|
0,0793 |
|
|
15,86 |
|
|
2 |
-1,41 |
1,41 |
- |
0,4207 |
|
|
0,0818 |
|
|
16,36 |
|
|
|
|
|
|
|
|
|
||||||
3 |
-0,99 |
- |
0,4207 |
- |
|
|
0,1266 |
|
|
25,32 |
|
|
0,99 |
|
0,3389 |
|
|
|
|
|
|||||
|
|
- |
|
|
|
|
|
|
|
|
||
4 |
-0,56 |
|
|
|
|
0,1606 |
|
|
32,12 |
|
||
- |
0,3389 |
- |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
5 |
-0,13 |
0,56 |
- |
0,2123 |
|
|
0,1658 |
|
|
33,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0,29 |
- |
0,2123 |
- |
|
|
0,1501 |
|
|
30,02 |
|
|
7 |
0,72 |
0,13 |
- |
0,0517 |
|
|
1,1087 |
|
|
21,74 |
|
|
|
|
|
|
|
|
|
||||||
8 |
1,14 |
0,29 |
0,0517 |
0,1141 |
|
|
0,0689 |
|
|
13,78 |
|
|
|
|
|
|
|
|
|
|
|||||
9 |
1,57 |
0,72 |
0,1141 |
0,2642 |
|
|
0,0582 |
|
|
11,64 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1,14 |
0,2642 |
0,3729 |
|
|
|
|
|
|
|
|
|
|
1,57 |
0,3729 |
0,4418 |
|
|
|
|
|
|
|
|
|
|
|
0,4418 |
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi 1 |
|
|
ni 200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искомые теоретические частоты помещены в последнем столбце таблицы 14.
122

2.13.Система двух случайных величин
2.13.1.Понятие о системе нескольких случайных величин
До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости, — дискретная одномерная величина; расстояние от орудия до места падения снаряда — непрерывная одномерная случайная величина.
Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя,. .., п числами. Такие величины называются естественно двумерными, трехмерными, . . ., n-мерными.
Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично п -мерную величину можно рассматривать как систему п случайных величин. Например, трехмерная величина (X, Y, Z) определяет систему случайных величин X, Y и Z. Например, станок-автомат штампует стальные плитки. Если контролируемыми размерами являются длина X и ширина Y, то имеем двумерную случайную величину (X, Y); если же контролируется и высота Z, то имеем трехмерную величину (X, Y, Z).
Двумерную случайную величину (X, Y) геометрически можно истолковать либо как случайную точку М (X, Y) на плоскости (как точку со случайными координатами), либо
как случайный вектор OM . Трехмерную случайную величину геометрически можно истолковать как точку М (Х, Y, Z) в
трехмерном пространстве или как вектор OM . Целесообразно различать дискретные (составляющие
этих величин дискретны) и непрерывные (составляющие этих величин непрерывны) многомерные случайные величины.
123
2.13.2. Закон распределения вероятностей дискретной двумерной случайной величины
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, то есть пар чисел xi , yi и их вероятностей р xi , yi
(i = 1, 2, . . . . п; j = 1, 2, . . . . т). Обычно закон распределения задают в виде таблицы с двойным входом (табл. 15).
Первая строка таблицы содержит все возможные значения составляющей X, а первый столбец — все возможные значе-
ния |
составляющей Y. В |
клетке, стоящей на пересечении |
|
«столбца |
xi » и «строки |
y j », указана вероятность р xi , yi |
|
того, |
что |
двумерная случайная величина примет значение |
|
xi , yi . |
|
|
|
|
Так как события X xi ,Y y j i 1, , n; j 1, , m |
||
образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы, равна единице.
|
|
|
|
|
|
Таблица 15 |
|
|
|
|
X |
|
|
Y |
x1 |
x2 |
|
xi |
|
xn |
|
|
|
|
|
|
|
y1 |
р x1, y1 |
р x2 , y1 |
|
р xi , y1 |
|
р xn , y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y j |
р x1, y j |
р x2 , y j |
|
р xi , y j |
|
р xn , y j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ym |
р x1, ym |
р x2 , ym |
|
р xi , ym |
|
р xn , ym |
|
|
|
|
|
|
|
|
|
|
124 |
|
|
|
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой
из составляющих. Действительно, |
например, события |
X x1,Y y1 , X x1,Y y2 , …, |
X x1,Y ym несо- |
вместны, поэтому вероятность Р x1 |
того, что X примет |
значение xi , по теореме сложения такова:
Рx1 = р x1, y1 + р x1, y2 +…+ р x1, ym .
Вобщем случае, для того, чтобы найти вероятность РX xi , надо просуммировать вероятности столбца xi . Ана-
логично сложив вероятности «строки y j », получим вероят-
ность Р Y y j .
Вероятность события, состоящего в том, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y, обозначим через F x; y . Если x и y будут изменяться,
то будет изменяться и F x; y , то есть F x; y - функция от
x и y.
Функцией распределения двумерной случайной величины X ;Y называют функцию F x; y , определяющую для
каждой пары чисел x и y вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y:
F x; y P X x,Y y .
Геометрически это равенство можно истолковать так: F x; y есть вероятность того, что случайная точка X ;Y попадет в бесконечный квадрант с вершиной x; y , расположенный левее и ниже этой вершины (рис. 10).
125

Y x; y
X
Рис. 10
Свойства функции распределения двумерной случайной величины
1.Значения функции распределения удовлетворяют двойному неравенству 0 F x; y 1.
2.F x; y есть неубывающая функция по каждо-
му |
аргументу |
F x 2 ; y F x1 ; y , |
если |
x2 x1 ; |
F x; y2 F x; y1 , если y2 y1 ; |
|
|
||
3.Имеют место предельные соотношения:
1)F ; y 0 ; 2) F x; 0 ; 3) F ; 0 ;
4) |
F ; 1. |
|
|
|
|
4. |
а) При y= функция распределения системы |
ста- |
|
новится |
функцией распределения |
составляющей |
X: |
|
F |
x; F1 x . |
|
|
|
|
б) При x= функция распределения становится функ- |
|||
цией распределения составляющей Y: |
F ; y F2 y . |
|
||
2.13.3.Вероятность попадания случайной точки
вполуполосу
Используя функцию распределения системы случайных величин X и Y , легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу
x1 X x2 и Y y или в полуполосу X x и y1 Y y2 (рис. 11). Вычитая из вероятности попадания случайной точки
126

|
в квадрант с вершиной x2 ; y |
||||
|
вероятность попадания точки в |
||||
|
квадрант с вершиной |
x1; y , |
|||
|
получим |
|
|
|
|
|
P x1 X x2 ,Y y |
. |
|||
|
F x2 , y F x1, y |
||||
|
|
||||
|
Аналогично, |
|
|
|
|
|
P X x, y1 Y y2 |
|
. |
|
|
|
F x, y2 F x, y1 |
|
|
|
|
|
|
|
|
|
|
Рис. 11 |
Таким образом, вероят- |
||||
|
|||||
|
ность попадания |
случайной |
|||
точки в полуполосу равна приращению функции распределения по одному из аргументов.
2.13.4. Вероятность попадания случайной точки в прямоугольник
Рассмотрим прямоугольник ABCD со сторонами, параллельными координатным осям (рис. 12). Пусть уравнения сторон таковы: X x1, X x2 ,Y y1,Y y2 . Найдем вероятность попадания случайной точки X ;Y в этот прямо-
угольник. Искомую вероятность можно найти как разность вероятности попадания случайной точки в полуполосу АВ ( F x2 , y2 F x1, y2 ) и вероятности попадания точки в по-
луполосу CD ( F x2 , y1 F x1, y1 ) :
P x1 X x2 , y1 Y y2 F x2 , y2 F x1, y2F x2 , y1 F x1, y1 .
127

Y |
A x1; y2 |
|
|
B x2 ; y2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 С x ; |
y |
|
|
|
|
|
D |
x |
|
; y |
|
||
|
|||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
2 |
1 |
|
|
x1 |
|
|
|
|
|
|
|
x2 |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12
2.13.5. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)
Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения.
Плотностью совместного распределения вероятностей f x; y двумерной непрерывной случайной величины X ;Y
называют вторую смешанную частную производную от функции распределения
f x; y 2 F x; y .x y
Геометрически этой функции соответствует поверх-
ность, которую называют поверхностью распределения.
Функцию f x; y можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (со сторонами x и y ) к площади этого прямо-
угольника, когда обе стороны прямоугольника стремятся к нулю.
128
Зная плотность совместного распределения f x; y , можно найти функцию распределения F x; y по формуле
y x
F x; y f x; y dxdy ,
что следует из определения плотности распределения двумерной непрерывной случайной величины X ;Y .
Тогда вероятность попадания случайной точки X ;Y в
область D
P X ;Y D f x; y dxdy .
D
Геометрически это равенство можно истолковать так: вероятность попадания точки X ;Y в область D равна объему тела, ограниченного сверху поверхностью z f x; y , основанием которого служит проекция этой поверхности на плоскость xOy .
Свойства двумерной плотности вероятности
1. Двумерная плотность вероятности неотрицательна:
fx; y 0 .
2.Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
f x; y dxdy 1.
Плотность распределения одной из составляющих равна несобственному интегралу с бесконечными пределами от плотности совместного распределения системы, причем переменная интегрирования соответствует другой составляющей
f1 x f x; y dy ;
f2 y |
|
x; y dx . |
f |
||
|
|
|
|
129 |
|
2.13.6.Условные законы распределения составляющих системы дискретных случайных величин
Пусть X ;Y - непрерывная случайная величина. Условной плотностью x / y распределения состав-
ляющих X при данном значении Y=y называют отношение f x; y системы X ;Y к плот-
ности распределения f2 y составляющей Y:
x / y f x; y / f2 y .
Отличие условной плотности x / y от безусловной f1 x состоит в том, что условная плотность дает распределение X при условии, что составляющая Y приняла значение Y=y; функция f1 x дает распределение X независимо от то-
го, какие из возможных значений приняла составляющая Y. Аналогично, для условной плотности составляющей Y
при данном значении X=x.
Отсюда: закон распределения системы случайных ве-
личин |
y x / y или f x; y = f1 x y / x . |
|
f x; y = f2 |
||
Условные плотности распределения обладают свойст- |
||
вами: |
|
|
|
x / y 0 , |
|
|
x / y dx 1; |
|
|
|
|
|
y / x 0 , |
|
|
y / x dx 1 . |
|
2.13.7. Условное математическое ожидание
Условным математическим ожиданием дискретной случайной величины Y при X=x называют произведение возможных значений Y на их условные вероятности:
130
|
M Y / X x |
m |
|
|
|
y j p y j / x . |
( 2.5 ) |
||
|
|
j 1 |
|
|
Для непрерывных величин |
|
|
||
|
M Y / X x |
|
y / x dy , |
|
|
y |
|
||
где y / x - |
|
|
|
|
условная плотность случайной величины Y |
||||
при X=x. |
|
|
|
M Y / x есть |
Условное |
математическое ожидание |
|||
функция от x:
M Y / x = f x ,
которую называют функцией регрессии Y на X.
Аналогично определяется условное математическое ожидание случайной величины X и функция регрессии X
наY:
M X / y = y .
Пример. 2.15. Дискретная двумерная случайная величина задана таблицей
|
|
|
|
|
|
Таблица 16 |
||
|
|
|
|
|
X |
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
x1 =1 |
|
x2 =3 |
x3 =4 |
x4 =8 |
|
|
y1 =3 |
|
0,15 |
|
0,06 |
0,25 |
0,04 |
|
|
y2 =6 |
|
0,30 |
|
0,10 |
0,03 |
0,07 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти условное математическое ожидание состав- |
||||||||
ляющей Y при X= x1 1. |
p x1 , |
|
|
|
||||
Решение. |
Найдем |
для чего сложим вероятно- |
||||||
сти, помещенные в первом столбце таблицы:
131
p x1 =0,15+0,30=0,45.
Найдем условное распределение вероятностей величины Y при X= x1 1:
p y1 / x1 p x1, y1 / p x1 0,15 / 0,45 1/ 3; p y2 / x1 p x1, y2 / p x1 0,30 / 0,45 2 / 3;
Найдем искомое условное математическое ожидание по формуле (2.5):
2
M Y / X x1 y j p y j / x y1 p y1 / x1 y2 p y2 / x1
j1
=3(1/3)+6(2/3)=5.
Две случайные величины независимы, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого следует, что условные распределения независимых величин равны их безусловным распределениям.
Теорема. Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения системы X ;Y была равна произ-
ведению функций распределения составляющих:
F x; y F1 x F2 y .
Следствие. Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность совместного распределения системы X ;Y была равна произведению плотностей распределения состав-
ляющих:
f x; y = f1 x f2 y .
2.13.8. Числовые характеристики системы двух случайных величин. Корреляционный момент.
Коэффициент корреляции
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих ис-
132
пользуют и другие характеристики: корреляционный мо-
мент и коэффициент корреляции.
Корреляционным моментом xy случайных величин
X и Y называют математическое ожидание произведения
отклонений этих величин:
xy M X M X Y M Y .
Для вычисления корреляционного момента дискретных величин используют формулу
|
n |
m |
xy xi M X y j M Y p xi , y j , |
||
|
i 1 j 1 |
|
а для непрерывных величин – формулу |
||
|
|
|
xy |
|
x M X y M Y f x; y dxdy . |
|
|
|
Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент равен нулю, если X и Y независимы. Если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y, то есть величина корреляционного момента зависит от единиц измерения случайных величин. Поэтому для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины. Такая особенность корреляционного момента является недостатком этой числовой характеристики и чтобы устранить этот недостаток, вводят новую числовую характери-
стику – коэффициент корреляции.
Коэффициентом корреляции rxy случайных величин X
и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
133

r xy xy / x y .
Коэффициентом корреляции безразмерная величина, то есть не зависит от выбора единиц измерения случайных величин. В этом преимущество коэффициента корреляции перед корреляционным моментом. Коэффициент корреля-
ции независимых случайных величин равен нулю.
Теорема. Абсолютная величина коэффициента корреляции не превышает единицы: r xy 1.
Две случайные величины X и Y называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля. X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Если коэффициент корреляции величин X и Y равен 1 , то X и Y связаны линейной зависимостью, то есть коэффициент корреляции измеряет силу (тесноту) линейной связи между X и Y.
Две коррелированные величины также и зависимы. Однако обратное утверждение не всегда имеет место, то есть если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, а может и равняться нулю.
Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Из некоррелированности нормально распределенных величин вытекает их независимость. Для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.
134
2.13.9. Линейная регрессия. Прямые линии среднеквадратической регрессии
Рассмотрим двумерную случайную величину X ;Y ,
где X и Y – зависимые случайные величины. Представим одну из величин как функцию другой. А именно, опишем приближенно величину Y в виде линейной функции величины X (точное приближение невозможно):
Y g x X ,
где и - параметры, которые определяем с помощью метода наименьших квадратов.
Функцию g x X называют «наилучшим приближением» Y по методу наименьших квадратов, если математическое ожидание M Y g X 2 принимает наименьшее возможное значение; функцию g x называют средне-
квадратической регрессией Y на X.
Теорема. Линейная средняя квадратическая регрессия Y на X имеет вид
g X m |
|
r |
y |
X m |
|
, |
|
|
||||
y |
|
|
|
|
||||||||
|
|
|
|
x |
|
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
где mx M X , |
my M Y , x |
|
|
|
, |
|||||||
D X |
, y |
D Y |
||||||||||
r xy / x y - коэффициент корреляции величин X и Y. |
||||||||||||
Коэффициент |
r |
y |
|
называют |
коэффициентом |
|||||||
x |
||||||||||||
регрессии Y на X, а прямую
ymy r y X mx
x
называют прямой среднеквадратической регрессии Y на X. Величину y2 1 r2 называют остаточной дисперсией
случайной величины Y относительно случайной величины X
135

.Она характеризует величину ошибки, которую допускают при замене Y линейной функцией g x X . При r= 1
остаточная дисперсия равна нулю, то есть Y и X связаны линейной функциональной зависимостью.
Аналогично, прямая среднеквадратической регрессии
X на Y
x mx r x Y my .y
Если r= 1, то обе прямые регрессии совпадают.
Обе прямые регрессии проходят через точку mx ; my ,
которую называют центром совместного распределения величин X и Y.
Если обе функции регрессии Y на X и X на Y линейны, то говорят, что X и Y связаны линейной корреляцион-
ной зависимостью.
Теорема. Если двумерная случайная величина X ;Y
распределена нормально, то X и Y связаны линейной корреляционной зависимостью.
Уравнения прямых регрессии совпадают с уравнениями прямых среднеквадратической регрессии
y a2 r y x a1
x
x a1 r x y a2 .
y
2.14. Элементы теории корреляции
Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Рассмотрим зависимость Y от одной случайной (или не случайной) величины X.
136
Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.
Строго функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, при чем среди них могут быть и общие для обеих величин (под «общими» подразумеваются такие факторы, которые воздействуют и на X и на
Y). В этом случае возникает статистическая зависимость.
Например, если Y зависит от случайных факторов Z1, Z2 ,V1,V2 , а X зависит от случайных факторов Z1, Z2 ,U1 то между X и Y имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: Z1, Z2
.
Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статисти-
ческую зависимость называют корреляционной.
Например, пусть Y – урожай зерна, X – количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, то есть Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, то есть Y связан с X корреляционной зависимостью.
137
2.14.1. Отыскание параметров выборочного уравнения прямой линии среднеквадратической регрессии
по несгруппированным данным
Пусть изучается система количественных признаков
(X,Y). В результате n независимых опытов получены n пар чи- |
||
сел |
x1, y1 , x2 , y2 , , xn , yn . Будем искать |
выборочное |
уравнение прямой линии регрессии Y на X в виде |
|
|
|
Y yx x b , |
( 2.6 ) |
где yx - выборочный коэффициент регрессии Y на X, он является оценкой коэффициента регрессии .
Параметры yx и b подбираются так, чтобы точки, по-
строенные по данным наблюдений, на плоскости xOy лежали как можно ближе к прямой (2.6). Применяя рассмотренный ранее метод наименьших квадратов, получим систему двух линейных уравнений относительно yx и b :
|
2 |
xy x b xy; |
|
||
x |
|
|
|
|
. |
x nb y
xy
Решив эту систему, найдем искомые параметры:
|
|
|
2 |
|
2 |
; |
|
yx n xy x y / n x |
|
x |
. |
||||
|
2 |
|
|
2 |
|
2 |
|
|
y x xy / n x |
|
|
||||
b x |
|
|
x |
||||
( 2.7 )
( 2.8 )
Пример. 2.16. Найти выборочное уравнение прямой линии регрессии Y на X по данным n=5 наблюдений:
x |
1,00 |
1,50 |
3,00 |
4,50 |
5,00 |
y |
1,25 |
1,40 |
1,50 |
1,75 |
2,25 |
|
|
|
|
138 |
|
Решение. Составим расчетную таблицу
|
|
|
|
|
|
Таблица 17 |
|
|
|
|
|
|
|
|
|
xi |
|
yi |
|
x 2 |
|
xi yi |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
1,00 |
|
1,25 |
|
1,00 |
|
1,250 |
|
1,50 |
|
1,40 |
|
2,25 |
|
2,100 |
|
3,00 |
|
1,50 |
|
9,00 |
|
4,500 |
|
4,50 |
|
1,75 |
|
20,25 |
|
7,875 |
|
5,00 |
|
2,25 |
|
25,00 |
|
11,250 |
|
|
|
|
|
|
|
|
|
xi |
15 |
yi |
8,15 |
x2 |
57,50 |
xi yi |
26,975 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
Найдем искомые параметры, для чего подставим вычисленные по таблице суммы в соотношения (2.8):
yx 5 26,975 15 8,15 / 5 57,5 152 0,202; b 57,5 8,15 15 26,975 / 62,5 1,024.
Тогда искомое уравнение регрессии:
Y 0,202x 1,024 .
Чтобы получить представление, насколько хорошо вычисленные по этому уравнению значения Yi согласуются с на-
блюдаемыми значениями, найдем отклонения Yi - yi . Результаты вычислений приведены в таблице 18.
139
|
|
|
Таблица 18 |
|
|
|
|
|
|
xi |
Y i |
yi |
|
Yi - yi |
|
|
|
|
|
1,00 |
1,226 |
1,25 |
|
-0,024 |
1,50 |
1,327 |
1,40 |
|
-0,073 |
3,00 |
1,630 |
1,50 |
|
0,130 |
4,50 |
1,933 |
1,75 |
|
0,183 |
5,00 |
2,034 |
2,25 |
|
-0,216 |
|
|
|
|
|
Как видно, не все отклонения достаточно малы. Это объясняется малым числом наблюдений.
2.14.2. Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным.
Проверка гипотезы о значимости выборочного коэффициента корреляции. Методика вычисления выборочного коэффициента корреляции
При большом числе наблюдений одно и то же значение x может встретиться nx раз, одно и то же значение y - n y раз,
одна и та же пара чисел x; y может наблюдаться nxy раз. По-
этому данные наблюдений группируют, то есть подсчитывают частоты nx , n y , nxy . Все сгруппированные данные записыва-
ют в виде таблицы, которую называют корреляционной.
Поскольку данные наблюдений сгруппированы в виде корреляционной таблицы, то для определения параметров уравнения прямой линии регрессии Y на X, полученную систему уравнений (2.7) необходимо записать так, чтобы она отражала данные корреляционной таблицы.
140

Воспользовавшись тождествами:
x nx; |
x2 nx 2 ; |
y ny; |
xy nxy xy |
и системой уравнений (2.7) , найдем параметры yx и b , и искомое уравнение yx xy x b .
Однако, целесообразнее, введя новую величину - выборочный коэффициент корреляции и проведя некоторые преобразования, записать выборочное уравнение прямой линии регрессии Y на X
yx y rв ~y x x .
x~
Здесь |
rв - выборочный |
коэффициент |
корреляции, который |
|
определяется равенством |
|
|
|
|
|
rв |
|
nxy xy nxy |
, |
|
|
|
||
|
~ ~ |
|||
|
|
|
n x y |
|
где x,y |
- варианты (наблюдавшиеся значения) признаков X и |
|||
Y; nxy |
- частота пары вариант x; y ; n – объем выборки (сум- |
|||
ма всех частот); ~ , ~ - выборочные средние квадратическиеx y
отклонения; x, y - выборочные средние.
Выборочный коэффициент корреляции rв является оцен-
кой коэффициента корреляции r генеральной совокупности и поэтому также служит для измерения линейной связи между величинами – количественными признаками Y и X . ПустьX ;Y распределена
нормально. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции генераль-
141

ной совокупности также отличен от нуля. Возникает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или о равенстве нулю коэффициента корреляции генеральной совокупности). Если гипотеза о равенстве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции значим, а величины X и Y коррелированны, то есть, связаны линейной зависимостью; если гипотеза принята, то выборочный коэффициент корреляции незначим, а величины X и Y не коррелированны, то есть, не связаны линейной зависимостью.
При заданном уровне значимости проверим нулевую гипотезу H0 : rГ 0 о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
H1 : rГ 0.
Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : rГ 0 о равен-
стве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 : rГ 0 , надо вычислить наблюдаемое зна-
чение критерия |
Т |
набл |
r |
n 2 / |
1 r 2 |
и по таблице крити- |
|
|
в |
|
в |
|
ческих точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы k n 2 найти критическую точку tкр ; k для двусторонней критической области.
Если Tнабл tкр - нет оснований отвергнуть нулевую гипотезу.
Если Tнабл tкр - нулевую гипотезу отвергают.
Пример. 2.17. По выборке объема n=122, извлеченной из нормальной двумерной совокупности, найден выборочный коэффициент корреляции rв =0,4. При уровне значимости 0,05
142

проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе
H1 : rГ 0.
Решение. Найдем наблюдаемое значение критерия:
Т набл rв 
 n 2 /
n 2 / 
 1 rв2 0,4
1 rв2 0,4
 122 2 /
122 2 / 
 1 0,42 4,78 .
1 0,42 4,78 .
По условию, конкурирующая гипотеза имеет вид rГ 0 , поэтому критическая область – двусторонняя.
По уровню значимости 0,05 и числу степеней свободы k 122 2 120 находим по таблице приложения для двусторонней критической области критическую точку tкр 0,05;120 1,98.
Поскольку Tнабл нулевую гипотезу отвергаем. Дру-
гими словами, выборочный коэффициент корреляции значимо отличается от нуля, то есть X и Y коррелированны.
Рассмотрим теперь, как по данным корреляционной таблицы вычислить выборочный коэффициент корреляции и записать выборочное уравнение прямой линии регрессии.
|
Для упрощения расчета переходят к условным вариан- |
||
там (при этом величина |
rв не меняется) ui xi C1 / h1 и |
||
v j |
y j C2 |
/ h2 , где C1 |
и C2 - ложные нули для вариант x и |
y, h1 |
и h2 - |
шаги, равные разности между двумя соседними |
|
вариантами. В этом случае выборочный коэффициент корре-
|
|
|
|
|
|
|
|
|
n |
uv n |
|
v |
|
ляции |
вычисляется по формуле |
|
rв |
u |
. Тогда |
||||||||
|
|
uv~ ~ |
|||||||||||
~ |
~ |
|
|
|
|
|
|
|
|
n u v |
|
||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
||
x uh1 c1 |
, |
y vh2 c2 . |
|
||||||||||
x h1 u , y h2 v , |
|
||||||||||||
143

Пример. 2.18. По данным корреляционной таблицы найти выборочное уравнение прямой линии регрессии Y на X.
|
|
|
|
|
|
|
|
Таблица 19 |
|
|
|
|
|
|
|
|
|
Y |
|
|
|
X |
|
|
n y |
|
|
10 |
20 |
30 |
|
40 |
50 |
60 |
|
|
|
|
|
|
|
|
|
|
15 |
5 |
7 |
- |
|
- |
- |
- |
12 |
|
|
|
|
|
|
|
|
|
25 |
- |
20 |
23 |
|
- |
- |
- |
43 |
|
|
|
|
|
|
|
|
|
35 |
- |
- |
30 |
|
47 |
2 |
- |
79 |
|
|
|
|
|
|
|
|
|
45 |
- |
- |
10 |
|
11 |
20 |
6 |
47 |
|
|
|
|
|
|
|
|
|
55 |
- |
- |
- |
|
9 |
7 |
3 |
19 |
|
|
|
|
|
|
|
|
|
nx |
5 |
27 |
63 |
|
67 |
29 |
9 |
n=200 |
В выделенном прямоугольнике находятся частоты наблюдаемых пар значений признаков.
Решение. Перейдем к условным вариантам. В качестве ложного нуля C1 возьмем варианту x=40, в качестве C2 - ва-
рианту y=35 , h1 =20-10=10, h2 =25-15=10.
Составим корреляционную таблицу в условных вариантах. В первом столбце вместо ложного нуля C2 пишут 0, над нулем последовательно записывают -1; -2, …; под нулем пишут 1, 2, …. В первой строке вместо ложного нуля C1 пишут
0, слева от нуля -1,-2, …; справа от нуля пишут 1,2, …. Остальные данные первоначальные.
144
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
nv |
|
|
|||
|
|
|
|
-3 |
|
|
-2 |
|
|
-1 |
|
|
0 |
|
1 |
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
5 |
|
|
7 |
|
|
|
- |
|
|
- |
|
- |
- |
|
12 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
-1 |
- |
|
|
20 |
|
|
23 |
|
- |
|
- |
- |
|
43 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
- |
|
|
- |
|
|
|
30 |
|
47 |
|
2 |
- |
|
79 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
- |
|
|
- |
|
|
|
10 |
|
11 |
|
20 |
6 |
|
47 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
- |
|
|
- |
|
|
|
- |
|
|
9 |
|
7 |
3 |
|
19 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
nu |
5 |
|
27 |
|
63 |
|
67 |
|
29 |
9 |
|
n=200 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Составим вспомогательную расчетную таблицу. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
U= |
|
|
|
||
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= nuvu |
|
|
vU |
|
|
-3 |
|
|
-2 |
|
-1 |
|
|
0 |
|
1 |
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
-2 |
|
|
5 |
|
|
7 |
|
- |
|
|
- |
|
- |
|
- |
|
|
-29 |
|
58 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
-1 |
|
|
- |
|
|
20 |
|
23 |
|
|
- |
|
- |
|
- |
|
|
-63 |
|
63 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
- |
|
|
- |
|
30 |
|
|
47 |
|
2 |
|
- |
|
|
-28 |
|
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
- |
|
|
- |
|
10 |
|
|
11 |
|
20 |
|
6 |
|
22 |
|
22 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
- |
|
|
- |
|
- |
|
|
9 |
|
7 |
|
3 |
|
13 |
|
26 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
V= |
|
|
-10 |
|
-34 |
|
-13 |
|
|
29 |
|
34 |
|
12 |
|
|
|
vU 169 |
|||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nuvv |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
uV |
|
|
30 |
|
|
68 |
|
13 |
|
|
0 |
|
34 |
|
24 |
|
uV 169 |
|
|
Кон- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
троль |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
145 |
|
|
|
|
|
|
|
|
|

Найдем u и v :
u nuu / n 5 3 27 2 63 1 29 1 9 2 / 200
0,405 ,
v nvv / n 12 2 43 1 47 1 19 2 / 200 0,09 .
Вычислим вспомогательные величины: |
||||||||||||||
|
|
2 |
n |
u 2 / n 5 9 27 4 63 1 29 1 9 4 / 200 1,405 ; |
||||||||||
u |
||||||||||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|||
|
u |
u |
1,405 0,425 |
1,106 . |
||||||||||
u |
|
|
|
|
||||||||||
Аналогично получим ~ =1,209.в
Тогда искомый выборочный коэффициент корреляции:
rв nuvuv nuv =
~ ~
n u v
= 169 200 0,425 0,09 / 200 1,106 1,209 0,603 .
Найдем x uh1 c1 0,425 10 40 35,75;
yvh2 c2 0,09 10 35 35,9 ;
~~
x h1 u 1,106 10 11,06;
~~
y h2 v 1,209 10 12,09 .
Подставив найденные величины в формулу
~
yx y rв ~y x x ,x
получим искомое уравнение
146

yx 35,9 0,60312,0911,06 x 35,75 ,
Или окончательно
yx 0,659x 12,34 .
Сравним условные средние, вычисленные: 1) по полученному уравнению; 2) по данным корреляционной таблицы. Например, при x 30 :
1)y30 0,659 30 12,34 32,11;
2)y30 23 25 30 35 10 45 / 63 32,94 .
Как видим, согласование расчетного и наблюдаемого условных средних – удовлетворительное.
Вопросы для самопроверки
1.Каковы основные задачи математической статистики?
2.Что называется выборкой? Повторные и бесповторные выборки. Какие способы отбора существуют?
3.Что называется статистическим распределением?
4.Что такое гистограмма частот?
5.Каковы числовые характеристики статистического распределения?
6.Что такое доверительный интервал? Как определить
доверительный интервал для оценки математического ожидания нормального распределения?
7.В чем состоит метод произведений для вычисления выборочной средней и дисперсии?
8.Какая гипотеза называется статистической? В чем состоят ошибки первого и второго рода?
147
9.Что называется статистическим критерием?
10.Основной принцип проверки статистических гипотез?
11.Где на практике применимо сравнение двух дисперсий нормальной генеральной совокупности? В чем оно состоит?
12.Как проверить гипотезу о равенстве неизвестной генеральной дисперсии нормальной совокупности гипотетическому значению?
13.В чем состоит задача выравнивания статистических рядов? В каких случаях применяется метод наименьших квадратов, в чем его суть?
14.Что такое критерий согласия?
15.Как вычислить теоретическую частоту нормального распределения?
16.Что такое закон распределения дискретной двумерной случайной величины?
17.Что такое условное математическое ожидание?
18.Для чего служит корреляционный момент? Что такое коэффициент корреляции? В каком случае две случайные величины называют коррелированными?
Задачи для самостоятельного решения
1. Найти доверительный интервал для оценки математического ожидания m нормального распределения
а) с надежностью 0,95, зная статистическую среднюю m =10,43, объем совокупности п =100 и среднее квадратическое отклонение =5.
б) с надежностью 0,99, зная статистическую среднюю
148

m =10,2, объем совокупности п = 16 и среднее квадратическое отклонение =4.
Ответ. а) 9,45 < m < 11,41; б) 7,63 < m < 12,77.
2. По выборке объема п =50 найдена смещенная оценка теоретической дисперсии 9,8. Найти несмещенную оценку дисперсии генеральной совокупности.
Ответ. 10.
3. В итоге четырех измерений некоторой величины одним прибором (без систематических ошибок) получены следующие результаты: 8; 9; 11; 12. Найти: а) выборочное среднее результатов измерений; б) смещенную и исправленную выборочные дисперсии ошибок прибора.
Ответ. а) 10; б) 2,5; 3,33.
4. Из нормальной генеральной совокупности извлечена выборка, состоящая из 10 наблюдений. Вычисление выборочного среднего и выборочной дисперсии дало следующие ре-
зультаты: xв 3,2 ; ~ =49. Можно ли при уровне значимости
D
0,05 отвергнуть гипотезу о том, что среднее значение исследуемой генеральной совокупности равно 3?
5.Станок–автомат штампует валики. По выборке объема
п=100 вычислено выборочное среднее диаметров изготовленных валиков. Найти с надежностью 0,95 точность, с которой выборочное среднее оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение 2 мм. Предполагается, что диаметры валиков распределены нормально.
6.По выборке из 25 упаковок товара средний вес составил101 г. с исправленным средним квадратическим отклонением 3 г. Построить доверительные интервалы для среднего и дисперсии с вероятностью 90%.
149
Приложение 1
|
|
Таблица значений функции x |
1 |
|
|
e x |
2 |
/ 2 |
|||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
|
|
8 |
|
9 |
||
0,0 |
0,3989 |
|
3989 |
3989 |
3988 |
3986 |
3984 |
3982 |
|
3980 |
|
3977 |
|
3973 |
|||
0,1 |
3970 |
|
3965 |
3961 |
3956 |
3951 |
3945 |
3939 |
|
3932 |
|
3925 |
|
3918 |
|||
0,2 |
3910 |
|
3902 |
3894 |
3885 |
3876 |
3867 |
3857 |
|
3847 |
|
3836 |
|
3825 |
|||
0,3 |
3814 |
|
3802 |
3790 |
3778 |
3765 |
3752 |
3739 |
|
3726 |
|
3712 |
|
3697 |
|||
0,4 |
3683 |
|
3668 |
3652 |
3637 |
3621 |
3605 |
3589 |
|
3572 |
|
3555 |
|
3538 |
|||
0,5 |
3521 |
|
3503 |
3485 |
3467 |
3448 |
3429 |
3410 |
|
3391 |
|
3372 |
|
3352 |
|||
0,6 |
3332 |
|
3312 |
3292 |
3271 |
3251 |
3230 |
3209 |
|
3187 |
|
3166 |
|
3144 |
|||
0,7 |
3123 |
|
3101 |
3079 |
3056 |
3034 |
3011 |
2989 |
|
2966 |
|
2943 |
|
2920 |
|||
0,8 |
2897 |
|
2874 |
2850 |
2827 |
2803 |
2780 |
2756 |
|
2732 |
|
2709 |
|
2685 |
|||
0,9 |
2661 |
|
2637 |
2613 |
2589 |
2565 |
2541 |
2516 |
|
2492 |
|
2468 |
|
2444 |
|||
1,0 |
0,2420 |
|
2396 |
2371 |
2347 |
2323 |
2299 |
227 |
|
2251 |
|
2227 |
|
2203 |
|||
1,1 |
2179 |
|
2155 |
2131 |
2107 |
2083 |
2059 |
2036 |
|
2012 |
|
1989 |
|
1965 |
|||
1,2 |
1942 |
|
1919 |
1895 |
1872 |
1849 |
1826 |
1804 |
|
1781 |
|
1758 |
|
1736 |
|||
1,3 |
1714 |
|
1691 |
1669 |
1647 |
1626 |
1604 |
1582 |
|
1561 |
|
1539 |
|
1518 |
|||
1,4 |
1491 |
|
1476 |
1456 |
1435 |
1415 |
1394 |
1374 |
|
1354 |
|
1334 |
|
1315 |
|||
1,5 |
1295 |
|
1276 |
1257 |
1238 |
1219 |
1200 |
1182 |
|
1163 |
|
1145 |
|
1127 |
|||
1,6 |
1109 |
|
1092 |
1074 |
1057 |
1040 |
1023 |
1006 |
|
0989 |
|
0973 |
|
0957 |
|||
1,7 |
0940 |
|
0925 |
0909 |
0893 |
0878 |
0863 |
0848 |
|
0833 |
|
0818 |
|
0804 |
|||
1,8 |
0790 |
|
0775 |
0761 |
0748 |
0734 |
0721 |
0707 |
|
0694 |
|
0681 |
|
0669 |
|||
1,9 |
0656 |
|
0644 |
0632 |
0620 |
0608 |
0596 |
0584 |
|
0573 |
|
0562 |
|
0551 |
|||
2,0 |
0,0540 |
|
0529 |
0519 |
0508 |
0498 |
0488 |
0478 |
|
0468 |
|
0459 |
|
0449 |
|||
2,1 |
0440 |
|
0431 |
0422 |
0413 |
0404 |
0396 |
0387 |
|
0379 |
|
0371 |
|
0363 |
|||
2,2 |
0355 |
|
0347 |
0339 |
0332 |
0325 |
0317 |
0310 |
|
0303 |
|
0297 |
|
0290 |
|||
2,3 |
0283 |
|
0277 |
0270 |
0264 |
0258 |
0252 |
0246 |
|
0241 |
|
0235 |
|
0229 |
|||
2,4 |
0224 |
|
0219 |
0213 |
0208 |
0203 |
0198 |
0194 |
|
0189 |
|
0184 |
|
0180 |
|||
2,5 |
0175 |
|
0171 |
0167 |
0163 |
0158 |
0154 |
0151 |
|
0147 |
|
0143 |
|
0139 |
|||
2,6 |
0136 |
|
0132 |
0129 |
0126 |
0122 |
0119 |
0116 |
|
0113 |
|
0110 |
|
0107 |
|||
2,7 |
0104 |
|
0101 |
0099 |
0096 |
0093 |
0091 |
0088 |
|
0086 |
|
0084 |
|
0081 |
|||
2,8 |
0079 |
|
0077 |
0075 |
0073 |
0071 |
0069 |
0067 |
|
0065 |
|
0063 |
|
0061 |
|||
2,9 |
0060 |
|
0058 |
0056 |
0055 |
0053 |
0051 |
0050 |
|
0048 |
|
0047 |
|
0046 |
|||
3,0 |
0.0044 |
|
0043 |
0042 |
0040 |
0039 |
0038 |
0037 |
|
0036 |
|
0035 |
|
0034 |
|||
3,1 |
0033 |
|
0032 |
0031 |
0030 |
0029 |
0028 |
0027 |
|
0026 |
|
0025 |
|
0025 |
|||
3,2 |
0024 |
|
0023 |
0022 |
0022 |
0021 |
0020 |
0020 |
|
0019 |
|
0018 |
|
0018 |
|||
3,3 |
0017 |
|
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
|
0014 |
|
0013 |
|
0013 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150
Продолжение прил. 1
|
0 |
1 |
2 |
3 |
4 |
5 |
б |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
3,4 |
0012 |
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
0009 |
0009 |
3,5 |
0009 |
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
0007 |
0006 |
3,6 |
0006 |
0006 |
0006 |
0005 |
0005 |
0005 |
000 |
0005 |
0005 |
0004 |
3 ,7 |
0004 |
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
0003 |
0003 |
3 ,8 |
0003 |
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
0002 |
0002 |
3,9 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0001 |
0001 |
|
|
|
|
|
|
|
|
|
|
|
151

Приложение 2
|
|
|
|
|
Ф x |
|
1 |
|
|
x |
2 |
|
|
|
Таблица значений функции |
|
|
|
e z |
|
/ 2 dz |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
Ф(х) |
x |
Ф(x) |
x |
|
Ф (x) |
|
|
x |
|
Ф (x) |
||
|
|
|
|
|
|
|
|
|
|
|
|||
0,00 |
0,0000 |
0,24 |
0,0948 |
0,48 |
|
0,1844 |
|
0,72 |
|
0,2642 |
|||
0,01 |
0,0040 |
0,25 |
0,0987 |
0,49 |
|
0,1879 |
|
0,73 |
|
0,2673 |
|||
0,02 |
0,0080 |
0,26 |
0,1026 |
0,50 |
|
0,1915 |
|
0,74 |
|
0,2703 |
|||
0,03 |
0,0120 |
0,27 |
0,1064 |
0,51 |
|
0,1950 |
|
0,75 |
|
0,2734 |
|||
0,04 |
0,0160 |
0,28 |
0,1103 |
0,5 |
|
0,1985 |
|
0,76 |
|
0,2764 |
|||
0,05 |
0,0199 |
0,29 |
0,1141 |
0,53 |
|
0,2019 |
|
0,77 |
|
0,2794 |
|||
0,06 |
0,0239 |
0,30 |
0,1179 |
0,54 |
|
0,2054 |
|
0,78 |
|
0,2823 |
|||
0,07 |
0,0279 |
0,31 |
0,1217 |
0,55 |
|
0,2088 |
|
0,79 |
|
0,2852 |
|||
0,08 |
0,0319 |
0,32 |
0,1255 |
0,56 |
|
0,2123 |
|
0,80 |
|
0,2881 |
|||
0,09 |
0,0359 |
0,33 |
0,1293 |
0,57 |
|
0,2157 |
|
0,81 |
|
0,2910 |
|||
0,10 |
0,0398 |
0,34 |
0,1331 |
0,58 |
|
0,2190 |
|
0,82 |
|
0,2939 |
|||
0,11 |
0,0438 |
0,35 |
0,1368 |
0,59 |
|
0,2224 |
|
0,83 |
|
0,2967 |
|||
0,12 |
0,0478 |
0,36 |
0,1406 |
0,60 |
|
0,2257 |
|
0,84 |
|
0,2995 |
|||
0,13 |
0,0517 |
0,37 |
0,1443 |
0,61 |
|
0,2291 |
|
0,85 |
|
0, 3023 |
|||
0,14 |
0,0557 |
0,38 |
0,1480 |
0,62 |
|
0,2324 |
|
0,86 |
|
0,3051 |
|||
0,15 |
0,0596 |
0,39 |
0,1517 |
0,63 |
|
0,2357 |
|
0,87 |
|
0,3078 |
|||
0,16 |
0,0636 |
0,40 |
0,1554 |
0,64 |
|
0,2389 |
|
0,88 |
|
0,3106 |
|||
0,17 |
0,0675 |
0,41 |
0,1591 |
0,65 |
|
0,2422 |
|
0,89 |
|
0,3133 |
|||
0,18 |
0,0714 |
0,42 |
0,1628 |
0,66 |
|
0,2454 |
|
0,90 |
|
0,3159 |
|||
0,19 |
0,0753 |
0,43 |
0,1664 |
0,67 |
|
0,2486 |
|
0,91 |
|
0,3186 |
|||
0,20 |
0,0793 |
0,44 |
0,1700 |
0,68 |
|
0,2517 |
|
0,92 |
|
0,3212 |
|||
0,21 |
0,0832 |
0,45 |
0,1736 |
0,69 |
|
0,2549 |
|
0,93 |
|
0,3238 |
|||
0,22 |
0,0871 |
0,46 |
0,1772 |
0,70 |
|
0,2580 |
|
0,94 |
|
0,3264 |
|||
0,23 |
0,0910 |
0,47 |
0,1808 |
0,71 |
|
0,2611 |
|
0,95 |
|
0,3289 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
152
Продолжение прил. 2
x |
Ф (x) |
x |
Ф(x) |
|
x |
Ф(x) |
x |
Ф(x) |
|
|
|
|
|
|
|
|
|
0,96 |
0,3315 |
1,37 |
0,4147 |
|
1,78 |
0,4025 |
2,30 |
0,4909 |
0,97 |
0,3340 |
1 ,38 |
0,4162 |
|
1,79 |
0,4633 |
2.38 |
0,4913 |
0,98 |
0,3365 |
1,39 |
0,4177 |
|
1,80 |
0,4641 |
2,40 |
0,4918 |
0,99 |
0,3389 |
1,40 |
0,4192 |
|
1,81 |
0,4649 |
2,42 |
0,4922 |
1,00 |
0,3413 |
1,41 |
0,4207 |
|
1,82 |
0,4056 |
2,44 |
0,4927 |
1,01 |
0,3438 |
1,42 |
0,4222 |
|
1,83 |
0,4664 |
2,46 |
0,4931 |
1,02 |
0,3401 |
1,43 |
0,4230 |
|
1,84 |
0,4671 |
2,48 |
0,4934 |
1,03 |
0,3485 |
1,44 |
0,4251 |
|
1,85 |
0,4678 |
2,50 |
0,4938 |
1,04 |
0,3508 |
1,45 |
0,4265 |
|
1,86 |
0,4686 |
2,52 |
0,4941 |
1,05 |
0.3531 |
1,46 |
0,4279 |
|
1,87 |
0.4693 |
2,54 |
0,4945 |
1,06 |
0,3554 |
1,47 |
0,4292 |
|
1,88 |
0,4699 |
2,50 |
0,4948 |
1,07 |
0,3577 |
1,48 |
0,4305 |
|
1,89 |
0,4706 |
2,58 |
0,4951 |
1,08 |
0,3599 |
1,49 |
0,4319 |
|
1,90 |
0,4713 |
2,60 |
0,4953 |
1,09 |
0,3621 |
1,50 |
0,4332 |
|
1,91 |
0,4719 |
2,62 |
0,4956 |
1,10 |
0,3643 |
1,51 |
0.4345 |
|
1,92 |
0,4726 |
2,64 |
0,4959 |
1,11 |
0,3665 |
1,52 |
0,4357 |
|
1,93 |
0,4732 |
2,66 |
0,4961 |
1,12 |
0.3686 |
1,53 |
0,4370 |
|
1,94 |
0,4738 |
2,68 |
0,4963 |
1,13 |
0,3708 |
1,54 |
0,4382 |
|
1,95 |
0,4744 |
2,70 |
0,4965 |
1,14 |
0,3729 |
1,55 |
0,4394 |
|
1,96 |
0,4750 |
2,72 |
0,4967 |
1,15 |
0,3749 |
1,50 |
0,4406 |
|
1,97 |
0,4750 |
2,74 |
0,4969 |
1,16 |
0,3770 |
1,57 |
0,4418 |
|
1,98 |
0,4761 |
2,76 |
0,4971 |
1,17 |
0,3790 |
1,58 |
0,4429 |
|
1,99 |
0,4767 |
2,78 |
0,4973 |
1,18 |
0,3810 |
1,59 |
0,4441 |
|
2,00 |
0,4772 |
2,80 |
0,4974 |
1,19 |
0,3830 |
1,60 |
0,4452 |
|
2,02 |
0,4783 |
2,82 |
0,4976 |
1,20 |
0,3849 |
1,61 |
0,4463 |
|
2,04 |
0,4793 |
2,84 |
0,4977 |
1,21 |
0,3869 |
1,62 |
0,4474 |
|
2,00 |
0,4803 |
2,86 |
0,4979 |
1,22 |
0.3883 |
1,03 |
0,4484 |
|
2,08 |
0,4812 |
2,88 |
0,4980 |
1,23 |
0,3907 |
1,64 |
0,4495 |
|
2,10 |
0,4821 |
2,90 |
0,4981 |
1,24 |
0,3925 |
1,65 |
0,4505 |
|
2,12 |
0,4830 |
2,92 |
0,4982 |
1,25 |
0,3944 |
1,66 |
0,4515 |
|
2,14 |
0,4838 |
2,94 |
0,4984 |
1,26 |
0,3962 |
1,67 |
0,4525 |
|
2,16 |
0,4846 |
2,96 |
0,4985 |
1,27 |
0,3980 |
1,68 |
0,4535 |
|
2,1 |
0,4854 |
2,98 |
0,4986 |
|
|
|
153 |
|
|
|
|
|
Окончание прил. 2
x |
Ф (x) |
x |
Ф(x) |
x |
|
Ф(x) |
|
x |
|
Ф(x) |
1,28 |
0,3997 |
1,69 |
0,4545 |
2,20 |
0,4801 |
3,00 |
0,49865 |
|||
1,29 |
0,4015 |
1,70 |
0,4554 |
2,22 |
0,4868 |
3,20 |
0,49931 |
|||
1,30 |
0,4032 |
1,71 |
0,4504 |
2,24 |
0,4875 |
3,40 |
0,49966 |
|||
1,31 |
0,4049 |
1,72 |
0,4573 |
2,26 |
0,4881 |
3.60 |
0,499841 |
|||
1,32 |
0,4066 |
1,73 |
0,4582 |
2,28 |
0,4887 |
3,80 |
0,499928 |
|||
1,33 |
0,4082 |
1,74 |
0,4591 |
2,30 |
0,4893 |
4.00 |
0,499968 |
|||
1,34 |
0,4099 |
1,75 |
0,4599 |
2,32 |
0,4898 |
4,50 |
0,499997 |
|||
1,35 |
0,4115 |
1,76 |
0,4608 |
2,34 |
0,4904 |
5,00 |
0,499997 |
|||
1,36 |
0,4131 |
1,77 |
0,4016 |
|
|
|
|
|
|
|
154
|
|
|
|
|
|
|
|
Приложение 3 |
||
|
|
|
Таблица значений t t , n |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
0.95 |
|
0,99 |
0.999 |
n |
0,95 |
0.99 |
0.999 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
2,78 |
|
4,60 |
8,61 |
20 |
2,093 |
2.861 |
|
3,883 |
|
6 |
2,57 |
|
4,03 |
6,86 |
25 |
2,064 |
2,797 |
|
3.745 |
|
7 |
2,45 |
|
3,71 |
5,96 |
30 |
2,045 |
2,756 |
|
3,659 |
|
8 |
2,37 |
|
3,50 |
5,41 |
35 |
2.032 |
2,720 |
|
3,600 |
|
9 |
2,31 |
|
3,36 |
5,04 |
40 |
2,023 |
2.708 |
|
3,558 |
|
10 |
2,26 |
|
3,25 |
4,78 |
45 |
2,016 |
2,692 |
|
3,527 |
|
11 |
2,23 |
|
3,17 |
4,59 |
50 |
2,009 |
2,679 |
|
3,502 |
|
12 |
2.20 |
|
3,11 |
4.44 |
60 |
2,001 |
2,662 |
|
3,464 |
|
13 |
2,18 |
|
3,06 |
4,32 |
70 |
1,996 |
2,649 |
|
3,439 |
|
14 |
2,16 |
|
3,01 |
4,22 |
80 |
1,001 |
2,640 |
|
3,418 |
|
15 |
2,15 |
|
2,98 |
4,14 |
90 |
1,987 |
2,633 |
|
3,403 |
|
16 |
2.13 |
|
2,95 |
4,07 |
100 |
1,984 |
2,627 |
|
3,392 |
|
17 |
2.12 |
|
2,92 |
4,02 |
120 |
1,980 |
2.617 |
|
3,374 |
|
18 |
2.11 |
|
2,90 |
3,97 |
|
1,960 |
2.576 |
|
3,291 |
|
19 |
2,10 |
|
2,88 |
3,92 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155 |
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 4 |
||
|
|
Таблица значений |
q q , n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
0.95 |
0.99 |
0.999 |
n |
|
0.95 |
0.99 |
0,999 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1,37 |
2,67 |
5,64 |
20 |
|
0,37 |
0,58 |
0,88 |
|
6 |
1,09 |
2,01 |
3,88 |
25 |
|
0,32 |
0,49 |
0,73 |
|
7 |
0,92 |
1,62 |
2,98 |
30 |
|
0,28 |
0,43 |
0,63 |
|
8 |
0,80 |
1,38 |
2,42 |
35 |
|
0,26 |
0,38 |
0,56 |
|
9 |
0,71 |
1,20 |
2,06 |
40 |
|
0.24 |
0,35 |
0,50 |
|
10 |
0,65 |
1,08 |
1,80 |
45 |
|
0,22 |
0,32 |
0,46 |
|
11 |
0,59 |
0,98 |
1,60 |
50 |
|
0,21 |
0,30 |
0,43 |
|
12 |
0,55 |
0,90 |
1,45 |
60 |
|
0,188 |
0,269 |
0,38 |
|
13 |
0.52 |
0,83 |
1,33 |
70 |
|
0,174 |
0,245 |
0,34 |
|
14 |
0.48 |
0,78 |
1,23 |
80 |
|
0.161 |
0,226 |
0,31 |
|
15 |
0,46 |
0,73 |
1,15 |
90 |
|
0.151 |
0,211 |
0,29 |
|
16 |
0,44 |
0,70 |
1,07 |
100 |
|
0.143 |
0.198 |
0,27 |
|
17 |
0,42 |
0,66 |
1,01 |
150 |
|
0.115 |
0,160 |
0,211 |
|
18 |
0,40 |
0,63 |
0,96 |
200 |
|
0,099 |
0.136 |
0,185 |
|
19 |
0,39 |
0,60 |
0,92 |
250 |
|
0,089 |
0,120 |
0,162 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
156 |
|
|
|
|
|
Приложение 5
Критические точки распределения 2
Число степеней свободы |
|
Уровень значимости |
|
|||
k |
|
|
|
|
|
|
|
0,01 |
0,025 |
0,05 |
0,95 |
0,975 |
0,89 |
|
|
|
|
|
|
|
1 |
6,6 |
5,0 |
3,8 |
0,0039 |
0,00098 |
0,00016 |
2 |
9,2 |
7,4 |
6,0 |
0,103 |
0,051 |
0,020 |
3 |
11,3 |
9,4 |
7,8 |
0,352 |
0,216 |
0,115 |
4 |
13,3 |
11,1 |
9,5 |
0,711 |
0,484 |
0,297 |
5 |
15,1 |
12,8 |
11,1 |
1,15 |
0,831 |
0,554 |
6 |
16,8 |
14,4 |
12,6 |
1,64 |
1,24 |
0,872 |
7 |
18,5 |
16,0 |
14,1 |
2,17 |
1,69 |
1,24 |
8 |
20,1 |
17,5 |
15,5 |
2,73 |
2,18 |
1,65 |
9 |
21,7 |
19,0 |
16,9 |
3,33 |
2,70 |
2,09 |
10 |
23,2 |
20,5 |
18,3 |
3,94 |
3,25 |
2,56 |
11 |
24,7 |
21,9 |
19,7 |
4,57 |
3,82 |
3,05 |
12 |
26,2 |
23,3 |
21,0 |
5,23 |
4,40 |
3,57 |
13 |
27,7 |
24,7 |
22,4 |
5,89 |
5,01 |
4,11 |
14 |
29,1 |
26,1 |
23,7 |
6,57 |
5,63 |
4,66 |
15 |
30,6 |
27,5 |
25,0 |
7,26 |
6,26 |
5,23 |
16 |
32,0 |
28,8 |
26,3 |
7,96 |
6,91 |
5,81 |
17 |
33,4 |
30,2 |
27,6 |
8,67 |
7,56 |
6,41 |
18 |
34,8 |
31,5 |
28,9 |
9,39 |
8,23 |
7,01 |
19 |
36,2 |
32,5 |
30,1 |
10,1 |
8,91 |
7,63 |
20 |
37,6 |
34,2 |
31,4 |
10,9 |
9,59 |
8,26 |
21 |
38,9 |
35,5 |
32,7 |
11,6 |
10,3 |
8,90 |
22 |
40,3 |
36,8 |
33,9 |
12,3 |
11,0 |
9,54 |
23 |
41,6 |
38,1 |
35,2 |
13,1 |
11,7 |
10,2 |
24 |
43,0 |
39,4 |
36,4 |
13,8 |
12,4 |
10,9 |
25 |
44,3 |
40,6 |
37,7 |
14,6 |
13,1 |
11,5 |
26 |
45,6 |
41,9 |
38,9 |
15,4 |
13,8 |
12,2 |
27 |
47,0 |
43,2 |
40,1 |
16,2 |
14,6 |
12,9 |
28 |
48,3 |
44,5 |
41,3 |
16,9 |
15,3 |
13,6 |
29 |
49,6 |
45,7 |
42,6 |
17,7 |
16,0 |
14,3 |
30 |
50,9 |
47,0 |
43,8 |
18,5 |
16,8 |
15,0 |
|
|
|
|
|
|
|
157
Приложение 6
Критические точки распределения Стьюдента
|
Уровень значимости (двусторонняя критическая |
|||||
Число степеней |
|
|
область) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
свободы k |
0,10 |
0,05 |
0,02 |
0,01 |
0,002 |
0,001 |
|
||||||
|
|
|
|
|
|
|
1 |
6,31 |
12,7 |
31,82 |
63,7 |
318,3 |
637,0 |
2 |
2,92 |
4,30 |
6,97 |
9,92 |
22,33 |
31,6 |
3 |
2,35 |
3,18 |
4,54 |
5,84 |
10,22 |
12,9 |
4 |
2,13 |
2,78 |
3,75 |
4,60 |
7,17 |
8,61 |
5 |
2,01 |
2,57 |
3,37 |
4,03 |
5,89 |
6,86 |
6 |
1,94 |
2,45 |
3,14 |
3,71 |
5,21 |
5,96 |
7 |
1,89 |
2,36 |
3,00 |
3,50 |
4,79 |
5,40 |
8 |
1,86 |
2,31 |
2,90 |
3,36 |
4,50 |
5,04 |
9 |
1,83 |
2,26 |
2,82 |
3,25 |
4,30 |
4,78 |
10 |
1,81 |
2,23 |
2,76 |
3,17 |
4,14 |
4,59 |
11 |
1,80 |
2,20 |
2,72 |
3,11 |
4,03 |
4,44 |
12 |
1,78 |
2,18 |
2,68 |
3,05 |
3,93 |
4,32 |
13 |
1,77 |
2,16 |
2,65 |
3,01 |
3,85 |
4,22 |
14 |
1,76 |
2,14 |
2,62 |
2,98 |
3,79 |
4,14 |
15 |
1,75 |
2,13 |
2,60 |
2,95 |
3,73 |
4,07 |
16 |
1,75 |
2,12 |
2,58 |
2,92 |
3,69 |
4,01 |
17 |
1,74 |
2,11 |
2,57 |
2,90 |
3,65 |
3,96 |
18 |
1,73 |
2,10 |
2,55 |
2,88 |
3,61 |
3,92 |
19 |
1,73 |
2,09 |
2,54 |
2,86 |
3,58 |
3,88 |
20 |
1,73 |
2,09 |
2,53 |
2,85 |
3,55 |
3,85 |
21 |
1,72 |
2,08 |
2,52 |
2,83 |
3,53 |
3,82 |
22 |
1,72 |
2,07 |
2,51 |
2,82 |
3,51 |
3,79 |
23 |
1,71 |
2,07 |
2,50 |
2,81 |
3,49 |
3,77 |
24 |
1,71 |
2,06 |
2,49 |
2,80 |
3,47 |
3,74 |
25 |
1,71 |
2,06 |
2,49 |
2,79 |
3,45 |
3,72 |
26 |
1,71 |
2,06 |
2,48 |
2,78 |
3,44 |
3,71 |
27 |
1,71 |
2,05 |
2,47 |
2,77 |
3,42 |
3,69 |
28 |
1,70 |
2,05 |
2,46 |
2,76 |
3,40 |
3,66 |
29 |
1,70 |
2,05 |
2,46 |
2,76 |
3,40 |
3,66 |
30 |
1,70 |
2,04 |
2,46 |
2,75 |
3,39 |
3,65 |
40 |
1,68 |
2,02 |
2,42 |
2,70 |
3,31 |
3,55 |
60 |
1,97 |
2,00 |
2,39 |
2,66 |
3,23 |
3,46 |
120 |
1,66 |
1,98 |
2,36 |
2,62 |
3,17 |
3,37 |
∞ |
1,64 |
1,96 |
2,33 |
2,58 |
3,09 |
3,29 |
|
|
|
|
|
|
|
|
0.05 |
0.025 |
0.01 |
0.005 |
0.001 |
0.0005 |
|
|
|
|
|
|
|
|
|
|
Уровень значимости α |
|
||
|
|
(односторонняя критическая область) |
||||
|
|
|
|
|
|
|
158
Приложение 7
Критические точки распределения F Фишера–Снедекора
( k1 – число степеней свободы большей дисперсии, k2 – число степеней свободы меньшей дисперсии)
|
|
|
|
|
Уровень значимости |
= 0,01 |
|
|
|
||||
k2 |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 9 |
10 |
1 1 |
12 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4052 |
4999 |
|
5403 |
5625 |
5764 |
5889 |
5928 |
5981 |
6022 |
6056 |
6082 |
6106 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
98.49 |
99,01 |
|
99,17 |
99,25 |
99,30 |
99,33 |
99,34 |
99,36 |
99,38 |
99,40 |
99,41 |
99,42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
34,12 |
30,81 |
|
29,46 |
28,71 |
28,24 |
27,91 |
27,67 |
27,49 |
27,34 |
27,23 |
27,13 |
27,05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
21.20 |
18,00 |
|
16,69 |
15.98 |
15,52 |
15,21 |
14,98 |
14,80 |
14,66 |
14,54 |
14,45 |
14,37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
16,26 |
13,27 |
|
12,06 |
11,39 |
10,97 |
1 0 67 |
10,45 |
10,27 |
10,15 |
10,05 |
9,С6 |
9,89 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
13,74 |
10,92 |
|
9,78 |
9,15 |
8,75 |
8,47 |
8,26 |
8,10 |
7,98 |
7,87 |
7,79 |
7,72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
12,25 |
9,55 |
|
8,45 |
7,85 |
7,46 |
7,19 |
7,00 |
6,84 |
6,71 |
6,62 |
6,54 |
6,47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
11,26 |
8,65 |
|
7,59 |
7,01 |
6,63 |
6,37 |
6,19 |
6,03 |
5,91 |
5,82 |
5,74 |
5,67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
10,56 |
8,02 |
|
6,99 |
6,42 |
6,06 |
5,80 |
5,62 |
5.47 |
5,35 |
5,26 |
5,18 |
5,11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
10,04 |
7,56 |
|
6,55 |
5,99 |
5,64 |
5,39 |
5,2! |
5.06 |
4,95 |
4,85 |
4,78 |
4,71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
9,86 |
7,20 |
|
6.22 |
5,67 |
5,32 |
5,07 |
4,88 |
4,74 |
4,63 |
4,54 |
4,46 |
4,40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
9,33 |
6,93 |
|
5,95 |
5,41 |
5,06 |
4,82 |
4,65 |
4,50 |
4,39 |
4,30 |
4,22 |
4,16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
9.07 |
6,70 |
|
5,74 |
5,20 |
4,86 |
4,62 |
4,44 |
4,30 |
4,19 |
4,10 |
4,02 |
3,96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
8,86 |
6,51 |
|
5,56 |
5,03 |
4,69 |
4,46 |
4,28 |
4,14 |
4,03 |
3,94 |
3,86 |
3,80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
8,68 |
6,36 |
|
5,42 |
4,89 |
4,56 |
4.32 |
4,14 |
4,00 |
3,89 |
3,80 |
3,73 |
3,67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
8,53 |
6,23 |
|
5,29 |
4,77 |
4,44 |
4,20 |
4,03 |
3,89 |
3,78 |
3,69 |
3,61 |
3,55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
8,40 |
6,11 |
|
5,18 |
4,67 |
4,34 |
4,10 |
3,93 |
3,79 |
3,68 |
3,59 |
3,52 |
3,45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
159

Продолжение прил. 7
|
|
|
|
|
|
|
|
Уровень значимости |
=0,05 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
k2 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
k1 |
8 |
|
9 |
|
10 |
|
11 |
|
12 |
||||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
161 |
|
200 |
|
216 |
|
225 |
|
230 |
234 |
|
|
237 |
239 |
|
241 |
|
242 |
|
243 |
|
244 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
18,51 |
|
19,00 |
19,16 |
|
19,25 |
|
19,30 |
19,33 |
|
|
19,36 |
19,37 |
|
19,38 |
|
19,39 |
19,40 |
|
19,41 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
10.13 |
|
9.55 |
|
9,28 |
|
9,12 |
|
9,01 |
8,94 |
|
|
8,88 |
8,84 |
|
8,81 |
|
8,78 |
|
8,76 |
|
8,74 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
7,71 |
|
6,94 |
|
6,59 |
|
6,39 |
|
6,26 |
6,16 |
|
|
6,09 |
6,04 |
|
6,00 |
|
5,96 |
|
5,93 |
|
5,91 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5 |
6,61 |
|
|
5,79 |
|
5,41 |
|
5,19 |
|
|
5,05 |
4,95 |
|
|
4,88 |
4,82 |
|
|
4,78 |
|
|
4,74 |
|
4,70 |
|
|
4,68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6 |
5,99 |
|
|
5,14 |
|
4,76 |
|
4,53 |
|
|
4,39 |
4,28 |
|
|
4,21 |
4,15 |
|
|
4,10 |
|
|
4,06 |
|
4,03 |
|
|
4,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7 |
5,59 |
|
|
4,74 |
|
4,35 |
|
4,12 |
|
|
3,97 |
3,87 |
|
|
3,79 |
3,73 |
|
|
3,68 |
|
|
3,63 |
|
3,60 |
|
|
3,57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8 |
5,32 |
|
|
4,46 |
|
4,07 |
|
3,84 |
|
|
3,69 |
3,58 |
|
|
3,50 |
3,44 |
|
|
3,39 |
|
|
3,34 |
|
3,31 |
|
|
3,28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9 |
5,12 |
|
|
4,26 |
|
3,86 |
|
3,63 |
|
|
3,48 |
3,37 |
|
|
3,29 |
3,23 |
|
|
3,18 |
|
|
3,13 |
|
3,10 |
|
|
3,07 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
10 |
4,96 |
|
|
4,10 |
|
3,71 |
|
3,48 |
|
|
3,33 |
3,22 |
|
|
3,14 |
3,07 |
|
|
3,02 |
|
|
2,97 |
|
2,94 |
|
|
2,91 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11 |
4.84 |
|
|
3,98 |
|
3,59 |
|
3,36 |
|
|
3,20 |
3,09 |
|
|
3,01 |
2,95 |
|
|
2,90 |
|
|
2,86 |
|
2,82 |
|
|
2,79 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
12 |
4,75 |
|
|
3,88 |
|
3,49 |
|
3,26 |
|
|
3,11 |
3,00 |
|
|
2,92 |
2,85 |
|
|
2,80 |
|
|
2,76 |
|
2,72 |
|
|
2,69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13 |
4,67 |
|
|
3,80 |
|
3,41 |
|
3,18 |
|
|
3,02 |
2,92 |
|
|
2,84 |
2,77 |
|
|
2,72 |
|
|
2,67 |
|
2,63 |
|
|
2,60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
14 |
4,60 |
|
|
3,74 |
|
3,34 |
|
3,11 |
|
|
2,96 |
2,85 |
|
|
2,77 |
2,70 |
|
|
2,65 |
|
|
2,60 |
|
2,56 |
|
|
2,53 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
15 |
4,54 |
|
|
3,68 |
|
3,29 |
|
3,06 |
|
|
2,90 |
2,79 |
|
|
270 |
2,64 |
|
|
2,59 |
|
|
2,55 |
|
2,51 |
|
|
2,48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16 |
4,49 |
|
|
3,63 |
|
3.24 |
|
3,01 |
|
|
2,85 |
2,74 |
|
|
2,66 |
2,59 |
|
|
2,54 |
|
|
2,49 |
|
2,45 |
|
|
2,42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
17 |
4.45 |
|
|
3,59 |
|
3.20 |
|
2,90 |
|
|
2,81 |
2,70 |
|
|
2,62 |
2,55 |
|
|
$,50 |
|
|
2,45 |
|
2,41 |
|
|
2,38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
160
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Вентцель Е.С. Теория вероятностей / Е.С. Вентцель.
М.: Высш. шк, 2001.
2.Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. М.: Высш. шк., 1972.
3.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман.
М.: Высш. шк., 1979.
4.Данко П.Е. Высшая математика в упражнениях и зада-
чах: учеб. пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. М.: Высш. шк., 1996. Ч.2.
161
ОГЛАВЛЕНИЕ Введение………………………………………………... 3
1.Элементы теории вероятностей…………………….. 4
1.1.Предмет теории вероятностей………………….. 4
1.2.Основные понятия теории вероятностей………. 5
1.3. Классическое определение вероятности………. |
7 |
1.4.Основные формулы комбинаторики…………… |
9 |
1.5. Относительная частота. Устойчивость относи- |
|
тельной частоты……………………………………… |
11 |
1.6.Ограниченность классического определения вероятности. Статистическая вероятность……………. 12
1.7.Теорема сложения вероятностей. Теорема сло-
жения вероятностей несовместных событий………. |
13 |
1.8.Противоположные события…………………….. 15
1.9.Принцип практической невозможности малове-
роятных событий……………………………………… |
16 |
1.10. Теорема умножения вероятностей. Произведе- |
|
ние событий…………………………………………… |
17 |
1.11.Условная вероятность…………………………... 17
1.12.Теорема умножения вероятностей…………….. 18
1.13.Независимые события. Теорема умножения для
независимых событий………………………………… |
20 |
1.14. Вероятность появления хотя бы одного собы- |
|
тия……………………………………………………… |
23 |
1.15. Следствия теорем сложения и умножения. Тео- |
|
рема сложения вероятностей совместных событий… |
24 |
1.16.Формула полной вероятности………………….. 25
1.17.Вероятность гипотез. Формулы Бейеса………... 27
1.18.Повторение испытаний. Формула Бернулли….. 29
1.19.Локальная теорема Лапласа…………………….. 32
1.20. Интегральная теорема Лапласа………………… |
33 |
1.21.Распределение Пуассона………………………… |
34 |
1.22. Случайные величины. Виды случайных вели- |
|
чин. Задание дискретной случайной величины……... |
36 |
162 |
|
1.22.1.Случайная величина………………………….. 36
1.22.2.Закон распределения вероятностей дискрет-
ной случайной величины…………………………….. 37
1.22.3.Биномиальное распределение……………….. 39
1.22.4.Числовые характеристики дискретных случайных величин. Математическое ожидание дискретной случайной величины……………………….. 40
1.22.5. Дисперсия дискретной случайной величины |
44 |
1.22.6. Среднее квадратическое отклонение……….... |
47 |
1.22.7.Функция распределения вероятностей случай- |
|
ной величины……………………………...................... |
47 |
1.22.8.Числовые характеристики непрерывных слу-
чайных величин……………………………………….. 51
1.22.9.Нормальное распределение…………………… 52
1.22.10.Вероятность попадания в заданный интервал нормальной случайной величины…………………..... 53
Вопросы для самопроверки……………………………… 55
Задачи для самостоятельного решения ………………… |
56 |
2. Элементы математической статистики……………. |
63 |
2.1. Генеральная совокупность, выборка…………… |
64 |
2.2.. Статистический ряд. Гистограмма……………. |
68 |
2.3. Числовые характеристики статистического рас- |
|
пределения. Обработка опытов…………………….. |
73 |
2.4. Доверительный интервал. Доверительная вероят- |
|
ность………………………………………………….…. 80
2.5. Методы расчета сводных характеристик выбор- |
|
ки……………………………………………………… |
89 |
2.6. Построение нормальной кривой по опытным |
|
данным………………………………………………… |
93 |
2.7. Проверка статистических гипотез……………… |
94 |
2.8. Сравнение двух дисперсий нормальных гене- |
|
163 |
|
ральных совокупностей……………………………… |
99 |
|
2.9. Сравнение исправленной выборочной дисперсии |
|
|
с гипотетической генеральной дисперсией нормаль- |
103 |
|
ной совокупности…………………………………….. |
||
|
||
2.10. Выравнивание статистических рядов………… |
106 |
|
2.11. Критерии согласия……………………………… |
112 |
|
2.12. Методика вычисления теоретических частот |
|
|
нормального распределения……………………..…… |
118 |
|
2.13. Система двух случайных величин…………… |
123 |
|
2.13.1. Понятие о системе нескольких случай- |
|
|
ных величин……………………..…………………. |
123 |
|
2.13.2. Закон распределения вероятностей дис- |
|
|
кретной двумерной случайной величины………. |
124 |
|
2.13.3. Вероятность попадания случайной точки |
|
|
в полуполосу…………………………………... |
126 |
|
2.13.4. Вероятность попадания случайной точки |
|
|
в прямоугольник……………………………….. |
127 |
|
2.13.5. Плотность совместного распределения ве- |
|
|
роятностей непрерывной двумерной случайной |
|
|
величины (двумерная плотность вероятности)…… |
128 |
|
2.13.6. Условные законы распределения состав- |
|
|
ляющих системы дискретных случайных вели- |
|
|
чин………………………………………………… |
129 |
|
2.13.7. Условное математическое ожидание…… |
130 |
|
2.13.8. Числовые характеристики системы двух |
|
|
случайных величин. Корреляционный момент. |
|
|
Коэффициент корреляции……………………… |
132 |
|
2.13.9. Линейная регрессия. Прямые линии |
|
|
среднеквадратической регрессии………………. |
135 |
|
2.14. Элементы теории корреляции………………. |
136 |
|
2.14.1. Отыскание параметров выборочного урав- |
|
|
нения прямой линии среднеквадратической рег- |
|
|
рессии по несгруппированным данным………… |
138 |
|
2.14.2. Отыскание параметров выборочного урав- |
|
|
164 |
|
нения прямой линии регрессии по сгруппированным данным. Проверка гипотезы о значимости выборочного коэффициента корреляции. Методика вычисления выборочного коэффициента корре-
ляции………………………………………………. 140
Вопросы для самопроверки……………………………… 147 Задачи для самостоятельного решения………………… 148
Приложение 1…………………………………………….. 150 Приложение 2…………………………………………….. 152 Приложение 3…………………………………………….. 155 Приложение 4……………………………………………. 156 Приложение 5……………………………………………. 157 Приложение 6……………………………………………. 158 Приложение 7……………………………………………. 159
Библиографический список…………………………… 161
165
Учебное издание
Дурова Валентина Николаевна Зайцева Марина Ивановна Соколова Ольга Анатольевна
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ИМАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Вавторской редакции Компьютерный набор О.А. Соколовой
Подписано к изданию 25.04.2012. Уч.- изд. л. 9,0.
ФГБОУ ВПО «Воронежский государственный технический университет»
394026 Воронеж, Московский просп., 14
