P6 4 C6 4 p 4 q6 4 4! 2!6! 0,75 4 0,25 2

4! 5 6 0,75 4 0,25 2 0,30. 4! 1 2

1.19. Локальная теорема Лапласа

Выше была выведена формула Бернулли, позволяющая вычислить вероятность того, что событие появится в п испытаниях ровно k раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях п достаточно трудно, так как формула требует выполнения действий над громадными числами.

Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико.

Локальная теорема Лапласа. Если вероятность р появ-

ления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рn (k) того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

при x k np / npq .

Имеются таблицы, в которых помещены значения функции x , соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются

32

теми же таблицами, так как функция x четна, т. е. x x .

Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна

Формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях п.

Пример. 1.27. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.

Р е ш е н и е . По условию, n = 400; k = 80; р = 0,2; q = 0,8.

Воспользуемся формулой Лапласа:

где x k np / npq 80 400 0,2 / 8 0.

По таблице приложения 1 находим 0 0,3989. Ис-

комая вероятность P400 80 18 0,3989 0,04986.

1.20. Интегральная теорема Лапласа

Вновь предположим, что производится п испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычислить вероятность Рп (k1, k2) того, что событие А появится в п испытаниях не менее k1 и не более k2 раз (для краткости будем говорить «от k1 до k2 раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.

33

Теорема. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рп (k1, k2) того, что событие А появится в п испытаниях от k1 до k2 раз, приближенно равна определенному интегралу

При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами. В таблице даны значения функции Лапласа

для неотрицательных значений х; для х < 0 пользуются той же таблицей, зная, что функция Ф (х) нечетна, т. е.Ф(-х)= - Ф (х). В таблице приведены значения интеграла лишь до х = 5, а для х > 5 можно принять Ф (х) = 0,5. Функцию Ф (х) часто называют

функцией Лапласа.

Итак, вероятность того, что событие А появится в п независимых испытаниях от k1 до k2 раз,

Pn k1, k2 Ф x - Ф x , где x k1 np / 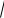npq , x k2 np / npq .

1.21. Распределение Пуассона

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях

34

используют формулу Бернулли. Если же п велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала ( p 0,1). В этих

случаях (п велико, р мало) прибегают к асимптотической формуле Пуассона

Здесь сделано важное допущение: произведение пр сохраняет постоянное значение, а именно пр = k. Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях п, остается неизменным.

Итак, вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз, вычисляется с помощью формулы Пуассона (1.6).

Пример. 1.28. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.

Р е ш е н и е . По условию, п = 5000, р = 0,0002, k = 3.

Найдем :

= пр = 5000 • 0,0002 = 1.

По формуле Пуассона искомая вероятность приближенно равна

P5000 3 k e / k!= e 1 / 3! 1/ 6e 0,06.

35

1.22. Случайные величины. Виды случайных величин. Задание дискретной случайной величины

1.22.1. Случайная величина

Рассмотрим пример, когда при бросании игральной кости могут появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, ..., 100.

Пример. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а,b).

В первом из примеров случайная величина X могла принять одно из следующих возможных значений: 0, 1, 2, ..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений X. Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. Во втором примере случайная величина могла принять любое из значений промежутка (а, в). Здесь нельзя отделить одно возможное значение от другого промежутком, не со-

36

держащим возможных значений случайной величины.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Будем далее обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения - соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x1 x2, х3.

1.22.2. Закон распределения вероятностей дискретной случайной величины

Случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их — различные. Поэтому для задания дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины

называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

37

X xl х2 . . . хп

Рр1 р2 рп

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X = , X = , . . ., X =хп образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице.

Пример 1.29. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.

Р е ш е н и е . Напишем возможные значения X: х1 = 50, x2= 1, х3 = 0. Вероятности этих возможных значений таковы:

р1 = 0,01. р2 = 0,1, p3= l-(p1 + p2) = 0.89.

Тогда искомый закон распределения

X50 1 ... 0

Р0,01 0,1 0,89

Контроль: 0,01+0,1+0,89=1.

Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, рi), а затем соединяют их отрезками прямых. Полученную фигуру называ-

ют многоугольником распределения.

38

1.22.3. Биномиальное распределение

Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность не появления q=1-р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Необходимо найти закон распределения величины X. Для этого требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, . . . , либо п раз. Таким образом, возможные значения X таковы: х1 = 0, x 2 = l , x3 = 2, . . . , хп+1 = п. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли (1.4). Она и является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли.

Напишем биномиальный закон в виде таблицы:

Пример 1.30. Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.

Р е ш е н и е . Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу кредитов можно считать за n=5 независимых событий. Вероятность невозврата k кредитов из 5 описывается биномиальным распределением и рассчитывается по формуле Бернулли (1.4), где p=0,2, q=0,8, k

39

принимает значения от нуля до 5:

Контроль: 0,00032+0,0064+0,0512+0,2048+0,4096+0,32768=1.

1.22.4.Числовые характеристики дискретных случайных величин. Математическое ожидание дискретной случайной величины

Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа назы-

вают числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.

Математическое ожидание, приближенно равно среднему значению случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у

40

первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическим ожиданием дискретной случайной вели-

чины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только значения xl, х2, . . ., хп, вероятности которых соответственно равны р1, р2, . . ., рп.. Тогда математическое ожидание М (X) случайной величины X определяется равенством

М (X) = х1 р1 + х2 р2 + . . . + хп рп.

Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Пример 1.31. Найти математическое ожидание случайной величины X, зная закон ее распределения:

р0,1 0,6 0,3.

Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

М(Х)= 3 0,1 5 0,6 2 0,3 =3,9.

Вероятностный смысл математического ожидания: мате-

матическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины, т.е. на числовой оси

41