
- •1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- •1.1. Предмет теории вероятностей
- •1.2. Основные понятия теории вероятностей
- •1.3. Классическое определение вероятности
- •1.8. Противоположные события
- •1.11. Условная вероятность
- •Замечание. Справедливо равенство
- •Искомая вероятность
- •Искомая вероятность
- •1.16. Формула полной вероятности
- •1.17. Вероятность гипотез. Формулы Байеса
- •Отсюда
- •1.19. Локальная теорема Лапласа
- •1.20. Интегральная теорема Лапласа
- •1.21. Распределение Пуассона
- •Пример 1.32. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 120 тыс. ден. ед., а число продаж X автомашин в течение дня подчиняется закону распределения
- •Искомая характеристика М(П) находится с использованием указанных ранее свойств математического ожидания:
- •Искомая дисперсия
- •Пример 1.35. Найти дисперсию ежедневной продажи числа автомашин по данным примера 1.31.
- •Решение. Закон распределения случайной величины X2 имеет вид
- •Математическое ожидание М (X2) подсчитывается из этой таблицы:
- •Математическое ожидание М (X)=2,675. Используя формулу (1.7), получаем искомую дисперсию
- •Рассмотрим свойства функции распределения.
- •Решение. Искомая вероятность
- •Итак, искомая функция распределения
- •Свойства плотности распределения.
- •Вопросы для самопроверки
0 |
при |
x 1. |
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Решение. Искомая вероятность
1
P 0,5 X 1 2 xdx 1 0,25 0,75.
0,5
Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле
x
F(x)= f x dx ,
а, зная функцию распределения, может быть найдена плотность распределения, а именно:
f(x)= F x .
Пример 1.37. Найти функцию распределения по данной плотноcти распределения:
|
0 |
при |
x a , |
f(x)= |
1/(b-a) |
при |
0 x b , |
|
0 |
при |
x b . |
|
|
|
|
Воспользуемся формулой F(x)= |
f x dx . Если x a , |
||
f(x)=0, следовательно, F(x)=0. Если 0 x b , то f(x)= 1/(b-a),
|
|
a |
x |
1 |
|
|
x a |
|
|
следовательно, F(x)= f x |
dx = |
0dx |
|
dx = |
. |
||||
|
|
a b a |
|
|
b a |
||||
0 |
b |
dx |
x |
|
|
b a |
1. |
||
Если x>b, то F(x)= 0dx + |
|
+ 0dx = |
|
|
|||||
|
|
|
|||||||
|
a b a |
b |
|
|
b a |
|
|
||
Итак, искомая функция распределения
50
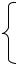
|
0 |
при |
x a , |
F (x)= |
(x-a)/(b-a) |
при |
a x b , |
|
1 |
при |
x b . |
Свойства плотности распределения.
Свойство 1. Плотность распределения – неотрицательная функция:
f(x) 0 .
Свойство 2. Несобственный интеграл от плотности распределения в пределах от до равен единице:
f x dx =1.
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.
В частности, если все возможные значения случайной величины принадлежат интервалу (a,b), то
b
f x dx =1.
a
1.22.8. Числовые характеристики непрерывных случайных величин
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл
51

b
М(х)= xf x dx .
a
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [a,b], то
b
D x [x M X ]2 f x dx.
a
Среднее квадратическое отклонение непрерывной слу-
чайной величины определяется, как и для величины дискретной
X 
 D X .
D X .
1.22.9. Нормальное распределение
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
|
|
1 |
2 |
2 |
|
||
f x |
|
|
|
|
e x a / 2 |
|
. |
|
|
|
|
|
|||
|
|
2 |
|
||||
|
|
|
|
|
|
||
Здесь a - математическое ожидание, - среднее квадратическое отклонение нормального распределения. Достаточно знать эти два параметра, чтобы задать нормальное распределение.
График плотности нормального распределения называют
нормальной кривой (кривой Гаусса) (рис. 2, 3). Изменение ве-
личины параметра а (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль
оси Ох: вправо, если а возрастает, и влево, если а убывает. С возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох; при убывании нормальная кривая становится
52
более «островершинной» и растягивается в положительном
|
f(x) |
f(x) |
1 |
|
|
|
|
|
7,5 |
|
0 |
a |
x |
3 |
x |
|
0 |
|||||
|
|
|
Рис. 2 |
Рис. 3 |
|
направлении оси Оу (рис. 3).
1.22.10. Вероятность попадания в заданный интервал нормальной случайной величины
Как было сказано ранее, если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее интервалу , , такова:
P X f x dx .
Пусть случайная величина Х распределена по нормальному закону. Тогда вероятность того, что Х примет значение, принадлежащее интервалу , , равна
|
|
1 |
|
|
2 |
2 |
|
|
P X |
|
|
|
|
e x a / 2 |
|
dx . |
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
||
Преобразовав эту формулу так, чтобы можно было пользоваться готовыми таблицами, окончательно получаем формулу для вычисления вероятности того, что непрерывная случайная величина, распределенная по нормальному закону, примет
53
значение, принадлежащее интервалу ,
|
a |
|
a |
|
|||
P X Ф |
|
|
- Ф |
|
, |
(1.8) |
|
|
|
||||||
|
|
|
|
|
|||
где Ф(х) – функция Лапласа (1.8).
Пример 1.38. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).
Решение. Воспользуемся формулой (1.8). По условию,10, 50, a 30, 10, следовательно,
|
50 30 |
10 30 |
|
|||
P 10 X 50 Ф |
|
|
- Ф |
|
|
=2Ф(2). |
|
|
|
||||
|
10 |
|
10 |
|
|
|
По таблице находим Ф(2)=0,4772. Отсюда, искомая вероятность
P 10 X 50 2 0,4772 0,9544.
Если распределение изучаемой случайной величины неизвестно, то можно использовать правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. Если это условие выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
54
