§7. Производные и дифференциалы высших порядков

1. Частные производные высших порядков

Пусть функция z =f(x,y) задана на области G. Пусть на G существуют частные производные и. Они называютсячастными производными первого порядка функции f . Эти производные на G являются функциями от x и y: ,. Они тоже могут иметь частные производныеG. Частные производные этих функций φ и ψ называются частными производными второго порядка функции f:

,

,

,

.

Частные производные ивзяты по различным переменным, они называютсясмешанными. Если частные производные второго порядка определены на G, то они сами являются функциями от x и y и могут иметь частные производные по этим переменным. Частные производные от частных производных второго порядка называются частными производными третьего порядка функции f и обозначаются:

(8 штук, 6 смешанных).

Аналогично определяются частные производные и более высоких порядков. Если известны частные производные (n-1)-го порядка, то частные производные от этих частных производных называются частными производными п-го порядка и обозначаются:

Т.о., частные производные высших порядков определяются индуктивно, т.е. последовательно, начиная от первой.

Частные производные ивзяты по одним и тем же переменным, но в разном порядке. Они не обязательно равны!

Теорема 1. Пусть функция z =f(x,y) и ее частные производные определены в некоторой окрестности точки (х₀;у₀), и в этой точке инепрерывны. Тогда.

Доказательство (на оценку отлично).

Придадим значениямх₀ и у₀ приращения Δх и Δу так, чтобы точка (х₀+Δх;у₀+Δу) находилась в окрестности точки (х₀;у₀). Составим выражение

.

Чтобы легче запомнить, как строится выражение, рассмотрим прямоугольникАBСD с вершинами А(х₀+Δх;у₀+Δу), B(х₀+Δх;у₀), С(х₀;у₀), D(х₀;у₀+Δу). Тогда числитель равен алгебраической сумме значений функции f(x,y) в вершинах прямоугольника, причем значение в точке А берется со знаком «+», и при обходе прямоугольника против часовой стрелки знаки перед остальными слагаемыми чередуются.

Введем вспомогательную функцию

.

Здесь числитель равен разности значений функции f(x,y) в точках сторон АD и ВС с одинаковыми абсциссами. Тогда ω можно записать в виде:

=

.

По условию существует , значит, существует и

.

Т.к. функция φ(х) дифференцируема на отрезке [x₀;x₀+Δx], то она непрерывна на этом отрезке. Следовательно, к ней можно применить формулу Лагранжа:

=, где. (1)

Т.к. по условию существует и , то к функции, как к функции оту, на отрезке [у₀;у₀+Δу] можно тоже применить формулу Лагранжа:

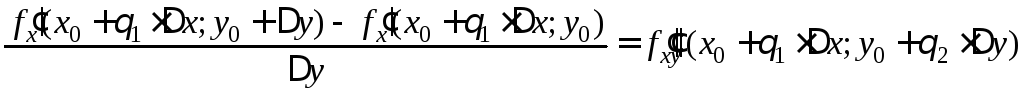, (2)

где . Тогда из (1) и (2) следует

, где . (3)

Теперь вместо функции φ(х) рассмотрим функцию

.

Тогда

=

.

Применим формулу Лагранжа к функции ψ(у)на отрезке [у₀;у₀+Δу]:

,

а затем к функции , как к функции отх, на отрезке [x₀;x₀+Δx]:

, где . (4)

Из соотношений (3), (4) следует

. (5)

Пусть . Тогда

, .

Т.к. по условию инепрерывны в точке (х₀;у₀), то

и

.

Тогда, переходя в равенстве (5) к пределу при , получим

.

Замечание. Утверждение, аналогичное теореме 1, может быть доказано и для смешанных производных любого порядка. Т.е. смешанные производные любого порядка при условии их непрерывности не зависят от порядка дифференцирования, например,

.

Теорема 2. Если смешанные производные n – го порядка, отличающиеся только порядком дифференцирования, непрерывны на области G, то они на этой области равны.