Advanced_Renderman_Book[torrents.ru]

100 4 Geometric Primitives

Figure 4.3 Examples of each of the four types of polygonal primitives.

convex, the renderer will probably draw it incorrectly (filling in holes or concavities, for example).

RenderMan also provides two packaging styles-individual polygons and polyhedra. Polyhedra are sets of polygons that share vertices, which makes for efficient database description because defining each such polygon individually would require large numbers of redundant vertex descriptions to be passed through. Polyhedra are described by first specifying all of the vertices and then specifying which vertices are linked together in which order to create each individual polyhedral face. Figure 4.3 shows examples of various types of polygonal primitives.

Polygons do not have a specific parameter that holds the positions of each vertex. Instead, every polygon primitive has a parameter list, which contains the vertex data. The primitive variable "P" denotes vertex information, an array of floatingpoint numbers that are the 3D vertex coordinates. For example, a triangle would have a "P" array with nine floating-point numbers.

Section 4.1 discussed the fact that additional data, known as primitive variables, can be attached to the vertices of polygons and other primitives. For every polygon type, primitive variables of type "vertex" and "varying" occur with the same frequency-one per polygon vertex. Primitive variables of type "uniform" happen once per facet-that is, exactly once on individual polygons and once per polyhedral face on polyhedra. Naturally, primitive variables of type "constant" appear exactly once regardless of primitive type.

The single onus that the other parameter list values can place on the geometric description of polygonal primitives concerns vertex uniqueness. A vertex is "shared" in a polygon only if all of the values associated with that vertex are identical. If a vertex has to have two different values for any parameter (say, color), depending on which of two faces it is part of, then those two faces don't actually

share a common vertex, but have "different but coincident" vertices, and those vertices must be specified separately.

Polygon parameterlist

Polygon creates an individual convex polygon, with any number of vertices.

General Polygon loopverts parameterlist

General Polygon creates an individual concave polygon (or polygon with holes). The parameter loopverts is an array of integers that specifies how many vertices make up each loop of the general polygon. General polygons that are concave but have no holes would have just one loop, so the loopverts array would have one entry.

PointsPolygons nverts vertids parameterlist

Poi ntsPol ygons creates a polyhedron made up of many convex polygons. The parameter nverts is an array of integers that specifies how many vertices make up each polyhedral face. For example, a cube would have six entries, all saying 4.

The parameter vertids is a long array of integers that specifies the index number of the vertices that make up the edges of each of the faces. Its length is equal to the sum of all the entries in the nverts array. In the cube example, it would have 24 entries, the first four listing the vertices in order for the top face, then four listing the vertices for a side, and so on. Vertex indices start at 0, which specifies the first vertex in the "P" array.

nloops loopverts vertids parameterlist

Poi ntsGeneral Polygons is the most complex and confusing of the four polygon calls because it is the superset of all of them. It creates a polyhedron made up of many general polygons, each with potentially several loops describing its holes. The parameter nloops is an array of integers that describes, for each general polygon face of the polyhedron, how many loops that face has. It is not uncommon for this array to be all 1 s, specifying a polyhedron made of concave polygons that have no holes. The parameter loopverts is an array of integers that describes how many vertices are in each loop. Its length is obviously the sum of all the values in nloops.

Notice that for the two polyhedron primitives, the indirection provided by the vertex indices means that the order of the vertices in the "P" array is not critical. In fact, even the number of values in the "P" array is not critical. If some vertices are not referenced, there is no harm done, just a little database inefficiency.

102 4 Geometric Primitives

4.4Parametric Patches

The workhorse primitives of most RenderMan scenes are the parametric patch primitives. These primitives are topologically rectangular (they have four sides), and the two pairs of opposite sides are called their parametric directions, denoted a and v. Patches are curved, so they are useful in photorealistic renderings where they need to be seen at a wide range of sizes with no polygonal approximation artifacts. They can be connected with smooth continuity, so they are useful for approximating other primitives that RenderMan does not support directly, such as surfaces of revolution. They have easy-to-understand rectangular parametric spaces, so they are relatively intuitive to texture map.

Although there is a large set of potential choices for patch primitives, RenderMan has chosen three relatively general primitives that span a large range of functionality: bilinear patches, bicubic patches, and non-uniform rational B-splines (NURBS, discussed in the next section). Bilinear patches are quadrilaterals, where each edge is a straight line, but the patch is a smooth curved surface that connects the edges. It is an example of a ruled surface, so named because it can be created by sweeping a straight-edged "ruler." The set of points on the surface with one parametric coordinate identical is always a straight line.

Bicubic patches have cubic curves on each edge. Cubic curves can be characterized by their basis function. Cubic basis functions are equations that determine the shape of the curve, using four control points as parameters. Geometrically, some basis functions use their control points as locations; others use their control points as tangent directions. There is a wide variety of cubic basis functions available (Farin, 1990), each customized to manipulating the curve in a particular way. RenderMan has several common basis functions built in and also provides the capability for the modeler to define its own basis function.

As with polygons, the vertex (also called control point) information is passed in an array in the parameter list. Patches can take two types of control-point data: standard 3D vertices, denoted by "P"; and rational or homogeneous 4D vertices, denoted by "Pw". This control-point information is used according to the basis function of the patch.

Basis specifies the two cubic basis functions (one for each parameteric direction) that will be used to create bicubic Patch and PatchMesh primitives.

The and vbasis parameters can be either a string, identifying one of the standard built-in basis functions, or can be a 16-element floating-point array, specifying the basis function in matrix notation. RenderMan's built-in set of basis

functions include "bezier", "bspline", "catmull-rom", and "hermite".

Every cubic basis function has a step value associated with it for use by the Patch mesh primitive. It specifies how many control points should be skipped to go from the first patch in a mesh to the second patch in the mesh, and

Basis ubasis ustep vbasis vstep

103

4.4Parametric Patches

so on. The required basis steps for the standard bases are: three for Bezier, two for Hermite, and one for B-spline and Catmull-Rom. This means, for example, that a patch mesh with two Bezier patches in the a direction would have seven control points in that direction. A patch mesh with two B-spline patches would have only five control points in that direction. The designers of other basis matrices must determine the appropriate step value based on themathematical details of the particular matrices.

Patch type parameterlist

Patch defines an individual parametric patch primitive. If type is "bi1inear", the 2 x 2 control points define a bilinear patch. If type is "bicubic", the 4 x 4 control points define a bicubic patch, according to the basis functions specified by the preceding Basis call. The 16 control points are specified in row-major order; that is, the point at (u, v) = (0, 0) first, (1, 0) fourth, (0, 0.25) fifth, and (1, 1) last.

Patch Mesh type nu uwrap nv vwrap parameterlist

Patch Mesh creates a rectangular mesh of patches. Like a polyhedron, the patch mesh is more compact than a series of patches because it shares vertices. Patch meshes can be "bilinear" or "bi cubic" depending on their type. Nu and nv specify the number of control points in the a and v directions, respec tively. Bicubic meshes use the basis functions and basis step values specified by the preceding Basis call, so the number of control points must be appro priate according to those values.

In addition, patch meshes can wrap. This means that they are connected to gether in one parametric direction or another, creating a cylinder, or even in both, creating a torus. This means that the mesh uses some control points from the "end of the line" followed by some control points from the "begin ning of the line" to create a patch that connects the end to the beginning. If the uwrap or vwrap parameters are "periodic", they have this behavior in the respective parametric direction. If they are "nonperi odic", they do not.

When specifying primitive variables on bilinear or bicubic patches, variables of type "vertex" have the same frequency as the control points, 4 on bilinear and 16 on bicubic patches. Primitive variables of type "varying" occur at the parametric corners, so require 4 values on any patch. Primitive variables of type "uniform" or "constant" occur exactly once on a patch.

The situation with patch meshes is a bit more complex, for two reasons. First, there are many interior parametric corners (at the edges of each individual patch in the mesh). Second, the wrapping behavior determines the number of patches that the mesh has in each parametric direction. Because "uniform" variables occur once per patch, and "varyi ng" variables occur once per parametric corner, the equations for computing the appropriate numbers for a given patch mesh are somewhat

4 Geometric Primitives

104

10 x 7 aperiodic Bezier bicubic patch mesh

3 x 2 subpatches

4 x 3 varying variable positions

9 x 5 U-periodic Catmull-Rom bicubic patch mesh 9 x 2 subpatches

9 x 3 varying variable positions

Figure 4.4 Typical patch mesh primitives.

complex. However, as Figure 4.4 shows, it is not that difficult to understand the intent. The number of patches, and the number of varying data items, in the u parametric direction is

And similarly for the v direction. So the total number of data values on the whole mesh for variables of type "vertex" is nu - nv. The number of data values for variables of type "varying" is nuvarying - nvvarying. The number of data values for variables of type "uniform" is nupatches - nvpatches. There is always exactly one data value for any variable of type "constant".

4.5 NURBS

The most general type of parametric patch, and certainly the most complex, is the NuPatch, RenderMan's version of the nonuniform rational B-spline patch or NURBS patch.*2 A nu-patch is similar to a patch mesh, in that it has parametric curves in each direction, which create a rectangular array of individual subpatches. However, the mathematical equations that generate nu-patches are generalized over standard patches to give more descriptive power and more detailed control of the shape of the primitive.

4.5.1NURBS Curves

Like B-spline curves, NURBS curves are parametric curves that are specified with control points. The NURBS curves are divided into segments, with each segment defined by a few of the control points. The control points overlap with a "step" of one, meaning that adding one more control point to the list adds one more segment to the curve.

The differentiating characteristic of a NURBS curve is the knot vector. The knot vector is a nondecreasing series of numbers that controls the basis functions of the curve, just as the basis matrix did for the cubic curves described previously. The basis functions determine how much importance each of the control points has in specifying the position of the curve. For example, in a Bezier cubic curve, the curve passes through the first and fourth control point, whereas in a B-spline cubic curve the curve only passes near them. In addition, the knot vector also controls the parameterization of the curve, so curves that are geometrically identical can have different parametric coordinates. For example, three typical knot vectors might be

In the use of NURBS curves, one type of knot vector stands out as particularly interesting. Any knot vector that is an increasing series of integers is known as a uniform knot vector. It is notable because NURBS curves that use a uniform knot vector are the standard B-spline-basis curves with which we are already familiar. Various other special forms of knot vectors are of interest as well, because the knot vector can create the other familiar basis functions such as Bezier basis. The more complex nonuniform knot vectors, from whence the NURBS gets its name,

*2 The word NURBS is commonly used as a singular adjective and as a plural noun-"a NURBS curve" versus "NURBS are confusing."

106 4 Geometric Primitives

generalize the basis functions so that individual control points can have Bezierlike qualities, or B-spline-like qualities, or various other styles, all within the same curve.

It turns out that the values in the knot vector can be uniformly offset or scaled without changing the curve geometrically. The only change in the curve is that the parametric coordinates of every point on the curve will be offset or scaled by the same amount. This means that a knot vector that is an increasing series of multiples of any number is uniform, too. We can use this feature to reparameterize a curve that used to run from u = 0 to u = 5 into a curve that runs from u = -1 to u = 1, if that turns out to be useful for any reason.

The second generalization of the NURBS curve over a standard cubic curve is the degree of the curve. The degree refers to the polynomial complexity of the curve's equation. A cubic curve, by definition, has degree three. This means that the equation for the curve includes a u3 term somewhere and that this is the highest power of a that appears. A linear curve has degree one. RenderMan's NURBS curve can have any degree desired, so, for example, creating quadratic curves or quartic curves is easy.

Actually though, in RenderMan, we specify curves by their order, which is just the degree plus 1-cubic curves are order 4. There is no additional complexity, no subtle cases, it's just a terminology thing. The order identifies how many control points it takes to make one segment. A cubic curve requires four control points. It also identifies how many knots are necessary to make a segment, that being 2 - order. As mentioned earlier, adding a segment to a NURBS curve requires adding one control vertex, and it also requires adding one knot. Therefore, the number of knots required to specify a curve is new + order.

A key factor in the way that knot values are interpreted is called the multiplicity of the knot. In any nondecreasing knot sequence, several knots in a row might have the same value. This causes discontinuities in the curve description. A NURBS curve is continuous at its normal knot values (e.g., a cubic NURBS curve is continuous at normal knots). If a knot value appears twice (doubled, or multiplicity 2), then one level of continuity vanishes, and a tripled knot makes two levels of continuity vanish. 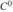A cubic curve is onlyat doubled knots and(has a cusp) at tripled knots.

The final component of the name NURBS is rational. This means that the control points of the NURBS curve are homogeneous points, with four components. As with other homogeneous coordinate mathematics in computer graphics, this means that the parametric equations create functions to compute x, y, z, and the homogeneous coordinate iv, and that at any place in the geometric pipeline when true 3D positions are required, x, y, and z are each divided by 1v to get those values. If the homogeneous coordinates of all of the control points are 1, the curve is called polynomial, and the vv components of all of the other calculations are also 1. This means we can obviously ignore the vv divide and can actually ignore the w component entirely. In RenderMan, nu-patches, standard patches, and patch meshes can

107

4.5NURBS

all have rational homogeneous coordinates for their control points, which is why we don't single out nu-patches as "nur-patches."

4.5.2NURBS Patches

RenderMan's nu-patches (NURBS) are relatively standard as far as CAD/CAE geo metric modeling descriptions go. They are based on the NURBS support of PHIGS+, which in turn is extremely similar to those in IGES and STEP, the main international standards for NURBS.

Nu-patches can be any order in the a and v parametric directions, not necessarily the same, and any uniform or nonuniform knot vector is acceptable. Some packages enforce limits on the multiplicity of knots, because it makes little sense to have knot multiplicity greater than the order, but RenderMan doesn't enforce that particular restriction (it just skips the empty disconnected sections). Nu-patches can also specify parametric clipping values, which allows the ends of the nu-patch to be trimmed off without having to remodel it. It is unclear why this is important, but we just go along with it.

Nu Patch nucv uorder uknot umin umax nvcvs vorder vknot vmin vmax

The NuPatch call creates a nu-patch (also known as a NURBS patch). There are five parameters that control each parametric direction of the nu-patch: the parameters nucvs and nvcvs are integers that identify the number of control points in each direction; uorder and vorder are integers that specify the order of the NURBS curves in each direction; uknot and vknot are the floating-point arrays that contain the knot vectors in each parametric direction. The knot vectors must obey the standard rules of being nondecreasing sequences, and each is new + order in length. The parameters min and max clip the nu

patch to the parametric range [min, max] in each parametric direction. The math requires that this range not extend outside of the range knot[order-1] to knot[ncvs].

For specifying primitive variables, nu-patches are handled as though they were nonperiodic B-spline patch meshes. Recall that the number of segments in each NURBS curve is ncvs - order + 1. Multiplying values for the two parametric curves together gets the number of "subpatches" in the nu-patch. For primitive variables of class "vertex", there are nucvs - nvcvs data items. For primitive variables of class "varying", there is one data value per segment corner, which is (nusegments + 1) (nvsegments + 1) values. For primitive variables of class "uniform", there is one data value per segment, or nusegments - nvsegments values. For primitive variables of class "constant", there is exactly one data value.

108 4 Geometric Primitives

Two good books for understanding the details of NURBS are Piegl and Tiller's The NURBS Book and Farm's NURB Curves and Surfaces. In the terminology of Piegl's book, our ncvs is n + 1, order is p + 1, and nknots is m+1.

4.5.3Trim Curves

RenderMan supports trim curves, which are NURBS curves drawn in the parameter space of a nu-patch, which "cuts a hole" in the surface. This is typically used for "trimming" the edges of the patch so that it doesn't have a rectangular shape but still maintains a rectangular parametric coordinate system (for the convenience of texturing and other parametric operations). One example of this is when two NURBS patches intersect to form a joint. It is rarely the case that they join at a nice clean isoparametric line on both of the patches. Instead, each NURBS patch is trimmed at the line of intersection. Notice that trim curves are defined in the parameter space of the patch, not in 3D. This make some uses of trim curves more convenient and makes other uses more difficult. Trim curves operate only on NuPatch primitives. If quadrics, patch meshes, or other primitives need to be trimmed, they must first be reformulated as nu-patches.

Trim curves resemble General Polygons in the way that they are defined. The trim "curve" is actually a set of loops, and each loop is a series of NURBS edge curves, connected head-to-tail, which must be explicitly closed (e.g., by repeating vertices). A trimming loop draws a line on the surface.

The RenderMan Interface Specification says that the part of the surface that is "kept" and the part that is "thrown away" are dependent on the direction that the loop is wound. But both PRMan and BMRT simply perform a "crossing" test, without regard to the actual

directions of the loops. The inside or outside of the trim region to be kept or thrown away

can be selected with Attribute "trimcurve" ["inside"] or Attribute "trimcurve"

["outside"]. The default is "inside", indicating that the renderer should keep the part of the patch on the inside of the trim curve and throw away the part of the patch on the outside of the trim curve (obviously, "outside" keeps the outside and throws away the inside of the trim region).

Trim curves are attributes in the hierarchical graphics state. This means that multiple nu-patch primitives can be trimmed with the same curve-for example, if it is valuable to rubber-stamp a large number of identically shaped items. Removing the trim curve from the state can be done by AttributeEnd, or by specifying a new TrimCurve with 0 loops.

TrimCurve nloops ncurves order knot min max n u v w

The TrimCurve call specifies the multiple loops that will trim nu-patch primitives. The integer parameter nloops specifies the number of loops that will cut the primitive. Each loop is made up of multiple edge curves, specified in the integer array ncurves. The order and number of knots in each edge curve are specified in the integer arrays order and n, respectively. The knots them

selves are specified in the floating-point array knots. The knot values for all the edges are concatenated into one long array. Each edge curve can be clipped to a particular parametric range with the floating-point min and max arrays.

For reasons that are lost in time, trim curve control points are not specified with the standard parameter list syntax that every other primitive uses. In stead, the homogeneous u, v, and w coordinates of the trim curve control points are specified in individual floating-point arrays.

4.6Subdivision Meshes

Perhaps the most interesting new primitive that has been added to the RenderMan family is subdivision mesh (also called "subdivision surface"). The great motivation for using subdivision meshes is that they simultaneously capture the most desirable properties of several of the different surface types that we currently use. A subdi vision mesh, as with patch primitives, is described by its mesh of control points. The surface itself interpolates this mesh and is piecewise smooth. However, unlike NURBS or patch mesh primitives, its mesh is not constrained to be rectangular, a major limitation of parametric patches. It can have arbitrary topology and arbitrary vertex valence. In this respect, the mesh is analogous to a polyhedral description. No longer do you have to painstakingly model a smooth surface as a quilt of rec tangular patches.

But where a polyhedral surface requires a large number of data points to approx imate a smooth surface, a subdivision mesh is always smooth and needs far fewer points to produce the same quality of smooth surface fit (see Figure 4.5). This sig nificantly reduces the time necessary to create the model, reduces the amount of data necessary to hold the model, and gives the model significantly more flexibility in terms of the range of model distances and image resolutions at which the model will look good. There is no point at which the rendering of the model betrays its underlying polygonal basis.

For animation, the subdivision surface also shares another important feature with polyhedra: adding detail is a local operation. There is no need to add large "isoparams" that extend far beyond the area of interest. And because there are no topology restrictions, edges can follow character features (such as skin folds) more directly. This leads to better isolation of one part of the mesh from another, such as when model articulation requires "muscles" that drag vertices along lines that traverse the surface in arbitrary directions. Adding vertices to the mesh along these lines leads to fewer problems with unintentional muscle effects on distant parts of the surface.

The RenderMan API for subdivision meshes is extremely powerful and permits the specification of variable sharpness creases along a surface, holes, and other enhancements as described in recent literature (DeRose, Kass, and Truong, 1998).