Сравнительное исследование эффективности методов

В этом параграфе проводится сравнительное исследование поисковых методов минимизации мультимодальной функции одной переменной на основе схем отбора интервалов, метода последовательного перебора, монотонного алгоритма глобального поиска Стронгина и метода ломаных. В качестве параметра эффективности метода выберем количество вычисления значений функций для достижения заданной точности.

Подобный метод определения эффективности численных методов используется многими другими авторами, например Стронгиным [17]. В таблицах 4-9 представлены результаты вычисления этого параметра эффективности для перечисленных методов. Результаты для метода ломаных и поискового метода на основе трехзвенной схемы отбора интервалов первого порядка были взяты из работы [9]. Результаты для монотонного алгоритма глобального поиска Стронгина и поискового метода на основе трёхзвенной схемы отбора интервалов второго порядка были взяты из работы [14]. Под точностью будем понимать абсолютную погрешность значения точки глобального минимума , где- точное значение точки глобального минимума, - приближенное значение точки глобального минимума, вычисленное с помощью программы.Для достижения нужной точности используется параметр, который есть в каждом методе и при устремлении его к нулю, заданная точность должна быть достигнута. Для всех поисковых методов, метода последовательного перебора, метода ломаных и монотонного алгоритма глобального поиска Стронгина таким параметром является - оценка погрешности приближенного значения точки глобального минимума. Этот параметр используется и вводится непосредственно в программе. Т.о. при его последовательном уменьшении абсолютная погрешность точки глобального минимума также будет уменьшаться.

В первой колонке задается значение , такое чтои приблизительно равное . Фиксируем значениеи уменьшаем значение параметра соответствующего метода до тех пор, пока значение погрешности не станет меньше или равными в то же время близким к. Для последнего случая фиксируем количество вычислений значения функции и помещаем его в таблицу.

Для некоторых задач точное значение глобального минимума аналитически найти невозможно. В этих случаях это значение находится с помощью численного метода. Для получения значения параметра воспользуемся поисковым методом на основе двухзвенной схемы отбора интервалов первого порядка. С его помощью найдем значение точки глобального минимума с высокой точностью, т.е. при. Полученное значение используем как точное значение точки глобального минимума исследуемой функции при вычислении погрешности.

Характерной особенностью всех методов, кроме поисковых, является использование в качестве исходного данного константы Липшица для функции на.В простейших случаях константа Липшица вычисляется аналитически. Аналитический метод вычисления константы Липшица заключается в том, что находится производная функции и вычисляется ее максимум на том отрезке, для которого ищется минимум функции. Таким образом, на отрезке вычисляется производная исследуемой функции равное . Константа Липшица выбирается равной.Часто константу Липшица аналитически вычислить очень сложно, например, если исследуемая функция не является элементарной или если метод одномерной минимизации используется в качестве вспомогательного метода в решении задач много мерной минимизации. Поэтому методы, использующие ее для своих вычислений, сопровождаются дополнительной программой вычисления константы Липшица.

Вычисление константы Липшица обычно производится сеточным методом. На отрезке строится сетка източек, таким образом получена последовательность точек, где,,. Затем производится вычисление значений- значения функции в точках ,.

Обычно заранее невозможно определить значение при котором будет достаточно близка к значению. Поэтому для получения приближенного значенияс заданной точностьюиспользуется итерационный процесс.

Зададим последовательность для каждой пары вычисляются значенияи.Вычисляем, где- значения функции в соседних узлах сетки. Затем вычисляем значение, где и сравниваем по модулю разность значений и. Еслименьше заданного некоторого, то константа Липшица считается найденной и равной с погрешностью , иначе удваиваем значениеи вычисляем новые значенияи. Погрешность значениязависит от значенияи припогрешность.

Данный метод можно оптимизировать, если вместо использовать. Данная оптимизация ускоряет вычисление константы Липшица ви более раз, но при этом необходимо отдельно рассмотреть случай, при которомЭто происходит в том случае, если функция является постоянной (константой), в этом случае значение константы Липшица берется равным.

В случае программного поиска константы Липшица общее количество вычислений функции является суммой значений количества вычислений функции, необходимого для получения константы Липшица и количества вычислений функции, необходимого для нахождения приближенного значения точки глобального минимума одним из методов, использующих константу Липшица.

Если константа Липшица вычисляется аналитически, трудоемкость методов будет существенно разной, поэтому все выводы делаются в каждом случае отдельно.

В таблицах 4-9 используются следующие обозначения:

- заданная точность искомого приближенного значения точки глобального минимума;

sL - Число вычислений функции для определения константы Липшица, найденное при определении константы Липшица сеточным методом;

sML1 – Число вычислений функции для метода ломаных с вычисленной константой Липшица;

sML2 – Число вычислений функции для метода ломаных с найденной константой Липшица используя максимум производной функции;

sSL1 – Число вычислений функции для АГП (алгоритм глобального поиска) Стронгина с вычисленной константой Липшица;

sSL2 – Число вычислений функции для АГП Стронгина с найденной константой Липшица используя максимум производной функции;

sPL1 – Число вычислений функции для метода последовательного перебора с вычисленной константой Липшица;

sPL2 – Число вычислений функции для метода последовательного перебора с найденной константой Липшица используя максимум производной функции;

s3z1 – Число вычислений функции для метода на основе трёхзвенной схемы отбора интервалов первого порядка;

s3z2 – Число вычислений функции для метода на основе трёхзвенной схемы отбора интервалов второго порядка;

s2z1 – Число вычислений функции для метода на основе двухзвенной схемы отбора интервалов первого порядка.

Модельная задача 1. Ищется минимум функции на отрезке (рис. 4). Вычисленное значение константы Липшица = 35452. Точное значение точки минимума функции = 1,54978592608382.

Рис 4. График функции

Функция характеризуется большим количеством узких локальных минимумов. Данная модельная задача проверяет эффективность работы исследуемых методов в случаях, когда функция имеет множество локальных минимумов одинаковой ширины, один из которых является глобальным.

Таблица 4

	sL	sML1	sML2	sSL1	sSL2
10-2	1048574	64	64	190	190
10-3	1048574	512	512	6767	8765
10-4	1048574	8192	8192	39111	59181
10-5	1048574	19146	34451	611564	1110472
10-6	1048574	30797	63900	640772	1329008

Таблица 5

	sPL1	sPL2	s3z1	s3z2	s2z1
10-2	2120	2120	282	83	964
10-3	6060	6060	2053	2707	9096
10-4	78257	78257	13684	6629	13264
10-5	733560	733560	29796	160938	146712
10-6	961392	1613920	53814	237323	358651

Выводы по модельной задаче 1.

1. В случае, когда константа Липшица найдена программно сеточным методом, лучший результат при оценках погрешности 10^-2 и 10^-4 показал поисковый метод на основе трехзвенного отбора интервалов второго порядка, при оценках погрешности 10^-3, 10^-5 и 10^-6 лучший результат показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат при оценках погрешности 10^-2, 10^-4 и 10^-6 показал метод последовательного перебора, при оценках погрешности 10^-3 и 10^-5худший результат показал метод АГП Стронгина.

2. В случае, когда константа Липшица найдена аналитически, лучший результат при оценках погрешности 10^-2 и 10^-3показал метод ломаных, при оценке погрешности 10^-4 лучший результат показал поисковый метод на основе трехзвенного отбора интервалов второго порядка, при оценках погрешности 10^-5 и 10^-6 лучший результат показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат при оценках погрешности 10^-2, 10^-4 и 10^-6 показал метод последовательного перебора, при оценках погрешности 10^-3 и 10^-5 худший результат показал метод АГП Стронгина.

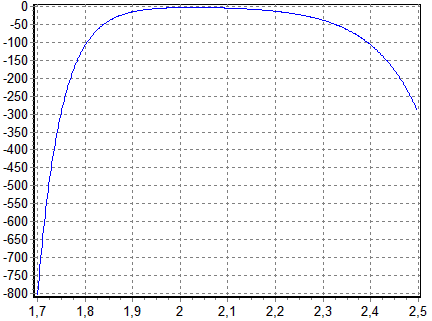
Модельная задача 2. Ищется минимум функции на отрезке (рис. 5).

Вычисленное значение константы Липшица = 1603. Точное значение точки минимума функции = 1,7.

Рис 5. График функции

Функция характеризуется двумя минимумами на краях. Данная модельная задача проверяет эффективность работы исследуемых методов в случае, когда функция имеет только 2 минимума, которые расположены на краях отрезка.

Таблица 6

	sL	sML1	sML2	sSL1	sSL2	sPL1	sPL2	s3z1	s3z2	s2z1
10-2	2046	18	48	21	56	39	170	84	89	228
10-3	2046	21	71	23	69	44	180	91	91	231
10-4	2046	21	82	25	85	48	189	93	93	233
10-5	2046	23	91	23	93	57	226	94	94	233
10-6	2046	24	102	26	107	60	253	94	94	233

Выводы по модельной задаче 2:

1. В случае, когда константа Липшица найдена программно сеточным методом, лучший результат при всех значениях оценки погрешности от 10^-2 до 10^-6 показал поисковый метод на основе трехзвенного отбора интервалов первого порядка, который примерно равен результату поискового метода на основе трехзвенного отбора интервалов второго порядка. Худший результат при всех значениях оценки погрешности показал метод последовательного перебора.

2. В случае, когда константа Липшица найдена аналитически, близкие результаты показали методы ломаных и АГП Стронгина, которые являются лучшими. Худший результат при значениях оценки погрешности от 10^-2 до 10^-5 показал поисковый метод на основе двухзвенного отбора интервалов первого порядка, при значении оценки погрешности 10^-6 худший результат показал метод последовательного перебора.

Модельная задача 3. Ищется минимум функции на отрезке (рис. 6). Вычисленное значение константы Липшица =66.Точное значение точки минимума функции =-2,80248519396926.

_{Рис 6. График функции}

_{Функция характеризуется большим количеством локальных минимумов и четна. Данная модельная задача проверяет эффективность исследуемых методов в случае, когда функция имеет несколько локальных минимумов разной ширины и несколько глобальных минимумов.}

Таблица 7

	sL	sML1	sML2	sSL1	sSL2	sPL1	sPL2	s3z1	s3z2	s2z1
10-2	8190	300	504	354	619	380	640	234	295	295
10-3	8190	624	1344	862	1909	1684	3621	427	616	1159
10-4	8190	1236	2400	1368	2658	2729	5295	704	731	1541
10-5	8190	3255	5432	1973	3289	5108	8531	704	738	1877
10-6	8190	8080	12468	3025	4649	9232	14218	704	782	2218

_{Выводы по модельной задаче 3.}

_{1. В случае, когда константа Липшица найдена программно сеточным методом, лучший результат при всех значениях оценки погрешности показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат при всех значениях оценки погрешности показал метод последовательного перебора.}

2. В случае, когда константа Липшица найдена аналитически, лучший результат при всех значениях оценки погрешности показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат при всех значениях оценки погрешности показал метод последовательного перебора.

_{Модельная задача 4. Ищется минимум функции на отрезке [1;2] (рис 8). Точное значение точки минимума функции = 1,88404514910365. Так как значение константы Липшица программно вычислить не удалось, использовалось значение, полученное в результате оценки максимума модуля производной функции, это значение равно 1.}

_{Рис 7. График функции.}

_{Функция характеризуется очень большим количеством узких и низких локальных минимумов (минимум функции на этом отрезке ~ 4,5*10-8). Для нее не удалось вычислить константу Липшица ввиду высокой сложности функции, использовался только метод с максимумом производной функции на отрезке. Данная модельная задача проверяет эффективность работы исследуемых методов в том случае, когда функция имеет множество узких и низких локальных минимумов разной ширины, каждый из которых близок к нулю.}

Таблица 8

	sL	sML1	sML2	sSL1	sSL2
10-2	Нет рез.	Нет рез.	67	Нет рез.	91
10-3	Нет рез.	Нет рез.	518	Нет рез.	1119
10-4	Нет рез.	Нет рез.	8194	Нет рез.	14622
10-5	Нет рез.	Нет рез.	65536	Нет рез.	106286

_{Таблица 9}

	sPL1	sPL2	s3z1	s3z2	s2z1
10-2	Нет рез.	62	13	18	12
10-3	Нет рез.	423	88	193	72
10-4	Нет рез.	5376	784	1406	552
10-5	Нет рез.	50720	7566	14762	5520

_{Выводы по модельной задаче 4.}

_{1. В случае, когда константа Липшица ищется программно сеточным методов, результат для методов ломаных, АГП Стронгина и последовательного перебора получить не удалось ввиду высокой вычислительной сложности функции. Лучший результат при всех оценках погрешности показал поисковый метод на основе двухзвенного отбора интервалов первого порядка.}

_{2. В случае, когда константа Липшица найдена аналитически, лучший результат при всех оценках погрешности показал поисковый метод на основе двухзвенного отбора интервалов первого порядка. Худший результат при всех оценках погрешности показал метод последовательного перебора.}

_{Общие выводы исследования модельных задач:}

_{1. В случае, когда константа Липшица ищется программно сеточным методом, лучший результат показал поисковый метод на основе трехзвенного отбора интервалов второго порядка для значения оценки погрешности 10-2. Для остальных значений оценки погрешности, лучший результат показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат показал метод последовательного перебора для всех значений оценки погрешности.}

_2. В случае, когда константа Липшица ищется аналитически, лучший результат показал поисковый метод на основе трехзвенного отбора интервалов второго порядка для значения оценки погрешности 10^-2. Для остальных значений оценки погрешности, лучший результат показал поисковый метод на основе трехзвенного отбора интервалов первого порядка. Худший результат показал метод последовательного перебора для всех значений оценки погрешности