
- •Российская Федерация
- •Введение
- •Исследование поискового метода минимизации мультимодальной функции одной переменной на основе двухзвенной схемы отбора интервалов первого порядка Метод последовательного перебора
- •Поисковый метод минимизации мультимодальной функции одной переменной на основе двухзвенной схемы отбора интервалов первого порядка
- •Реализация поискового метода минимизации мультимодальной функции одной переменной на основе двухзвенной схемы отбора интервалов первого порядка и метода последовательного перебора
- •Сравнительное исследование эффективности методов
- •Заключение
- •Список литературы
- •Приложение
Исследование поискового метода минимизации мультимодальной функции одной переменной на основе двухзвенной схемы отбора интервалов первого порядка Метод последовательного перебора
Обозначим
через
 класс функций, удовлетворяющих условию
Липшица на отрезке
класс функций, удовлетворяющих условию
Липшица на отрезке ,
с одной и той же для всех функций этого
класса константой
,
с одной и той же для всех функций этого
класса константой .
Для функции
.
Для функции будем
рассматривать задачу минимизации
первого типа, когда ищется величина
будем
рассматривать задачу минимизации
первого типа, когда ищется величина
 .
.
На
классе
 можно предложить простой и эффективный
последовательный метод перебора, когда
выбор точки
можно предложить простой и эффективный
последовательный метод перебора, когда
выбор точки при каждом
при каждом производится с учетом вычислений
значения функции в предыдущих точках
производится с учетом вычислений
значения функции в предыдущих точках и
задачу: как выбрать число
и
задачу: как выбрать число
 и метод
и метод ,
чтобы
,
чтобы
 (1)
(1)
удается решить за меньшее количество вычислений значений функции. Положим
 (2)
(2)
где
 ,
, ,
,
 ,а
число
,а
число
 определяется условием
определяется условием .
.
Теорема 1.
Метод
последовательного перебора
(2)
решает задачу (1) на классе
 .
.
Описание метода
Пусть
функция
 удовлетворяет условию Липшица на
удовлетворяет условию Липшица на с известной
константой
с известной
константой
 .
Тогда, согласно следствия из теоремы
4.5, будет существовать минимум
.
Тогда, согласно следствия из теоремы
4.5, будет существовать минимум и хотя бы одна из точек минимума
и хотя бы одна из точек минимума функции на
функции на .
Будем искать приближения для минимума
.
Будем искать приближения для минимума и какой-нибудь точки
минимума
и какой-нибудь точки
минимума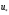 функции
функции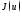 на
на (
( )
с погрешностями, не превышающими
заданного положительного числа
)
с погрешностями, не превышающими
заданного положительного числа .
.
Для
решения поставленной задачи разобьем
 на
на
 отрезков
отрезков
 ,
, ,
, ;
; .
Вычислим значения функции
.
Вычислим значения функции (
( )
в очках разбиения и найдем
)
в очках разбиения и найдем .
Далее сравним полученное значение
.
Далее сравним полученное значение с величиной
с величиной ,
чтобы не выйти за границы отрезка, на
котором ищется минимум функции. Если
выполняется условие
,
чтобы не выйти за границы отрезка, на
котором ищется минимум функции. Если
выполняется условие ,
то переходим к следующему шагу поиска
минимума функции. Как только это условие
,
то переходим к следующему шагу поиска
минимума функции. Как только это условие
 перестанет выполняться, возьмем в
качестве последней проверяемой точки
перестанет выполняться, возьмем в
качестве последней проверяемой точки .После
этого выберем в качестве приближений
для точного значения точки минимума
.После
этого выберем в качестве приближений
для точного значения точки минимума
 и точного значения минимума функции
и точного значения минимума функции значения
значения и
и ,
где значение
,
где значение выбирается соответствующим номеру
шага, на котором найдено приближенное
минимальное значение точки минимума[2].
выбирается соответствующим номеру
шага, на котором найдено приближенное
минимальное значение точки минимума[2].
Заметим,
что метод (1) выгодно отличается простотой
реализации и не требует большой машинной
памяти. Недостатком метода (1), как и
метода ломаных, является необходимость
априорного знания константы
 из
условия Липшица.
из
условия Липшица.
Метод
последовательного перебора, аналогичный
методу (2),
можно предложить и для некоторых других
классов функций. Остановимся
на классе функций, дважды .дифференцируемых
на отрезке ,
у которых
,
у которых
 ,
где
,
где - некоторая фиксированная константа.
Обозначим этот класс функций через
- некоторая фиксированная константа.
Обозначим этот класс функций через .
Заметим, что если
.
Заметим, что если ,
то
,
то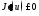 ,
и следовательно,
,
и следовательно,
 монотонно
убывает на
монотонно
убывает на
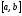 .
Это
значит, что тогда функция
.
Это
значит, что тогда функция
 достигает своей нижней грани при
достигает своей нижней грани при или
или
 .
Таким образом, задача минимизации
функций из класса
.
Таким образом, задача минимизации
функций из класса в
случае
в
случае
 решается
просто. Поэтому имеет смысл рассматривать
класс
решается
просто. Поэтому имеет смысл рассматривать
класс
 при
при
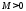 .
.
Тогда
для решения задачи минимизации первого
типа на классе функций
 можно
предложить следующий метод последовательного
перебора
можно
предложить следующий метод последовательного
перебора
 (2)
(2)
где,
 ,
, ,
а число
,
а число определяется
условием
определяется
условием
 [2].
[2].
Теорема2.2.
Применяя
метод
(2.2),
задачу минимизации первого типа для
любой функции
 можно
решить с заданной точностью
можно
решить с заданной точностью
 ,
т.
е.
,
т.
е.
 .
(2.4)
.
(2.4)
В
худшем случае (например, если
 )
может оказаться, что
)
может оказаться, что ,
,
 ,
и тогда
метод
(2.3) переходит в метод равномерного
перебора с шагом
,
и тогда
метод
(2.3) переходит в метод равномерного
перебора с шагом
 .
Если же
.
Если же при
некоторых
при
некоторых
 (например,
для
(например,
для
 ),
то методом (3) удается получить неравенство
(4), вообще говоря, при меньшем
),
то методом (3) удается получить неравенство
(4), вообще говоря, при меньшем ,
чем методом равномерного перебора.
Недостатком метода (3) является требование
знания константы
,
чем методом равномерного перебора.
Недостатком метода (3) является требование
знания константы .
.
