
- •Геометрический смысл модуля и аргумента производной
- •1. Сохранение угла между кривыми
- •2. Постоянство растяжений
- •3. Определение конформного отображения
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3. Функция Жуковского
- •4. Функция
- •5. Тригонометрические функции и
- •6. Гиперболические функции и
4. Функция
Рассмотрим основные свойства данной функции.
1. Однолистность.
Найдем условие, которому должна
удовлетворять область
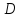 ,
чтобы отображение
,
чтобы отображение
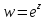 (3.1.1)
(3.1.1)
было однолистным в этой области.
Если
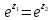 ,
т.е.
,
т.е.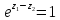 ,
то
,
то
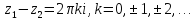 (3.1.2)
(3.1.2)
Следовательно, для однолистности
отображения (3.1.1) необходимо и достаточно,
чтобы область
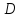 не содержала никакой пары различных
точек, удовлетворяющих условию (3.1.2).
не содержала никакой пары различных
точек, удовлетворяющих условию (3.1.2).
2. Периодичность.
По формуле Эйлера
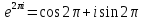 =1,
то для любого
=1,
то для любого имеем
имеем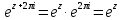 .
.
С другой стороны, пусть
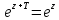 .
Умножая обе части на
.
Умножая обе части на получаем
получаем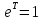 откуда, полагая
откуда, полагая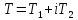 ,
имеем
,
имеем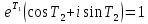 .
Но тогда
.
Но тогда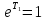 ,
то есть
,
то есть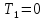 и
и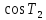 =1
и
=1
и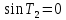 ,
то есть
,
то есть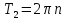 ,
где
,
где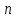 – целое число. Таким образом,
– целое число. Таким образом,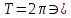 и
и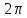 являются основными периодами.
являются основными периодами.
3. Конформность.
Так как производная функции (3.1.1) во всех
точках отлична от нуля, то отображение
конформно во всех точках конечной
плоскости
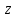 .
.
4. Образы точек конечной плоскости.
Рассмотрим отображения, осуществляемые
посредством этой функции. Заметим, что
функция никогда не принимает значение
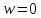 .
Это значит, что начало координат плоскости
.
Это значит, что начало координат плоскости не принадлежит к образу конечной
плоскости
не принадлежит к образу конечной
плоскости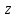 при отображении (3.1.1). Покажем, что всякая
другая конечная точка плоскости
при отображении (3.1.1). Покажем, что всякая
другая конечная точка плоскости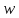 принадлежит к этому образу. В самом
деле, из уравнения
принадлежит к этому образу. В самом
деле, из уравнения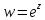 ,
где
,
где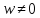 задано, а
задано, а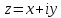 – неизвестное, получаем:
– неизвестное, получаем:
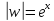 ,
откуда
,
откуда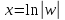 и
и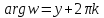 ,
то есть
,
то есть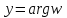 .
.
Итак, прообразами точек
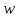 могут быть только точки вида
могут быть только точки вида
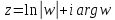 .
.
Очевидно, их бесконечно много, так как
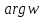 имеет бесконечное множество значений,
различающиеся попарно на целые кратные
имеет бесконечное множество значений,
различающиеся попарно на целые кратные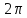 .
Кроме того, каждая из найденных точек
действительно есть прообраз точки
.
Кроме того, каждая из найденных точек
действительно есть прообраз точки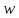 ,
так как
,
так как
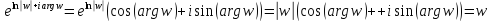 . (3.1.3)
. (3.1.3)
Итак, множество всех корней уравнения
 ,
где
,
где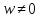 представляются формулой
представляются формулой
 =
=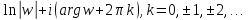
Все эти точки расположены на одной
прямой, параллельной мнимой оси на
расстоянии
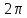 друг от друга.
друг от друга.
То есть функция (3.1.1) отображает конечную
плоскость
 на область, получающуюся из конечной
плоскости
на область, получающуюся из конечной
плоскости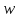 путем исключения одной точки
путем исключения одной точки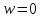 ,
при чем отображение не взаимно однозначно,
так как каждая точка
,
при чем отображение не взаимно однозначно,
так как каждая точка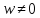 имеет бесконечное множество прообразов
(3.1.3).
имеет бесконечное множество прообразов
(3.1.3).
5. Образы прямых, параллельных осям координат.
Заставим
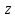 описывать какую-нибудь прямую, параллельную
одной из координатных осей (Рис. 3.1.1).
описывать какую-нибудь прямую, параллельную
одной из координатных осей (Рис. 3.1.1).
Рисунок 3.1.1.
Если это будет прямая
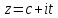 ,
параллельная мнимой оси, то
,
параллельная мнимой оси, то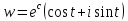 ,
то есть
,
то есть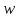 будет находиться на окружности с центром
в начале координат и радиусом, равным
будет находиться на окружности с центром
в начале координат и радиусом, равным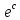 .
При этом, когда точка
.
При этом, когда точка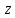 описывает прямую однократно так, что
ордината этой точки, равная
описывает прямую однократно так, что
ордината этой точки, равная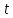 ,
непрерывно растет от -∞ до +∞, то
,
непрерывно растет от -∞ до +∞, то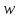 описывает соответствующую окружность
бесконечное множество раз в одном и том
же положительном направлении.
описывает соответствующую окружность
бесконечное множество раз в одном и том
же положительном направлении.
Если же точка
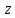 описывает прямую
описывает прямую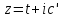 ,
параллельную действительной оси, то
,
параллельную действительной оси, то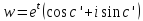 ,
очевидно, пробегает прямолинейный луч,
выходящий из начала координат и образующий
с положительной частью действительной
оси угол
,
очевидно, пробегает прямолинейный луч,
выходящий из начала координат и образующий
с положительной частью действительной
оси угол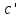 .
При этом, когда точка
.
При этом, когда точка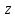 описывает однократно так, что абсцисса
этой точки, равная
описывает однократно так, что абсцисса
этой точки, равная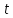 ,
непрерывно растет от -∞ до +∞, то
,
непрерывно растет от -∞ до +∞, то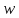 описывает соответствующий луч однократно
так, что расстояние этой точки от начала
координат непрерывно растет от 0до ∞
(и тот и другой пределы исключаются, так
как
описывает соответствующий луч однократно
так, что расстояние этой точки от начала
координат непрерывно растет от 0до ∞
(и тот и другой пределы исключаются, так
как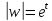 ).
).
Итак, при отображении плоскости
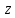 посредством функции
посредством функции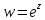 семейство прямых, параллельных мнимой
оси преобразуется в семейство окружностей
с центром в начале координат, а семейство
прямых, параллельных действительной
оси, – в семейство прямолинейных лучей,
выходящих из начала координат.
семейство прямых, параллельных мнимой
оси преобразуется в семейство окружностей
с центром в начале координат, а семейство
прямых, параллельных действительной
оси, – в семейство прямолинейных лучей,
выходящих из начала координат.
6. Образы полос, параллельных действительной оси.
Рассмотрим область
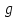 ,
представляющую внутренность прямоугольной
полосы шириной
,
представляющую внутренность прямоугольной
полосы шириной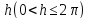 ,
параллельной действительной оси. Пусть
эта полоса ограничена линиями
,
параллельной действительной оси. Пусть
эта полоса ограничена линиями и
и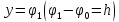 .
Из установленного выше следует, что
образ области
.
Из установленного выше следует, что
образ области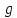 в плоскости
в плоскости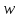 будет область
будет область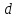 ,
представляющая угол раствора
,
представляющая угол раствора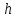 с вершиной в начале координат, ограниченный
прямолинейными лучами
с вершиной в начале координат, ограниченный
прямолинейными лучами и
и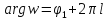 (Рис. 3.1.2).
(Рис. 3.1.2).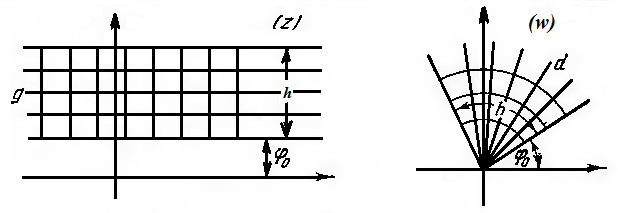
Рисунок 3.1.2.
При этом соответствие между точками
областей
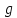 и
и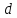 ,
устанавливаемое посредством функции
(3.4.1.), будет взаимно однозначным, поскольку
прообразами некоторой точки
,
устанавливаемое посредством функции
(3.4.1.), будет взаимно однозначным, поскольку
прообразами некоторой точки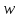 из области
из области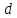 могут быть только точки
могут быть только точки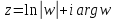 ,
различающиеся друг от друга значениями
мнимой части. Две такие точки лежат на
одной прямой, параллельной мнимой оси,
на расстоянии, кратном
,
различающиеся друг от друга значениями
мнимой части. Две такие точки лежат на
одной прямой, параллельной мнимой оси,
на расстоянии, кратном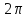 .
Но полоса
.
Но полоса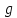 имеет ширину не более
имеет ширину не более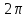 ,
поэтому она может содержать внутри лишь
один прообраз точки
,
поэтому она может содержать внутри лишь
один прообраз точки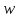 .
Итак, каждая точка
.
Итак, каждая точка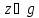 имеет лишь один образ и каждая точка
имеет лишь один образ и каждая точка лишь один прообраз внутри
лишь один прообраз внутри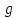 ,
что выражает взаимную однозначность
отображения.
,
что выражает взаимную однозначность
отображения.
При этом показательная функция взаимно
однозначно и конформно отображает
полосу ширины
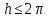 ,
параллельную действительной оси, на
угол раствора
,
параллельную действительной оси, на
угол раствора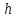 с вершиной в начале координат. Поэтому
к показательной функции прибегают
каждый раз, когда надо отобразить
некоторую прямолинейную полосу на
внутренность угла.
с вершиной в начале координат. Поэтому
к показательной функции прибегают
каждый раз, когда надо отобразить
некоторую прямолинейную полосу на
внутренность угла.
7. Образ прямой, не параллельной ни одной из оси координат.
Если прямая плоскости
 не является параллельной какой-либо
оси координат, то образ её в плоскости
не является параллельной какой-либо
оси координат, то образ её в плоскости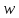 будет уже не прямой и не окружностью, а
логарифмической спиралью. В самом деле,
если эта прямая есть
будет уже не прямой и не окружностью, а
логарифмической спиралью. В самом деле,
если эта прямая есть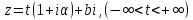 (
(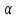 – угловой коэффициент прямой, а
– угловой коэффициент прямой, а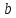 – ордината в начале), то образом будет
кривая
– ордината в начале), то образом будет
кривая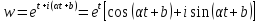 .
Здесь
.
Здесь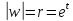 ,
,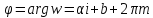 ,
или, исключая параметр
,
или, исключая параметр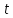 :
: .
Но
.
Но или полярный угол
или полярный угол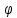 определен только с точностью до целого
кратного от
определен только с точностью до целого
кратного от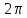 .
Поэтому, обозначая
.
Поэтому, обозначая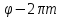 снова через
снова через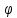 получаем:
получаем: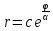 ,
где
,
где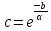 .
.
Это и есть уравнение логарифмической
спирали (Рис. 3.1.3). Из того, что она является
образом прямой есть
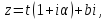 пересекающей прямые, параллельные
действительной оси под постоянным углом
пересекающей прямые, параллельные
действительной оси под постоянным углом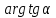 ,
следует в силу конформности отображения,
что и логарифмическая спираль пересекается
под тем же углом образы указанных прямых,
то есть все лучи, выходящие из начала
координат. Мы получили характеристическое
свойство логарифмической спирали.
,
следует в силу конформности отображения,
что и логарифмическая спираль пересекается
под тем же углом образы указанных прямых,
то есть все лучи, выходящие из начала
координат. Мы получили характеристическое
свойство логарифмической спирали.

Рисунок 3.1.3.
Пример 3.1.1. Из приведенных свойств
(1) и (2) вытекает, что функция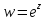 конформно
отображает прямоугольник
конформно
отображает прямоугольник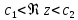 ,
, ,
где
,
где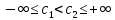 ,
,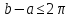 на кольцевой сектор
на кольцевой сектор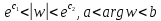 .
Частные случаи таких отображений
показаны на рис. 3.1.4.
.
Частные случаи таких отображений
показаны на рис. 3.1.4.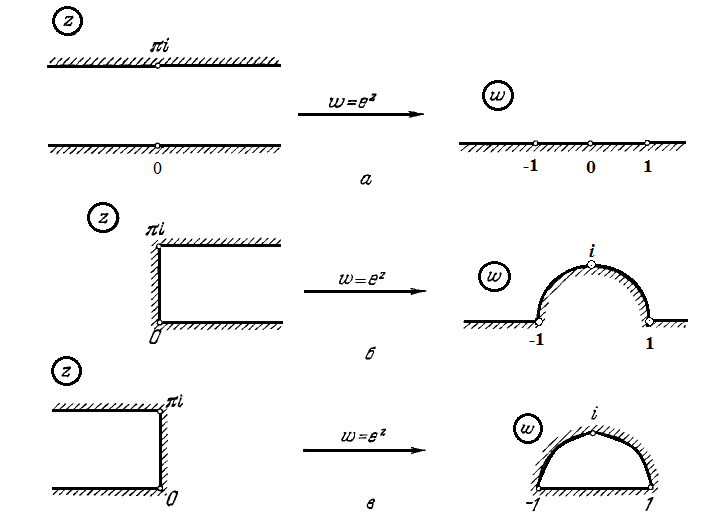
Рисунок 3.1.4.
Пример 3.1.2. Найдем образ отрезка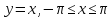 при отображении
при отображении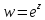 .
.
Рисунок 3.1.5.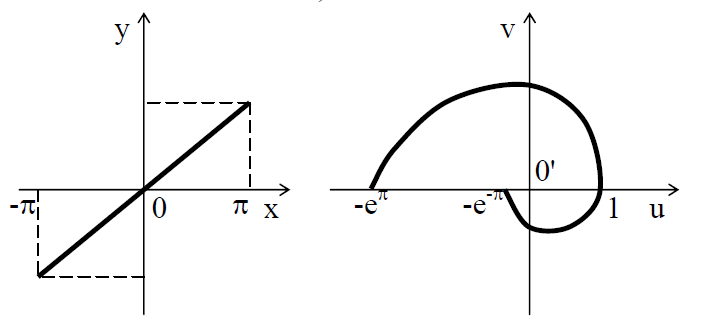
Любая точка отрезка имеет комплексную
координату
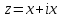 ,
,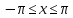 .
Поэтому её образом служит линия,
параметрически заданная уравнениями
.
Поэтому её образом служит линия,
параметрически заданная уравнениями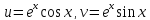 .
Это дуга логарифмической спирали
(рис. 3.4.5).
.
Это дуга логарифмической спирали
(рис. 3.4.5).
