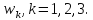- •Геометрический смысл модуля и аргумента производной
- •1. Сохранение угла между кривыми
- •2. Постоянство растяжений
- •3. Определение конформного отображения
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3. Функция Жуковского
- •4. Функция
- •5. Тригонометрические функции и
- •6. Гиперболические функции и
1. Линейная функция
Определение.Линейной функциейназывается функция вида:
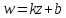 , (1.1.)
, (1.1.)
где
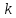 и
и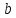 – некоторые постоянные комплексные
числа
– некоторые постоянные комплексные
числа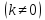 .
.
Очевидно, что отображение (1.1.) будет
конформным во всей плоскости комплексного
переменного
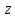 и при том взаимно однозначным.
и при том взаимно однозначным.
Рассмотрим сначала три случая, при чем,
для простоты
 и
и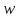 будем изображать точками одной плоскости.
будем изображать точками одной плоскости.
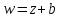 .
.
Это отображение есть сложение векторов,
а, фактически, параллельный перенос
точек плоскости на вектор
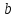 .(Рис.
2.1.1).
.(Рис.
2.1.1).
Рисунок 2.1.1.
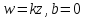 .
.
Пусть
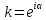 ,
тогда
,
тогда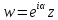 .
В этом случае имеем:
.
В этом случае имеем:
 ,
,
то есть точка
 переходит в точку
переходит в точку при помощи вокруг поворота около нулевой
точки на угол
при помощи вокруг поворота около нулевой
точки на угол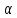 .
Значит, это отображение есть поворот
вокруг начала координат на угол
.
Значит, это отображение есть поворот
вокруг начала координат на угол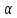 (Рис. 2.1.2).
(Рис. 2.1.2).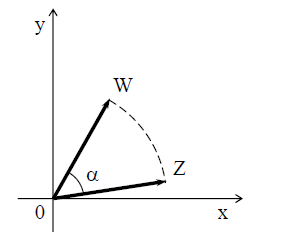
Рисунок 2.1.2.
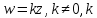 – постоянное комплексное число (если
– постоянное комплексное число (если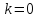 ,
то все точки комплексной плоскости
перейдут в нулевую точку).
,
то все точки комплексной плоскости
перейдут в нулевую точку).
Запишем
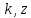 в показательной форме, тогда получим
в показательной форме, тогда получим
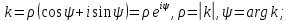
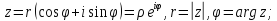
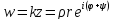 .
.
Это означает, что длина вектора
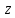 меняется в
меняется в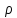 раз (то есть
раз (то есть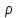 – коэффициент подобия) и к аргументу
– коэффициент подобия) и к аргументу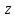 прибавляется угол
прибавляется угол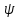 (поворот вокруг начала координат на
угол
(поворот вокруг начала координат на
угол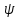 ).
).
Окончательно получим, что отображение,
осуществляемое функцией
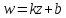 ,
есть комбинация преобразований точек
плоскости:
,
есть комбинация преобразований точек
плоскости:
поворот вокруг начала координат на угол, равный аргументу числа
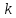 ;
;подобие с центром в начале координат и коэффициентом подобия
 равным модулю числа
равным модулю числа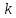 ;
;параллельный перенос на вектор
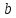 ,
при котором начало координат переходит
в точку
,
при котором начало координат переходит
в точку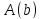 .
.
Функция
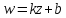 является аналитической.
является аналитической.
При отображении, осуществляемом с
помощью линейной функции, фигуры
переходят в подобные им фигуры (на рис.
2.1.3. это показано для функции
 ).
Это свойство называетсясвойством
сохранения формы.
).
Это свойство называетсясвойством
сохранения формы.
Рисунок 2.1.3.
Этим свойством обладает и преобразование
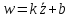 ,
которое называетсяантилинейным.
Оно сохраняет форму, но меняет ориентацию
обхода границы фигуры на противоположную
(На Рис. 2.1.4. это показано для функции
,
которое называетсяантилинейным.
Оно сохраняет форму, но меняет ориентацию
обхода границы фигуры на противоположную
(На Рис. 2.1.4. это показано для функции )
)
Рисунок 2.1.4.
Отсюда вытекает, что любое преобразование подобия задается линейной или антилинейной функцией, при чем если ориентация сохраняется, то оно задается линейной функцией.
Поскольку линейная функция
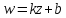 определяется двумя параметрами
определяется двумя параметрами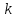 и
и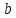 ,
то для её задания нужны два условия.
,
то для её задания нужны два условия.
2. Дробно-линейная функция
Линейная функция является частным случаем функции вида:
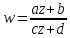 (2.2.1)
(2.2.1)
где
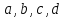 – комплексные число, при чем
– комплексные число, при чем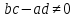 .
.
Функции вида (2.2.1) называются дробно-рациональными.
Дробно-линейную функцию можно распространять на всю расширенную комплексную плоскость.
Так как
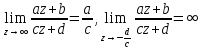 ,
то точка
,
то точка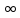 переходит при этом отображении в
переходит при этом отображении в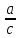 ,
а точка
,
а точка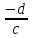 в
в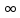 .
.
Рассмотрим основные свойство дробно-линейных отображений.
1. Конформность.
Дробно линейная функция конформно отображает расширенную комплексную плоскость на расширенную комплексную плоскость.
Очевидно, что функция (2.2.1) регулярна во
всей расширенной комплексной плоскость,
за исключением точки
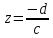 – полюса первого порядка. Решая уравнение
(2.2.1) относительно
– полюса первого порядка. Решая уравнение
(2.2.1) относительно ,
находим функцию
,
находим функцию
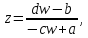 (2.2.2)
(2.2.2)
( )
обратную к функции (2.2.1).
)
обратную к функции (2.2.1).
Функция (2.2.2) однозначна на всей расширенной комплексной плоскости и так же дробно-линейной. Следовательно, дробно-линейная функция однолистна в расширенной комплексной плоскости.
2. Групповое свойство.
Совокупность дробно-линейных отображений образует группу, т.е.
1)суперпозиция дробно-линейных отображений является дробно-линейным отображением.
2) Отображение, обратное к дробно-линейному, так же является дробно-линейным.
Докажем первое свойство. Пусть
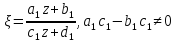 (2.2.3)
(2.2.3)
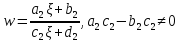 (2.2.4)
(2.2.4)
Подставляя (2.2.3) в (2.2.4) получаем:
 где
где
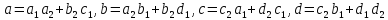 .
.
Второе свойство доказано в предыдущем пункте.
2. Круговое свойство.
При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая.
Докажем это свойство. Сначала рассмотрим
линейное отображение
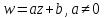 .
Это отображение сводится к подобию,
повороту и переносу (пункт 1). Следовательно,
линейное отображение переводит окружности
в окружности, а прямые – в прямые.
.
Это отображение сводится к подобию,
повороту и переносу (пункт 1). Следовательно,
линейное отображение переводит окружности
в окружности, а прямые – в прямые.
В случае, когда дробно-линейная функция
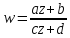 не является линейной
не является линейной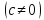 ,
представим её в виде
,
представим её в виде
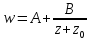 , (2.2.5)
, (2.2.5)
где
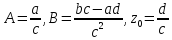 .
Тогда отображение (2.2.5) сводится к
последовательному выполнению следующих
отображений:
.
Тогда отображение (2.2.5) сводится к
последовательному выполнению следующих
отображений:
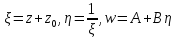 (2.2.6)
(2.2.6)
Первое и третье отображения (2.2.6) обладают круговым свойством, так как они линейные. Остается доказать, что второе отображение (2.2.6), т.е. отображение
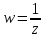 ,
(2.2.7)
,
(2.2.7)
так же обладает круговым свойством.
Уравнение любой окружности или прямой
на плоскости
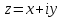 имеет вид
имеет вид
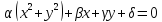 (2.2.8)
(2.2.8)
(если
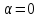 ,
то (3.2.9) – уравнение прямой).
,
то (3.2.9) – уравнение прямой).
Так как
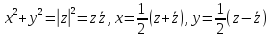 ,
то уравнение (2.2.8) записывается в виде
,
то уравнение (2.2.8) записывается в виде
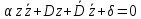 ,
(2.2.9)
,
(2.2.9)
где
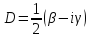 .
.
Подставив в (2.2.9)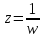 получаем
получаем
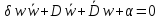 .
(2.2.10)
.
(2.2.10)
Следовательно, образом окружности
(2.2.9) (прямой, если
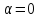 )
при отображении (2.2.7) является окружность
(2.2.10) (прямая, если
)
при отображении (2.2.7) является окружность
(2.2.10) (прямая, если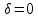 ).
).
Отметим, что дробно-линейное отображение
 переводит окружности и прямые, проходящие
через точку
переводит окружности и прямые, проходящие
через точку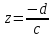 в прямые, а остальные окружности и прямые
– в окружности.
в прямые, а остальные окружности и прямые
– в окружности.
Принято считать, что прямая – это окружность бесконечного радиуса. Поэтому коротко круговое свойство можно сформулировать так: при дробно-линейном отображении окружности переходят в окружности.
4. Свойство сохранения симметрии.
Понятие симметрии относительно окружности
определяется в элементарной геометрии
следующим образом. Пусть
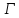 – окружность радиуса
– окружность радиуса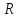 с центром в точке
с центром в точке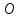 .
.
Определение. Точки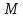 и
и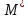 называются симметричными относительно
окружности
называются симметричными относительно
окружности ,
если они лежат на одном луче, выходящем
из точки
,
если они лежат на одном луче, выходящем
из точки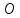 ,
и
,
и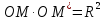 (Рис. 3.2.1).
(Рис. 3.2.1).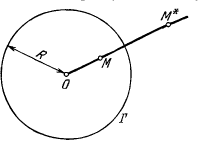
Рисунок 2.2.1.
В частности, каждая точка окружности
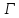 является симметричной сама себе
относительно этой окружности.
является симметричной сама себе
относительно этой окружности.
Таким образом, на комплексной плоскости
точки
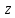 и
и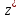 являются симметричными относительно
окружности
являются симметричными относительно
окружности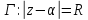 ,
если они лежат на одном луче, выходящем
из точки
,
если они лежат на одном луче, выходящем
из точки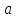 и
и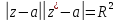 .
Из этого определения вытекает, что
симметричными относительно окружности
.
Из этого определения вытекает, что
симметричными относительно окружности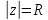 точки
точки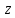 ,
, связаны соотношением
связаны соотношением
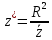 (2.2.11)
(2.2.11)
В частности, симметричные относительно
единичной окружности
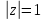 точки
точки и
и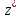 связаны соотношением:
связаны соотношением:
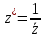 (2.2.12)
(2.2.12)
Так как точки
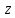 и
и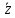 симметрично относительно действительной
оси, то из (2.2.12) следует, что точка
симметрично относительно действительной
оси, то из (2.2.12) следует, что точка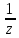 получается из точки
получается из точки двойной симметрией: относительно
действительной оси и относительно
единичной окружность (в любом порядке).
двойной симметрией: относительно
действительной оси и относительно
единичной окружность (в любом порядке).
Из (2.2.11) вытекает, что симметричные
относительно окружности
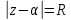 точки
точки и
и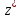 связаны соотношением
связаны соотношением
 (2.2.13).
(2.2.13).
Стоит отметить, что точки
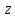 и
и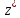 являются симметричными относительно
окружности
являются симметричными относительно
окружности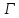 тогда и только тогда, когда любая
окружность
тогда и только тогда, когда любая
окружность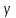 ,
проходящая через эти точки, пересекается
с окружностью
,
проходящая через эти точки, пересекается
с окружностью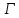 под прямым углом.
под прямым углом.
Дробно-линейное отображение обладает следующим свойством сохранения симметрии.
При дробно-линейном отображении пара точек, симметричных относительно окружности, переходит в пару точек, симметричных относительно образа этой окружности.
Здесь окружность, в частности, может быть прямой.
Докажем это свойство. Пусть точки
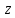 и
и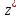 симметричны относительно окружности
симметричны относительно окружности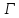 и пусть дробно-линейное отображение
и пусть дробно-линейное отображение переводит
окружность
переводит
окружность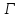 в
в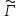 ,
а точки
,
а точки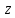 и
и – в точки
– в точки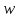 и
и соответственно. В силу кругового свойства
соответственно. В силу кругового свойства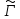 является окружностью. Нужно доказать,
что точки
является окружностью. Нужно доказать,
что точки и
и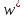 симметричны относительно
симметричны относительно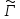 .
Для этого достаточно доказать, что любая
окружность
.
Для этого достаточно доказать, что любая
окружность ,
проходящая через точки
,
проходящая через точки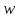 и
и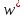 ,
пересекается с
,
пересекается с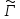 под прямым углом.
под прямым углом.
Прообразом окружности
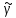 при дробно-линейном отображении
при дробно-линейном отображении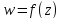 является окружность
является окружность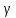 ,
проходящая через точки
,
проходящая через точки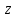 и
и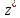 .
Эта окружность
.
Эта окружность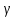 пересекается с
пересекается с под прямым углом. Следовательно,
под прямым углом. Следовательно,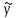 пересекается с
пересекается с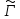 так же под прямым углом, так как
дробно-линейное отображение является
конформным во всей расширенной плоскости
и сохраняет углы между кривыми в каждой
точке.
так же под прямым углом, так как
дробно-линейное отображение является
конформным во всей расширенной плоскости
и сохраняет углы между кривыми в каждой
точке.
5. Дробно-линейное отображение, переводящее три точки в три точки.
Существует единственное дробно-линейное
отображение, при котором три различные
точки
 переходят в три различные точки
переходят в три различные точки .
Это отображение определяется формулой
.
Это отображение определяется формулой
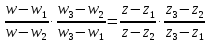 (2.2.14)
(2.2.14)
Докажем это свойство. Из группового
свойства следует, что функция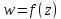 ,
определяемая соотношением (2.2.14), является
дробно-линейной. Так же ясно, что
,
определяемая соотношением (2.2.14), является
дробно-линейной. Так же ясно, что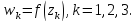
Докажем, что если дробно-линейная функция
 удовлетворяет тем же условиям, что и
удовлетворяет тем же условиям, что и ,а
именно
,а
именно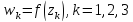 ,
то
,
то .
Пусть
.
Пусть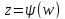 – функция, обратная функции
– функция, обратная функции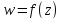 .
Тогда
.
Тогда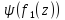 – дробно-линейная функция:
– дробно-линейная функция:
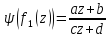 и
и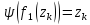 .
То есть
.
То есть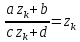 ,
,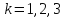
Отсюда получаем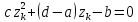 ,то
есть квадратное уравнение
,то
есть квадратное уравнение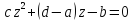 имеет три различных корня. Следовательно,
имеет три различных корня. Следовательно,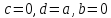 и
и ,
откуда
,
откуда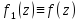 .Свойство
доказано.
.Свойство
доказано.
Заметим, что функция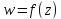 ,определенная
формулой (3.2.15), конформно отображает
круг, граница которого проходит через
точки
,определенная
формулой (3.2.15), конформно отображает
круг, граница которого проходит через
точки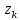 ,
,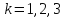 ,
на круг, граница которого проходит через
точки
,
на круг, граница которого проходит через
точки