матлогика - шпора

1.Определение алгоритма и способы их записей.

2.Принятые обозначения при описании алгоритмов.

3.Пошаговое описание алгоритмов.

4.Описание алгоритмов в виде блок-схем.

5.Свойства алгоритмов.

6.Критерии эффективности и сложность алгоритмов.

7.Классификация задач по степени сложности.

8.Сущность метода математической индукции (МИ).

9.Построение доказательства по методу МИ.

10.Примеры доказательств с использованием метода МИ.

11.Использование метода МИ для исследования алгоритмов.

12.Недетерминированные и детерминированные алгоритмы.

13.Разделы математической логики, представление операций булевой логики через множества и их отображение с помощью диаграмм Эйлера-Венна.

14.Объединение множеств и переход от предметной переем. х к логич.перем. Х1

и Х2 .

15.Пересечение множеств, … и обл. взаимод. двух мн. на диаг. Эйлера-Венна.

16.Таблицы истинности для дизъюнкции и конъюнкции.

17.Операции стрелка Пирса и штрих Шеффера.

18.Операции разности и импликации.

19.Операции симметрической разности и эквивалентности.

20.Формы представления булевых функций (СДНФ, СКНФ, СПНФ).

21.Двойственность в булевой логике.

22.Различия отображения логических функций в СДНФ. СКНФ и СПНФ.

23.Минимальные нормальные формы логических функций.

24.Принцип суперпозиции в булевой логике и приоритеты логических операций.

25.Классы элементарных логических функций.

26.Законы логики Буля.

27.Применение закона поглощения для нескольких переменных.

28.Аксиоматический подход к доказательству логических выражений в булевой

29.Доказательство логических выражений с помощью диаграмм Эйлера-Венна.

30.Доказательство логических выражений с использованием таблиц истинности.

31.Способы доказ.логических выражений с использованием спец. приемов.

32.Логика высказываний и операции логики высказываний.

33.Таблицы истинности операций логики высказываний.

34.Различия логики Буля и логики высказываний.

35.Метаязык логики высказываний ….

36.Аксиомы, противоречия и тавтологии в логике высказываний.

37.Конструктивный подход к доказательству логических выражений в логике высказываний.

38.Минимальная нормальная форма, мин. и трансв. покр. в логике высказываний.

39.Доказательство логических высказываний с помощью метода резолюций.

40.Логика предикатов.

41.Минимизация логических выражений методом Куайна (Квайна).

42.Минимизация логических выражений в логике Буля путем склеивания в СДНФ и СКНФ. Показать, в чем различие склеивания в этих двух формах.

43.Асимптотические представления и анализ алгоритмов.

1. Определение алгоритма и способы их записей.

Алгоритм - точное и понятное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи.

Название «алгоритм» произошло от латинской формы имени среднеазиатского математика Аль - Хорезми - Algorithmi. В средние века алгоритм трансформировался в алгоритм и стал обозначать 4 арифметические действия «+», «-», умножить, разделить. Алгоритмизация задач является одним из самых важных этапов ее решения на ЭВМ.

С возникновением науки кибернетики в 40-х годах 20в. под алгоритмом стали понимать точное описание последовательности деятельности исполнителя любого компьютера направленных на решение поставленной задачи.

Алгоритм - одно из основных понятий информатики и математики. Исполнитель алгоритма - это некоторая абстрактная или реальная

(техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.

Форма записи алгоритма:

На практике наиболее распространены следующие формы представления алгоритмов:

1.Словесный. Словами могут быть представлены достаточно просто только самые простые алгоритмы (Примеры приготовления лекарств, блюд, пдд и др.)

2.Пошаговый. С его помощью в результате выделения последовательности действий можно описать алгоритмы арабских инфор. структур, алгоритмы решения задания, упражнений контроля, задач проектирования и моделирования, вычислительных и оптимизационных задач.

3.Математический. В виде последовательности формул, которые необходимо вычислить в процессе решения задачи. Последовательности формул иногда объединяются в блоки так же иногда используются пошаговые описания последовательности выполнения блоков, которая в общем случае может быть не просто линейной, но и иметь также разветвления в зависимости от проверок некоторых условий, а так же может иметь циклы.

4.Описания алгоритма в виде блок схем. Применяется для повышенной наглядности и лучшей обозримости алгоритмов записанных пошаговым или математическим способом. Этот способ помогает легче составить и отладить программу с помощью которой алгоритм будет реализован на ЭВМ.

2.Принятые обозначения при описании алгоритмов.

- операция замещения (подстановка, присваивание); m n – значит m замещено текущим значением n ;

n n+1 – увеличение n на 1(n заменить на n+1);

n m r – значениям n и m присвоить r;

n m – обмен значениями переменных, фактически выполняются через некоторую промежуточную переменную (t n, n m, m t)

n = m? – операция сравнения (вместо равенства может быть любой другой знак операции отношения , >, <, , )

V[j] – j - элемент из множества V1 , V 2 , V 3 ,…, V i ,…, V n (от одномерного массива)

a [i,j] – Элемент на пересечении i-ой строки и j-ой столбца матрицы А (двумерного массива)

3. Пошаговое описание алгоритмов.

Каждый шаг алгоритма записывается в виде некоторого идентификатора, первая позиция которого может быть произвольной. Буква латинского: E, K, L, M, N и т.д. или буквы русского алфавита, чаще всего: Ш(шаг). 2-ой и следующие позиции отражают номера шагов в алгоритме. Ш1 , Ш 2 , Ш 3 … Е1 , Е 2 , Е 3 …

Иногда применяют цифровое обозначение: 1, 2, … и т.д. Описание каждого шага начинается с резюмирующей фразы, которая кротко обозначает суть каждого шага. Резюмирующую фразу (Р.Ф.) заключают в квадратные скобки [Резюмирующую фразу].

После Р.Ф. следует описание словами тех действий, которые должны быть выполнены на данном шаге или тех решений, которые должны быть выполнены. Здесь допустимы комментарии, которые заключают в (…). Комментарии позволяют понять цель и суть данного шага, указывают на некоторую особенность перемещений, изменяющихся на данном шаге и т.д.

Рассмотрим пример:

Задача:

Даны 2 целых положительных m и n. Найти их НОД. Рассмотрим алгоритм Евклида записанный в виде шагов:

Ш1. {Нахождение остатка} Разделим m на n и пусть остаток = r. (у нас получится 0 ≤ r ≤ n)

Ш2.{Остаток 0?} Если r = 0,то алгоритм закончен и n - искомое число. Ш3.{Замещение} Положим m←n; n←r и вернемся к Ш1.

Для того, чтобы проверить можно ли использовать алгоритм в работе необходимо испытать его в ручную или с помощью программы на ЭВМ. Это наиболее простой и рациональный способ, чтобы понять алгоритм.

4. Описание алгоритмов в виде блок-схем.

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется схемой алгоритма или блоксхемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.

Расчет

Вычисления по

параметров подпрограмме, стандартной программе

Начало, конец алгоритма, начало вход и выход в

подпрограмму

Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

5. Свойства алгоритмов.

Кроме того, что алгоритм это свод конечного числа правил, задающих последовательность выполнения действий при решении задачи, он должен обладать следующими свойствами:

1)Конечность (финитность) – любой алгоритм должен заканчиваться за конечное число шагов. Например, алгоритм поиска НОД удовлетворяет этому условию. Ш1 значение остатка r ≤ n, и если r≠0, то к следующему выполнению Ш1 значение n уменьшается т.о. получается убывающая последовательность целых ―+‖ n, который заканчивается, когда r=0, т.е. за конечное число раз.

2)Определенность – каждый шаг алгоритма должен быть точно определен. Действия, которые необходимо выполнить, должны быть строго и недвусмысленно заданы в каждом возможном случае.

3)Ввод исходных данных – любой алгоритм имеет некоторое число входных данных, которые задаются ему до начала работы. Эти данные берутся из конкретного допустимого множества. Например, для алгоритма поиска НОД входных величины m и n выбираются из множества натуральных чисел.

4)Вывод результата (результатов) – любой алгоритм всегда имеет 1 и

несколько выходных величин, которые имеют определенное отношение к исходным данным, и получаются в результате их анализа и обработки в ходе выполнения алгоритма.

5)Эффективность – в общем случае это обозначает, все операции, которые выполняются в алгоритме, должны быть достаточно простыми и выполнятся за допустимое конечное время. Если существует несколько алгоритмов решения этой задачи, необходимо выбрать более эффективный алгоритм. Это означает, что для заданного алгоритма нужно найти его рабочие характеристики:

а) Это время выполнения работы алгоритма, в зависимости от объема входных данных;

б) объем памяти необходимый для проведения вычислений.

6)Правильность алгоритма - это способность алгоритма дать правильные результаты решения поставленной задачи. Практически правильность алгоритма подтверждается в результате проведения большого кол-ва испытания в которых проверяются все возможные случаи и состояния, учитываемые в реализации данного алгоритма.

Теоретически доказать правильность работы любого алгоритма можно с помощью метода МАТИНДУКЦИИ.

6. Критерии эффективности и сложность алгоритмов.

Эффективность алгоритма. В общем случае это означает что все операции, которые выполняются в алгоритме, должны быть достаточно простыми и выполнимыми за допустимое конечное время, если существует несколько алгоритмов решение одной задачи, то необходимо выбрать более эффективный алгоритм, для заданного алгоритма. Нужно найти его рабочие характеристики:

а) время выполнения алгоритма (количество шагов)

б) объем памяти необходим для выполнения вычислений.

Оценки времени выполнения алгоритмов в общем случае вычисляются достаточно сложно.

Пусть для алгоритма нахождения НОД поставлена задача:

n – известно, а m – любое целое положительное число, такое что m≤n. Определить: сколько в среднем раз (Тn) выполняется шаг Ш1 при достаточно

большом n.

Очевидно, чтобы найти среднее Тn необходимо испытать алгоритм для m=1, m=2, m=3, …, m=n и подсчитать при этом суммарное число выполнений Ш1 и разделить на n

который без испытаний и проведений определенных вычислений угадать невозможно.

Объем памяти, необходимый для проведения вычислений может увеличивать или уменьшать время выполнения алгоритма. Увеличение происходит при нехватке памяти => не имеем мощного компьютера - выбираем сложный алгоритм.

Формально любой алгоритм опр. Как некоторый вычислительный метод, представляющий собой некую четверку (Q,I,W,f)

Q- все возможные допустимые состояния вычислений при работе алгоритма. I - все множество допустимых входящих данных алгоритма

W - все множество выходных результатов.

F - правило вычислений в алгоритме, которое может быть очень сложным и состоять из многих действий.

Сложность алгоритма определяется:

1-время выполнения алгоритма

2-Необходимый объем памяти для вычисления

3-общее количеством шагов в алгоритме 4-вместо общего числа шагов можно подсчитывать кол-во шагов определенного

вида(например число арифметических операций при вычислении выражения)

7. Классификация задач по степени сложности.

Сложность задачи определяется через сложность наилучшего алгоритма, известного для ее решения.

Быстрыми алгоритмами являются линейные, которые обладают сложностью порядка n, и называются алгоритмами порядка 0(n), где n – размерность входного данного.

К линейным алгоритмам относятся:

алгоритм нахождения суммы для типичных чисел, состоящих из n1 и n2 цифр. Его сложность 0(n1)+n2.

Есть более быстрые алгоритмы, чем линейные. Например, алгоритм двоичного поиска в линейном упорядоченном массиве, его сложность 0(log2n), где n – длинна упорядоченного массива.

Другие хорошо известные алгоритмы: деление, извлечение квадр. корня – решение систем линейных уравнений попадают в более общий класс

полиномиальных алгоритмов.

Полиномиальные алгоритмы – алгоритмы, принадлежащие классу Р, эти алгоритмы имеют полиномиальную временную сложность и в общем виде их сложность записывается 0(nк), где к из Z, k>0.

Алгоритмы для которых не существует такой временной оценки – экспоненциальные. Задача, считается трудно решаемой. Если для нее не существует решающего эту задачу полиномиального алгоритма.

Отметим, что экспоненциальным алгоритмом при небольших значениях n может быть более быстрым, чем полиномиальным, однако различие между двумя этими типами задач очень велико и всегда проявляется при больших значениях n.

Класс Р: Задачу называем «хорошей» если для нее существует полиномиальный алгоритм (Рассоривать множество из n чисел(сложность 0(n2)), нахождение вершин, связанных цепочкой дуг(0(n+m)) и т.п.)

Класс Е:

Задачи, в которых требуется построить множество всех подмножеств данного множества, все полные подграфы полного графа.

Ни Р ни Е:

В условиях не содержится экспоненциальных вычислений, но для которых до сих пор не разработан точный и эффективный алгоритм, имеющий полиноминальную оценку (Решение систем уравнений с целочисленными переменными, оптимальный раскрой и т.п.)

8. Сущность метода математической индукции (МИ).

Впервые был применен для строгих доказательств в 1575 году итальянским ученым Франческа Мауролико. В начале XVII столетия Пьер де Ферма усовершенствовал этот метод и назвал его методом бесконечного спуска. Понятие «математическая индукция» была введена де Морганом в начале XIX века.

Математическая индукция как метод проверки правильности программирования для компьютеров был применен американским ученым Робертом Флайдом в 1967г. Фактически же идея индуктивных утверждений в начальном виде появилась еще в 1946г., когда Х.Гольстайн и Джон фон Нейман определили понятие блок-схемы программы.

Рассмотрим ММИ на примере анализа утверждения о целом числе n. Пусть P(n)-некоторое утверждение о числе n.

P1(n)=‖n(n+3)-четное число‖

P2(n)=‖если n≥10, то 2n≥n3‖

Предположим что мы хотим доказать что P(n)справедливо для всех положительных чисел n.

Суть доказательства по ММИ состоит в следующем:

Доказать что P(1)-справедливо

Дать доказательство того, что если P(1),P(2),…P(n)-справедливо, то справедливо P(n+1).

В качестве примера приведем соотношение известное с древних времен

1=12, 1+3=22, 1+3+5=32, 1+3+5+7=42, 1+3+5+7+9=52, …(*)

В общем виде это отношение можно записать 1+3+…(2n-1)=n2 (**)

Докажем это равенство с помощью ММИ, т.е. докажем что P(n) справедливо для всех положительных n. В соответствии с ММИ имеем:

P(1)=1-верно 1=12

Если все утверждения P(1),P(2),…,P(n)-верны то выполняется

соотношение(**). Добавим к обоим частям равенства (**) следующие слагаемые, которые необходимо проверить, получим 1+3+…+2n-1+2n+1=n2+2n+1=(n+1)2

Что показывает что P(n+1) также верно.

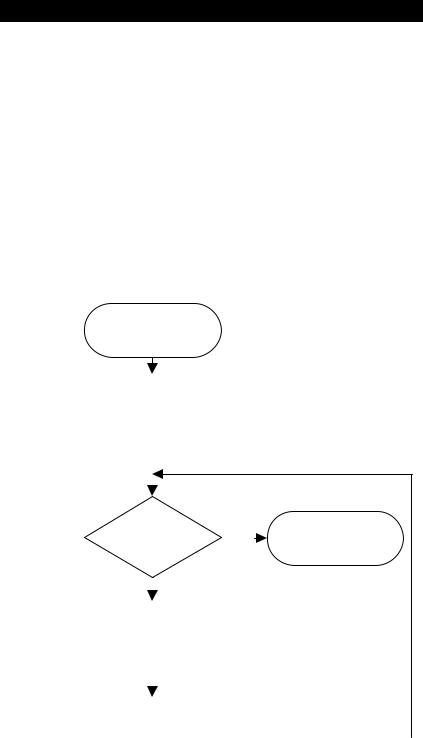
9. Построение доказательства по методу МИ.

I1: [Доказать Р(1)] Положить k=1 и согласно п а) выдать доказательство утверждения Р(1).

I2: [k=n?] Если k=n то алгоритм заканчивает работу и требуемое доказательство выдано, если k≠n то:

I3: [доказать Р(k+1)] Согласно пункту б) выдать доказательство того, что если P(1), P(2), …P(k) верны, то что P(k+1) также верно и сделать соответствующий вывод.

I4: [увеличить k] k k+1 и перейти на шаг I2

Формула оценки времени выполнения алгоритма Евклида:

Tn=(12*Ln(2)/п2)*Ln(n)

Блок схема алгоритма I(k=n)

(доказательство по методу математической индукции, которая заканчивается на шаге k=n)

начало

Очевидно, что этот алгоритм дает док-во утверждения P(n) для любого заданного n и тем самым мы получаем обоснование техники док-ва по методу МИ.

10. Примеры доказательств с использованием метода МИ.

Пусть задана последовательность чисел Фибоначчи 0,1,1,2,3,5,8,13,21,34,55,89…F(n)(каждое следующее число равно сумме двух

предыдущих)

Обозначим Ф 1 5 - золотое сечение.

2

Доказать что Fn≤Фn-1 (*) Доказательство: если n=1, то Fn=1

F1=Фn-1=Ф0=1 соотношение (*) выполняется для n=1.Тем самым выполнен пункт

Используя (***) и (**) получим F(n+1)≤Фn-2*Ф2=Фn, т.е. Fn+1≤Фn.Тем самым мы выполнили пункт б) .В данном доказательстве мы выполнили пункт б) двумя

разными способами:

1.Непосредственно доказали P(n+1) при n=1,т.е. доказали P(2)

2.Использовали предположение индукции при n>1 здесь мы были вынуждены так поступить, т.к. при n=1 ссылка на P(0)=P(n-1) была бы не законной, т.к. мы начинали доказательство с n=1, а не с n=0.