
матлогика - шпора
.pdf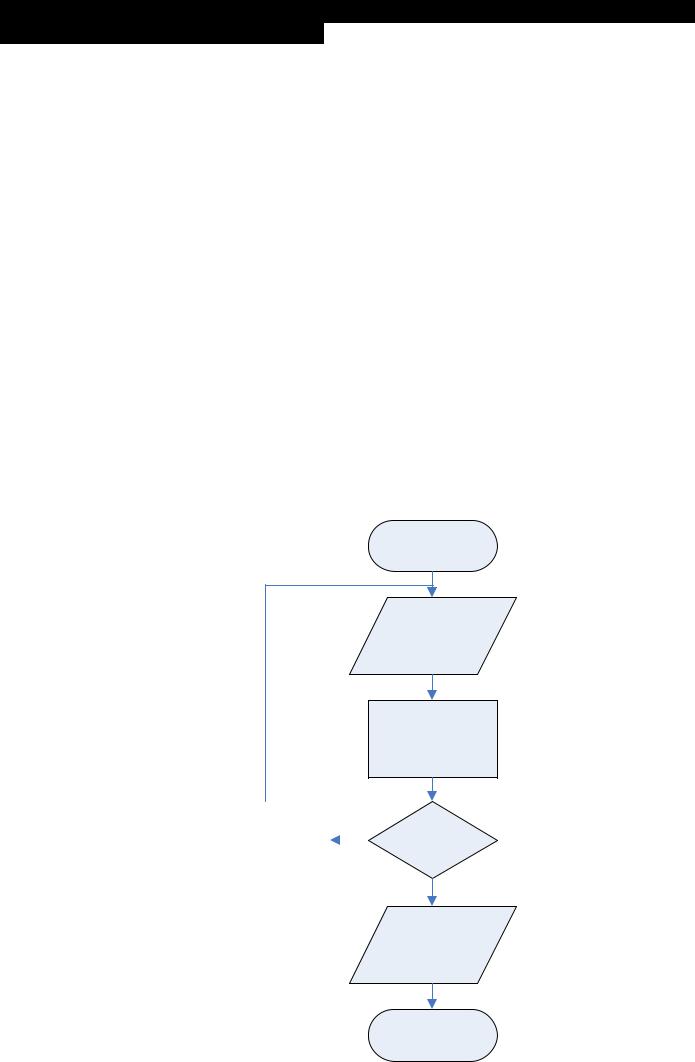
11. Использование метода МИ для исследования алгоритмов (на примере обобщенного алгоритма Евклида).
Приведем общий алгоритм Евклида (EV)
Даны два числа m и n – целые положит-ные числа. Найти d=нод и а, b такие что а*m+b*n=d
Алгоритм пошаговой записи EV1: [Начальная установка]
Положить а|←b←1; а← b|←0; c← m; d←n;
EV2: [разделить] Пустьq и ч являются соответственно: частное от деления c/d и остаток (имеем c=q*d+r, 0≤ч<d)
EV3: [r=0?] Если r=0, то алгоритм зак, раб, am+bn=d, если r≠0 то EV4
EV4: [Повторение цикла]
c← d; d← r; t← a|; a|←a; a←t-да; t←b|; b|←b; b←t-qb
Вернуться в EV2
Этот алгоритм похож на алгоритм Е, но дает больше возможностей, положит. коэффициент а,b.
Рассмотрим алгоритм Евклида для нахождения наибольшего общего делителя 2-х целых положительных чисел. Даны два целых положительных числа m и n.
Найти наибольший общий делитель: Ш1. [Нахождение остатка]
Разделим m на n. Пусть остаток равен r (У нас получится 0≤r≤n)
Ш2. [остаток равен 0?]. Если r=0, то алгоритм заканчивается и n-является наибольшим делителем
Ш3. [Замещение]. Положим m←n, n←r и вернемся на Ш1
НАЧАЛО
ввод m>0, n>0
ч←m mod n
m←n |
|
|
ч=0 |
n←ч |
|
|
|
|
|
|
|
|
|
|
|
да
n
используе
мый
результат
КОНЕЦ
Пример. Пусть m=1769, n=551, найти a и b. am+bn=d. d- это НОД. Выполним все установки и проследим, как будут изменяться все переменные в алг-ме после шага EV2
a‘ |
a |
b‘ |
b |
c |
d |
q |
r |
1 |
0 |
0 |
1 |
1769 |
551 |
3 |
116 |
0 |
1 |
1 |
-3 |
551 |
116 |
4 |
87 |
1 |
-4 |
-3 |
13 |
116 |
87 |
1 |
29 |
-4 |
5 |
13 |
-16 |
87 |
29 |
3 |
0 |
am+bn=d=5*1769-16*551=29=d, a=5, b=-16, d=29

12. Недетерминированные и детерминированные алгоритмы.
Недетерминированные (вводится для того, чтобы классифицировать более подробно задачи не попадающие ни в Р(«хорошая» задача для которой существует полиномиальный алгоритм) ни в Е(задачи экспоненциальные по своей природе) ) В общем случае определяет состояние алгоритма, как комбинацию адреса, выполняемой в текущей момент команды и значения всех переменных в данный момент. Алгоритмы называются детерминированными, если для любого их данного состояния существует не более 1-го следующего вполне определенного состояния. Иначе говоря, недетерминированный алгоритм, в любой момент времени может делать больше вещи.
Недетерминированные (Нд) алгоритмы не являются вероятными или случайными, они являются алгоритмами, которые могут одновременно находится во многих состояниях. Нд лучше всего понять, если рассматривать алгоритм который производит вычисление до тех пор, пока не доходит до места, в котором должен быть сделан выбор из нескольких альтернатив.
Детерминированный алгоритм исследовал бы одну альтернативу, затем возвращался бы для исследования другой альтернативы и т.д.
Нд алгоритм:
Может исследовать все альтернативы одновременно копируя себя для каждой альтернативы. Все копии работают независимо друг от друга. Эти копии могут создавать следующие копии, для дальнейшего исследования
алгоритмов. Если какая-то копия обнаруживает что она сделана неправильный или безрезультатный выбор она прекращает работу, если находит решение, она сообщает всем копиям о своем успехе и все копии прекращают работу.
 Очевидно, что никакое физическое устройство не способно на неограниченную Нд работу.
Очевидно, что никакое физическое устройство не способно на неограниченную Нд работу.
Детерминированный алгоритм (Дд)
Дд. алгоритмы являются абстракцией, которая позволяет игнорировать некоторые проблемы решения задач поиска с возвращением
Определяем класс NP как класс всех задач, которые можно решить Дд алгоритмами за полиномиальное время. Очевидно, что P NP т.к. путей может быть экспоненциально много, то алгоритмы, допустимые в этом случае намного сильнее, чем детерминированные алгоритмы, допустимые для задач класса Р.
NP-трудные и NP-полные задачи
Различные задачи, которые относятся и классу NP могут быть эквивалентными относительно некоторого отношения, которые определяем => обр.:
Опр. Задача Q полиномиально сводится к задаче R <=> выполн => условие
1.существует функция g(x) и f(x), вычисляемые за полиномиальное время
2.любого входа х частного случая задания Q значение g(x) является входом частного случая задания R
3.любые решения (выхода) у задания R значения f(y) является решением задачи Q Т.о. для решения одной задачи (в данном случае Q) используется алгоритм решения
другой задачи (в данном случае R)
Таким приемом часто пользуются при защите докторской диссертации Опр. Если одновременно задача Q полиномиально сводится к задаче R и R
полиномиально сводится к задаче Q, то Q и R полиномиально эквивалентны.
Опр. Задача называется NP – трудной (NP – сложной), если всякая задача из NP полиномиально сводится к данной.
Опр. Задача называется NP – полной, если она входит в NP и является NP – трудной
13. Разделы математической логики, представление операций булевой логики через множества и их отображение с помощью диаграмм ЭйлераВенна.
3 раздела:1. логика Буля 2. логика высказываний 3. Логика предикатов 1. Основываясь на отношении эквивалентности, при котором левая часть
равенства содержит столько же «истины», сколько и правая. При этом не происходит приращения нового значения.
2, 3. Основывается на отношении порядка, при котором правая часть выражения (вывод, заключение) содержит больше «истины», чем левая часть (посылка).Операции логики Буля удобнее всего объяснить через понятие множество. Определим множество, как совокупность объектов, поддающихся счету. Если счет продолжается бесконечно долго, то имеем бесконечное множество. Если же только начавшись сражу заканчивается, ввиду отсутствия объектов, то имеем пустое множество <= 2 крайних случая.Мы будем рассматривать конечное и непустое множество.
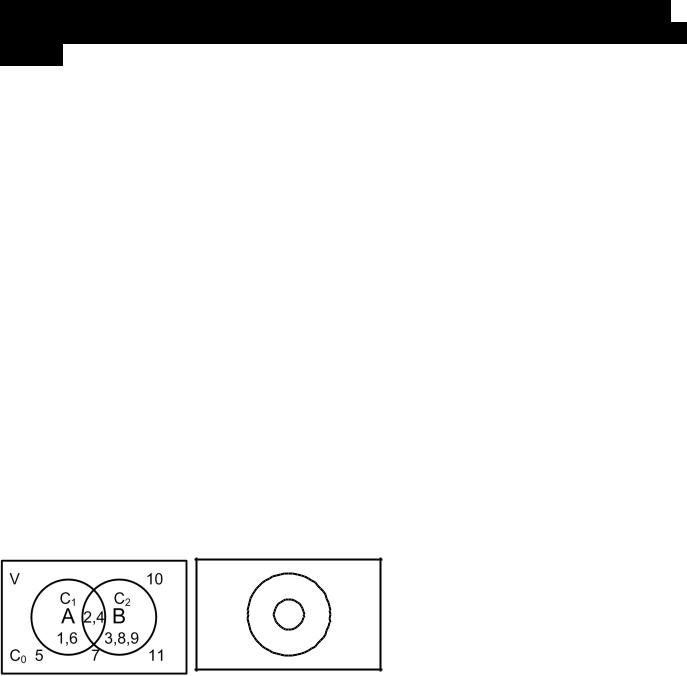
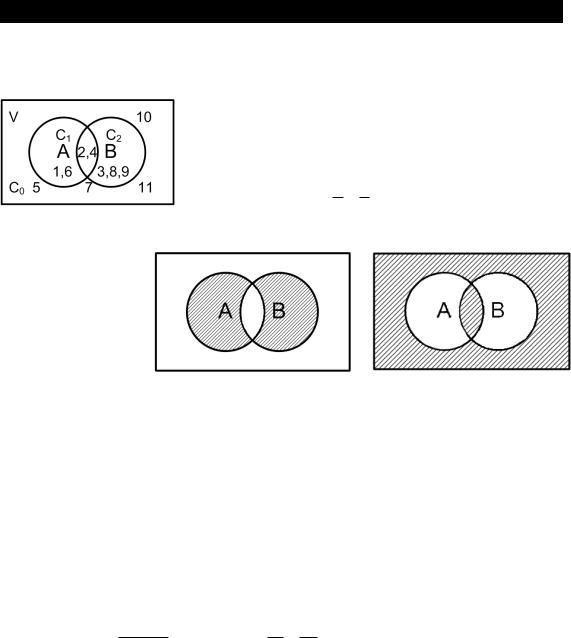
Пусть дана совокупность незаданных объектов, которые после пересчета можно представить V={1, 2, …,11}Предположим, что часть объектов А=1,2,4,6 – круглые; В=2,3,4,8,9 – белые. В этом случае говорят, что множество V имеет 2 подмножества А и В. Исходное множество V называется фундаментальным. Подмножества А и В – просто множествами. В примере имем 4 класса объектов.
С0={5,7,10,11} – те, которые не обладают ни одним из названных свойств. С1={1,6} – предметы, обладанием только свойством А.С2={3,8,9} – предметы, обладанием только свойством В. С3={2,4} – предметы, обладанием свойством А и В. Эти классы можно изобразить графически, с помощью диаграммы ЭйлераВенна
V
A B
Множество А полностью в В А В
- символ включения А В
иВ А, то А=В
А и В полностью эквивалентны

14. Объединение множеств и переход от предметной переменной х к логическим переменным Х1 и Х2 .
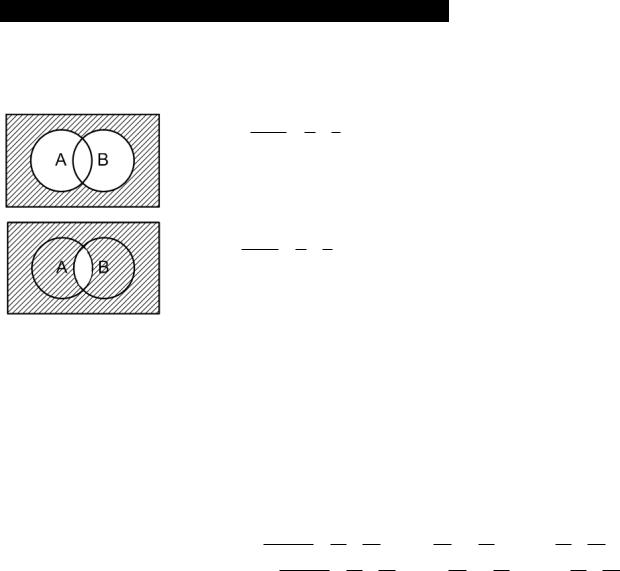
Объединением Ма U Мb двух множеств Ма и Мb является множество М, состоящее из элементов множества Ма и из элементов множества Мb. М= Ма U Мb = {mi/miЄ Ма, Мb}.Охватывают три класса объектов которые на диаграмме заштриховываются .Логически операцию объединения можно представить : объект ХЄА и/или В . то что ХЄА и/или В выражается : ХЄА U В=(XЄА)٧(ХЄВ) ,٧
-символ логичемской связки (дизъюнкция)
Для операций алгебры Кантора выполняются следующие законы:
Коммутативность объединения
Ма U Мb= Мb U Ма Ассоциативность объединения
Ма U( Мb U Мс)=( Ма U Мb) U Мс
Дистрибутивность пересечения относительно объединения и объединение
относительно пересеченияМа ∩ (Мb U Мс) = (Ма ∩ Мb) U (Ма ∩ Мс)
Ма U Мb Ма U (Мb ∩ Мс) = (Ма U Мb) ∩ (Ма U Мс)
объединения
универсальными 1 и пустыми Ø множествами
___
U 1 = 1, М U M = 1
|
|
____________ |
___ |
___ ____________ |
___ |
___ |
|
|
a M b |
M a |
M b , M a M b |
M a |
M b ; двойного дополнения |
___ |
___ |
|
|
|
|
|
M a |
M b |
M M Сточки зрения булевой логики вместо 1 предметной |
||||
переменной х вводим 2 логических переменных. Областью определения предметной переменной х-все числа натурального ряда, j входят в множество V. Область определения 2-х переменных х1, х2 являются 2 числа 0-лож, 1- истинаПример: Предположим, что часть объектов А=1,2,4,6 – круглые;
В=2,3,4,8,9 – белые.возьмем х=7 х1=0 х2=0 ; для х=6 х1=1 х2=0 ; для х=3х1=0 х2=1. Таким образом х1 и х2 определяют некоторую логическую функцию
которая св случае дизъюнкции запишется : у=х1 ٧х2

15. Пересечение множеств, тавтология, противоречие, дополнение и области взаимодействия двух множеств на диаграмме Эйлера-Венна.
Пересечение Ма ∩ Мb двух множеств Ма и Мb является множество М, состоящее из элементов, которые принадлежат как множеству Ма так и множеству Мb:
М= Ма ∩ Мb = {mi/miЄ Ма и miЄ Мb} союз ‗и‘ можно заменить знаком &
Для операций алгебры Кантора выполняются следующие законы:
Коммутативность объединения
Ма ∩ Мb= Мb ∩ Ма Ассоциативность объединения
Ма ∩ ( Мb ∩ Мс)=( Ма ∩ Мb) ∩ Мс Дистрибутивность пересечения относительно
объединения и объединение относительно пересеченияМа
∩(Мb U Мс) = (Ма ∩ Мb) U (Ма ∩ Мс)
Ма U Мb Ма U (Мb ∩ Мс) = (Ма U Мb) ∩ (Ма U Мс) Ма U (Мb ∩ Мс) = (Ма U Мb) ∩ (Ма U Мс)
Идемпотентность объединения
универсальными 1 и пустыми Ø множествами
|
|
___ |
|
|
|
М, М ∩ M |
= Ø |
|
|
|
____________ |
___ |
___ |
|
|
a M b |
M a |
M b ; |
|
____________ |
|
|
|
|
M a Mb |
двойного дополнения M |
M |
||
Тавтология – логическое выражение, которое всегда является истинным, вне зависимости от значения х.Противоречие – всегда ложное логическое
___
выражение, вне зависимости от х. A дополняет А до фундаментального
___
множества V, поэтому операция, которая позволяет получить не А, A
___
называется дополнением.Дополнением к логическим переменным x -
отрицание х

16. Таблицы истинности для дизъюнкции и конъюнкции.
Между таблицами истинности и диаграмм Эйляра-Венна существует взаимнооднозначное соответствие: количество единиц совпадает с количеством заштрихованных областей. Нетрудно посчитать что число всех возможных комбинаций 0 и 1 равно 16 (от 0000 до 1111) это означает что общее количество логических операций равно этому числу.
Общее количество логических операций для двух переменных 24 = 16. Для любой логической операции существует двойственная к ней.
Дизъюнкция
X1 |
X2 |
Y = X1 v X2 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Конъюнкция
X1 |
X2 |
Y = X1 ^ X2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
17. Операции стрелка Пирса и штрих Шеффера.
Эти операции дополняют объединение и пересечение до фундаментального множества соответственно.
На языке логических формул это записывается следующим образом:
Стрелка Пирса – это дополнение к объединению
A B = A B = A B
(X1 X2 ) (X1 X2 ) 1
(X1 X2 ) (X1 X2 ) 0
Штрих Шеффера – дополнение к пересечению
A B = A B = A B
(X1 X2 ) (X1 X2 ) 1
(X1 X2 ) (X1 X2 ) 0
Таблицы истинности |
|
|
|
|
|
||
|
Стрелка Пирса |
|
Штрих Шеффера |
||||
|
X1 |
X2 |
Y = X1 ↓ X2 |
|
X1 |
X2 |
Y = X1 | X2 |
|
0 |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
0 |
|
0 |
1 |
1 |
|
1 |
1 |
0 |
|
1 |
1 |
0 |
Из диаграмм Эйлера-Венна и таблице истинности видно:
Стрелки Пирса: Y = X1 X2 X1 X2 X1 X2 (X1 X2 ) X1 X2 X1 X2 Штрих Шеффера: Y = X1 X2 X1 X2 X1 X2 (X1 X2 ) X1 X2 X1 X2
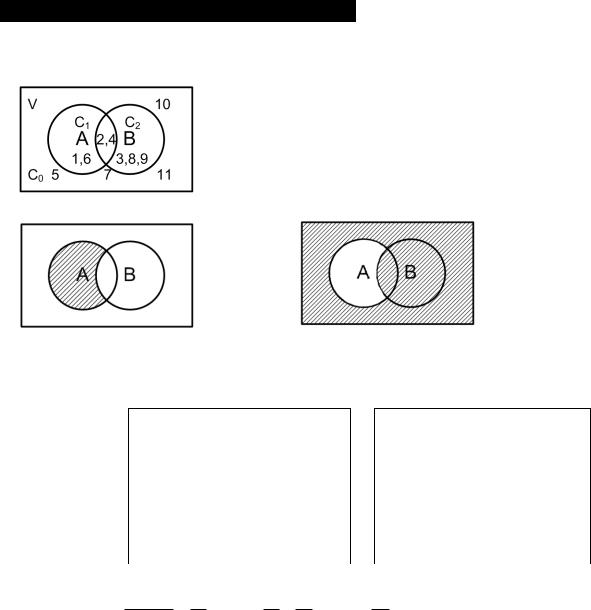
18. Операции разности и импликации.
Разностью множеств A и B, это множество, которое вошло в A, но не вошло в
B:
А – В = {1,2,4,6} – {3,4,8,9,2} = {1,6} = C1
Дополнение к разности называется импликацией |
|
- |
импликация |
A \ B (A - B)
Таблицы истинности:
Разность
X1 |
X |
Y = X1 - |
|
2 |
X2 |
||
|
|||
0 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
1 |
0 |
Для данных операций можно записать:
A → B
Импликация
X1 |
X2 |
Y = |
|
X1→X2 |
|||
|
|
||
0 |
0 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
Y = X1 X2 X1 X2 X1 X2 (X1 X2 ) X1 X2 X1 X2
(X1 X2 ) (X1 X2 ) 1
(X1 X2 ) (X1 X2 ) 0
19. Операции симметрической разности и эквивалентности.
Симметрическая разность двух множеств А и В – это объединение следующих двух разностей, то есть
А + В = (А - В) v (B - A) = {1,6} v {3,8,9}= {1,3,6,8,9} = C1 v C2
Дополнительной к данной операции является операция эквивалентности, которая определяется теми же элементами множества А и В, которые являются для них общими, при этом элементы не входящие ни в А ни в В также являются эквивалентными.
A B = (A ) A C0 C3 2, 4,5, 7,10,11
Симметричная разность |
Эквивалентность |
A + B |
|
|
A ~ B |
|
|
|
|
|
|
|
Разность |
|
|
|
Импликация |
||||
|
X1 |
X |
|
Y = X1 |
+ |
|
X1 |
X2 |
Y = X1 ~ |
|
2 |
|
X2 |
|
|
X2 |
|||
|
|
|
|
|
|
|
|||
|
0 |
0 |
|
0 |
|
|
0 |
0 |
1 |
|
1 |
0 |
|
1 |
|
|
1 |
0 |
0 |
|
0 |
1 |
|
1 |
|
|
0 |
1 |
0 |
|
1 |
1 |
|
0 |
|
|
1 |
1 |
1 |
Симметричную разность имеет другие названия: строгая дизъюнкция, исключительная альтернатива, сложение по модулю.
Из определения операции симметричной разности и эквивалентности следует:
Y = X1 X2 X1 X2 (X1 X2 ) X1 X2 (X1 X2 ) (X1 X2 ) 1
(X1 X2 ) (X1 X2 ) 0
