
матлогика - шпора
.pdf
20. Формы представления булевых функций (СДНФ, СКНФ, СПНФ).
Любую булеву функцию y=f(a,b) можно представить как комбинацию
|
|
= |
|
|
|
|
|
|
|
|
|
c |
0 |
a |
b |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
= a b |
Êî í ñò èí ò óåí ò û |
|||||||||
областей: c2 |
|
|
|
|
|
|
|
|
|
||
= a b |
|
||||||||||
c3 |
|
|
|
|
|
|
|
|
|
|
|
= a b |
|
||||||||||
Тогда в зависимости от значения функций и заданных ci ,i 1,3 , которые
именуются констинтуентами, получим 16-ть конечных операций, которые в общем виде можно записать:
y = [a b f(0,0)] a b f(1,0) a b f(0,1) a b f(1,1)
Такая форма представления называется СДНФ (совершенно-дизъюнктивная нормальная форма)
Вней констинтуенты – коньюнты соединяются с помощью дизъюнкции.
Влогике Буля действует принцип двойственности, который говорит, если одновременно заменить все конъюнкции на дизъюнкции, или наоборот (все ^ на v), замене символов (конъюнкция на дизъюнкцию и 0 на 1), то все логические равенства остаются в силе.
y = [a b f(1,1)] a b f(0,1) a b f(1,0) a b f(0,0)
Такая форма представления логических функций называется СКНФ (совершенная коньюктивная нормальная форма). В ней констинтуенты – дизъюнкты, соединяются с помощью конъюнкции.
Существует также третья форма представления логических функций СПНФ – совершенная полиномиальная нормальная форма. Ее можно получить из СДНФ путем следующей замены:
a b = a+b+ab; a =1+a; b =1+b
Так как СДНФ все констинтуенты не пересекаются, то можно записать: y = [(1+a)(1+b)f(0,0)]+[a(1+b)f(1,0)]+[(1+a)bf(0,1)]+[abf(1,1)] =
= f(0,0)+a[f(0,0)+ f(1,0)]+b[f(0,0)+ f(0,1)]+ab[f(0,0)+ f(0,1)+ f(1,0)+ f(1,1)]
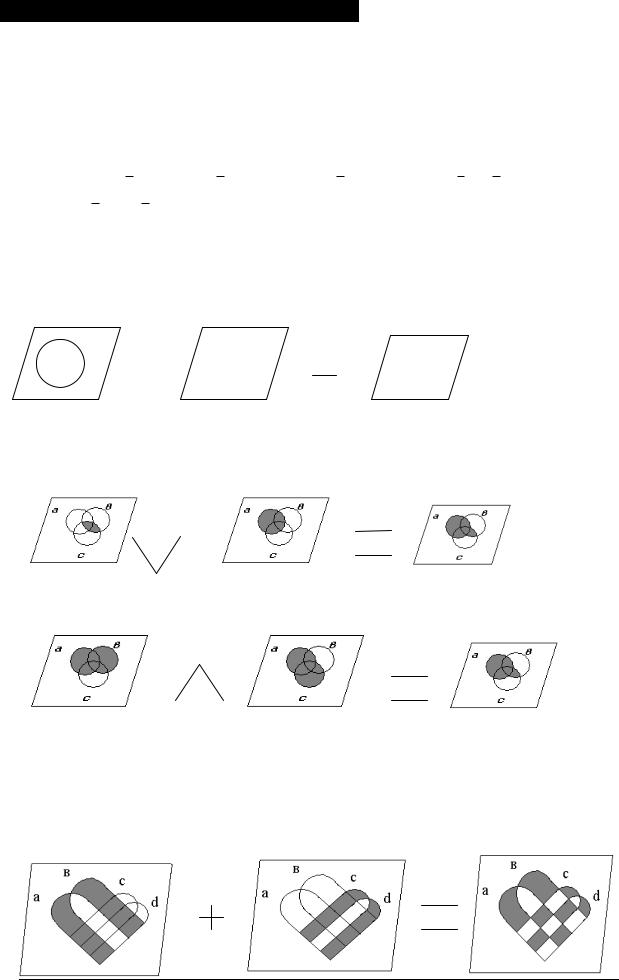
21. Двойственность в булевой логике.
1.аксиоматический
2.конструктивный
1)При использовании 1 используется т-мы аксиом из преведенных 4 законов. Все остальные тождества можно доказать через эти законы.
2)Метод констуктов, примерами являются диаграммы Эйлера-Венна и таблиц истиности.
Дано простое тождество: a 0 0
a 0 a (a a) (a a) a ((a a) 0) a ((a a) (a a)) a(a 1) a a a 0
Эти преобразования проводятся для того что бы формально-привязаться к объявленной систем аксиом. Для конструктивности
Тождество выглядит очевидным и не требует доказательства. Противоположный случай произойдет и отношении закона диструктивности.
Аксирматик не предпринимает ни каких
a 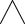
 действий, т.к. данный закон является аксиомой, а конструктивный должен
действий, т.к. данный закон является аксиомой, а конструктивный должен
должен продемонстрировать эквивалентность левой и правой частей тождества. а в с а в а с
Левая часть
в с |
а |
правая часть |
|
а в |
|
|
|
|
|
|
а с |
|
|
1 3 |
|
2 |
|
7 |
|
4 |
6 |
5 |
|
а в с d ((а ~ в) |
с d ) |
|
(а в / с |
d ) |
|||||
|
|
|
|
|
|
|
|
|
|
Левая часть
Правая часть
|
|
|
|
с d |
|
а ~ в |
с d |
а ~ в |
|
|
|
|
|
|
|
|
|
|
с d |
(*) |
|
а ~ в |
|
а ~ в |
||
|
|
|
|
|
|
а в | (c d) а в с d
(*) (**) =
(**)
Ч.т.д.
В правильности результата можно убедиться с помощью таблицы истинности:
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
а |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а+в |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а+в+с+ |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1= а ~ в |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f3= |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1→(c+d) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f6 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f7 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а+в+с+d—fлевое f7—fправое |
|
fлевое= fправое (ч.т.д.) |
|
|
|
||||||||||||
Второй способ док-ва через таблицы истинности. |
|
|
|
|
|
||||||||||||
Существует также обратная задача,по существующей диаграмме.Найти аналитическое выражение.
Пусть дана
найти выражения с1= а в с ; с2 а в с
у с1 с2 а в с а в с в а в с а с в а с

22. Различия отображения логических функций в СДНФ. СКНФ и СПНФ. Переход из СДНФ в СПНФ.
Третья формула представления СПНФ (совершенная номинальная нормальная форма). Ее можно получить из СДНФ в результате следующих замен:
а в а в ав здесь ав а в и а 1 а ; в 1 в .
успнф 1 а 1 в f 0,0 а 1 в f 1,0 1 а вf 0,1 авf 1,1
Констинтуенты не пересекаются
= f 0,0 а f 0,0 f 1,0 в[ f 0,0 f 0,1 ] ав f 0,0 f 1,0 f 0,1 f 1,1
ВСДНФ за основу берут единицу. Переменные в скобках объединяются (по принципу если x1=1 , то х1, если х1=0 , то х1 ) законом коньюнкции, а между скобками ставится знак дизьюнкции.
ВСКНФ за основу берут единицу. Переменные в скобках объединяются (по
принципу если x1=0 , то х1, если х1=1 , то х1 ) законом дизьюнкции, а между скобками ставится знак коньюнкции.
В СПНФ - x 1 x и на + получаются из СДНФ.

23. Минимальные нормальные формы логических функций.
умднф (минимизируемая конъюнкция нормальная
форма)= (х3 х1 ) х2 х1 х3 х2 х1 .
Приведем полный список элементарных логических функций от 2-х переменных, представленных в 3-х совершенных формах: СДНФ, СКНФ, СПНФ-всего 16.
|
у f а, в |
СДНФ=СКНФ=СПНФ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0000 |
у0 |
0 |
а в |
|
|
|
|
|
|
в а в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
а |
в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0001 |
у1 |
а в |
а в а в |
|
|
|
|
|
в а |
|
|
|
|
|
|
|
ав |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0010 |
у2 |
в а |
|
|
|
|
|
|
|
|
|
|
в а в |
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в ав |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
а |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0011 |
у3 |
в |
|
|
|
в а в а в |
|
|
|
|
|
|
|
|
в в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
0100 |
у4 |
а в |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а в а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а а в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в |
в |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
0101 |
у5 |
а |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а в а в а |
|
|
|
|
|
|
|
а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
0110 |
у6 |
а в |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в а в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в |
а |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
0111 |
у7 |
а в |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в а в а в а в ав |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в |
а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
1000 |
у8 |
а в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 а в ав |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
в |
а |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1001 |
у9 |
а ~в |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) а в |
|
|
|
в а |
|
|
|
|
|
|
|
|
1 а в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1010 |
у10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
в |
|
|
|
|
|
|
|
|
1 а |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
|
а |
в |
а |
а |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1011 |
у11 а в |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
в а в |
|
|
|
|
|
|
|
|
в 1 а ав |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
а |
а |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1100 |
у12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 в |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в |
|
а |
в |
в |
в |
а |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1101 |
у13 в а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
а в а |
|
|
|
|
|
|
|
1 в ав |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
в |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1110 |
у14 а / в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
â |
|
|
|
|
|
|
|
|
1 àâ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
à |
â |
â |
à |
à |
â |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1111 |
у15 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
а |
|
|
|
а в 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а |
в |
в |
в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представление функции в СКНФ и СДНФ образуются 3 одинаковыми операциями:
1.дизъюнкция
2.конъюнкция
3.отрицание
В СПНФ:
1.сложение по модулю 2
2.конъюнкция
3.1, как и логическая операция

24. Принцип суперпозиции в булевой логике и приоритеты логических операций.
Принцип суперпозиции.
Каждая сложная функция может быть представлена в виде совокупности элементарных логических функций от 2-х переменных.
3 |
5 |
4 |
|
1 |
2 |
|
# f (x1, x2, x3, x4) ((x1| x2) |
(x2 |
x3)) |
(x x4) |
|
||
(x1 x2 x3 x4) (x1 x2 x3 x4) (x2 x3 x4) (x4 x3) x2
(цифры над знаками логических функций есть номер порядка выполнения этих знаков)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
X1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
X2 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
X3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
X4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
2 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
3 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
25. |
Классы элементарных логических функций. |
|
|
|
|||||||
Определяется следующие 5 классов: |
|||||||||||
0 |
– класс: Функции, которые сохраняют нулевое значение на нулевом наборе |
||||||||||
терминов, то есть f (0;0) 0 к этому классу относится все функции f0 f7 |
|||||||||||
1 |
– класс: Все функции, которые имеют значение 1 на единичном значении |
||||||||||
термов, то есть f (1;1) 1 . К 1 классу относятся все нечетные функции. |
|||||||||||
2 |
– класс: Класс линейных функции – все функции, у которых в полиномиальном |
||||||||||
представлении нет слагаемого a b . |
|||||||||||
3 |
– класс: Класс самодвойственных функций – функции, для которых выражается |
||||||||||
|
|
|
|
|
|
|
|||||
соотношение: f (a,b) f (a,b) и четыре f a , f a , f b , f b . |
|||||||||||
4 |
– класс: Класс монотонных функций – функции, для которых выражается |
||||||||||
неравенство: f (a,b) f | (a| ,b| ) , если a a| , b b| .
Приведем таблицу принадлежности логических функций тому или иному классу.
k |
f0 |
f1 |
f 2 |
f3 |
f 4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
2 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
3 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
4 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Зададим: 1 – f принадлежит некоторому классу 0 – f не принадлежит некоторому классу
26. Законы логики Буля.
1.a 1 a a 0 1 a a ~ 0 a | a a a 2.a b a b a ~ b a ~ b a ~ b
3.a b a b
4.1a a a a a ~ a
5.0a a a a a a
6.a b (a | b) | (a | b) (a a) (b b) (a b)
7.a b (a b) (a b) (a | a) | (b | b) (a b)
Существует 2 подхода к доказательству:
1.аксиоматический .
2.конструктивный
а) идемпотентности: а=а∩а; а=аUа
б) коммутативности: а∩b=b∩а; аUb=bUа
в) ассоциативности: (a∩b) ∩c=a∩(b∩c) ; (aUb) Uc=aU(bUc)
г) дистрибутивности: a∩(bUc)=a∩bUb∩c ; aU(b∩c)=(aUb) ∩ (aUc)
д) законы нуля и единицы: a a 0;a a 1;a 1 a;a 0 a;a 1 1;a 0 0. е) законы поглощения: aU(a∩b)=a; a∩(aUb)=a
7. Законы де Моргана: a b a b
a b a b
8. Законы склеивания: (a b) (a b) a
(a b) (a b) a
Не все 8 законов независимы друг от друга Например закон идемпотентности может быть получен из закона поглощения с использованием закона дистрибутивности.
Закон поглощения
а=аU(а∩b)=(aUa) ∩ (aUb)=(a∩ (aUb))(a∩ (aUb))=aUa 1)aUa=a
Закон поглащения может быть выведен из закона 0 и 1
аU(a∩b)=(a∩1)U(a∩b)=a(1Ub)=a∩1=a
Законы идимпотенции относительно дизъюнкции, т.к. можно вывести из закона 0 и 1
аUа=(аUа) ∩1=(аUа) ∩ (аU a )= а ∩ (аU a )=аU0=а
При доказательстве логических выражений нужно иметь в виду достойность логики Буля Закон поглощения:
a∩ (aUb)=(aU0) ∩ (aUb)=aU (0∩b)=aU0=a
В качестве независимой системы аксиом используется следующие законы: -коммутативности; -ассоциативности; -дистрибутивности; -закон 0 и 1;

27.Применение закона поглощения для нескольких переменных.
{Закон поглощения av(aΛb)=a; aΛ(aΛb)=a;}
Упростим сложное высказывание: (А + В)•(А + В + С) = A•A + A•B + А•С + А•В
+• + В•С; В соответствие с законами булевой алгебры, А•А всегда равно 0, а • всегда равно В. Группируя теперь второй и пятый члены развѐрнутого выражения, получаем: В•(А+1) + А•С + А•В + В•С; А+1 всегда равно 1, поэтому объединяем теперь первый и третий члены полученного выражения: В•(1+А) + А•С + В•С; Далее группируем снова первый и третий члены выражения: В•(1+С) + А•С = В + А•С, что и требовалось доказать.
Можно осуществить решение проще, воспользовавшись законом поглощения В + Х•В = В, где Х - любая логическая переменная. Перепишем развѐрнутое выражение с учѐтом того, что А•А равно 0 и • равно В: А•В + А•С
+А•В + В + В•С; Переменная В последовательно поглощает первый, третий и пятый члены выражения, в результате остаѐтся А•С + В.
28. Аксиоматический подход к доказательству логических выражений в булевой
Опирается на следующие законы логики Буля: а) идемпотентности: а=а∩а; а=аUа
б) коммутативности: а∩b=b∩а; аUb=bUа
в) ассоциативности: (a∩b) ∩c=a∩(b∩c);(aUb) Uc=aU(bUc)
г) дистрибутивности: a∩(bUc)=a∩bUb∩c;aU(b∩c)=(aUb) ∩ (aUc)
д) законы нуля и единицы: a a 0;a a 1;a 1 a;a 0 a;a 1 1;a 0 0.
е) законы поглощения: aU(a∩b)=a; a∩(aUb)=a
при использовании аксиоматического подхода используются системы аксиом из приведенных 4 законов. Все остальные тождества можно доказать через эти законы. Дано простое тождество: а∩0=0
а∩0=а∩ (а∩ a )=(а∩а) ∩ a =((а∩а) U0) ∩ a =((а∩а) U (а∩ a ))∩ a =(а∩ (аU a ))∩ a =
=(а∩1) U a =а∩ a =0 эти преобразования проводятся для того чтобы формально привязать к объявленной системе аксиом.

29. Доказательство логических выражений с помощью диаграмм Эйлера-Венна.
((a | b) | (a ~ b)) | ((c d) (d c)) ((b c) (a c)) ((a | d) | (d b))
а|b |
ab |
1 |
→ |
|
|
c+d |
d-c |
2 |
Левая часть. |
|
|
1|2
b→c |
a-c |
3 |
|
|
|
|
|
a|d |
d b |
4 |
||
3↓4
