3 Анализ зубчатых механизмов

Зубчатые механизмы (передачи) классифицируются на пространственные и плоские (см.1.5.2).

Пространственные механизмы – это передачи с пересекающимися (конические) или перекрещивающимися (червячные) осями колес.

Плоские зубчатые механизмы – это передачи с параллельными осями колес.

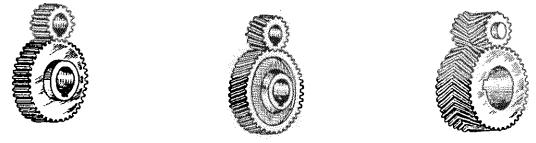
К ним относятся (рисунок 3.1):

Рисунок 3.1

а) цилиндрическая прямозубая; б) цилиндрическая косозубая (β = 80…250, одно колесо левое, второе –

правое); в) шевронная, т.е. сдвоенная косозубая передача с противоположным

наклоном зубьев (β = 250…400);

3.1 Основной закон зацепления (теорема Виллиса)

Зубчатые колеса представляют собой звенья, имеющие по окружности выступы (зубья), чередующиеся со впадинами. Число зубьев – Z. При передаче движения зубья одного колеса входят во впадины второго. Рабочими гранями являются боковые профили зубьев.

Отношение угловой скорости ω1 к ω2 называется передаточным отношением

i12 = ± ω 1 / ω 2 .

Рисунок 3.3

Рисунок 3.2

Рисунок 3.4

Знак учитывает направление вращения ведомого колеса по отношению к ведущему: для внешнего зацепления

i12 = − ω 1 / ω 2 ,

для внутреннего

i12 = + ω 1 / ω 2 .

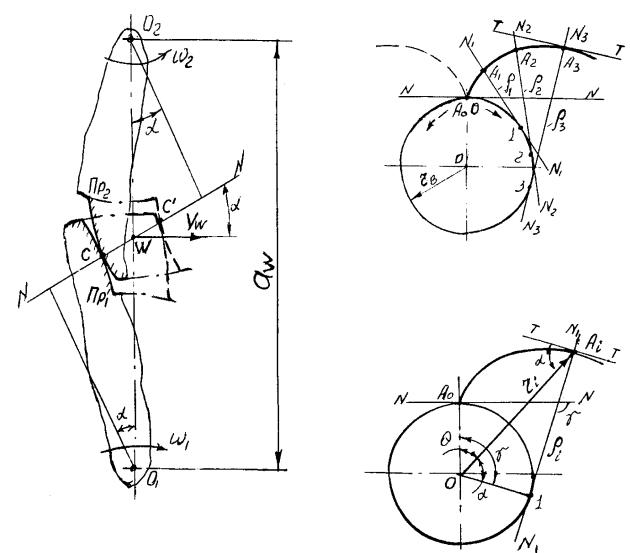
Расстояние между осями вращения О1 и О2 называется межосевым расстоянием aw (рисунок 3.2).

Пусть профиль Пр 1 звена 1 вращается с угловой скоростью ω1 вокруг неподвижного центра О1 и сообщает профилю Пр 2 звена 2 угловую скорость ω2 вокруг неподвижного центра О2.

Проведем через точку С касания профилей общую к ним нормаль NN. Эта нормаль пересекает линию центров. Точка пересечения является

мгновенным центром относительного вращения звена 1 относительно звена 2

– - Р12 (или Р21). В теории зацепления она называется полюсом зацепления и обозначается – W.

Линейная скорость полюса зацепления

VW = ω 1 O1 W = ω 2 O2 W ,

или

ω 1 / ω 2 = O2 W / O1 W = i12 .

Таким образом, чтобы получить определенное передаточное отношение, необходимо для профилей зубьев выбирать такие кривые, у которых общая нормаль NN, проведенная через точку касания С разделяла межцентровое расстояние О1О2 на части, обратно пропорциональные угловым скоростям.

Если i12 = const , то нормаль NN должна быть неподвижна, а полюс

зацепления W не менять своего положения на линии центров О1О2, в этом случае имеют место круглые колеса. Наибольшее распространение получили круглые зубчатые колеса, боковые профили зубьев которых очерчены по эвольвенте.

3.2 Теория эвольвенты

Эвольвентой или разверткой окружности называют плоскую кривую А0Аi, которая описывается любой точкой прямой NN, перекатываемой без скольжения по окружности (рисунок 3.3).

Линию NN называют производящей прямой, а окружность радиуса rв, по которой она перекатывается – эволютной, или основной окружностью.

Мгновенный центр вращения производящей прямой находится в точках 1, 2, 3. Поэтому точки 1, 2, 3 … являются центрами кривизны.

Отрезки ρ1 = A11 = A0 1, ρ2 = A0 2 = A2 2,ρ3 = A0 3 = A3 3

радиусы кривизны эвольвенты.

Отсюда следует:

- касательная, проведенная через любую точку на эволюте является нормалью к эвольвенте;

-длина этой касательной равна длине окружности от начала эвольвенты до рассматриваемой точки;

-эвольвенты, построенные на одной эволюте будут равноудаленными или эквидистантными, т.е. расстояние между ними по любой нормали одинаково и равно.

Рассмотрим основные параметры эвольвенты. Возьмем на эвольвенте

любую точку Аi и проведем через нее касательную NN к основной окружности (рисунок 3.4). Угол развернутости эвольвенты между нормалями

вначальной точке О (NN) и рассматриваемой точке 1 (N1N1).

Текущий радиус-вектор эвольвенты ri = OA i = rв /cosα .

Полярный угол эвольвенты или эвольвентный угол, определяющий направление текущего радиуса-вектора

Из свойств эвольвенты вытекает, что нормаль А1С к профилю А0А в точке касания С должна быть касательной к основной окружности rb1. А нормаль А2С к профилю В0В касательной к основной окружности rb2. Так как в точке касания двух кривых можно провести только одну общую нормаль NN, то отрезки А1С и А2С является участками общей нормали NN, которая одновременно касается обеих основных окружностей и пересекает линию центров в (. ) W. При повороте ведущего профиля А0А вокруг центра О1 ведомый профиль В0В будет поворачиваться вокруг центра О2, а точка контакта профилей С перемещаться.