0,34; 0,14; 0,02.
Сумма этих трех значений равна 0,5. Это значит, что для нормально распределенной случайной величины все рассеивания (с точностью до долей процента) укладывается на участке Mx±3σ.
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал её практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма». Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения σ.
Выборочные параметры являются случайными величинами, их отклонения от генеральных совокупностей (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Расчет границ доверительного интервала для математического ожидания случайной величины Х, распределенной по нормальному закону при неизвестном среднем квадратическом отклонении, выполняется по следующим этапам:
Для выборки значений случайной величины X с нормальным законом распределения рассчитываются несмещенные точечные оценки математического ожидания
при i=1,2,3…n,
и среднего квадратического отклонения
при i=1,2,3…n,
Затем, так как на практике, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия σ2 неизвестна, поэтому для построения доверительного интервала математического ожидания используют выборочную дисперсию s2 и приведенную случайную величину t. Где t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы l=n-1 (t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению.
Границы доверительного интервала по методу Стьюдента определяется следующим образом:
,
где t2(1-α/2,n-1)=-t1(α/2,n-1) – табличное значение зависящее от α=(1-P) и степеней свободы n-1, значения tα даны в приложении А, (таблица 2).
Порядок проведения работы
1. Используя пакет Microsoft Excel, построить зависимость случайной величины X от количества опытов n (рисунок 3.4).
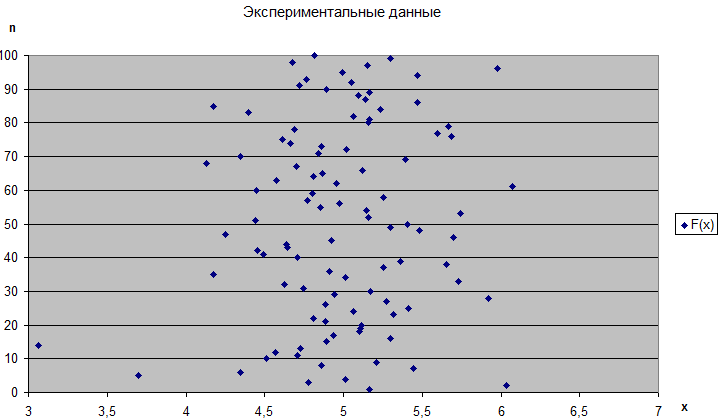
Рисунок 3.4 – Зависимость Х от n
2. Определить математическое ожидание Mx и дисперсию σ2 случайной величины X.
3. Записать функцию плотности распределения X.
4. Рассчитать вероятность попадания случайной величины X в интервал от α до β.
5. Рассчитать с помощью метода Стьюдента доверительный интервал для математического ожидания Mx случайной величины X.
4. Используя пакет Microsoft Excel, построить функцию плотности распределения случайной величины X, с обозначением на ней Mx, σ, 2σ, 3σ и доверительных интервалов для центра рассеивания Mx для двух различных значений вероятностей (рисунок 3.5).
Рисунок 3.5 – Функция плотности распределения X
Для построение функции плотности распределения сначала необходимо провести ранжирование случайной величины X т.е. выстроить в порядке убывания и добавить крайние значения величины X (ближайшее минимальное целое и ближайшее максимальное целое число данная операция представлена на рисунке 3.6) после чего вычислить функцию плотности распределения от случайной величины X.
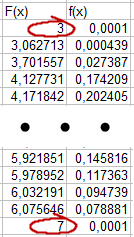
Рисунок 3.6 – Ранжирование результатов эксперимента и добавление крайних значений
4. Составить выводы.