Лекции по метрологии. Часть 4

1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА ПРИКЛАДНОЙ ФИЗИКИ

На правах рукописи

А.М. Чмутин

ЛЕКЦИИ ПО МЕТРОЛОГИИ

Волгоград

2005

2

3

Приложение E

Обработка результатов измерений методом наименьших квадратов.

При проведении математической обработки результатов измерений задача формулируется, как нахождение некоторой функции у=f(x), значения которой при х=x1, x2, ... xn возможно меньше отличались бы от опытных значений у1, у2, .... уn.

Стоит сразу же предупредить, что метод наименьших квадратов отнюдь не позволяет выявить из результатов измерений вид f закономерности изменения измеряемой величины. Применение метода наименьших квадратов дает возможность лишь подтвердить или опровергнуть догадку о виде этой функции. Геометрический же смысл задачи заключается в проведении плавной кривой y=f(x), проходящей наиболее близко к опытным точкам.

Линейная задача наименьших квадратов предполагает допустимость аппроксимации опытных точек линейной зависимостью f(x, а, b, с, ... m) от параметров а, b, с, ... m.

Если, например, в качестве функции f(x) взят полином порядка m

то метод наименьших квадратов позволяет найти такие значения параметров а, b, с, ... m, при которых сумма квадратов отклонений расчетных значений f(x1), f(x2), … f(xn) от опытных у1, y2, … f(xn) была бы наименьшей, т.е. чтобы выбранные значения параметров полинома давали наименьшую величину

n

S= [y1-f(xi)]2

i 1

где [уi-f(xi)] - отклонение по ординате опытной точки от соответствующей точки искомой кривой.

С учетом выражения (EI) формулу для S можно записать так:

i 1

Для выполнения этого условия (минимизации S) достаточно приравнять нулю все частные производные (Е2) по параметрам a, b, c, … m:

4

Полученная система (Е3) из (m+1) уравнений позволяет найти значения всех неизвестных параметров, которые вычисляют следующим образом.

1. По опытным данным составляют условные уравнения:

где значения x и у берут из опытных данных, причем число n уравнений больше числа m неизвестных.

2. Составляют нормальные уравнения, для чего:

а) умножают каждое условное уравнение на коэффициент при а (он равен х°=1), складывают их и находят первое нормальное уравнение

a+bx1+cx12+…+mx1m=y1 a+bx2+cx22+…+mx2m=y2

…………………………..

a+bxn+cxn2+…+mxnm=yn

--------------------------------

б) умножают каждое условное уравнение на коэффициент при b и находят второе нормальное уравнение

ax1+bx12+cx13+…+mx1m+1=y1x1 ax2+bx22+cx23+…+mx2m+1=y2x2

…………………………… …. axn+bxn2+cxn3+…+mxnm+1=ynxn

5

в) умножают каждое условное уравнение на коэффициент при с и находят третье нормальное уравнение

Затем умножают каждое условное уравнение на коэффициенты при прочих искомых параметрах и находят оставшиеся нормальные уравнения. Всего будет m нормальных уравнений, т.е. столько, сколько имеется неизвестных параметров.

3. Решая полученную систему нормальных уравнений

находят искомые параметры а, b, с, ... m и получают эмпирическую формулу

4.По формуле (Е4) определяют значения у1э=fэ(x1).

5.Находят невязку εi как разность между значениями уi полученными из опыта, и уiэ, найденными по формуле (Е4):

εi=yi-yiэ

6.Зная невязку, уточняют значения искомых параметров, ко-

торые принимают равными А=а+α; В=b+β; С=с+ ; ... М=m+μ, где поправки α; β; ; … μ находят следующим путем.

7. Составляют новые условные уравнения того же вида, что и

ранее

8. Как и прежде составляют нормальные уравнения умножением каждого условного уравнения на множитель при , затем при β и т.д., после чего полученные выражения складывают и получают систему новых нормальных уравнений.

6

9. Решают полученную систему нормальных уравнений относительно поправок α; β; ; … μ.

10. По найденным поправкам и вычисленным в п. 3 параметрам а, b, с, ... m находят исправленные искомые параметры А; В; С;

... М, после чего исправляют эмпирическую формулу, которая теперь принимает вид

Удовлетворительность проведенной аппроксимации проверяют путем вычисления среднего квадратического отклонения опытных значений у1, y2, ... yn величины уi от результатов F(x1), F(x2),

...F(xn), полученных по эмпирической формуле (Е5). При этом должно соблюдаться неравенство

где n - число условных уравнений, равное числу значений х и у по результатам опыта; m - число определяемых параметров; y - допустимая погрешность измерений величины у при проведении опыта в долях y [71; 72; 73].

Итак мы показали, как метод наименьших квадратов позволяет найти эмпирическую формулу, обеспечивающую минимальную дисперсию отклонений точек (вычисленных по этой формуле) от экспериментальных. Как следствие, метод наименьших квадратов может быть эффективен для выявления закономерности изменения измеряемой величины при вариации условий проведения измерений; анализа трендов систематической погрешности измерений и т.д. [71].

Представляет интерес рассмотреть частный случай применения метода наименьших квадратов. Произведем статистическое оценивание результатов измерения постоянной величины – соответствующие выкладки студентам предлагается сделать самостоятельно, итоговая оценка есть среднее арифметическое результатов измерения этой величины [74].

ПРИМЕР I. при исследовании геометрической формы склейки из нескольких линз длиной 40 мм в пяти ее сечениях были получены

7

следующие отклонения от номинального значения диаметра d=20 мм:

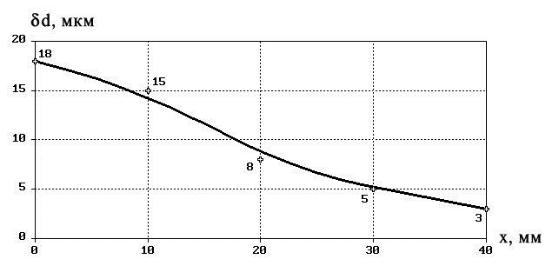
По этим данным построен график, представленный на рис. Е1.

Рис. E1. Отклонения диаметра d в разных сечениях склейки.

Требуется установить закономерность отклонений от правильной цилиндрической формы склейки по длине. При этом средняя квадратическая погрешность использованного метода измерения диаметра составляет σd =1,2 мкм.

Для решения этой задачи воспользуемся способом наименьших квадратов, с помощью которого найдем зависимость между x и δd, т. е. представим δd как функцию x. Исходя из графика, приведенного на рис. E1 и опираясь на опыт технологической практики, искомую функцию можно представить в виде полинома 1-го порядка:

di a bxi

где δdi - отклонение диаметра склейки от номинального значения 20 мм в i-м сечении xi - расстояние от торца до i-го сечения.

8

Для того, чтобы найти коэффициенты а и b, составим условные уравнения:

и нормальные уравнения:

Решая систему двух нормальных уравнений, находим значения искомых коэффициентов

a=(49-100b)/5; b=(580-100∙49/5)/(3000-1002/5);

откуда b=-0,4 и а=17,8.

Следовательно, искомая эмпирическая формула, выражающая зависимость между δd и х, будет иметь вид:

d 0,4 x /17,8

Найдем среднюю квадратическую погрешность отклонения опытных данных от результатов вычислений по найденной эмпирической формуле. Согласно равенству (E6) получим

Полученное значение =1,09 мкм не превышает равной 1,2 мкм средней квадратической погрешности использованного метода, т.е. находится в пределах точности измерений. Следовательно, найденная эмпирическая формула с точностью измерений отражает закономерность вариации геометрической формы исследуемой склейки, которая определяется как конусность [71].

Мораль: после решения линейной задачи наименьших квадратов для обработки результатов проведенных с заданной точностью измерений диаметра склейка утверждать, что у нее выявлено наличие конусности можно уже обоснованно, а не умозрительно, что особо ценится в экспертных приложениях метрологии.

9

Нелинейная задача наименьших квадратов подразумевает невозможность аппроксимаций опытных точек линейной зависимостью f(х, а, b, с, … m) от параметров a, b, c, … m.

Часто из физических или каких-либо других соображений следует, что зависимость y=f(x) между величинами у и х должна хорошо описываться моделью вида y=g(x, а), где функция

g(x, a) g(x,a0 , a1 ,...,am )

нелинейно зависит от параметров а0, a1, … am.

Пусть функция y=f(x) задана таблицей значений y1=f(x1), i= 0, 1, ... n, где n»m. Тогда применение критерия наименьших квадратов приводит к задаче определения искомых параметров а0, a1, … am из условия минимума функции

n

s(a, y) (g(xi , a) yi )2

i 0

Нелинейная задача наименьших квадратов (особенно при большом числе параметров) весьма трудна для традиционной технологии - аналитического решения. Обычно для вычисления параметров а применяются специальные методы минимизации.

В некоторых весьма специфических случаях решение линейной задачи наименьших квадратов можно свести к решению линейной задачи. Пусть, например, зависимость у от х ищется в виде y=a∙exp(bx), где а>0. Логарифмируя это равенство, приходим к линейной зависимости lny=lna+bx величины Y=lny от x. Теперь по таблице значений Уi=lnуi (i=0, 1, … n) можно легко определить значения параметров а и b [74].

ПРИМЕР II. Исследование зонной характеристики пропускания выполненного из стандартного цветного стекла абсорбционного светофильтра дало в пяти точках на базовом диаметра 40 мм следующие отклонения от номинального значения =80 %:

10

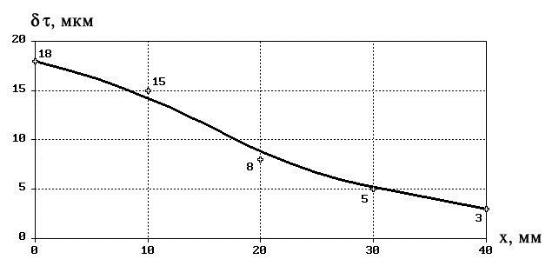
По этим данным построен график, представленный на рис. Е2.

Рис. E2. Отклонения пропускания в разных точках поперечника светофильтра.

Требуется установить закономерность отклонений от правильной цилиндрической формы светофильтра по толщине. При этом средняя квадратическая погрешность метода измерения про-

пускания σ =0,070=7 %.

Для решения этой задачи воспользуемся способом наименьших квадратов, с помощью которого найдем зависимость между x и δ , т.е. представим δ , как функцию x. Исходя из графика, приведенного на рис. E2 и памятуя закон Бугера, искомую функцию можно представить в виде экспоненты:

i a exp(b xi ),

где δ i - отклонение пропускания светофильтра от номинального значения 80% в i-й точке базового диаметра, xi - расстояние от края до i-й точки. Затем прологарифмируем это равенство:

ln i ln a b xi

и придем к линейной зависимости величины lnδ от x. Эту зависимость определяем, решая уже сугубо линейную задачу наименьших квадратов.

Для того, чтобы найти коэффициенты а и b, составим условные уравнения: