
functional_analysis
.pdf
1 Метрические пространства
Многие важные понятия и утверждения математического анализа, в частности, связанные с пределами и непрерывностью, опираются на понятие расстояния. Причем сами определения этих понятий, а также формулировки и доказательства соответствующих утверждений во многих случаях не зависят от конкретного способа задания расстояния. В них используются лишь основные свойства расстояния: неотрицательность, симметрия и неравенство треугольника. Формализация этих свойств расстояния приводит к понятию метрического пространства.
Пусть X произвольное множество.
Определение 1. Метрикой называется числовая функция X £ X ! ! R которая любой упорядоченной паре (x,y) элементов x, y 2 G ставит в соответствие однозначно определенное значение r(x,y) 2 R расстояние
îò x äî y, обладающая свойствами: а) r(x,y) = 0 , x = y,
á) r(x,y) = r(y,x) (аксиома симметрии),
â) r(x,z) 6 r(x,y) + r(y,z) (аксиома треугольника), ãäå x, y, z произвольные элементы X .
Множество, на котором задана некоторая метрика, называется метрическим пространством. Элементы метрического пространства называются точками.
Понятия метрического пространства введено в науку в начале XX столетия французским математиком М. Фреше. Приведем примеры метри- ческих пространств.
Пример 1. Множество действительных чисел с расстоянием r(x,y) = jx ¡yj
образует метрическое пространство.
Пример 2. n-мерное евклидово пространство Rn, элементами (точками) которого являются всевозможные упорядоченные совокупности из n
действительных чисел x = (x1,x2,:::,xn) è y = (y1,y2,:::,yn) с расстоянием
s
r(x,y) = |
n |
kå=1(xk ¡yk)2: |
1
Пример 3. Рассмотрим то же самое множество, упорядоченных
групп из |
n действительных чисел, но расстояние определим в нем |
|
формулой |
|
n |
|
|
|
|
r1 |
(x,y) = å jxk ¡ykj: |
|
|
k=1 |
Обозначим это метрическое пространство символом Rn.
1
Пример 4. Возьмем множество, что и в примерах 2 и 3, и определим расстояние между его элементами формулой
r1(x,y) = max jxk ¡ykj:
16k6n
Это пространство, которое мы обозначим Rn
1, во многих вопросах анализа не менее удобно, чем евклидово пространство Rn.
Последние три примера показывают, что на одном и том же множестве можно задавать разные метрики, в результате получаются разные метрические пространства. Отметим также, что, и наоборот, на разных множествах метрика может быть задана по одному и тому же правилу.
Пример 5. Пространство непрерывных функций. Множество всех непрерывных действительных функции, определенных на сегменте [a,b], с расстоянием
r( f ,g) = max jf (t) ¡g(t)j |
(1) |
a6t6b |
|
образует метрическое пространство.
Аксиомы а), б) метрики, очевидно, выполнены, а неравенство треугольника следует из того, что
jf (t) ¡g(t)j 6 jf (t) ¡h(t)j + jh(t) ¡g(t)j 6 r( f ,h) + r(h,g),
ò. å.
r( f ,g) = max jf (t) ¡g(t)j 6 r( f ,h) + r(h,g):
a6t6b
Это пространство играет очень важную роль в анализе. Мы будем его обозначать символом C[a,b].
Метрика (1), так называемая равномерная метрика в C[a,b], используется тогда, когда мы желаем заменить одну, функцию, другой, например полиномом, по которой можно было бы вычислять значения первой
функции с нужной точностью в любой точке t 2 [a,b]. Величина r( f ,g) как раз характеризует точность такого приближенного расчета.
2
Пример 6. Рассмотрим тоже множество функций, что и в предыдущем примере, но с интегральной метрикой:
r( f ,g) = Zb jf (t) ¡g(t)jdt:
a
Обозначим это метрическое пространство C1[a,b].
Пример 7. В множестве C(k)[a,b] функции, определенных на [a,b] и имеющих на этом отрезке непрерывные производные до порядка k вклю- чительно, можно определить следующую метрику:
|
|
|
|
|
|
r( f ,g) = maxfM0,:::,Mkg, |
|
|
|
|
(2) |
||||||||
ãäå |
|
|
|
Mi = amaxt b jf (i)(t) ¡g(i)(t)j, |
i = 0,1,:::,k: |
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
6 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, например, что функции задают координаты дви- |
||||||||||||||||||
жущейся точки в зависимости от времени. Если ставится огра- |
|||||||||||||||||||
ничение на допустимый район пребывания точки в промежуток |
|||||||||||||||||||
времени |
|
[a,b] |
и запрещается превышать определенную скорость, |
||||||||||||||||
à, |
кроме |
òîãî, |
желают иметь некоторый комфорт, состоящий в |
||||||||||||||||
том, что ускорения не должны |
превышать определенный уровень, |
||||||||||||||||||
òî, |
естественно |
рассмотреть |
|
äëÿ |
функций |
f ,g 2 C(2)[a,b] |
набор |
||||||||||||
характеристикамn |
два движения |
f , g считать близкими, еслиo |
величина (2) |
||||||||||||||||
amaxt b j |
|
|
¡ |
|
j a t b j |
f 0(t) |
¡ |
g0 |
j |
a t b j |
f 00(t) |
¡ |
g00 |
j |
è ïî |
ýòèì |
|||
|
6 6 |
f (t) |
|
g(t) , max |
|
|
(t) , max |
|
|
(t) |
|
|
|||||||
|
|
|
|
|
6 6 |
|
|
|
|
|
6 6 |
|
|
|
|
|
|
|
|
äëÿ íèõ ìàëà.
Пример 8. Укажем еще один пример метрического пространства. Его элементами являются всевозможные последовательности действи-
тельных чисел x = (x1,x2,:::,xn,:::), такие, что
å1
jxkjp < 1,
k=1
ãäå p > 1 некоторое фиксированное число, а расстояние определяется
формулой |
Ãk=1 jxk ¡ykjp! |
: |
r(x,y) = |
||
|
å1 |
1=p |
|
|
Это метрическое пространство обозначим lp.
3
2 Геометрия метрического пространства.
Мы введем здесь некоторые понятия теории метрических пространств. Эти понятия мы неоднократно используем в дальнейшем. Перенесем сначала из трехмерного евклидова пространства в произвольное метрическое пространство понятие шара.
Открытым шаром B(x0,r) в метрическом пространстве X мы будем называть совокупность точек x 2 X , удовлетворяющих условию
B(x0,r) = fx 2 X j r(x,x0) < rg:
Точка x0 называется центром этого шара, а число r его радиусом. Открытый шар радиуса e с центром x0 мы будем называть также e-окрестностью точки x0.
Замкнутым шаром B[x0,r] мы назовем совокупность точек x 2 X , óäî-
влетворяющих условию r(x,x0) 6 r:
 R1, т. е. на числовой прямой, открытый шар будет интервалом (x0 ¡
r,x0 |
+ r), а замкнутый отрезком [x0 ¡r,x0 |
+ r]. |
|
|
||||
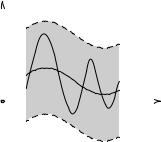
 C[a,b] øàð B( f0,r) состоит из всех функций f (t), удовлетворяющих |
||||||||
условию jf (t)¡ f0 |
(t)j < r на всем отрезке [a,b], т. е. графики которые уме- |
|||||||
щаются в полоске, показанной на рис. |
|
|
|
|||||
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0( |
|
|
|
||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
)+ |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
0( |
|
|
|
||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
a |
|
b |
t |
|
|
|
|
|
f |
|
|
|
|
|
|
|
0( |
|
|
|
||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
)¡r |
|
|
|
Множество точек метрического пространства называется ограниченным, если оно содержится в каком нибудь шаре.
3 Сходимость в метрическом пространстве
Наличие расстояния позволяет определить в метрическом пространстве понятие предела.
4

Пусть fxng последовательность точек в метрическом пространстве X . Говорят, что эта последовательность сходится к точке x èç X , åñëè
= 0:
nlim!1 r(x,xn)
Будем писать в этом случае xn ! x ïðè n ! 1 èëè lim = x.
n!1 xn
Теорема 1. Последовательность точек fxng метрического пространства не может иметь двух различных пределов.
Доказательство. Пусть xn ! x è xn ! y. По аксиоме треугольника r(x,y) 6 r(x,xn) + r(xn,y). Но правая часть стремится к нулю при n ! 1, а левая неотрицательна, следовательно, r(x,y) = 0 è x = y. 
Выясним смысл сходимости в C[a,b], fn ! f â C[a,b] означает, что
max jfn(t) ¡ f (t)j ! 0, т. е. сходимость равносильна равномерной сходи-
a6t6b
мости функций.
Сходимость в C1[a,b] накладывает менее тяжелые требования на функции. Например, если положить
fn(t) = ( |
1 |
ïðè |
1=n 6 t 6 1: |
|
nt |
ïðè |
0 6 t < 1=n, |
Тогда в метрике пространства C1[a,b], ïðè f (t) ´ 0,
|
|
|
|
|
|
|
1 |
|
|
|||
r( fn, f ) = Z0 jf (t) ¡ fn(t)jdt = Z0n (1 ¡nt)dt = |
||||||||||||
1 |
|
|
¶¯¯0 |
|
|
|
|
|
|
|||
|
= µt ¡ 2 |
= 2n ! : |
||||||||||
|
|
nt2 |
|
|
1 |
1 0 |
|
|
||||
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
В то же время fn(0) = 0 ïðè âñåõ n. |
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
fn(t) |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
O |
1 |
|
|
|
1 t |
|||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5

4 Полные метрические пространства
Представление о числовой оси как о множестве полном (на ней нет ¾дыр¿, она вся заполнена вещественными числами) выражается в математическом анализе удобнее всего с помощью известного критерия Коши. Эта же идея лежат в основе понятия полноты метрического пространства.
Начнем со следующего важного определения.
Определение 2. Последовательность fxng точек метрического пространства X мы будем называть фундаментальной, åñëè r(xn,xm) ! 0 ïðè n,m ! 0.
Теорема 2. Если последовательность fxng сходится к пределу x, то она фундаментальна.
Доказательство. Пусть xn ! x. Тогда
r(xn,xm) 6 r(xn,x) + r(x,xm) ¡¡¡¡¡¡!
m,n!0 0,
ò. å. fxng фундаментальна.
Определение 3. Метрическое пространство называется полным, если любая фундаментальная последовательность его точек имеет предел в этом пространстве.
Âпротивном случае метрическое пространство называется непол-
íûì.
Âобщем случае обратное утверждение является неверным. Например, если из множества R удалить, например, число 0, то в стандартной
метрике множество R n f0g уже не будет полным пространством. Дей-
ствительно, последовательность xn |
= 1 , n 2 N, его точек фундаментальна, |
но она не имеет предела в Rnf0g. |
n |
|
|
Пример 9. Покажем, что метрическое пространство C[0,1] является |
|
полным. |
|
Метрика в пространстве C[0,1] |
определяется как |
r( f ,g) = max jf (t) ¡g(t)j:
06t61
6
Рассмотрим произвольную фундаментальную последовательность ffn(t)g, r( fn, fm) ! 0 ïðè m,n ! 1. Это означает, что
8e 9N : 8m,n > N,8t 2 [0,1] ) jfm(t) ¡ fn(t)j < e:
Из этого следует, что при любом фиксированном t 2 [0,1] числовая последовательность ffn(t)g является фундаментальной, и поэтому имеет предел (с силу полноты R). Перейдя к пределу при m ! 1, получим, что
8e 9N : 8n > N,8t 2 [0,1] ) jfn(t) ¡ f (t)j 6 e,
ãäå f (t) некоторая функция. Это означает, что
r( fn, f ) ! 0:
Докажем, что f (t) непрерывная функция. Фиксируем точку t0 2 [0,1] и проверим непрерывность функции f в этой точке. Пусть t такое, что t 2 2 [0,1]. Тогда
jf (t) ¡ f (t0)j = jf (t) ¡ fn(t) + fn(t) ¡ fn(t0) + fn(t0) ¡ f (t0)j 6 jf (t) ¡ fn(t)j + jfn(t) ¡ fn(t0)j + jfn(t0) ¡ f (t0)j
берем такое n, ÷òî r( fn, f ) < e
<e + jfn(t) ¡ fn(t0)j + e:
Âсилу непрерывности fn 9d : jt ¡t0j < d ) jfn(t) ¡ fn(t0)j < e. Таким образом, получаем, что
8e 9d : jt ¡t0j < d ) jf (t) ¡ f (t0)j < 3e,
следовательно, f (t) непрерывно.
Рассмотрим еще пример неполного метрического пространства.
Пример 10. В множестве функций, определенных и непрерывных на отрезке [¡1,1], введем метрику по формуле
r( f ,g) = Z1 jf (t) ¡g(t)jdt:
¡1
7
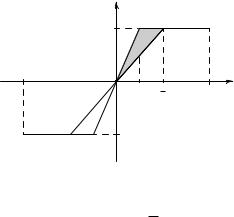
Покажем, что это метрическое пространство является неполным. |
||||
Рассмотрим последовательность функций |
||||
fn(t) = |
8¡nt |
ïðè |
|
1=n 6 t 6 1=n, |
|
1 |
ïðè |
¡1 6 t 6 1=n, |
|
|
< 1 |
ïðè |
¡ |
1=n 6 t 6 1, |
|
: |
|
|
|
1 |
|
|
|
|
¡1 |
1 |
1 |
1 |
t |
O |
||||
|
n |
m |
|
|
¡1 |
|
|
|
|
Очевидно, для любых n è m (n > m)
Z¡1 jfn(t) ¡ fm(t)jdt = m ¡ n ! |
|
|
1 |
|
|
1 |
1 |
0 |
и поэтому последовательность непрерывных функций фундаментальна относительно метрики.
Покажем, что в множестве непрерывных функций предела нет, ибо если бы непрерывная функция f 2 C[¡1,1] была пределом указанной
последовательности в смысле интегральной метрики, то на промежутке ¡1 6 t < 0 функция f должна была бы быть постоянной, равной ¡1, à
на промежутке 0 < t 6 1 постоянной, равной 1, что несовместимо с непрерывностью f в точке t = 0, если f некоторая функция C[¡1,1] è
½¡1 |
ïðè |
0 6 t 6 1: |
|
s(t) = |
1 |
ïðè |
¡1 6 t < 0, |
Òàê êàê |
nlim!1 Z¡1 jfn(t) ¡s(t)jdt = 0 |
|
|
|
1 |
и, в силу непрерывности f (t), |
|
|
Z¡1 jf (t) ¡s(t)jdt 6= 0, |
|
1 |
8
то, из неравенства |
|
|
Z¡1 jf (t) ¡s(t)jdt 6 Z¡1 jf (t) ¡ fn(t)jdx + Z¡1 jfn(t) ¡s(t)jdt, |
||
1 |
1 |
1 |
следует, что r( fn, f ) 6!0 ïðè n ! 1.
5 Непрерывные отображения метрических пространств.
Пусть (X ,r1) è (Y ,r2) два метрических пространства и f отображение пространства X â Y . Это отображение называется непрерывным в точке a 2 X , åñëè
8e > 0 9d > 0 : 8x 2 X : r1(x,a) < d ) r2( f (x), f (a)) < e:
Можно также дать определение непрерывности отображения, использую ¾язык последовательностей¿.
Отображение f : X ! Y называется непрерывным в точке a 2 X , если для любой последовательности fxng точек из X , сходящейся к a, последовательность точек ff (xn)g, сходится к f (a).
Если отображение f непрерывно во всех точках пространства X , то говорят, что f непрерывно на X .
6Принцип сжимающих отображений и его применения
Здесь будет установлен принцип, который, несмотря на всю свою простоту, оказывается средством эффективного доказательства многих теорем существования.
Пусть X метрическое пространство.
Определение 4 (сжимающиe отображение). Отображение A пространства X в себя называется сжимающим отображением если существует такое число a 2 (0,1), что для любых двух точек x,y 2 X
выполняется неравенство
r(Ax,Ay) 6 ar(x,y): |
(3) |
9

Всякое сжимающее отображение непрерывно. Действительно, если xn ! x, òî â ñèëó (3) è Axn ! Ax.
Точка x называется неподвижной точкой отображения A, åñëè Ax = x. Иначе говоря, неподвижные точки это решения уравнения Ax = x.
Теорема 3 (Принцип сжимающих отображений). Всякое сжимающее отображение, определенное в полном метрическом пространстве X , имеет одну и только одну неподвижную точку.
Доказательство. Пусть x0 произвольная точка в X . Положим x1 = Ax0, x2 = Ax1, :::, xn = Axn¡1, :::
Покажем, что последовательность fxng фундаментальная. Отображение A сжимающее, поэтому в силу (3)
r(x1,x2) = r(Ax0,Ax1) 6 ar(x0,x1),
r(x2,x3) = r(Ax1,Ax2) 6 ar(x1,x2) 6 a2r(x0,x1),
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
r(xn,xn+1) 6 anr(x0,x1),
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Далее, считая для определенности m > n,
r(xn,xm) = r(xn,xn+1) + r(xn+1,xn+2) + ::: + r(xm¡1,xm) 6
6(an + an+1 + ::: + am¡1)r(x0,x1) =
6an(1 + a + a2 + a3 + ::: + am¡n¡1)r(x0,x1) =
= an 1 |
¡am¡n |
an |
1 |
: |
|
1 ¡a r(x0,x1) |
|||||
|
1 ¡a r(x0,x1) 6 |
|
|
Ò. ê. a < 1, то при достаточно большом n эта величина сколь угодно мала. В силу полноты X последовательность fxng, будучи фундаментальной,
имеет предел. Положим
x = lim :
n!1 xn
Тогда в силу непрерывности отображения A
Ax = A lim |
= lim |
= lim |
+1 = x: |
n!1 xn |
n!1 Axn |
n!1 xn |
|
10
