Prak_alg

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

И.Н. Булгакова

ДИСКРЕТНАЯ МАТЕМАТИКА

ЭЛЕМЕНТЫ ТЕОРИИ, ЗАДАЧИ И УПРАЖНЕНИЯ

Часть 1

Учебное пособие для вузов

2-е издание, переработанное и дополненное

Издательско-полиграфический центр

Воронежского государственного университета

2008

1. ТЕОРИЯ МНОЖЕСТВ И ОТНОШЕНИЙ

1.1 Элементы теории множеств

Под множеством понимается совокупность некоторых объектов (элементов), объединенных некоторым признаком. Множества обычно обозначают большими буквами алфавита Α, Β , Χ ,Υ , Ζ , Ω . Элементы,

входящие в множество, обозначаются малыми буквами a,b, x, y, z,ω . За-

пись x Î Χ означает, что x является элементом множества Χ , а запись x Χ означает, что x не принадлежит множеству Χ . Два множества счи- таются равными, если они состоят из одних и тех же элементов.

Для описания множества пользуются двумя способами. Первый спо- соб состоит в простом перечислении его элементов. Так, запись Α = {0,1,5}

означает, что множество Α состоит из трех чисел 0,1 и 5. Второй способ со- стоит в определении множества с помощью некоторого свойства P, позво- ляющего определить, принадлежит ли данный элемент данному множеству или нет. В этом случае используется коллективизирующее обозначение

Α = {x : P(x)},

которое читается следующим образом: множество Α состоит из всех эле- ментов x , для которых P(x) истинно. Если свойство P относится к эле-

ментам некоторого множества Χ , то будем писать также Α = {x Χ : P(x)}. Например, множество {1,2,3,4,5} можно задать следую-

щим образом:

{1,2,3,4,5}= {x : x − целое число из интервала [1,5]}.

Множество, не содержащее элементов, называется пустым множест- вом и обозначается Æ .

Знаком обозначим отношение включения между множествами, т.е. Α Β , если каждый элемент множества Α есть элемент множества Β . Ес- ли Α Β , то говорят, что множество Α есть подмножество множества Β .

Равенство двух множеств Α и Β означает выполнение двух вклю- чений: Α Β и Β Α .

Если Α Β и Α ¹ Β , то говорят, что Α есть собственное подмно- жество Β и пишут Α Ì Β .

Множество всех подмножеств множества Α называется множест- вом-степенью и обозначается Ρ (Α).

Заметим, что: a) Χ Χ ; б) если Χ ÍΥ , Υ Í Ζ , то Χ Ζ ; в) ес- ли Χ ÍΥ , Υ Í Χ , то Χ =Υ .

Не надо смешивать отношения принадлежности и включения. Хотя 1 {}1 , {}1 {{}1 }, не верно, что 1 {{}1 }, так как единственным элементом

множества {{}1 } является {}1 .

Пустое множество есть подмножество любого множества.

3

Число элементов в множестве Χ обозначается Χ .

Рассмотрим методы получения новых множеств из уже существую-

щих.

Объединением множеств Α и Β называется множество Α È Β , все элементы которого являются элементами множества Α или Β :

Α È Β = {x : x Î Α или x Î Β}.

Пересечением множеств Α и Β называется множество Α Ç Β , эле- менты которого являются элементами и множества Α , и множества Β :

Α Ç Β = {x : x Î Α и x Î Β}.

Очевидно, что выполняются включения

Α Ç Β Í Α Í Α È Β и Α Ç Β Í Β Í Α È Β .

Разностью множеств Α и Β называется множество Α \ Β тех эле- ментов из Α , которые не принадлежат Β :

Α \ Β = {x : x Î Α и x Ï Β}.

Симметричной разностью множеств Α и Β называется множество

Α + Β = Α \ Β È Β \ Α .

Если все рассматриваемые в данный момент множества являются подмножествами некоторого множества U , то множество U называют универсальным для данного рассмотрения.

Дополнением множества Α называется множество

Α = U \ Α .

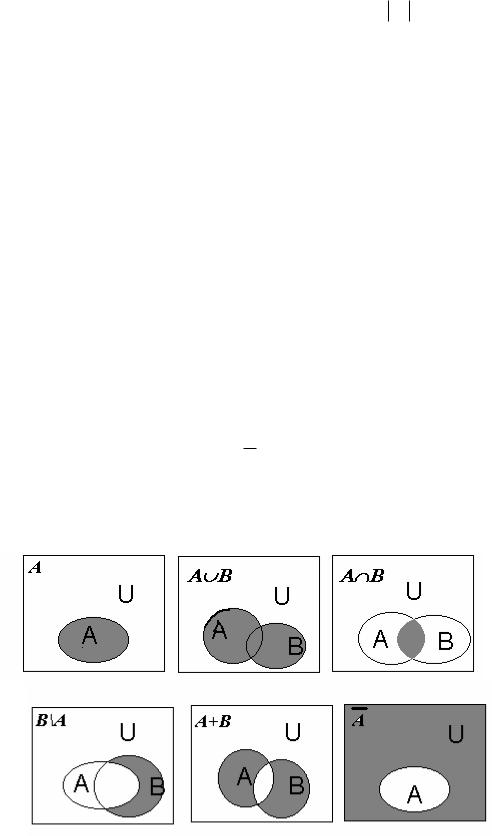
Для наглядного представления отношений между подмножествами какого- либо универсального множества используются диаграммы Эйлера – Венна.

Операции над множествами имеют следующие приоритеты в поряд- ке убывания: операция взятия дополнения, операция пересечения, опера- ция объединения.

4

Отметим следующие основные законы для операций над множествами:

1.Α È Β = Β È Α ( коммутативность объединения);

2.Α Ç Β = Β Ç Α (коммутативность пересечения);

3.Α È (Β È Μ )= (Α È Β )È Μ (ассоциативность объединения);

4.Α Ç (Β Ç Μ )= (Α Ç Β )Ç Μ (ассоциативность пересечения);

5.Α È (Β Ç Μ )= (Α È Β )Ç (Α È Μ )(1-й закон дистрибутивности);

6.Α Ç (Β È Μ )= (Α Ç Β )È (Α Ç Μ )(2-й закон дистрибутивности);

7.Α È Æ = Α ;

8.Α ÈU = U ;

9.Α Ç Æ = Æ ;

10.Α ÇU = Α ;

11.Α È Β = Α Ç Β ( закон де Моргана);

12.Α Ç Β = Α È Β ( закон де Моргана);

13.Α È (Α Ç Β )= Α (закон поглощения);

14.Α Ç (Α È Β )= Α (закон поглощения).

Рассмотрим методику решения задач по данной теме.

Пример 1. Равны ли следующие множества:

1){2,4,5} и {2,4,5,2};

2){1,2} и 1,2 ;

3){1,2,3} и {{}1 ,{2},{3}};

4){{1,2},3} и {{}1 ,{2,3}}.

Решение. Для доказательства равенства произвольных множеств нужно проверить, что первое множество включено во второе, а второе, в свою очередь, включено в первое, т.е. любой элемент первого множества является элементом второго множества, а любой элемент второго множе- ства является элементом первого множества.

Проверка дает положительный результат для множеств из пункта 1). Это можно наглядно показать на следующей схеме, где стрелочка, идущая от элемента, показывает, какой элемент в другом множестве ему соответствует.

Множества из пункта 2) неравны, так как, например, элемент 1 из первого множества не имеет себе равного во втором множестве. Второе множество состоит из единственного элемента – множества {1,2}.

5

Множества, указанные в пункте 3), неравны, так как элементами первого множества являются числа 1, 2, 3 , а элементами второго множества являются множества, состоящие из одного элемента {}1 ,{2},{3}.

Пункт 4) сделайте самостоятельно.

Пример 2. Следующие множества заданы перечислением своих эле- ментов, задайте эти множества с помощью характерного для их элементов свойства.

1) Α = {2,4,6,8,...,32};

Решение. Множество Α представляет собой множество четных на- туральных чисел от 1 до 32, поэтому это множество можно записать в виде

Α = {x Ν : x = 2n, n = 1,...,16}.

Множество Κ представляет собой множество столиц республик бывшего СССР, т.е. это множество можно записать в виде

Κ = {x : x − столица республики СССР}.

Пример 3. Приведите примеры таких множеств Α,Β ,Κ , для которых

Решение. В качестве примера множеств, удовлетворяющих условию из пункта 1), можно рассмотреть следующие множества

Α = {1,2} , Β = {{1,2} ,1} , Κ = {3,{{1,2} ,1}} .

Пункту 3) удовлетворяют множества

Α = {2,3}, Β = {{}1 ,{2,3}}, Κ = {2,3,4}.

Пункты 2) и 4) рассмотрите самостоятельно.

Пример 4. Докажите следующие тождества:

1)Α \ Β = Α Ç Β ; 2)Α È (Β \ Κ ) = (Α È Β )Ç (Α È Κ );

3)(Α È Β )Ç (Β È Α)= Α ; 4)Β Ç (Α \ Β ) = Æ ; 5)Α Ç (Β + Κ ) = (Α Ç Β )+ (Α Ç Κ ).

Решение. Для доказательства равенства 1) докажем два включения:

Α\ Β Í Α Ç Β ,

ΑÇ Β Í Α \ Β .

Доказательство первого включения проведем по схеме

6

а доказательство второго включения по схеме

Заметим, что в данном примере мы могли рассмотреть не две схемы, а одну, но вместо знака следствия использовать знак равносильности .

Тождество 2 можно также доказать с помощью двух включений, но можно и не использовать данную схему, а опираться на уже доказанное тождество 1) и на основные законы 1–14. Мы приведем данный способ до- казательства, причем вверху над равенствами будем писать либо 1) – это означает, что используется тождество 1), либо номер используемого ос- новного закона. Итак,

Α È (Β \ Κ ) =1) Α È (Β Ç Κ )=5) (Α È Β )Ç (Α È Κ ).

Аналогично можно доказать равенства 3), 4), 5). Для равенства 4) приведем еще один способ доказательства – доказательство от против- ного. Предположим противное, что множество Β Ç (Α / Β ) не пусто, т. е.

существует хотя бы один элемент

Никакой элемент x не может одновременно принадлежать и самому множеству, и его дополнению, поэтому мы пришли к противоречию.

Пример 5. Пусть Α, Β, Κ – такие множества, что Β Α Κ . Най- дите множество Χ , удовлетворяющее системе уравнений

следует, что Α Ç Χ ′ = Æ .

Итак, нам осталось найти множество Χ ′ . Заменим Χ во втором урав- нении на Χ = Β È Χ ′. Получим Α È (Β È Χ ′) = Κ . По ассоциативному за- кону (Α È Β )È Χ ′ = Κ . Из включения Β Α следует, что Α Β = Α , по- этому получаем равносильное уравнение Α È Χ ′ = Κ . Два факта Α Ç Χ ′ = Æ и Α Κ позволяют заключить, что решением последнего урав- нения является множество Χ ′ = Κ \ Α . Окончательно

7

Χ = Β È (K \ Α).

Пример 6. Докажите, что условие Α Β равносильно каждому из следующих условий:

1) Α Ç Β = Α ; 2) Α È Β = Β .

Решение. Докажем, что Α Β равносильно условию 1).

Итак, пусть Α Β , докажем равенство Α Ç Β = Α . Равенство будем доказывать в два включения. Пусть

x Î Α Ç Β Þ x Î Α .

Обратно, пусть

x Î Α ÞΑÍΒ x Î Α, x Î Β Þ x Î Α Ç Β .

Теперь предположим, что выполнено условие 1), докажем, что Α Β . Рассмотрим

x Î Α ÞΑÇΒ =Α x Î Α Ç Β Þ x Î Β .

Равносильность условия Α Β условию 1) мы доказали, равносиль- ность условию 2) докажите самостоятельно.

Пример 7. Докажите для произвольных множеств Α, Β, Κ :

кой, что x′Î Α È Κ , x′Ï Β È Κ . Нам известно, что Α Β , поэтому суще-

ствует некоторый элемент x* Î Α и x* Ï Β . В силу условия Α Ç Κ = Æ , данный элемент x* Ï Κ . Таким образом, x* Î Α È Κ , x* Ï Β È Κ .

2) Нам нужно доказать, что существует хотя бы один элемент в мно-

x* Ï Β . Итак, мы построили элемент x* Î Α и x* Ï Β .

Пример 8. Докажите, что для произвольных множеств Α, Β спра- ведливо равенство Ρ (Α Ç Β ) = Ρ (Α)Ç Ρ (Β ).

Решение. Доказательство проведем в виде двух включений, объеди- нив их одной записью. Пусть

Χ Î Ρ (Α Ç Β ) Û Χ Í Α Ç Β Û Χ Í Α, Χ Í Β Û Û Χ Î Ρ (Α), Χ Î Ρ (Β ) Û Χ Î Ρ (Α)Ç Ρ (Β ).

8

ЗАДАЧИ И УПРАЖНЕНИЯ

1. Каждое из следующих множеств задайте в виде некоторого интервала числовой прямой:

1){x Î R : $y Î R x2 + y2 = 1};

3){a Î R : $x Î R 3x2 + 2ax + a < 0} .

2.Вставьте между множествами символ или так, чтобы получилось истинное утверждение.

3.Перечислите элементы каждого из следующих множеств:

1){x : x Í {}1 };

2){x : x Í {1,2,3}};

3){x : x Í Æ}.

4.Докажите следующие тождества:

1)(Α \ Β )È (Α Ç Β ) = Α;

2)Α Ç Β = Α Ç (Α È Β );

3)(Α È Β )\ (Α Ç Β ) = Α + Β;

4)(Α \ Β )È (Α \ Β )= (Α È Β )\ (Α Ç Β );

5)(Α \ Β )È (Α \ Β )= (Β È Α)Ç (Α È Β );

6)Α \ (Α \ Β ) = Α Ç Β;

7)Β È (Α \ Β ) = Α È Β;

8)(Α + Β )+ Κ = Α + (Β + Κ );

9)Α + Α = Æ .

5.Считая Λ универсальным множеством для данного рассмотрения, най-

дите множество Х, удовлетворяющее следующим условиям: 1)Α \ Χ = Α, Α È Χ = Λ;

2)Α Ç Χ = Æ, Α È Χ = Λ; 3)Α \ (Α \ Χ ) = Æ; 4)Α \ Χ = Æ, Α È Χ = Α;

5)Α \ (Α \ Χ ) = Æ, Α Ç Χ = Æ .

9

7.Каждое из следующих утверждений либо докажите, либо покажите при помощи диаграмм Эйлера – Венна, что оно не всегда верно:

1)(Α È Β )Ç Κ = Α È (Β Ç Κ );

2)(Α \ Β )È Β = Α;

3)(Α È Β )\ Β = Α;

4)(Α Ç Β )\ Α = Æ;

5)(Α \ Β )È Κ = (Α È Κ )\ (Β È Κ );

6)(Α Ç Β )È (Β Ç Α)Í Β;

7)Β = (Α Ç Β )È (Β Ç Α)Þ Α = Æ .

8.Верно ли, что:

1)Α È Β = Α È Κ Þ Β = Κ ;

2)Α Ç Β = Α Ç Κ Þ Β = Κ ;

3)Α È Β = Α È Κ и Α Ç Β = Α Ç Κ Þ Β = Κ .

9.Докажите:

1.(Α È Β )Ç Κ = Α È (Β Ç Κ ) Û Α Í Κ ;

2.Α = Β Û Α + Β = Æ;

3.Α È Β = Æ Û Α = Β = Æ;

4.(Α È Β )\ Β = Α Û Α Ç Β = Æ;

5.Α \ Β = Α Û Β \ Α = Β;

6.Α È Β = Α \ Β Û Β = Æ;

7.Α \ Β = Α Ç Β Û Α = Æ;

8.Α È Β Í Κ Û Α Í Κ и Β Í Κ ;

9.Α Í Β È Κ Û Α \ Β Í Κ ;

10.Κ Í Α Ç Β Û Κ Í Α и Κ Í Β ;

11.Α Ç Β = Α È Β Û Α = Β ;

12.Α Í Β Í Κ Û Α È Β = Β Ç Κ ;

13.Α Í Β Þ Α \ Κ Í Β \ Κ ;

14.Β Í Α и Κ = Α \ Β Þ Α = Β È Κ ;

15.Α È Β = Α Þ Α Ç Β = Β .

10.Объединением семейства множеств Αi (i Ι ) называется множество

UΑi = {x : $j ÎΙ x Î Α j }.

iΙ

10