Prak_alg

Пересечением семейства множеств Αi (i Î Ι ) называется множество

1) последовательности непустых множеств Χ 1, Χ 2 ,..., Χ n ,..., такой,

что Χ 1 É Χ 2 É ... и IΧ n = ;

nΝ

2) последовательности множеств, отличных от универсального мно-

жества Λ , такой, что Χ 1 Ì Χ 2 Ì ...и UΧ n = Λ ;

nΝ

3) семейства множеств такого, что пересечение любого конечного числа множеств из этого семейства непусто, а пересечение всех множеств пусто.

1.2 Прямое произведение множеств. Бинарные отношения

Произведением (или декартовым произведением) Χ 1 ´ Χ 2 двух не-

картовой системы координат. Данное понятие можно обобщить и на слу- чай n множеств. Если Χ 1 , Χ 2 ,..., Χ n – n непустых множеств, то их произ-

ведение состоит из всевозможных упорядоченных наборов (x1 , x2 ,..., xn ),

ется Χ n . Так, символом Rn обозначается множество упорядоченных век- торов n вещественных чисел.

Любое подмножество из произведения Χ ×Υ называется бинарным отношением. Если Χ =Υ , то бинарное отношение называется бинарным отношением на множестве Χ . Бинарные отношения обозначаются буква- ми φ, ρ, f ,... Если пара (x, y) принадлежит бинарному отношению ρ , то

пишут (x, y)Î ρ или x ρ y .

Для задания бинарного отношения ρ используют те же методы, что

и для произвольных множеств, кроме того, бинарное отношение, заданное на конечном множестве Χ , можно задать в виде графа, а бинарное отно- шение на множестве R можно задать в виде декартовой диаграммы. Под

11

графом бинарного отношения мы понимаем схему, в которой элементы множества Χ изображаются точками на плоскости, элементы x, y Χ ,

такие, что пара (x, y) ρ соединяются стрелкой, направленной от x к y , пары (x, x) ρ изображаются петлей вокруг точки x . Под декартовой диа- граммой понимают изображение пар (x, y) ρ в декартовой прямоуголь-

ной системе координат.

Областью определения бинарного отношения ρ называется множество

Dρ = {x Χ : y (x, y) ρ}.

Областью значений бинарного отношения ρ называется множество

Rρ = {y Υ : x (x, y) ρ}.

Бинарное отношение ρ на множестве Χ называется рефлексивным, если для любого x Χ пара (x, x) ρ . Если Χ – конечное множество, то рефлексивность бинарного отношения ρ означает, что на графе данного

бинарного отношения вокруг каждой точки x из Χ есть петля. Если Χ = R , то рефлексивность бинарного отношения ρ с точки зрения декар-

товой диаграммы означает, что в число изображенных точек войдут все точки прямой y(x) = x.

Бинарное отношение ρ на множестве Χ называется симметричным, если для любых x, y Χ из принадлежности пары (x, y) отношению ρ следует принадлежность этому отношению также пары (y, x). Если Χ – конечное множество, то симметричность бинарного отношения ρ означа-

ет, что на графе данного бинарного отношения все присутствующие стрел- ки двусторонние. Если Χ = R , то симметричность бинарного отношения

ρ с точки зрения декартовой диаграммы означает, что изображенное мно- жество симметрично относительно прямой y(x) = x.

Бинарное отношение ρ на множестве Χ называется антисиммет- ричным, если для любых x, y Χ из принадлежности пар (x, y) и (y, x) от- ношению ρ следует x = y . Если Χ – конечное множество, то антисим- метричность бинарного отношения ρ означает, что на графе данного би-

нарного отношения все присутствующие стрелки односторонние. Бинарное отношение ρ на множестве Χ называется транзитивным,

если для любых x, y, z Χ из принадлежности пар (x, y) и (y, z) отноше- нию ρ следует принадлежность этому отношению также пары (x, z).

Обратным отношением для ρ называется отношение

ρ −1 = {(x, y): (y, x) ρ}.

Композицией отношений ρ1 и ρ2 называется отношение

ρ2 o ρ1 = {(x, y): z (x, z) ρ1 , (z, y) ρ2 }.

12

Для любых бинарных отношений выполняются следующие свойства:

1.(ρ −1 )−1 = ρ ;

2.(ρ2 o ρ1 )−1 = ρ1−1 o ρ2−1 .

Пример 1. Перечислите элементы множеств Α × Β , Β × Α :

1)Α = {1,2}, Β = {3,4,5};

2)Α = , Β = {1,2,3,4}.

Решение. По определению

Α × Β = {(a,b): a Α, b Β}.

Порядок построения данного множества будет следующий: вначале перечислим все пары, первый элемент которых равен первому элементу множества Α , а второй элемент берется из множества Β в том порядке, в котором они записаны в множестве Β , затем аналогично берем второй элемент из Α и составляем пары со всеми элементами из Β и т.д.

Аналогичен и метод построения множества

Β × Α = {(b,a): b Β , a Α}.

ì(3,3,3,3),(3,3,3,4),(3,3,4,3),(3,3,4,4), ü

=ïï(3,4,3,3),(3,4,3,4),(3,4,4,3),(3,4,4,4),ïï . íï(4,3,3,3),(4,3,3,4),(4,3,4,3),(4,3,4,4),ýï ïî(4,4,3,3),(4,4,3,4),(4,4,4,3),(4,4,4,4)ïþ

Пример 3. Пусть на плоскости задана декартова система координат. Изобразите на плоскости следующее множество: Μ = [a,b]×[c,d],

где a,b,c,d R a < b, c < d .

Решение. При построении прямого произведения Μ = [a,b]×[c,d] каждой точке x из отрезка [a,b] ставятся пары (x, y), y [c,d], поэтому в

результате получим множество

13

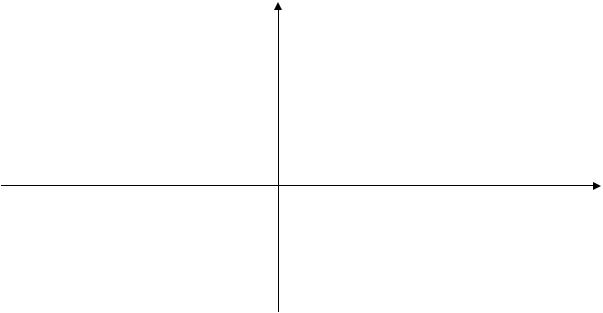
y

Пример 4. Докажите следующее равенство:

(Α Ç Β )´ (Κ Ç Μ ) = (Α ´ Κ )Ç (Β ´ Μ ).

Решение. Равенство двух множеств мы докажем с помощью двух включений, объединив их одной записью. Заметим, что элементами мно- жеств в данном случае являются упорядоченные пары точек. Итак, пусть

(x, y)Î (Α Ç Β )´ (Κ Ç Μ ) Û x Î (Α Ç Β ), y Î (Κ Ç Μ ) Û

Ûx Î Α, x Î Β , y Î Κ , y Î Μ Û x Î Α, y Î Κ , x Î Β , y Î Μ Û

Û(x, y)Î Α ´ Κ , (x, y)Î Β ´ Μ Û (x, y)Î (Α ´ Κ )Ç (Β ´ Μ ).

Пример 5. Докажите, что для любых непустых множеств Α,Β ,Κ из равенства (Α ´ Β )È (Β ´ Α) = Κ ´ Κ следует, что Α = Β = Κ .

Решение. Для доказательства данного утверждения установим два равенства Α = Κ и Β = Κ .

Для произвольных x Î Α и y Î Β

(x, y)Î Α ´ Β Þ (x, y)Î Κ ´ Κ Þ x Î Κ , y Î Κ Þ Α Í Κ , Β Í Κ .

бинарного отношения.

Решение. Расположим на плоскости точки множества Α . Точки x, y Î Α , для которых пара (x, y)Î ρ , соединим стрелкой, направленной от

14

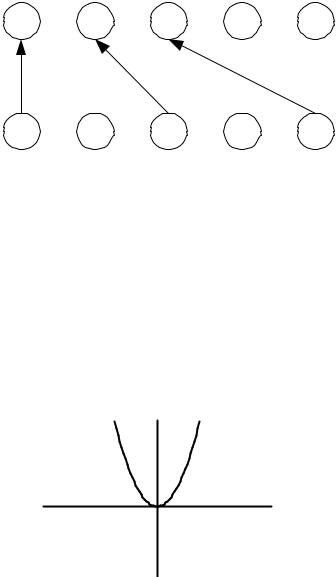
x к y . Пары (x, x) ρ изобразим петлей вокруг точки x . Результатом та-

кого построения будет граф

5 6 7 8 9

Пример 7. Для следующего бинарного отношения, определенного на множестве R , найдите область определения, область значений и нарисуйте

декартову диаграмму

ρ = {(x, y): x2 = y}.

Решение. В соответствии с определением

Dρ = {x R : y (x, y) ρ}= R .

Rρ = {y Υ : x (x, y) ρ} = R+ 0.

Декартова диаграмма для данного бинарного отношения имеет вид

y

x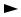

Пример 8. Для каждого из следующих бинарных отношений выясни- те, какими свойствами (рефлексивность, симметричность, антисимметрич- ность, транзитивность) оно обладает и какими не обладает.

1)ρ = {(1,2),(2,1),(1,1),(1,3),(3,2),(3,3)} на множестве Χ = {1,2,3};

2)ρ = {(x, y): x − y Ζ } на множестве Χ = R ;

3)ρ = {(x, y): 2x = 3y} на множестве Χ = Ζ ;

4)ρ = {(x, y): x y} на множестве Χ = Ρ (Ζ ).

Решение.

1) Данное отношение не является рефлексивным, поскольку для точ- ки 2 Χ пара (2,2) ρ ; не является симметричным, поскольку, например,

15

пара (1,3) ρ , а пара (3,1) ρ ; не является антисимметричным, поскольку, например, пары (1,2) и (2,1) принадлежат ρ , но 1 ¹ 2 ; не является транзи- тивным, поскольку, например (3,2) ρ, (2,1) ρ , а (3,1) ρ .

2) Данное отношение является рефлексивным, поскольку для любой точки x Î R разность x - x = 0 Î Ζ , т.е. (x, x)Î R ; является симметричным, поскольку принадлежность любой пары (x, y) отношению ρ означает x - y = k Î Ζ , но тогда y - x = -k Î Ζ , т.е. пара (y, x) ρ ; не является ан- тисиммеричным, поскольку, например, пары (1.2,3.2) ρ и (3.2,1.2) ρ , но 3.2 ¹ 1.2; является транзитивным, поскольку для любых x, y, z Î R принад- лежность пар (x, y) и (y, z) отношению ρ означает x - y = k Î Ζ и y - z = n Î Ζ , но тогда x - z = k + n Î Ζ , т.е. (x, z) ρ .

Æ Î Ρ (Ζ ) пересечение Æ Ç Æ = Æ , т.е. ( , ) ρ ; является симметрич- ным, поскольку принадлежность любой пары (x, y) отношению ρ означа- ет x Ç y ¹ Æ , но тогда y Ç x ¹ Æ , т.е. пара (y, x) ρ ; не является транзи- тивным, поскольку, например, пара ({1,2},{2,3}) ρ ({1,2}Ç{2,3}= {2}¹ Æ )

и пара ({2,3},{3,6,7}) ρ ({2,3}Ç{3,6,7}= {3}¹ Æ ), но пара ({1,2},{3,6,7}) ρ ,

так как {1,2}Ç{3,6,7}= Æ .

Пример 9. Пусть на множестве R заданы следующие бинарные от- ношения:

ρ1 = {(x, y): x = y2 }; ρ2 = {(x, y): x + y ≤ 2}; ρ3 = {(x, y) : x + y Ζ}.

Найдите обратные к данным бинарным отношениям и всевозможные композиции этих бинарных отношений.

Решение. Вначале выпишем обратные отношения:

ρ1−1 = {(x, y): (y, x) ρ1}= {(x, y): y = x2 };

ρ2−1 = {(x, y): (y, x) ρ2 }= {(x, y): y + x ≤ 2}= ρ2 ;

ρ3−1 = {(x, y): (y, x) ρ3}= {(x, y): y + x Ζ }= ρ3 .

16

В качестве примера рассмотрим некоторые композиции рассматри- ваемых бинарных отношений:

ρ1 o ρ2 = {(x, y): z (x, z) ρ2 , (z, y) ρ1}=

= {(x, y): $z x + z £ 2, z = y2 }= {(x, y): x + y2 £ 2} ;

={(x, y): x ³ 0, - x + y £ 2};

ρ2 o ρ3 = {(x, y): z (x, z) ρ3 , (z, y) ρ2 }=

={(x, y): z x + z Ζ , z + y ≤ 2}=

= {(x, y): z x + z = k Ζ , z + y ≤ 2}= {(x, y): k Ζ k − x + y ≤ 2}= R × R

ρ3 o ρ2 = {(x, y): z (x, z) ρ2 , (z, y) ρ3}=

={(x, y): z x + z ≤ 2, z + y Ζ }= R × R .

Остальные композиции постройте самостоятельно.

Пример 10. Пусть Χ – произвольное множество, обозначим симво- лом Ι Χ отношение на множестве Χ вида

Ι Χ = {(x, y): x = y}= {(x, x): x Χ }.

Докажите, что для любого бинарного отношения ρ между элемен-

тами множеств Α и Β выполняются равенства:

Ι Β o ρ = ρ, ρ o Ι Α = ρ .

Решение. Ι Β o ρ = {(x, y) Α × Β : z Β (x, z) ρ, (z, y) Ι Β }=

={(x, y) Α × Β : z Β (x, z) ρ, z = y}= {(x, y) Α × Β : (x, y) ρ}= ρ;

ρoΙ Α = {(x, y) Α × Β : z Α (x, z) Ι Α , (z, y) ρ}=

={(x, y) Α × Β : z Α x = z, (z, y) ρ}= {(x, y) Α × Β : (x, y) ρ}= ρ.

Пример 11. Пусть ϕ,φ, χ бинарные отношения, определенные на

множестве Χ . Докажите следующие утверждения:

1) если ϕ,φ – симметричные (антисимметричные) отношения, то

(ϕ Çφ )−1 – симметричное (антисимметричное) отношение; 2)(ϕ \ φ )o χ (ϕ o χ )\ (φ o χ ).

Решение. 1. Пусть ϕ,φ – симметричные отношения, докажем, что (ϕ Çφ )−1 – симметричное отношение. Пусть

(x, y)Î(ϕ Çφ )−1 Þ (y, x)Îϕ Çφ Þ ì(y, x)ϕ Þ

íî(y, x)Îφ

17

Пусть ϕ,φ – антисимметричные отношения, докажем, что (ϕ Çφ )−1 – антисимметричное отношение. Пусть

Þантисимметричность ϕ,φ x = y .

1.Докажем требуемое включение. Пусть

Þ (x, y)Î (ϕ \ φ )o χ

ЗАДАЧИ И УПРАЖНЕНИЯ

1. Пусть Χ = { ,×}. Перечислите все элементы множеств Χ3 , Χ4 .

2. Найдите геометрическую интерпретацию множества A ´ B , где A – множество точек отрезка [0,1], а Β – множество точек квадрата с вер-

шинами в точках (0,0), (0,1), (1,0), (1,1).

3.Доказать, что (Α × Β ) (Κ × Μ ) (Α Κ )× (Β Μ ) . При каких Α,Β ,Κ ,Μ включение можно заменить равенством.

4.Доказать, что для произвольных множеств Α,Β ,Κ :

1)(Α Β )× Κ = (Α × Κ ) (Β × Κ );

2)(Α \ Β )´ Κ = (Α ´ Κ )\ (Β ´ Κ );

3)Α × (Β \ Κ ) = (Α × Β )\ (Α × Κ ).

5. Пусть A ¹ Æ, B ¹ Æ и (Α × Β ) (Β × Α) = Κ × Μ . Доказать, что в

этом случае Α = Β = Κ = Μ .

6. Перечислите все элементы бинарного отношения ρ и нарисуйте его граф:

1)ρ = {(x, y): x < y} на множестве Χ = {1,2,3,4,5};

2)ρ = {(x, y): y = x +1}на множестве Χ = {1,2,3,4,5,6,7,8,9,10}.

18

7. Для каждого из следующих бинарных отношений, определенных на множестве R , найдите область определения, область значений и нари- суйте декартову диаграмму:

1)ρ = {(x, y): x ≤ y};

2)ρ = {(x, y): x = y};

3)ρ = {(x, y): x2 + 4y2 £ 1};

4)ρ = {(x, y): x2 = y2 };

5)ρ = {(x, y): y = log2 x};

6)ρ = {(x, y): y = sin x}.

8.Даны бинарные отношения ρ между элементами множеств Α и

Β, найдите область определения и область значений для данных бинарных отношений:

1) Α = {1,2,3,4,5},Β = {{}1 ,{1,2},{2,5},{3}}, ρ = {(x, y) Α × Β : x y};

9. Для каждого из следующих бинарных отношений выясните, каки- ми свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает и какими не обладает:

1)ρ = {(x, y)Î R ´ R : x2 = y2 };

2)ρ = {(x, y)Î R ´ R : x2 + y2 = 1};

3)ρ = {(x, y)Î R ´ R : x × y > 1};

4)ρ = {(x, y)Î R ´ R : y = x};

5)ρ = {(x, y)Î R ´ R : x + x2 = y + y2 };

6)ρ = {(x, y)Î Ζ ´ Ζ : x £ y +1};

7)ρ = {(x, y)Î Ζ ´ Ζ : 3 делится на x + y};

8)ρ = {(x, y)Î Ρ (Ζ ) ´ Ρ (Ζ ) : x Í y};

9)ρ = {(x, y)Î Ρ (Ζ ) ´ Ρ (Ζ ) : x Ç y = Æ}.

10. Пусть

1) ρ1 = {(x, y)Î R ´ R : x = y2 }; ρ2 = {(x, y)Î R ´ R : x + y £ 5}; 2) ρ3 = {(x, y)Î R ´ R : x3 = y}; ρ4 = {(x, y)Î R ´ R : y = sin x}.

11. Найдите всевозможные композиции ρi o ρk i,k = 1,2,3,4.

19

12. Покажите, что равенство ϕ oφ = φ oϕ верно не для любых бинар- ных отношений.

13.Докажите, что для любого бинарного отношения ρ выполняются условия: Dρ −1 = Rρ и Rρ −1 = Dρ .

14.Пусть ϕ,φ, χ – бинарные отношения, определенные на некото-

ром множестве. Докажите следующие утверждения:

1)(ϕ \ φ )−1 = ϕ −1 \ φ −1;

2)(ϕ Çφ )o χ Í (ϕ o χ )Ç (φ o χ );

3)(ϕ oφ )−1 = φ −1 oϕ −1 ;

4)(ϕ φ )−1 = ϕ −1 φ −1 ;

5)(ϕ Èφ )o χ = (ϕ o χ )È (φ o χ ).

15. Приведите примеры бинарных отношений:

1) рефлексивных и транзитивных, но не антисимметричных;

2) транзитивных и симметричных, но не рефлексивных;

3) рефлексивных и симметричных, но не транзитивных;

4) рефлексивных и транзитивных, но не симметричных.

16. Докажите, что если ρ – транзитивное и симметричное бинарное

отношение на множестве Α , область определения которого совпадает с Α , то ρ рефлексивно.

1.3 Специальные бинарные отношения

Рефлексивное, симметричное и транзитивное отношение ρ на мно-

жестве Χ называется отношением эквивалентности на множестве Χ . Для отношения эквивалентности вместо записи (x, y)Î ρ часто используют за-

пись x ≈ y (читается: x эквивалентен y ).

Классом эквивалентности, порожденным элементом x , называется подмножество множества Χ , состоящее из тех элементов y Χ , для ко-

торых (x, y)Î ρ . Класс эквивалентности, порожденный элементом x , обо- значается через [x]:

[x]= {y Î Χ : (x, y)Î ρ}.

Разбиением множества Χ называется совокупность попарно непере- секающихся подмножеств Χ таких, что каждый элемент множества Χ принадлежит одному и только одному из этих подмножеств. Всякое раз- биение множества Χ определяет на Χ отношение эквивалентности ρ :

(x, y)Î ρ тогда и только тогда, когда x и y принадлежат одному подмно- жеству разбиения. С другой стороны, всякое отношение эквивалентности

20