Методичка по ФОКИ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Ю. К. Тимошенко

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ КВАНТОВЫХ ЭЛЕКТРОННЫХ СОСТОЯНИЙ

Учебное пособие для ВУЗов ЧЕРНОВИК

Издательско – полиграфический центр Воронежского государственного университета 2014

Утверждено научно-методическим советом факультета прикладной математики, информатики и механики XX xxxxxx 2014 г., протокол № x

Рецензент: д – р физ. – мат. наук С. Д. Кургалин

Учебно-методическое пособие подготовлено на кафедре математического и прикладного анализа факультета прикладной математики, информатики и механики Воронежского государственного университета.

Рекомендуется для магистрантов кафедры математического и прикладного анализа.

Для специальности: 010500 – Прикладная математика и информатика

2

Содержание

1.1Одномерная квантовая яма . . . . . . . . . . . . . . . . . . 5

1.1.1Общие свойства решений одномерного стационарного уравнения Шрёдингера . . . . . . . . . . . . . 5

1.1.2Алгоритм . . . . . . . . . . . . . . . . . . . . . . . . 10

1.1.3Компьютерная программа . . . . . . . . . . . . . . . 13

1.1.4Условия задач. . . . . . . . . . . . . . . . . . . . . . 18

1.2Сферически симметричная квантовая яма . . . . . . . . . . 21

1.3Компьютерная программа . . . . . . . . . . . . . . . . . . . 26

1.3.1Условия задач. . . . . . . . . . . . . . . . . . . . . . 28

3

Введение

Актуальность темы

В последние годы во всем мире уделяется большое внимание исследованию физических свойств наноразмерных систем, (в частности, их пространственной и электронной структуры) в связи с необходимостью создания устройств с новыми свойствами самого различного назначения как в интересах фундаментальной науки, так и для технических приложений. ha| |bi

4

1.Численное моделирование стационарных состояний частицы квантовой яме

1.1. Одномерная квантовая яма

Основные литературные источники по данной теме: [1–3].

1.1.1.Общие свойства решений одномерного стационарного уравнения Шрёдингера

с математической точки зрения представляет собой задачу определения собственных значений E и собственных функций ψ(x) оператора

ном поле (называемом также потенциалом) U(x) , оператор Гамильтона

а ~ - постоянная Планка. Уравнение (2) называют одномерным стационарным уравнением Шрёдингера. Собственное значение оператора Гамильтона имеет смысл энергии соответствующей изолированной квантовой системы. Собственные функции называются волновыми функциями. Они полностью определяют квантовые состояния системы. Волновая функция однозначна и непрерывна во всем пространстве. Непрерывность волновой функции и её 1-ой производной сохраняется и при обращении U(x) в ∞ в некоторой области пространства. В такую область частица вообще не может проникнуть, то есть в этой области, а также на её границе (что следует из непрерывности волновой функции), ψ(x) = 0.

5

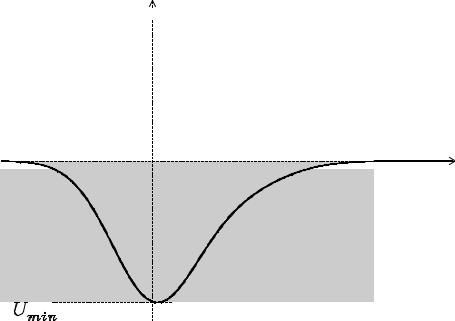
U(X)

Рис. 1. Потенциальное поле U(x) .

Оценим нижнюю границу энергетического спектра. Пусть минимальное значение потенциальной функции равно Umin . Очевидно, что hT i ≥ 0 и hUi > Umin . Потому, из уравнения (1) следует, что

Потенциал такого типа (называемый также потенциальной ямой) изображен на рис. (1). Для данной U(x) свойства решений уравнения Шредингера зависят от знака собственного значения E . Рассмотрим два случая.

1) E < 0 . Частица с отрицательной энергией совершает финитное движение. Оператор Гамильтона имеет дискретный спектр, то есть собственные значения и соответствующие собственные функции можно снабдить номерами (называемые квантовыми числами). При E < 0

6

Квантовые состояния дискретного спектра называют связанными состояниями. Частица, находящаяся в связанном состоянии, не способна уйти на бесконечность. То есть, плотность вероятности |ψk(x)|2 → 0 при x → ±∞ , но на всех конечных расстояниях =6 0 . В силу линейности стационарного уравнения Шрёдингера, волновые функции математически определены с точностью до постоянного множителя. Однако, из физических соображений, волновые функции должны быть нормированы следующим образом

+∞

−∞

Можно показать, что собственные значения дискретного спектра в одномерном случае невырождены.

2) E > 0 . Частица совершает инфинитное движение. Оператор Гамильтона имеет непрерывный спектр собственных значений. Квантовые состояния непрерывного спектра называют несвязанными состояниями. Частица, находящаяся в несвязанном состоянии, способна уйти на бесконечность.

В дальнейшем мы будем заниматься численным моделированием квантовых состояний только дискретного спектра. При этом необходимо пользоваться осцилляционной теоремой.

Осцилляционная теорема. Упорядочим собственные значения оператора Гамильтона в порядке возрастания, нумеруя энергию основного состояния индексом «0»: E0 , E1 , E2 , . . . , Ek , . . . . Тогда волновая функция k -го состояния ψk(x) будет иметь k узлов (то есть, пересечений с осью абсцисс). Исключения: области, в которых потенциальная функция бесконечна.

Если интересоваться только основным и низковозбужденными состояниями, то решение уравнения Шрёдингера упрощается путем преобразования потенциала на рис. (1) к виду, представленному на рис.

7

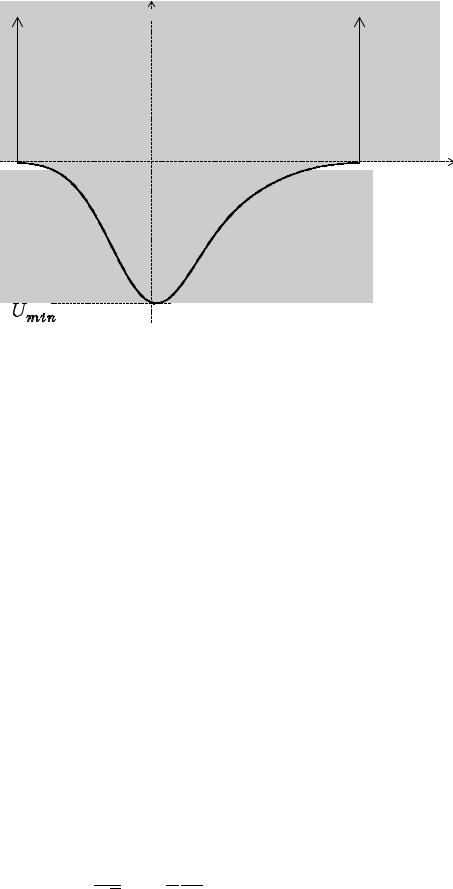
U(X)

Рис. 2. Модифицированное потенциальное поле U(x) .

(2). На этом рисунке в точках a и b по оси абсцисс построены бесконечные потенциальные стенки. Тогда волновые функции ψk(x) = 0 для x / (a, b) . Это позволяет создать сравнительно простой алгоритм. Разумеется, положения бесконечных потенциальных стенок подбираются так, чтобы численные значения актуальных энергетических уровней изменялись в допустимых пределах при сдвигах a влево, а b вправо.

Для тестирования программы необходимо использовать известные аналитические результаты. Так, можно показать, что для прямоугольной потенциальной ямы с бесконечными стенками (см. рис. (3)) собственные значения даются формулой

8

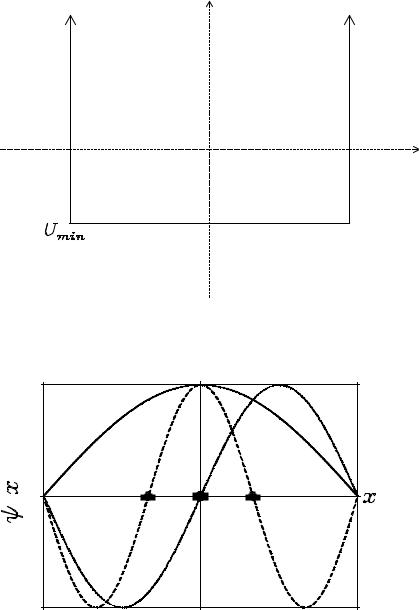
Из формулы (8) следует, что энергия основного состояния равна E1 . Волновые функции, представленные на рис. (4), хорошо иллюстрируют осцилляционную теорему.

U(X)

Рис. 3. Прямоугольная потенциальная яма с бесконечными стенками.

Рис. 4. Прямоугольная потенциальная яма с бесконечными стенками: волновые функции ψ1(x) , ψ2(x) и ψ3(x) .

9

1.1.2. Алгоритм

Как уже говорилось выше, мы будем интересоваться только основным и низко возбужденными состояниями электрона для потенциального профиля, изображенного на рис. (2). В этом случае граничные условия для волновой функции имеют очевидный вид

Для решения уравнения Шредингера удобно использовать атомные единицы (см. Приложение 1). В этих единицах уравнение (6) приобретает вид

Решение стационарного уравнения Шредингера сводится к нахождению собственных значений и собственных функций оператора Гамильтона, которые будем вычислять по изложенному ниже алгоритму..

Так как для собственных значений известна оценка снизу (4), то удобно начинать с вычисления энергии и волновой функции основного состояния. Оценим грубо энергию основного состояния. Подставим значение этой энергии в уравнение (11). Это уравнение теперь становится обыкновенным дифференциальным уравнением 2-го порядка с граничными условиями (10). Предположим, что наша оценка точно совпадает с собственным значением. Тогда, численно решая задачи Коши для полученного дифференциального уравнения интегрированием «вперед» (начальный узел сетки на левой границе) и интегрированием «назад» (начальный узел сетки на правой границе), мы должны получить для соответствующей волновой функции практически одинаковые результаты. На практике оценка собственного значения в нулевом приближении существенно отличается от точного результата. Поэтому волновые

10