Методичка по ФОКИ

функции, полученные интегрированием «вперед» и «назад», также существенно отличаются. Используя таким образом вычисленные волновые функции, можно сформулировать критерий, позволяющий уточнить собственное значение с наперед заданной точностью и, следовательно, найти для него и соответствующую волновую функцию. Рассмотрим алгоритм, реализующий эту идею.

Зададим на интервале [a, b] сетку из N узлов с постоянным шагом h = (b − a)/(N − 1) :

Граничные условия (10) приобретают вид

где использовано обозначение ψn ≡ ψ(xn) . Задачи Коши для дифференциального уравнения (11) будем решать методом Нумерова (см. Приложение 2). В рамках этого метода значение функции в узле сетки находят, используя ее значения либо в двух предшествующих узлах (интегрирование «вперед»):

ψn+1 = [2(1 − 5 c qn)ψn − (1 + c qn−1)ψn−1] (1 + c qn+1)−1, (16)

либо в двух последующих узлах (интегрирование «назад»):

ψn−1 = [2(1 − 5 c qn)ψn − (1 + c qn+1)ψn+1] (1 + c qn−1)−1, (17)

Здесь c = h2/12 , qn = q(E, xn) . При использовании формулы (16) необходимо знать ψ1 и ψ2 , а формулы (17) - ψN−1 и ψN . Значения ψ1 и ψN нам известны (15), а ψ2 и ψN−1 - нет. Однако, если N достаточно велико, то для простоты можно считать, что ψ2 = d1 , ψN−1 = d2 , где, d1 , d2 - малые числа (в силу непрерывности волновой функции). Как показывает практика, величины d1 , d2 могут варьироваться в довольно широких пределах. Заметим, что абсолютные значения этих величин не имеют принципиального значения (в разумных пределах), так как волновая функция в дальнейшем будет нормироваться.

Как уже упоминалось выше, для точного собственного значения оператора Гамильтона процедуры интегрирования «вперед» и «назад» при

11

подходящем выборе d1 , d2 должны приводить к одинаковым результатам (с точностью до постоянного множителя и ошибок округления). Также очевидно, что при неравенстве E собственному значению, эти процедуры дают различные функции, отношение которых в различных узлах сетки не равно постоянной величине. Для оценки близости E к собственному значению будем вычислять разность производных волновых функций, полученных интегрированием «вперед» и «назад», в некотором внутреннем узле сетки xm

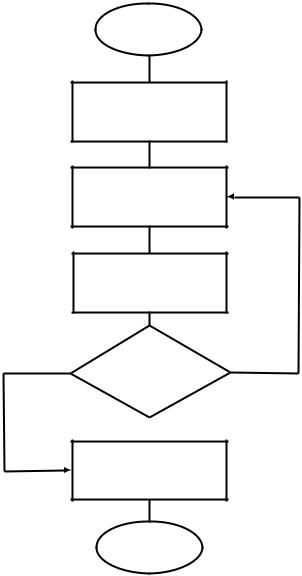
Здесь ψ> , ψ< – волновые функции, полученные интегрированием «вперед» и «назад» соответственно; xm – узел сшивки производных. Естественно, перед вычислением (18) необходимо масштабировать функции ψ> и ψ< так, чтобы ψ>(xm) = ψ<(xm) . Такое масштабирование будем называть математической нормировкой. Вычисление f позволяет организовать процедуру поиска собственного значения методом бисекции (см. блок-схему на рис. (5)). Допустим, что необходимо найти энергию и волновую функцию основного состояния. Выберем нулевое приближение к энергии основного состояния следующим образом: E(0) = Umin+δ , где δ малая величина ( δ > 0 ), и вычислим соответствующее f(0) по формуле (18). Затем будем увеличивать энергию с шагом E до тех пор, пока величины f на двух соседних шагах i и i−1 не будут иметь различные знаки. Если шаг E был меньше, чем разность энергий соседних уровней (собственных значений) в актуальном диапазоне изменения E , то можно быть уверенным, что искомое собственное значение[E(i−1), E(i)] . Далее для уточнения собственного значения с наперед заданной точностью ǫ используется метод бисекции.

Для расчета производных в формуле (18) можно воспользоваться какой-либо подходящей численной процедурой; например, по формуле

12

ВВОД

E = E(0); f (0); i = 0

i = i + 1

E(I) = E(I−1) + E

f (I) · f (I−1) < 0

МЕТОД

БИСЕКЦИИ

ВЫВОД

Рис. 5. Блок-схема процедуры поиска собственного значения.

1.1.3. Компьютерная программа

Ниже представлена программа численного решения одномерного стационарного уравнения Шредингера для электрона в прямоугольной потенциальной яме с шириной 4 а. е. длины и с бесконечными стенками; дно ямы находится на оси ординат при -1 а. е. энергии (см. рис. 3) на языке СКМ Mathematica. Сравнение полученных по этой программе данных с результатами, найденными по аналитическим формулам (8) и (9), позволяет оценить корректность алгоритма, описанного в предыдущем параграфе. Использовались атомные единицы Хартри (см.

13

Приложение 1).

1Clear["Global‘*"];

2Off[General::spell];

3 Off[General::spell1];

4L = 2.;

5 A = -L; B = +L;

6n = 161;

7 h = N[(B - A)/(n - 1)];

8c = h^2/12.;

9 Umin = -1.;

10 W = 3.;

11 U[x_Real] := If[Abs[x] < L, Umin, W];

12q[e_Real, x_Real] := 2*(e - U[x]);

13Psi = Fi = X = F = Psi2 = Table[0., {n}];

14r = (n - 1)/2 + 15;

15d1 = d2 = 10.^(-9);

16Deriv[Y_List, h_Real, m_Integer] :=

17(Y[[m - 2]] - Y[[m + 2]] +

188*(Y[[m + 1]] - Y[[m - 1]]))/(12.*h);

19Num[e_Real, d1_Real, d2_Real, r_Integer, n_Integer] := 20 Module[{i, k, big, coef, p1, p2, f1, f2, f, x},

21If[n != Length[Psi] || n != Length[Fi] ||

22n != Length[X], {Print["ERROR in Num: n=", n];

23Return[{13., Psi, Fi, X}]}];

24For[i = 1, i <= n, i = i + 1,

25X[[i]] = x = A + h*(i - 1); F[[i]] = c*q[e, N[x]]];

26Psi[[1]] = Fi[[n]] = 0.;

27Psi[[2]] = d1; Fi[[n - 1]] = d2;

28For[i = 2, i < n, i = i + 1,

29p1 = 2*(1 - 5*F[[i]])*Psi[[i]];

30 p2 = (1 + F[[i - 1]])*Psi[[i - 1]];

31 Psi[[i + 1]] = (p1 - p2)/(1 + F[[i + 1]])];

32For[i = n - 1, i > 1, i = i - 1,

33f1 = 2*(1 - 5*F[[i]])*Fi[[i]];

34f2 = (1 + F[[i + 1]])*Fi[[i + 1]];

35Fi[[i - 1]] = (f1 - f2)/(1 + F[[i - 1]])];

36p1 = Abs[Max[Psi]]; p2 = Abs[Min[Psi]];

37big = If[p1 > p2, p1, p2];

38For[i = 1, i <= n,

39i = i + 1, Psi[[i]] = Psi[[i]]/big];

14

40 coef = Psi[[r]]/Fi[[r]];

41 For[i = 1, i <= n, i = i + 1,

42Fi[[i]] = coef*Fi[[i]]];

43f = Deriv[Psi, h, r] - Deriv[Fi, h, r];

44Return[N[f]]];

45Energy = Input["Energy=?"];

46e = N[Energy];

47f = Num[e, d1, d2, r, n];

48AA = A - 1; BB = B + 1;

49Gr0 = Plot[U[z], {z, A - 0.1, B + 0.1},

50PlotStyle -> {AbsoluteThickness[2], RGBColor[0, 0, 1]}, 51 PlotRange -> {-1.1, 2.9}, DisplayFunction -> Identity];

52Point1[i_Integer] := {X[[i]], Psi[[i]]};

53H1 = Array[Point1, n];

54Style1 = {AbsoluteThickness[2], RGBColor[1, 0, 0]};

55Gr1 = ListPlot[H1, {Frame -> True, PlotStyle -> Style1,

56PlotJoined -> True}, DisplayFunction -> Identity];

57Point2[i_Integer] := {X[[i]], Fi[[i]]};

58H2 = Array[Point2, n];

59Style2 = {AbsoluteThickness[2], RGBColor[0, 0.7, 1]}; 60 Gr2 = ListPlot[H2, {Frame -> True, PlotStyle -> Style2, 61 PlotJoined -> True}, DisplayFunction -> Identity];

62Gr3 = Graphics[{RGBColor[0, 1, 0], Disk[{X[[r]], Psi[[r]]},

630.07]}, DisplayFunction -> Identity];

64Show[{Gr0, Gr1, Gr2, Gr3}, PlotRange -> {-1.1, 2.9},

65AspectRatio -> Automatic, Frame -> True,

66GridLines -> Automatic, FrameTicks -> Automatic,

67PlotLabel -> "Wave functions Psi, Fi and potential",

68FrameLabel -> {"X", "U(X),Psi(X),Fi(X)"},

69DefaultFont -> {"Arial", 14}, Background ->

70 RGBColor[1, 1, 1], DisplayFunction -> $DisplayFunction];

73ue = PaddedForm[e, {10, 9}];

74uf = PaddedForm[f, {10, 9}];

75Print[t];

76Print[t1, "e=", ue];

77Print[t1, "f=", uf];

78Print[t];

15

В первой строке программы стираются значения всех идентификаторов. Инструкции в строках 1 и 2 подавляют вывод предупреждений о наличии идентификаторов с похожими именами (следует использовать только после отладки). В строках 4 – 10 задаются численные значения ключевых параметров задачи. Идентификаторы L и Umin обозначают полуширину и минимальную энергию потенциальной ямы; n и h – количество узлов расчетной сетки и её шаг. Идентификатор W представляет собой максимальное значение энергии на графике (в расчетах не используется). В строках 11, 12 запрограммированы функции U(x) и q(E, x) . В строке 13 генерируются необходимые для реализации списки длиной n , элементы которых содержат нули. Значение идентификатора r (строка 14) содержит номер узла сшивки. В 15-строке присваиваются значения параметрам d1 и d2 , которые необходимы для при использовании метода Нумерова (формулы (16) и (17)). Обратим внимание, что d1 и d2 присвоены значения одного знака. Это необходимо при расчете квантовых состояний, имеющих чётное число узлов внутри интервала [a, b] (в том числе и основного состояния - ноль узлов). В противном случае, строго говоря, величины d1 и d2 должны иметь противоположные знаки. Функция вычисления производной в заданном узле расчетной сетки по формуле (19) находится в строках 16 – 18. Функция Num , вычисляющая для заданной энергии функции ψ>(x) , ψ<(x) в узлах сетки и f , запрограммирована в строках 19 – 44. В учебных целях в представленном листинге не используется метод бисекции, так как ввод энергии с клавиатуры (строка 45) лучше позволяет понять алгоритм решения задачи. В последующих строках программы осуществляется вывод численного значения f для введенного e (напомним, что в СКМ Mathematica по умолчанию « E » является основанием натурального логарифма), а также графики.

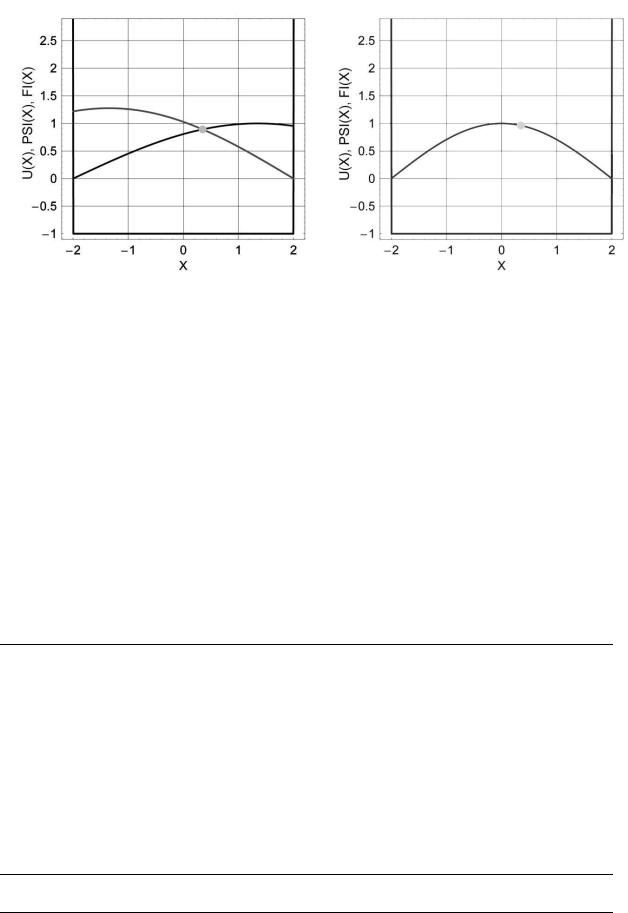
Приведем результаты работы программы для двух значений энергии. Для e = −0.89 а. е. получаем f = 0.640026056 и график, представленный на рис. 6(a). Из этого графика следует, что функции ψ>(x) и ψ<(x) очень сильно отличаются, разность производных f также весьма значительна. То есть, данное значение e весьма далеко от точного

16

Рис. 6. Волновые функции, полученные интегрированием «вперед» и «назад» для: a) e = −0.89 а. е.; b) e = −0.6915749 а. е.

собственного значения. Заметим, что на этом же графике изображена потенциальная яма. Это сделано для наглядности. Ясно, что U(x)

иволновые функции имеют различные размерности – следует иметь это в виду. Далее, при e = −0.6915749 а. е. разность производных f = 1.551988378 · 10−7 , функции ψ>(x) и ψ<(x) на рис. 6(b) сливаются. Это значение энергии вычислено по точной аналитической формуле (8)

инапечатано с 7-ю значащими цифрами после десятичной точки (напомним, что в СКМ Mathematica десятичные дроби имеют мантиссу с 15 знаками); ниже представлен соответствующий код:

1 Ek[k_Integer] := N[Umin + Pi^2*(k^2/(8*L^2))];

3tau = " E, a.u."; tev = " E, eV";

4Print[tt];

5 Print["k", " ", tau, " ", tev];

6Print[tt];

7For[k = 1, k <= 5, k = k + 1, Ea = Ek[k];

8ua = PaddedForm[Ea, {12, 7}]; Ev = 27.212*Ea;

9 uv = PaddedForm[Ev, {12, 7}]; Print[k, ua, uv]];

10 Print[tt];

Результат выполнения этого кода:

17

-----------------------------

k E, a.u. E, eV

-----------------------------

-----------------------------

Функция на рис. 6(b), согласно осцилляционной теореме, является волновой функцией основного состояния. Заметим, что прямое сравнение полученной функции с аналитической зависимостью (9) некорректно, так как не выполнена квантово-механическая нормировка, то есть, интеграл (7) не равен единице. Выполнить квантово-механическую нормировку рассчитанной волновой функции предоставляется читателю.

1.1.4. Условия задач.

Ниже предлагаются задачи по модификации и практическому использованию программы из параграфа 1.1.3.

Задача №1. Дополнить программу квантово-механической нормировкой волновых функций и выполнить сравнение вычисленных ψk(x) с аналитическими результатами (9) для основного и первых 4-х возбужденных состояний.

Задача №2. Модифицировать программу, вставив в неё процедуру уточнения собственного значения методом бисекции (см. блок-схему на рис. 5) и финальную квантово-механическую нормировку волновой функции.

Задача №3. Электрон находится в потенциальном поле U(x) = V0·v(x) , где

18

˚

V0 = 20 эВ, L = 2 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного и 1-го возбужденного состояний. Вычислить средние значения x и x2 в этих состояниях. Проверить ортогональность полученных волновых функций.

Задача №4. Электрон находится в потенциальном поле U(x) = V0·v(x) , где

˚

V0 = 10 эВ, L = 2 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного и 2-го возбужденного состояний. Вычислить, с какой вероятностью частицу можно обнаружить в этих состояниях на интервале [−L, −L/2] . Найти средние значения импульса и квадрата импульса в данных состояниях.

Задача №5. Электрон находится в потенциальном поле U(x) = V0 ·

ции для основного и 3-го возбужденного состояний, а также плотности вероятности и средние значения кинетической и потенциальной энергий для этих состояний.

Задача №6. Электрон находится в потенциальном поле U(x) = V0·v(x) ,

V0 = 5 эВ, L = 2 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного и 2-го возбужденного состояний. Используя полученные данные, проверить непосредственным вычислением справедливость соотношения неопределенностей Гейзенберга.

19

Задача №7. Электрон находится в потенциальном поле U(x) = V0·v(x) , где

˚

V0 = 1 эВ, L = 2 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного и 3-го возбужденного состояний. Найти средние значения h(Δx)2i , h(Δpx)2i и их произведения в данных состояниях.

Задача №8. Электрон находится в потенциальном поле U(x) = V0·v(x) ,

V0 = 25 эВ, L = 5 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного, 1-го и 2-го возбужденного состояний, а также средние значения импульса, кинетической энергии

˚ ˚

и вероятность обнаружения частицы в интервале [ - 0.4 A, + 0.4 A ] в этих состояниях.

Задача №9. Электрон находится в потенциальном поле U(x) = V0·v(x) , где

˚

V0 = 15 эВ, L = 2 A. Найти энергии, нормированные волновые функции и плотности вероятности для основного и 1-го возбужденного состояний. Используя волновые функции, найти средние значения кинетической энергии в этих состояниях и сравнить результаты с приближенной оценкой hT i ≈ ~2/(8ma2) , где a - линейный размер области, в которой движется частица, а m – её масса.

20