
Методичка по ФОКИ
.pdf
1.2. Сферически симметричная квантовая яма
Задача о квантовых состояниях электрона в сферически симметричном потенциале (сферически симметричной квантовой яме) является одной из важнейших тем в учебных курсах по квантовой теории. Результаты решения этой задачи широко используются не только в физике атомов, молекул и конденсированных сред, но и в таких смежных областях как физическая химия и молекулярная биология.
Типичным примером системы со сферически симметричным потенциалом является атом водорода, состоящий из электрона и протона. Так как масса протона более чем в 1800 раз превышает массу электрона, то приближенно можно полагать, что протон покоится и расположен в начале координат. Оператор Гамильтона для электрона в поле протона имеет вид
Hˆ = |
− |
~2 2 |
+ U(R), |
(20) |
|
2me |
|||||
|
|
|
где me – масса электрона. Заметим, что, так как потенциал сферически симметричен, то
U(R) = U(|R|) = U(r). |
(21) |
Потенциальное поле вида (21) называют центральным потенциалом. Решать уравнение Шрёдингера с потенциалом типа (21) удобнее в сферической системе координат. Координаты декартовой и сферической систем связаны формулами:
x = r sin θ cos φ, |
0 |
≤ r < ∞; |
|
|
0 |
φ |
2 π; |
y = r sin θ sin φ, |
|||
|
|
|
|
|
|
≤ |
≤ |
z = r cos θ, |
0 |
≤ θ ≤ π, |
|
где θ – полярный, а φ – азимутальный угол. См. рис. 7. В сферических координатах
2 = r2 |
|
∂r |
r2 ∂r |
|
ˆ |
|
|
+ r2 . |
|||||
1 |
|
∂ |
|
∂ |
|
Λ |
Здесь ˆ – оператор Лежандра:
Λ
Λˆ = |
1 |
|
∂ |
sin θ |
∂ |
|
+ |
1 ∂2 |
. |
||
sin θ |
∂θ |
∂θ |
sin θ |
|
∂φ2 |
||||||
(22)
(23)
21
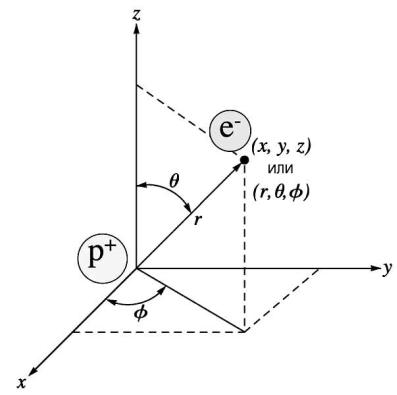
Рис. 7. Сферическая система координат.
Собственные значения и собственные функции оператора Лежандра хорошо известны
h i
ˆ (24)
Λ + ℓ(ℓ + 1) Yℓm(θ, φ) = 0,
что будет использовано нами ниже. Здесь Yℓm(θ, φ) – шаровая функция или сферическая гармоника, ℓ = 0, 1, 2, . . .; m = 0, ±1, ±2, . . . , ±ℓ ,
Yℓm(θ, φ) = Θℓm(θ)Φm(φ). |
(25) |
Аналитический вид Θℓm(θ) и Φm(φ) приведен, например, в [4]. Заметим, что оператор Лежандра с точностью до постоянного множителя совпадает с оператором квадрата момента количества движения (или
углового момента) |
ˆ |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
||
|
|
|
ˆ2 |
|
2 |
ˆ |
(26) |
|
|
|
ˆ2 |
L |
= −~ |
Λ; |
|||
|
|
|
2 |
ℓ(ℓ + 1)Yℓm(θ, φ), |
(27) |
|||
|
|
L |
Yℓm(θ, φ) = ~ |
|||||
где |
ˆ |
– оператор импульса. |
|
|||||
L = [ˆR × Pˆ] , Pˆ |
|
|||||||
|
Далее, потенциальная энергия взаимодействия электрона и протона |
|||||||
|
|
|
U(r) = − |
e2 |
(28) |
|||
|
|
|
|
. |
||||
|
|
|
r |
|||||
22
U(r) |
0 |
|
r |
|
|
|
|
|
( |
) = - |
2 / |
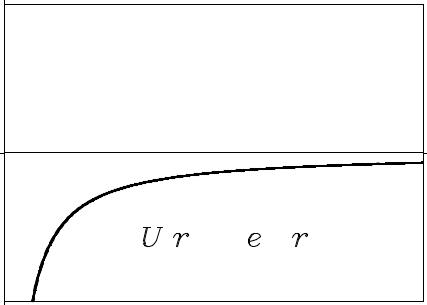
Рис. 8. Потенциальная функция взаимодействия электрона и протона.
С учетом (28) и (22), формула (20) приобретает вид
|
2 |
|
∂r |
r2 |
∂r |
− |
2 ˆ |
2 |
(29) |
|
Hˆ = −2mer2 |
|
2mer2 |
− r . |
|||||||
~ |
|
|
∂ |
|
∂ |
|
~ Λ |
|
e |
|
Волновые функции стационарных состояний ищутся в мультипликативном виде
ψEℓm(r, θ, φ) = f(r)Yℓm(θ, φ). |
(30) |
Функцию f(r) называют радиальной волновой функцией, а функцию
R(r) = r · f(r) |
(31) |
вспомогательной радиальной волновой функцией. Уравнение Шрёдингера с оператором Гамильтона (29) при учете (30),(31) и (24) приводится
к виду |
|
|
|
|
|
|
|
|
|
||
|
d2R(r) |
+ |
2meE 2mee2 |
ℓ(ℓ + 1) |
R(r) = 0. |
(32) |
|||||
|
|
|
|
+ |
|
− |
|
|
|||
|
dr2 |
~2 |
~2r |
r2 |
|||||||
Уравнение (32) называется радиальным уравнением Шрёдингера. Квантовые состояния с E < 0 отвечают области инфинитного движения (см. рис 8), то есть, дискретному спектру собственных значений. Будем рассматривать именно такие состояния. Можно показать, что собственные значения радиального уравнения Шрёдингера выражаются простой
23

аналитической формулой |
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
mee4 |
(33) |
|||||
En = − |
|
|
· |
|
|
|
, n = 1, 2, 3, . . . . |
||||
2n2 |
~2 |
|
|||||||||
Множитель m e4/~2 |
в этой формуле перепишем в виде |
|
|||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
mee4 |
|
|
e2 |
|
|
|
||||
|
|
= |
|
|
|
= Ea ≈ 27.212 (эВ), |
(34) |
||||
|
~2 |
a |
|||||||||
где |
|
|
|
~2 |
|
|
|
||||
|
|
|
|
|
˚ |
|
|||||
|
a = |
mee2 |
≈ 0.5292 (A). |
(35) |
|||||||
называется боровским радиусом. Ea и a являются единицами энергии и длины соответственно в атомной системе единиц Хартри (см. Приложение 1). В этой системе единиц формула (33) имеет особенно простой вид
1
En = −2n2 , n = 1, 2, 3, . . . . (36) Радиальные волновые функции имеют более сложный вид
fnℓ(r) = Nnℓ |
2r |
|
ℓ |
−n + ℓ + 1, 2ℓ + 2, |
2r |
exp − |
r |
, |
(37) |
|||||||||||||
|
|
F |
|
|
||||||||||||||||||
n |
n |
n |
||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
3/2 |
|
|
|
|||
|
|
|
|
1 |
|
|
(n + ℓ)! |
|
|
|
2 |
|
|
|
|
|||||||
Nnℓ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(38) |
|||||
(2ℓ + 1)! |
2n(n |
− |
ℓ |
− |
1)! |
|
|
n |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а F (n1, n2, x) – вырожденная гипергеометрическая функция. Функции (37) нормированы условием
∞ |
|
|
Z |
fnℓ2 (r)r2dr = 1. |
(39) |
0 |
|
|
Целое число nr = n−ℓ−1 равно количеству узлов радиальной волновой функции, т. е. пересечений с осью абсцисс (исключая значение r = 0 ).
Таким образом, волновая функция электрона в атоме водорода имеет вид
ψnℓm(r, θ, φ) = fnℓ(r)Yℓm(θ, φ), |
(40) |
где n – главное квантовое число, ℓ – орбитальное квантовое число, m
– азимутальное или магнитное квантовое число. Эти квантовые числа
24

могут принимать следующие значения: |
|
|
n = 1, 2, 3, . . . ; |
|
|
ℓ |
= 0, 1, 2, . . . , n − 1; |
(41) |
m |
= −ℓ, . . . , 0, . . . , +ℓ. |
|
Для обозначения состояний с данными n и ℓ часто используют буквенно-цифровую нотацию. А именно, главное квантовое число обозначается соответствующей цифрой, а орбитальное квантовое число – буквой:
ℓ (цифра) |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
ℓ (буква) |
s |
p |
d |
f |
g |
h |
|
|
|
|
|
|
|
Например, 1s обозначает состояния с n = 1 и ℓ = 0 ; 4d – состояния с n = 4 и ℓ = 2 . Квантовым числам n и ℓ соответствуют 2ℓ+1 собственных функций и одинаковыми энергиями ( 2ℓ + 1 - кратное вырождение по магнитному квантовому числу m ). Из (36), (40) и (41) следует, что имеется
n−1 |
|
X |
|
(2ℓ + 1) = 1 + 3 + 5 + . . . + (2n − 1) = n2 |
(42) |
ℓ=0
собственных значений, численно равных друг другу. Таким образом, кратность вырождения En по ℓ и m равна n2 . Волновые функции, соответствующие этим собственным значениям, естественно, различны.
Волновые функции ψnℓm(r, θ, φ) , вообще говоря, комплекснозначны. Однако, из них можно получить и вещественные волновые функции.
Для примера рассмотрим волновые функции 2p -состояний: |
|
||||||
ψ211(r, θ, φ) = Cr exp − |
r |
sin(θ) exp(+iφ); |
|
||||
2a |
|
||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
ψ |
¯(r, θ, φ) = Cr exp |
|
|
sin(θ) exp( |
iφ); |
(43) |
|
|
|
||||||
|
211 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2a |
cos(θ). |
− |
|
|||
ψ210(r, θ, φ) = √2Cr exp |
|
|
r |
|
|
||
|
|
−2a |
|
|
|
||
|
|
|
|
|
|||
Здесь m¯ ≡ −m , C – постоянный множитель. Функции (43) вырождены, то есть описываемые ими квантовые состояния имеют одну и ту же энергию. В силу линейности стационарного уравнения Шрёдингера
25

любые новые ортонормированные комбинации вырожденных волновых функций также будут собственными функциями гамильтониана, соответствующими той же энергии. Построим вещественные волновые функции 2p -состояний следующим образом:
ψpX (r, θ, φ) = |
1 |
|
|
√ |
|
Cr exp |
− |
r |
|
|
|
||||||||||||
(ψ211(r, θ, φ) + ψ211¯(r, θ, φ)) = |
2 |
· |
x; |
||||||||||||||||||||
|
|
2a |
|||||||||||||||||||||
|
|
||||||||||||||||||||||
|
√2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
||
ψpY (r, θ, φ) = |
|
|
|
(ψ211(r, θ, φ) ψ211¯(r, θ, φ)) = |
2 |
Cr exp |
|
|
|
|
|
|
|
y; |
|||||||||
|
√2i |
|
− |
|
|
|
|
|
|
|
|
−2a |
|
· |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2Cr exp |
|
r |
|
z. |
|
|
|
|
|
|
|
|
|
||||||
ψpZ (r, θ, φ) = ψ210(r, θ, φ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
− |
2a |
· |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Волновые функции связанных состояний электронов (одночастичные состояния) в изолированных атомах называются атомными орбиталями. Отметим, что рассмотрение стационарных состояний проводилось нами без учёта спина. При рассмотрении стационарных связанных состояний электрона в центральном поле с учётом спина (но при пренебрежимо малом спин-орбитальном взаимодействии и в отсутствие внешнего магнитного поля) волновая функция имеет четыре квантовых числа: n , ℓ , mℓ , ms , где mℓ – магнитное орбитальное, а ms – магнитное спиновое квантовые числа. Такие волновые функции назы-
ваются спин-орбиталями. |
|
|
|
|
|
|
||
1.3. Компьютерная программа |
|
|
|
|
||||
Радиальное уравнение Шрёдингера |
|
|
|
|
||||
d2R(r) |
+ |
2meE |
− |
2meU(r) |
− |
ℓ(ℓ + 1) |
R(r) = 0. |
(44) |
dr2 |
~2 |
~2 |
r2 |
|||||
со сферически симметричным потенциалом U(r) общего вида не имеет, вообще говоря, аналитических решений. Следовательно, уравнение (44) необходимо решать численно. Как и в случае одномерной задачи, будем искать энергии и волновые функции основного и низковозбужденных состояний приближенно, модифицируя потенциал следующим образом:
U(r) = |
U0(r), |
r |
< rmax; |
(45) |
||||
|
|
, |
r |
≥ |
r |
max |
, |
|
|
∞ |
|
|
|
|
|
||
26

где U0(r) – точная потенциальная функция. Идеология алгоритма аналогична рассмотренной ранее (см. параграф 1.1.2). Для тестирования компьютерной программы решения уравнения (44) разумно воспользоваться известными частными результатами для кулоновского потенциала – формулами для энергий и волновых функций стационарных связанных состояний атома водорода. Написать такую программу и выполнить её тестирование предоставляется читателю. Чтобы облегчит эту задачу, ниже приведен код, который для известного значения энергии электрона основного состояния в атоме водорода позволяет численно рассчитать нормированную вспомогательную радиальную волновую функцию с использованием потенциала вида (45). Используется атомная система единиц Хартри. В отличие от программы, приведенной в параграфе 1.1.3, задача Коши решается с помощью встроенной функции ядра СКМ Mathematica. Во избежание возможных проблем с кириллическими надписями, текст на русском языке приводится только в комментариях.
1Clear["Global‘*"];
2Off[General::spell];
3Off[General::spell1];
4 |
n=1; |
(* главное квантовое число |
*) |
5 |
l=0; |
(* орбитальное квантовое число *) |
|
6 |
e=-1/(2*n^2); |
(* энергия электрона |
*) |
7rmin=0.001;
8rmax=40.;
9 {{res}}=NDSolve[{R’’[r]+(2*e+2/r-l*(l+1)/r^2)*R[r]==0,
10 R’[rmax]==-1,R[rmax]==0},R[r],{r,rmin,rmax}];
11 s=NIntegrate[(R[r]/.res)^2,{r,rmin,rmax}];
12qnorm=1/Sqrt[Abs[s]];
13Print["qnorm=",qnorm];
14R1s[r_Real]:=N[(2*r)*Exp[-r]];
15f1=PaddedForm[qnorm*R[r]/.res,{10,7}];
16f2=PaddedForm[R1s[r],{10,7}];
17t="-----------------------------------------";
18Print[t];
19 |
Print[" r |
Numerical |
Analytical"]; |
20 |
Print[t]; |
|
|
21 |
For[r=rmin,r<=4,r=r+0.5, |
|
|
27

22Print[PaddedForm[r]," ",f1," ",f2]];
23Print[t];
24s1=NIntegrate[R1s[r]^2,{r,rmin,rmax}];
25(* test for R1s *)
26Print[" Normalizing for analitical R1s: ",s1];
27ps1={{Thickness[0.009],RGBColor[1,0,0]}};
28as1={AbsoluteThickness[1],RGBColor[0,0,1]};
29al1={"r, a.u.","R1s(r)"};
30 name="Numerical result for R1s(r)";
31 df={"Arial-Oblique-Bold",12};
32Plot[qnorm*(R[r]/.res),{r,rmin,rmax/4},
33PlotStyle->ps1,AxesStyle->as1,AxesLabel->al1,
34GridLines->Automatic,PlotLabel->name,DefaultFont->df,
35AspectRatio->1,Background->CMYKColor[0,0.1,0.1,0]];
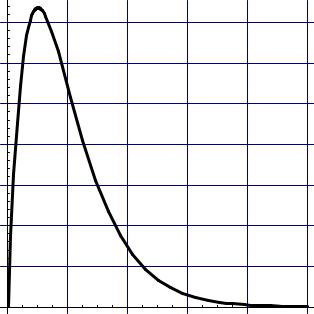
Программа проста и не заслуживает каких-либо пояснений. Результаты выполнения этого кода: таблица (приведена ниже) и рис. 9.
qnorm = 6.62519 10^{-16}
-------------------------------
r Numerical Analytical
-------------------------------
0.001 |
0.0019980 |
0.0019980 |
0.501 |
0.6071363 |
0.6071363 |
1.001 |
0.7357585 |
0.7357585 |
1.501 |
0.6691672 |
0.6691672 |
2.001 |
0.5410705 |
0.5410705 |
2.501 |
0.4101788 |
0.4101788 |
3.001 |
0.2985233 |
0.2985233 |
3.501 |
0.2112308 |
0.2112307 |
-------------------------------
1.3.1. Условия задач.
Задача №1. С помощью СКМ Mathematica получить аналитические формулы для радиальных и угловых частей волновых функций электрона в атоме водорода 1s -, 2s -, 3s -, 2p -, 3p -, 4p -, 3d -, 4d -, 5d - состояний путем упрощения формул (38) и (25).
28
R1SHR L |
NUMERICAL RESULT FOR R1SHR L |
|
|||
0.7 |
|
|
|
|
|
0.6 |
|
|
|
|
|
0.5 |
|
|
|
|
|
0.4 |
|
|
|
|
|
0.3 |
|
|
|
|
|
0.2 |
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
R , A.U. |
|
2 |
4 |
6 |
8 |
10 |
|
Рис. 9. Функция R1s(r) . |
|
|||
Указание: использовать библиотечные функции ядра СКМ Mathematica для вырожденной гипергеометрической и шаровой функций.
Задача №2. Построить графики радиальных волновых функций элек-
трона в атоме водорода 1s -, 2s -, 3s -, 2p -, |
3p -, 4p -, 3d -, 4d -, |
5d - состояний. Убедиться, что они имеют nr |
= n − ℓ − 1 узлов для |
r (0, ∞] . |
|
Указание: использовать результаты предыдущей задачи.
Задача №3. Построить графики радиальной части плотности вероят-
ности Dnℓ(r) = 4πr2fnℓ2 (r) в 1s - и 2s - состояниях для r [0, 8] ( r
– в атомных единицах ). Определить, при каких r радиальная часть плотности вероятности имеет максимумы и минимумы.
Задача №4. Построить полярные диаграммы угловых частей волновых функций 2px , 2py , 2pz и проанализировать полученные изображения. Указание: для построения полярной диаграммы на радиусах-векторах, отвечающих всем возможным значениям углов, отложить модуль угловой части волновой функции для соответствующих θ и φ . Полученная
29
поверхность и есть полярная диаграмма. Построить трехмерные графики или/и проекции полярных диаграмм на плоскости XY, XZ и YZ. Использовать встроенные функции СКМ Mathematica ParametricPlot3D или/и ParametricPlot.
Задача №5. Написать программу для численного решения радиального уравнения со сферически симметричным потенциалом произвольного вида (44). Для тестирования использовать результаты для кулоновского потенциала (28). Вывести таблицы и графики. Выполнить сравнение с аналитическими результатами.
30
