
Парадокс Бертрана
В некоторых задачах по теории вероятности требуется геометрический подход (например, попадание пуль в мишень). В задачах такого типа предполагается, что случайные точки равномерно распределены в некоторой области. Вероятность попадания в произвольную часть этой области пропорциональна ее площади (длине или объему). Такие вероятности приводят к возникновению ряда парадоксов. Например, шанс попасть в центр мишени ( или в любую другую заданную точку) равен нулю. С другой стороны, попасть в эту точку можно. Таким образом, необходимо различать невозможные события и события, происходящие с вероятностью 0 (вероятность невозможного события равна 0, но обратное неверно). Может показаться странным следующий факт: вероятность попадания по крайней мере в одну точку из конечного множества точек и вероятность попадания лишь в одну точку совпадают (обе вероятности равны 0. см. парадокс о нулевой вероятности). Другая странность: взаимно однозначное преобразование может совершенно изменить шансы. Например, если мы случайно выбираем точку из интервала (0, 1), то шансы выбрать число меньшее 1/2, равны 50%. Но если все числа из (0,1) возвести в квадрат и равномерно выбирать из квадратов, то шансы увеличатся до 65,6%. Конечно, ответ 50% более естественен, но в других задачах выбор между естественностью и неестественностью может оказаться невозможным только на основе логических рассуждений.
Суть парадокса
Для некоторой окружности случайным образом выбирается хорда. Найти вероятность того, что эта хорда длиннее стороны правильного треугольника, вписанного в окружность. Парадокс утверждает, что такая вероятность определяется неоднозначно, т.е. различные методы приводят к разным результатам.
|
1-ый
метод
С |
|
2-й
метод
И |
|
3-й
метод
В |
Объяснение парадокса
Казалось бы, во всех трех случаях рассуждения верны, но все-таки вероятность одного и того же события оказалась разной. Однако на самом деле мы решали три различные задачи (т.е. за меру выбирались различные множества).
В первом случае за меру множества точек избрали площадь, в которой эти точки расположены, и вычисляли отношение двух площадей.
Во втором случае за меру множества точек, попадающих в определенный угол, приняли величину соответствующего угла и вычисляли отношение двух углов(т. е. угла π/3 и развернутого угла π).
Ну а в третьем случае мы "катили" хорду по диаметру и, принимая длину отрезка за меру множества точек на нем, вычисляли отношение длины отрезков.
8 ученик Парадокс 4

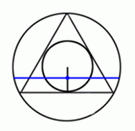 лучайным
образом (равномерно) в круге выбирается
точка. Эта случайная точка определяет
единственную хорду, серединой которой
она является. Эта хорда длиннее стороны
вписанного правильного треугольника
тогда и только тогда, когда ее середина
лежит внутри круга, вписанного в
треугольник. Радиус этого круга равен
половине радиуса исходного круга,
следовательно площадь вписанного
круга составляет 1/4 площади исходного.
Таким образом, вероятность того, что
случайно выбранная точка лежит внутри
вписанного круга, равна 1/4.
лучайным
образом (равномерно) в круге выбирается
точка. Эта случайная точка определяет
единственную хорду, серединой которой
она является. Эта хорда длиннее стороны
вписанного правильного треугольника
тогда и только тогда, когда ее середина
лежит внутри круга, вписанного в
треугольник. Радиус этого круга равен
половине радиуса исходного круга,
следовательно площадь вписанного
круга составляет 1/4 площади исходного.
Таким образом, вероятность того, что
случайно выбранная точка лежит внутри
вписанного круга, равна 1/4.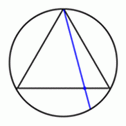 з
соображений симметрии можно считать,
что одним концом хорды является
произвольная фиксированная точка на
окружности. Пусть этой точкой является
вершина вписанного треугольника.
Выберем другой конец случайно с
равномерным распределением. Вершины
треугольника делят окружность на три
равные дуги, и случайная хорда длиннее
стороны правильного треугольника,
если она пресекает этот треугольник.
Так что искомая вероятность теперь
равна 1/3.
з
соображений симметрии можно считать,
что одним концом хорды является
произвольная фиксированная точка на
окружности. Пусть этой точкой является
вершина вписанного треугольника.
Выберем другой конец случайно с
равномерным распределением. Вершины
треугольника делят окружность на три
равные дуги, и случайная хорда длиннее
стороны правильного треугольника,
если она пресекает этот треугольник.
Так что искомая вероятность теперь
равна 1/3.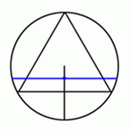 ыберем
случайным образом и равномерно точку
на радиусе окружности и возьмем хорду,
которая перпендикулярна этому радиусу
и проходит через выбранную точку.
Тогда случайная хорда длиннее стороны
вписанного правильного треугольника,
если случайная точка лежит на той
половине радиуса, которая ближе к
центру. Из соображений симметрии не
важно, какой радиус был выбран для
построения, поэтому искомая вероятность
равна 1/2.
ыберем
случайным образом и равномерно точку
на радиусе окружности и возьмем хорду,
которая перпендикулярна этому радиусу
и проходит через выбранную точку.
Тогда случайная хорда длиннее стороны
вписанного правильного треугольника,
если случайная точка лежит на той
половине радиуса, которая ближе к
центру. Из соображений симметрии не
важно, какой радиус был выбран для
построения, поэтому искомая вероятность
равна 1/2.